建设项目多目标调度优化的粒子群算法

刘新博，刘晓伟，郭 诚，张 巍

建设项目多目标调度优化的粒子群算法

刘新博1，刘晓伟1，郭 诚2，张 巍3

（1.辽宁工业大学 管理学院，辽宁 锦州 121001; 2. 国网锦州供电公司，辽宁 锦州 121000; 3. 辽宁广播电视大学 锦州分校，辽宁 锦州 121000）

考虑建设项目多目标调度优化问题，将最小化工期和资源均衡作为优化目标，通过有向无环图表述一项具体工程项目，进而结合资源约束构造问题的数学模型。基于问题的NP难解性，设计粒子群算法以优化施工方案。通过定义粒子编码方式、设计运算符重载策略、设置算法运行参数、设定初始化及停止准则以完成算法整体流程设计。以某公司建设项目为实例，验证表明，该算法能够有效地解决文中所考虑的问题，可以为施工者在制定施工方案过程中提供有效的策略支持。

项目调度；最小化工期；资源均衡；粒子群算法

为了保证建设项目高质量、低成本、短工期、重安全地完成，良好的施工组织设计尤为重要[1]。其中，进度控制作为施工组织设计中不可忽略的一个重要环节，影响到施工过程能否被合理地调度、所需资源能否被均衡地利用、施工团队能否被合理地组织，等等，从而决定了能否优质、高效、低耗地达到施工目的，以满足企业和社会的需求[2]。

随着信息科技的发展，利用计算机技术对建设项目的施工方案进行分析设计，从而达到项目资源调度、施工组织优化的目的，已成为工程管理领域的研究热点之一[3]。一方面，研究人员将数学建模、算法设计等技术融入到项目调度的理论模型之上，丰富了理论层面的研究成果；另一方面，将这些理论结果应用到实际工程之中，很好地指导了实际工程建设项目的施工过程。例如：Kellenbrink和Helber[4]考虑了资源受限且活动间含有先后序约束关系的项目调度问题，设计了一个遗传算法对问题进行求解；Elbeltagi等[5]人研究了考虑施工工期、建设成本等多个目标的施工进度优化问题，为该问题设计了一个基于帕累托前沿折衷进化策略的粒子群优化算法进行求解；Chakrabortty等[6]人考虑了具有已知确定性可再生资源、但活动持续时间具有随机性的资源受限的项目调度问题，提出了一种基于鲁棒优化的方法；近期Kadri和Boctor[7]考虑了带有传输时间的资源受限项目调度问题，他们研究了非抢占模式、且任务之间先后序关系是零滞后的情况，为其设计了一种使用两点交叉算子的改进遗传算法；Habibi等[8]人考虑了项目实施成本和项目费用之间的权衡与关联，设计了两个多目标元启发式算法（多目标遗传算法和多目标粒子群算法）进行求解。最后，将所得方案应用于伊朗铁路建设项目之中，获得了很好的施工效果。

本文针对建设项目常见的模型——带资源约束的多目标项目调度（resource constrained multi-objective project Scheduling，RCMPS）问题，设计了一个基于粒子群算法的施工优化方案。论文主要结构为：第二部分介绍了带资源约束的多目标项目调度问题，并通过数学模型对其进行形式化表述；第三部分为问题设计了一个多目标粒子群优化算法（Particle Swarm Optimization，PSO）；第四部分以某公司建设项目的某项子工程为实例，证实PSO算法可以有效地求解RCMPS问题，为施工者提供合理决策；最后总结并指出未来的研究方向。

1 问题介绍及建模

实际工程中需要考虑的优化目标是多方面的，如工期最短、成本最低、资源均衡等等。然而，上述几个目标往往是相互矛盾的，也就是说，任何一种施工方案均无法同时使得这些目标达到最优，这就需要对各个目标之间进行取舍，选择较为合理的一种施工方案。

利用计算机技术优化施工方案的过程中，一项具体工程往往可以通过一个有向无环图（Directed acyclic graph，DAG）= (,)来表示。其中为图的节点集合，表示该工程各道工序的开始或结束事件。为的边集合，表示需要消耗一定施工时间的某个环节（即工序）；若有边E∈（即VV），则说明工程中具有一道工序(,)（在不影响理解的前提下，用E表示这道工序），其开始事件为V，结束事件为V；同时，V和V也可能是其他工序的开始或结束事件，通过这种形式就能够表示工序之间的先后序约束关系。一个DAG实例如图1所示。

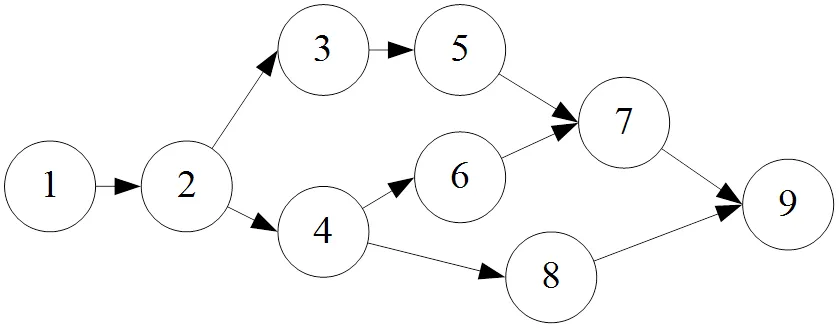
图1 DAG实例

若用图1中的DAG图表示一个工程项目，则该项目包括1~9等9个事件，其中1号事件（1）代表工程的开始、9号事件（9）代表工程的结束；此外，该工程具有12、23、24等10道工序，以24为例，其前序工序为12、后继工序为46和48。此外，为了形式化地表述文中考虑的问题，介绍其他符号如表1所示。

表1 相关符号

本文考虑的施工优化目标为两个：最小化工期与资源使用均衡。其中前者很容易理解，因为施工甲乙双方都希望在满足施工质量的前提下，项目的工期越短越好；而后者主要指的是施工过程中各种资源的使用应该尽量保持均衡，避免出现过多资源紧张或闲置的情况，本文使用最小方差法作为资源均衡的度量标准。

基于上述分析，构造本文所研究问题RCMPS的数学模型如下：

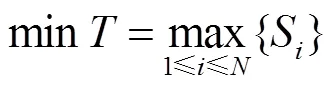
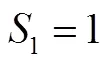
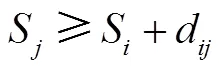
≤（5）

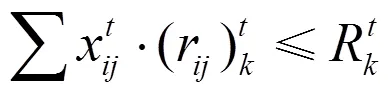
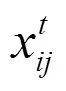
2 粒子群优化算法

最简单的平行机调度问题已经是NP难问题，而本文所考虑的RCMPS问题是其更为复杂的情况，因此也无疑是NP难的。对于该问题，本文设计了一个粒子群算法（particle swarm optimization，PSO）对其进行求解。

2.1 算法通用框架

粒子群（PSO）算法模仿了自然界生物群体如鸟群、鱼群的觅食过程，是一类由种族智慧启发而来的基于种群的随机搜索启发式算法[9]，被广泛地应用在求解项目调度、路径规划等优化问题。

在PSO算法的通用框架中，整体种群包含个粒子，每个粒子将表达所求解问题的一个候选解。粒子具有其位置x（表达一种可行方案）和速度v（表达其更新趋势），算法的优化过程就是利用了这些粒子之间的相互作用，即粒子所找到的“最优位置”将会影响其他粒子的运动方向，使得种群中每个粒子均通过两个因素持续调整自己的位置以靠近全局最优（粒子自身访问过的最佳位置pbest和整个种群访问过的最佳位置）。对于粒子而言，其速度和位置的更新方式为：

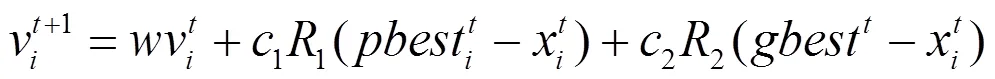
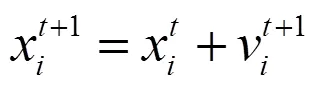
其中，各个参数的上标表示算法迭代的轮次；为权重系数，反映了上一代速度对本轮更新的影响；1和2为学习因子，反应局部最优解和全局最优解对本轮更新的影响；1和2为保证搜索随机性的随机变量。使用PSO算法求解某一具体优化问题（如本文的RCMPS问题）时，需要定义粒子位置x和速度v的编码方式，重载式（8）、（9）中的减法、乘法、加法等运算操作，以及定义算法的停止准则，在完成若干轮迭代之后，算法输出运算过程中找到的最好解。

2.2 求解RCMPS问题的PSO算法

2.2.1 粒子编码方式

在PSO中，粒子的位置信息表示所求解问题的可行解，就本文所研究的RCMPS问题而言，粒子的位置x是其一个可行的施工方案。本文用一个||×矩阵作为粒子位置信息的编码方案，其中||是图中边的数量（即工程中工序的数量），为施工甲方所规定的最长工期；矩阵中的元素为0或1，表示当前工序在第天是否有施工行为。采用这种编码方式的优势在于，其可以快速直接地转换成项目施工所对应的甘特图，图1中DAG所对应的一个有效位置编码（即施工方案）如图2所示。

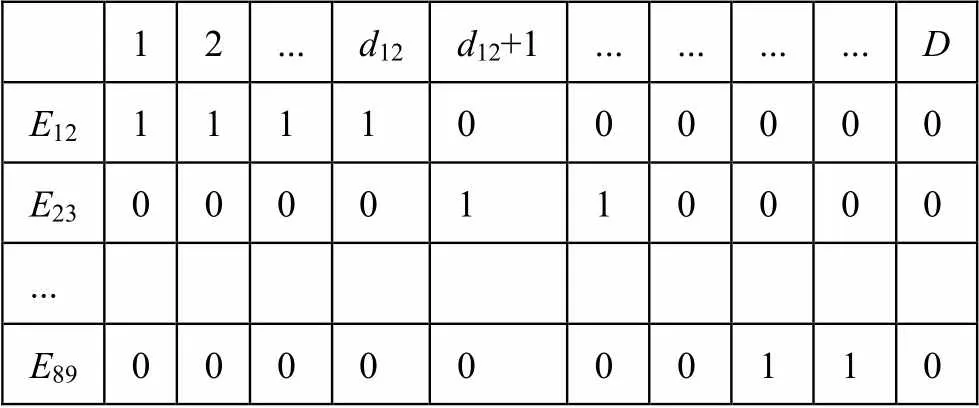
12...d12d12+1............D E121111000000 E230000110000 ... E890000000110

在本文考虑的问题中，工序E的施工时间为输入常数d，因此，在E所对应行向量中，取值为1的元素共有d个。此外，根据工序之前的先后续关系，E所对应的行向量中第一个取值为1的元素，不得早于E所对应的行向量中最后一个取值为1的元素（1≤,,≤）。

粒子的速度v用于与其位置x做加法运算，以便在PSO迭代的过程中更新位置的编码。本文中，粒子的速度采用与位置相同的编码形式，即通过一个||×矩阵为粒子速度进行编码；矩阵内元素的取值范围也在{0, 1}选择，具体计算方法将在2.2.2中介绍。

2.2.2 运算符重载

公式（8）和（9）中的减法、乘法、加法运算是保证粒子位置更新的基本操作，针对问题特性，需要对这些运算符进行重载。重载方案既要保证编码的可用性、又要保证更新的有效性，也就是说，粒子的更新应该向其局部最优和全局最优方向靠拢，且新生成的编码依然是一种有效的调度方式。

（1）减法运算。用于计算当前位置距离局部最优或全局最优的“差距”，根据这些差距来计算/调整粒子下一步的运动方向。由公式（8）可知，参与减法计算的被减数（用表示）和减数（用表示）均为粒子的某一位置编码（即一个||×矩阵），定义它们的差（用表示）依然为一个||×矩阵，其(,)位置上的元素为、对应位置元素之差的绝对值，即：若=-，则c= |a-b|, 其中,a∈,b∈,c∈且1≤≤||, 1≤≤。

（2）乘法运算。作用于随机变量（1和2）与减法所得的差值之间，表示对减法操作结果的一次随机重定位。本文PSO中1和2的结构与粒子位置编码方式相同，即元素为0或1的随机||×矩阵。因此对于乘法运算=×，其结果为:

其中，1≤≤||，1≤≤。

算法1 PSO中的加法操作

输入： 加数、（均为||×矩阵）

输出：、之和（依然为||×矩阵）

步骤1：对于矩阵中的每一行向量C（1≤≤||），记其所对应的施工工序为E，做步骤2~5：

步骤2： for each 1≤≤

步骤3：c=a+b；\对应位置加和

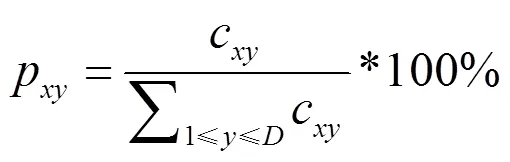
步骤5：依据概率p，从C中选择d个元素将其值置为1；其余元素置为0；

步骤6：重复步骤2~5直至遍历中的所有行向量；

步骤7：若出现工序之间违背先后序约束的情况，则后继工序向后顺延。

2.2.3 参数设置及算法流程

本文PSO算法构造种群大小为30，即种群中共有30个粒子进行迭代，采用随机形式生成初始编码；定义算法停止准则为迭代500次，即当迭代轮次大于500时，算法停止；设置权重系数、学习因子1、2均为1，随机变量1和2为随机生成的{0, 1}矩阵（大小为||×）。由于文中考虑的RCMPS问题为双目标问题，因此50%的粒子以最小化工期为主目标、以资源均衡为次目标，另外50%的粒子恰好相反。综上，本文PSO算法的整体流程如算法2所示。

算法2 求解RCMPS问题的PSO算法

输入： 图= (,)（描述某一工程的DAG图）；输出：遍历过程中找到的最优施工方案（可能不止1个）。

步骤1：生成30个粒子，按照2.2.1中的编码方式随机初始化；

步骤2：设置迭代轮次变量= 1；

步骤3：(≤500)

步骤4：根据式（8）、（9）和2.2.2中的运算符重载规则对种群进行更新；

步骤5：++；

步骤6：输出遍历过程中找到的最优施工方案（可能不止1个）。

3 实例分析

3.1 实例描述

本节通过具体实例验证所设计的PSO算法的有效性，说明其可以在施工前期辅助管理者制定合理的施工方案。事实上，图1中的DAG来自于某公司正在实施的建设项目中的某项子工程，表示了厂房施工过程中的土建工程施工、钢结构主体工程施工、传动系统施工、机电安装工程施工、覆盖系统施工、整体测试等各项工序；工程所需资源包括人力资源以及砼振捣器、搅拌机等施工设备。项目抽象化后的参数如表2所示。

表2 实例参数

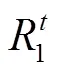
3.2 PSO运算结果

在未使用PSO的情况下，通过传统的网络工程计划方法（如双代号网络图），可得实例的施工甘特图如图3所示。然而，图3中的施工方案未考虑资源约束，也没有考虑资源均衡这一优化目标，所以并不符合实际的项目需求（不可行方案）。

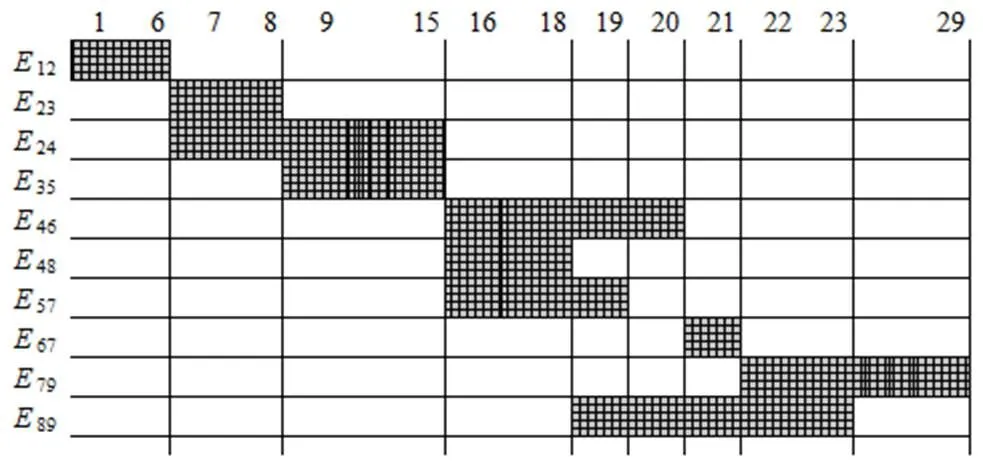
图3 未考虑资源约束和资源均衡的施工方案

而PSO算法给出的施工方案如图4所示。可以发现，由于资源约束的存在，图4方案比图3方案的工期要多5天（34天），但是图4方案是可行的，且在此基础追求工期最小化。另外，计算可得图4方案所对应的资源均衡度为=4.0447。事实上，可以通过延长工期以缩小资源均衡度（意味着人力、设备、保障等资源分配的更加均匀），PSO算法会生成多组可行方案，供施工管理者选择。最后，PSO算法的运行时间在5 s左右，完全符合计算需要。

图4 PSO算法给出的施工方案

4 结论

本文考虑了带资源约束的建设项目施工调度中的多目标优化（RCMPS）问题，将最小化工期和资源均衡作为施工的优化目标。首先构建了能够描述问题的数学模型，进而设计了一个粒子群（PSO）算法对其进行求解。粒子的位置和速度信息均采用矩阵形式表现，可以方便进行编、解码操作；根据问题特性重载了通用框架中的减法、乘法、加法运算，从而保证算法迭代的有效性。运算实例表明，PSO算法可以作为求解RCMPS问题的有效方法。

未来工作可以从3个方面开展：（1）虽然本文算法可以有效求解RCMPS问题，但由于其编码往往形成稀疏矩阵，可能造成计算空间的浪费；因此，更适合的编码方式可以作为未来研究内容之一。（2）PSO算法运算过程中可能陷入局部最优，因此，可以设置一定机制扩展其在搜索空间的寻优范围。（3）对于小规模问题实例，可以尝试为其设计精确算法，在可接受的时间范围内求其精确解。

[1] 曹吉鸣. 工程施工管理学[M]. 北京: 中国建筑工业出版社, 2015.

[2] 徐运明, 邓宗国. 建筑施工组织设计[M]. 北京: 北京大学出版社, 2019.

[3] Pellerin R, Perrier N, Berthaut F. A survey of hybrid metaheuristics for the resource-constrained project scheduling problem[J]. European Journal of Operational Research, 2020, 280(2): 395-416.

[4] Kellenbrink C, Helber S. Scheduling resource-constrained projects with a flexible project structure[J]. European Journal of Operational Research, 2015, 246(2): 379-391.

[5] Elbeltagi E, Ammar M, Sanad H, et al. Overall multiobjective optimization of construction projects scheduling using particle swarm[J]. Engineering, Construction and Architectural Management, 2016, 23(3): 265-282.

[6] Chakrabortty R K, Sarker R A, Essam D L. Resource constrained project scheduling with uncertain activity durations[J]. Computers & Industrial Engineering, 2017, 112: 537-550.

[7] Kadri R L, Boctor F F. An efficient genetic algorithm to solve the resource-constrained project scheduling problem with transfer times: The single mode case[J]. European Journal of Operational Research, 2018, 265(2): 454-462.

[8] Habibi F, Barzinpour F, Sadjadi S J. A mathematical model for project scheduling and material ordering problem with sustainability considerations: A case study in Iran[J]. Computers & Industrial Engineering, 2019, 128: 690-710.

[9] Kennedy J, Eberhart R. Particle swarm optimization[C]. Proceedings of IEEE International Conference on Neural Networks,1995,4: 1942-1948.

Particle Swarm Optimization for Construction Project Scheduling with Multi Criteria

LIU Xin-bo1, LIU Xiao-wei1, GUO Cheng2, ZHANG Wei3

（1. School of Management, Liaoning University of Technology, Jinzhou 121001, China;2. State Grid Jinzhou Electronic Power Supply Company, Jinzhou 121000, China;3. Jinzhou Branch of Liaoning Radio and TV University, Jinzhou 121000, China）

Considering a multi-objective scheduling problem for construction projects with the goals of minimizing the makespan and balancing the project resources, a specific construction project is presented by a directed acyclic graph, and then the mathematical model is constructed considering the resource constraints. Since the NP problem is hard to solve, a particle swarm optimization approach is proposed to form a construction plan. By particle encoding, operators overloading, parameters tuning, as well as initialization and termination criteria setting, the completed design of the algorithm is given. Finally, an actual construction project is taken as the example, and the experiments show that the method can solve the considered problem effectively, which can provide some reasonable strategies for the managers in a construction project.

project scheduling; minimizing makespan; resource balance; particle swarm optimization

F224

A

1674-3261(2021)01-0063-05

2020-02-20

刘新博(1982-)，女，辽宁锦州人，硕士生。

刘晓伟(1964-)，男，辽宁锦州人，教授，硕士。

责任编校：刘亚兵