基于灵敏度排序的焊点布置鲁棒性分析方法研究*
2021-01-13宋海生陈志勇杨昌海史文库
宋海生,陈志勇,杨 娜,杨昌海,史文库
(1. 吉林大学,汽车仿真与控制国家重点实验室,长春 130022;2. 一汽—大众汽车有限公司技术开发部,长春 130022 )
前言
电阻点焊(RSW)是汽车工业主要采用的制造技术,典型轿车白车身往往具有3 000 ~5 000 个焊点。在整车寿命中,制造不精确、小的事故和疲劳失效都可能导致大量的焊点连接的劣化或脱落[1-5]。焊点的鲁棒性就是指焊点布置方案对于制造过程中的不确定性(焊点的位置变化、焊点的漏焊和焊点的失效等)和由于汽车整个使用寿命中的疲劳效应导致的焊点破坏的抗干扰性。一个优良的方案应该具有较强的鲁棒性,即不应该因为某一个或几个焊点的失效而使整个方案的效果大打折扣[6-7]。
目前,鲁棒性分析主要采用蒙特卡洛仿真方法(MC),其存在以下缺点[8-15]:①成本高效率低,每次仿真都需要大量的抽样,这意味着需要大量的性能仿真计算;②精度严重依赖抽样数量,要想得到较高的精度就必须提高抽样的数量,且样本容量越大需要的抽样数量就越多。以上缺点严重制约了该方法在汽车白车身焊点鲁棒性分析中的应用,所以寻找一种高效、低成本的鲁棒性分析方法就显得尤为重要。
鉴于此,本文中提出了一种基于焊点灵敏度排序的鲁棒性分析方法。首先针对某国产轻型客车的焊点布置方案,建立了有限元模型并进行了试验验证;其次以白车身动刚度和静刚度作为性能目标,采用焊点及其相邻单元应变能对焊点进行了灵敏度的排序;然后基于上述结果提出了一种基于灵敏度排序的焊点鲁棒性分析方法,并与传统的蒙特卡洛仿真进行了对比验证,结果表明本文提出的方法具有高效、低成本的特点,仅需要较少的抽样即可获得较高的计算精度。
1 蒙特卡洛鲁棒性分析方法(MC)
鲁棒性所讨论的问题之一就是随机事件的概率计算问题,一般最常用的方法是蒙特卡洛仿真方法,主要包括一般抽样方法和重要抽样方法[16-18]。
1.1 一般抽样方法
假设存在n个随机变量,其概率密度函数分别为f(x1),f(x2),…,f(xn) ,结构性能函数表示为

则性能失效的概率可以表示为
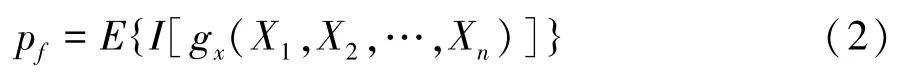
式中I[gx(X1,X2,…,Xn)] 为示性函数。对随机样本进行抽样可以得到一个样本向量由此可得性能失效概率的估计值为

由式(3)估计的失效概率的平均值为

由式(3)估计的失效概率的方差为

相应的变异系数(即模拟的精度)为

当规定了要求的模拟精度(即变异系数)后,由式(8)近似估计需要的模拟次数:

式(7)和式(8)表示了模拟精度与模拟次数之间的关系,为了达到变异系数的模拟精度,需要进行的模拟次数为N=105~107,这也是传统的蒙特卡洛效率低、成本高的原因。
1.2 重要抽样方法
为了减少蒙特卡洛模拟所需要的次数,重要抽样方法被提出。两者之间的差别如图1 所示。
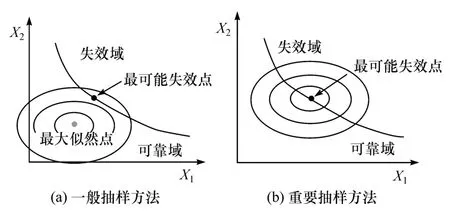
图1 一般抽样方法与重要抽样方法对比
图中同心椭圆表示联合概率密度函数的等值曲线,圆心即为联合概率密度函数的最大值点,也就是最大似然点,该点一般在随机变量的中值处或是平均值附近。当按照一般抽样方法进行随机变量的抽样时,样本点落在最大似然点处的概率最大,所以抽取的样本点大部分都落在了该点的附近。而按照性能设计的要求,性能失效是一个小概率的事件,也就是说设计性能时要使得最大似然点在可靠域内,且远离失效边界。在这种情况下,只有少数或是极少数(取决于性能失效概率的大小)的样本点落在了失效域内,落在失效域内的样本点越少,失效概率估计值的不确定性越大,鲁棒性就越差,从而估计精度越低。
所谓重要抽样方法就是通过改变抽样中心的位置或者用新的概率分布对随机变量进行抽样,来估计失效概率的值,从而达到减小变异系数的目的。
为了达到这一目的,就需要从两个方面进行考虑:一是增大样本点落入失效域的机会;二是使示性函数具有较大的权重。一个简单的方法是直接将重要抽样随机变量的中心(即平均值)选在对失效概率影响最大的点,该点可以通过如下的优化方法确定:
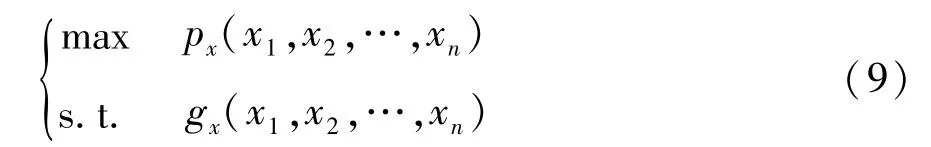
同时,也可采用一次2 阶矩方法分析得到该点的位置。以上方法在理论上虽然可以提高效率、降低成本,但这需要额外进行优化计算或是一次2 阶矩的计算,当样本数量较大时,采用上述两种方法确定最大可能失效点的工作量依然是巨大的。
2 基于焊点灵敏度排序的鲁棒性分析方法
为了克服传统鲁棒性分析方法成本高、效率低的缺点,本文中借鉴了重要抽样方法的理论,引入了焊点灵敏度排序的方法寻找最大可能失效点,相对于优化计算或一次2 阶矩计算,该方法成本低、效率高。
具有较高灵敏度值的焊点相对于具有较低灵敏度值的焊点对白车身性能具有更大的影响,这也就意味着具有较高灵敏度值的焊点落入白车身性能失效域的概率将远大于具有较低灵敏度值的焊点。本文中利用这一结论,选择具有较高灵敏度值的焊点使其失效,则会大大增加样本点落入失效域的机会,从而提高鲁棒性分析的效率。
2.1 焊点灵敏度评价方法
当白车身受到载荷作用(包括动载荷和静载荷)时会产生一定的变形,此时白车身上的每一个部件(包括焊点)都将储存一定的应变能,应变能高的区域其负载大、变形大,因此对于车身刚度影响也就较大,即所谓的高灵敏度区域。为了对白车身焊点灵敏度进行排序,本文中采用基于焊点及其相邻单元应变能的方法作为灵敏度排序的依据。其计算方法如下:

式中:Un,eps为结构承受载荷时第n个焊点与相邻单元的应变能;an,eps为第n个焊点与相邻单元在承受载荷时的位移列阵;Kn为第n个焊点与相邻单元的结构刚度矩阵。其中焊点与相邻单元的位移列阵表达式为
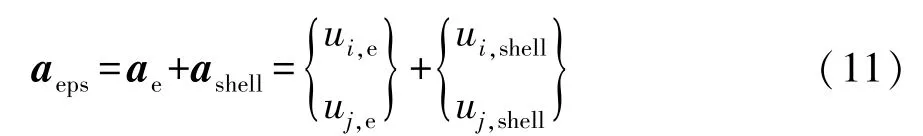
2.2 基于灵敏度排序的鲁棒性方法(RMC)建立
鲁棒性分析的最终目的是研究白车身性能对于焊点失效的敏感度。依照上述思路,建立如下离散焊点的不确定度(即焊点的失效概率)模型:
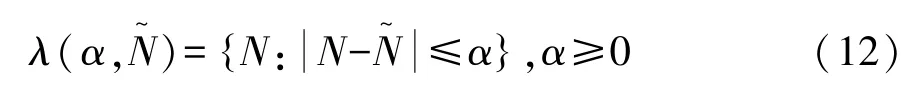
式中:N和分别为有效的焊点数量和总的焊点数量;α为失效焊点的不确定水平,这里可以简单地采用失效焊点的数量来代替。焊点主要影响的是白车身的动态刚度和静态刚度,本文中以1 阶模态和2阶模态表征白车身的动态刚度,以静态扭转刚度和静态弯曲刚度来表征白车身的静态刚度。则焊点的鲁棒性函数可以表示为
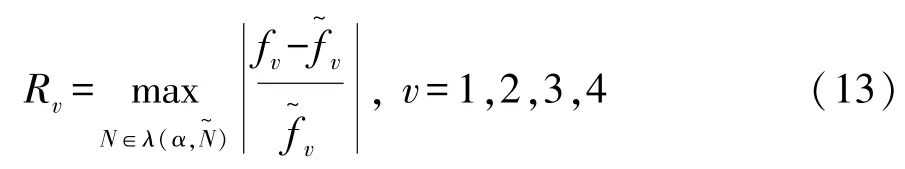
根据以上思路,可以得到本文建立的基于焊点灵敏度排序的鲁棒性分析方法(RMC)的基本计算流程,如图2 所示。

图2 RMC 方法计算流程
3 RMC 鲁棒性分析方法的验证
3.1 系统描述
本文中研究对象为某国产轻型客车的白车身,如图3 所示。该车型为非承载式车身,车架对于整车刚度的影响较大,为了更加明晰地研究焊点鲁棒性对于车身本体的刚度影响,故验证过程中未将车架考虑在内。该车身共包含9 462 个点焊单元,焊点的位置分布如图4 所示。

图3 某国产轻型客车白车身

图4 白车身焊点布置位置
3.2 有限元模型建立与试验验证
将三维实体模型以STP 格式导入到有限元前处理软件Hyper-mesh 中进行有限元网格的划分,网格全部采用SHELL 单元进行划分,建立的白车身有限元模型(不包括焊点)如图5 所示。

图5 白车身有限元模型(不包括焊点)
为了对焊点进行准确模拟,本文中采用被广泛验证的C-WELD 单元,并将焊点与相邻单元作为整体考虑的模型,详细对比研究可以参见相关文献[19-22],限于篇幅及本文研究重点,此处不对建模方法进行赘述。最终建立的白车身有限元模型(包含焊点)如图6 所示。

图6 白车身有限元模型(包含焊点)
为了验证本文所建立的有限元模型的正确性,本文中利用所建立的有限元模型进行仿真计算并进行相应的试验验证,主要包括白车身模态仿真试验、白车身静态扭转仿真试验和白车身弯曲仿真试验。仿真采用Hyper-Works 软件进行,部分试验过程设备如图7~图9 所示。仿真与试验结果对比如表1所示。

图7 白车身模态试验

图8 白车身静态扭转测试系统

图9 模态试验激振器(X 方向)
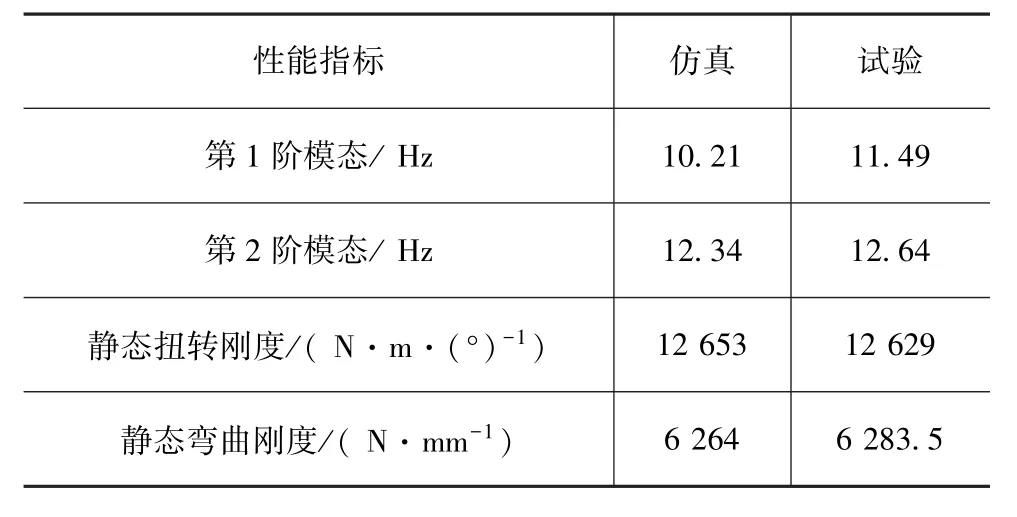
表1 白车身仿真与试验结果对比
以上结果说明,试验与仿真结果具有较好的一致性,说明本文建立的白车身有限元模型较为精确,并能获取较为准确的结果,可以应用于后续研究和分析。
3.3 焊点灵敏度排序结果的获得
通过上述有限元计算可得各个焊点对于不同性能指标的灵敏度分布,如图10~图13 所示。
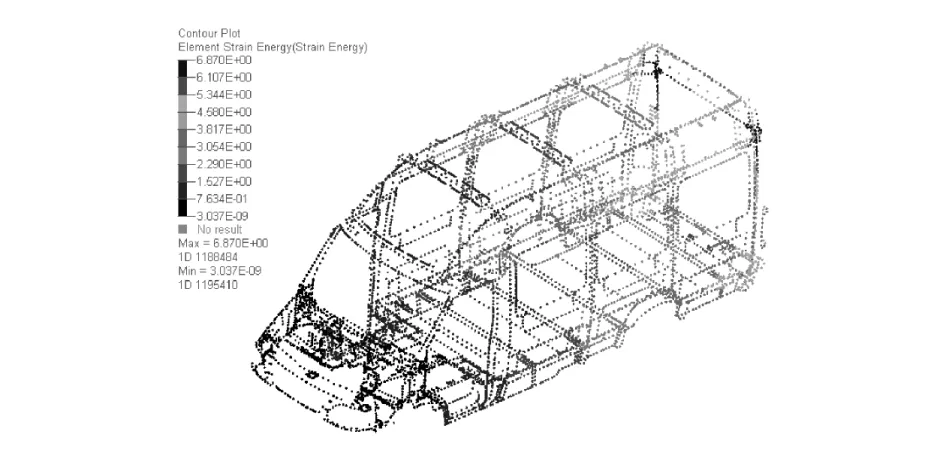
图10 焊点对1 阶模态的灵敏度结果

图11 焊点对2 阶模态的灵敏度结果
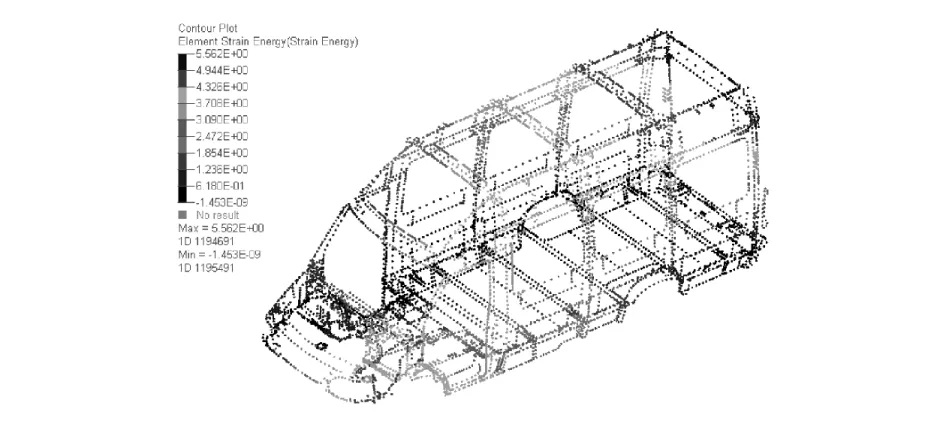
图12 焊点对静态扭转的灵敏度结果
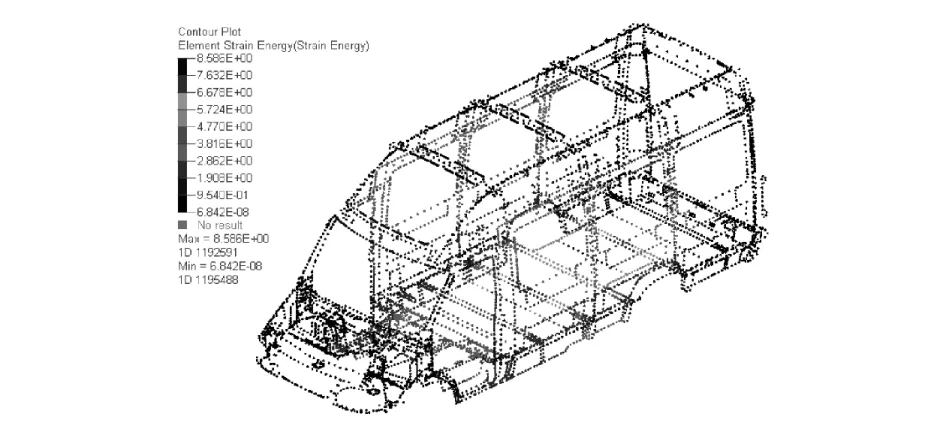
图13 焊点对静态弯曲的灵敏度结果
根据以上计算结果即可对白车身9 462 个焊点按照灵敏度的值进行降序排列,从而可以知道哪些焊点对白车身性能具有最高的灵敏度,该焊点即可确定为最大可能失效点。
3.4 RMC 方法与MC 方法的对比验证
为了验证本文提出的RMC 方法的效果和效率,本文中以某轻型客车白车身的焊点分布作为对象,分别采用传统MC 方法和本文提出的RMC 方法获取鲁棒性曲线并进行对比。
分别针对30 个焊点失效、60 个焊点失效和100个焊点失效这3 种工况的鲁棒性进行对比分析,参考相关研究成果[23-24],传统 MC 方法选取 75 个抽样进行计算,RMC 方法在每一次迭代中选取10 个失效焊点进行计算。两种方法获取的鲁棒性对比结果如图14~图17 所示。其中R1表示以白车身1 阶模态频率作为性能指标的鲁棒性,R2表示以白车身2阶模态频率作为性能指标的鲁棒性,R3表示以白车身静态扭转刚度作为性能指标的鲁棒性,R4表示以白车身静态弯曲刚度作为性能指标的鲁棒性。

图14 鲁棒性R1 对比结果
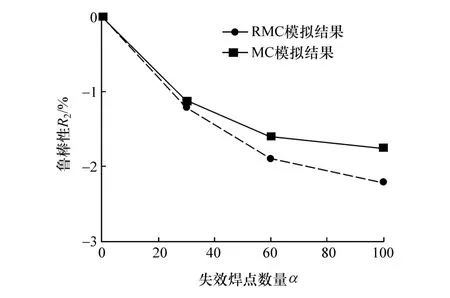
图15 鲁棒性R2 对比结果
由图可见:
(1)采用MC 方法和RMC 方法所获得的鲁棒性曲线趋势一致,但是MC 方法获取的鲁棒性结果偏小,由于鲁棒性函数Rv(v= 1,2,3,4)表征的是在所有可能性中焊点失效导致的相应性能的最大偏移率,这就意味着本文提出的RMC 方法的精度要高于采用75 个样本点的MC 方法;

图16 鲁棒性R3 对比结果

图17 鲁棒性R4 对比结果
(2)在获取以上鲁棒性曲线的过程中,RMC 方法共须进行10 次白车身性能分析,而MC 方法则须进行75×3 =225 次白车身性能分析,所以采用RMC不仅能获得具有较高精度的鲁棒性结果,而且还大大提高了鲁棒性计算的效率;
(3)随着失效焊点数量的增多,两种方法获得的结果差异逐渐增大,这主要是因为随着样本数量的增加,MC 方法需要更多的抽样才能获取较高精度的结果,而RMC 方法则没有这样的约束条件。
4 结论
传统的蒙特卡洛鲁棒性分析方法存在着成本高、效率低、精度严重依赖抽样数量的缺点。为了克服上述缺点,本文中在蒙特卡洛重要抽样理论的基础上,结合焊点灵敏度排序提出了一种新的鲁棒性分析方法(RMC),并以某国产轻型客车白车身为例进行了对比验证,得出如下结论:
(1)本文提出的基于焊点灵敏度排序的鲁棒性分析方法是一种高效、低成本的鲁棒性分析方法,该方法采用较少的成本即可获得较高的精度;
(2)本文提出的鲁棒性分析方法对于大样本容量的案例具有更强的适用性,可以广泛应用于白车身焊点的优化问题,同时对于类似的工程问题也具有较强的实用价值和借鉴意义。
