电动车用轮毂电机的负载磁场解析计算*

张河山，邓兆祥，杨明磊，罗 杰，徐 进

(1. 重庆交通大学交通运输学院，重庆 400074；2. 重庆大学汽车工程学院，重庆 400044；3. 同济大学汽车学院，上海 200092)

前言

应对全球能源危机和环境恶化的严峻挑战，近年来各种形式的电动汽车成为世界各国汽车工业发展的热点。其中，轮毂电机驱动的电动汽车成为一个新的研究方向[1－2]。在这种驱动方式下，驱动电机、传动机构以及制动系统最大化地集成在车轮轮毂内，实现了四轮的独立控制，取消了传统燃油车的变速器和离合器等传动部件，极大简化了整车布置，提升了控制效率，有利于实现机电一体化[3－4]。

永磁电机具有效率高、功率密度高和寿命长等特点，广泛应用于电动汽车的驱动电机。直驱式轮毂电机通常采用外转子永磁电机，为降低转子质量和体积，永磁体通常采用表贴式和表面嵌入式两种安装方式，后者相比于前者具有较多优势，例如表面嵌入式磁体结构能够提供磁阻转矩，减小涡流损耗，拥有较好的弱磁能力以及较高的机械强度[5－6]。因此本文中的轮毂电机也采用外转子表面嵌入式磁体结构。由于轮毂电机定转子铁芯都为开槽结构，且定子槽为半开口结构，绕组为分数槽集中式布线。建立准确刻画定转子开槽效应的磁场解析模型难度较大，特别是气隙磁场的准确性难以保证。

常用的分析方法有有限元法和解析法。有限元法作为一种常用的分析方法具有很多优势，例如可以构建较复杂的几何结构，考虑铁磁材料的非线性特性以及磁饱和效应。但是在电机设计初期和性能优化阶段，电机的结构和尺寸变化时须反复建模、设定边界条件、划分网格，建模过程复杂，计算耗时、耗资源。而解析法具有较高的灵活性，在改变设计参数时，无须反复建模，具有较高的效率，方便探讨设计变量与性能参数的映射关系。常用的解析法有等效磁路/网络、保角变换、子域分析技术。等效磁路/网络法可以考虑铁磁材料非线性特性以及磁饱和效应，但只能粗略计算电机性能，不能处理复杂磁场问题，不能考虑齿槽效应，计算误差较大，通常用于初始设计阶段[7]。将永磁体等效为面电流，通过保角变换将有槽的求解域转化为无槽域，通过坐标变换来考虑齿槽效应[8]。但忽略了由于共形映射引起的磁体形状和气隙磁密积分路径的变形，导致齿槽转矩的计算误差[9]。基于泊松和拉普拉斯方程的子域分析技术具有很高的精度，因为它可以准确刻画复杂的几何结构，准确计算定转子开槽对气隙磁场的影响[10－11]。因此，子域分析技术被广泛应用于各种类型的电机磁场分析。文献[12]～文献[15]中利用子域分析技术集中研究了定子无槽的表面嵌入式永磁电机，将电枢绕组假设为面电流，可以预测空载气隙磁密、电枢反应磁场、电磁转矩和永磁体损耗等性能。文献[16]中结合子域分析技术和保角变换，考虑了表面嵌入式永磁电机的转子偏心和磁饱和效应，但是定子铁芯被假设为无槽结构，导致不能精确计算齿槽转矩和电磁转矩。在此基础上，文献[17]～文献[20]中又研究了表面嵌入式永磁电机定子开槽效应，可以研究定子开槽对气隙磁场的影响。其中，文献[17]中利用矢量磁位和子域分析技术建立了内转子永磁电机的解析模型，预测了空载、电枢反应和负载工况下的气隙磁场分布，其缺点是将定子槽假设为开口槽(即槽开口宽度角与定子槽宽度角相等)，未考虑定子槽开口求解域，不能准确计算齿槽转矩。文献[18]中利用子域分析技术研究了永磁无刷电机的定子开槽效应，并增加了槽开口子域，解析模型更完善，可以预测空载和电枢反应下的气隙磁场分布。文献[19]中又推导了转矩的表达式，并计算了负载气隙磁密、齿槽转矩和电磁转矩。文献[20]中考虑了轴向磁通电机的定子开槽效应，在直角坐标系中计算了负载气隙磁场分布。文献[5]中增加了“转子空气槽”，将其应用到高凸极率的内转子永磁电机的解析建模中，这种转子结构可以提高电感凸极率，从而增大磁阻转矩，同时获得较宽的调速范围。

上述解析计算模型有助于表面嵌入式永磁电机的性能分析和优化设计，但不适用于本文中研究的车用轮毂电机，因其具有外转子嵌入式永磁体、分数槽集中式绕组、定子槽为半开口槽等复杂的拓扑结构。因此本文中利用麦克斯韦方程和子域分析技术建立了车用轮毂电机的负载磁场解析模型，考虑了定子开槽效应，特别是定子槽开口子域。为建立快速且精确的磁场计算模型，将整个磁场求解域划分为4 类子域，即电枢定子槽、槽开口、气隙和永磁体转子槽。首先，根据激励源的不同，在各子域建立矢量磁位的麦克斯韦方程，并利用分离变量法求解各子域的矢量磁位的通解。然后，利用相邻子域间的边界条件得到矢量磁位的谐波系数。最后，解析预测了轮毂电机的磁场分布、反电动势、电感、齿槽转矩以及输出转矩等性能，并对比了开口槽结构的解析计算结果。利用有限元法和样机试验验证了解析法的正确性。进一步研究了永磁体极弧系数和槽开口宽度对齿槽转矩和输出转矩的影响规律。

1 磁场解析模型

1.1 电机几何结构与基本假设

图1 为课题组自主研发的分布式驱动电动汽车驱动轮总成，轮内集成了驱动电机、挠性传动机构、电机悬架以及电子机械制动等，驱动力直接由电机经过挠性传动机构传递至车轮，整车布置更加灵活。本文中的研究重点是利用子域分析技术对轮毂电机进行解析建模与性能研究。为简化解析建模，作如下假设:

(1)忽略涡流效应和端部效应；

(2)定转子铁芯的磁导率为无穷大；

(3)矢量磁位和电流密度只有z轴方向的分量；

(4)永磁体材料为线性退磁特性；

(5)定转子铁芯和永磁体的电导率为零。

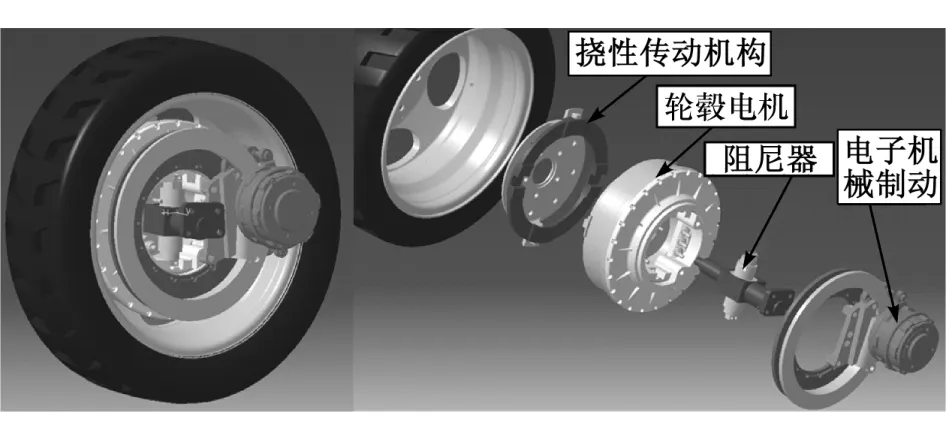
图1 轮毂电机驱动的电动车轮总成

所研究的轮毂电机为48 槽16 对极，外转子表面嵌入式磁体结构。图2 给出开口槽和半开口槽两种结构作对比分析。其中图2(a)中没有单独划分槽开口子域，即定子槽和槽开口宽度角相等，可参考文献[21]中的定子槽形状。将图2(b)中的轮毂电机整个求解域划分为4 类子域，分别为:定子绕组槽(子域Ⅰ)、槽开口(子域Ⅱ)、气隙(子域Ⅲ)和永磁体转子槽(子域Ⅳ)。定子槽和转子槽的中心位置分别定义为

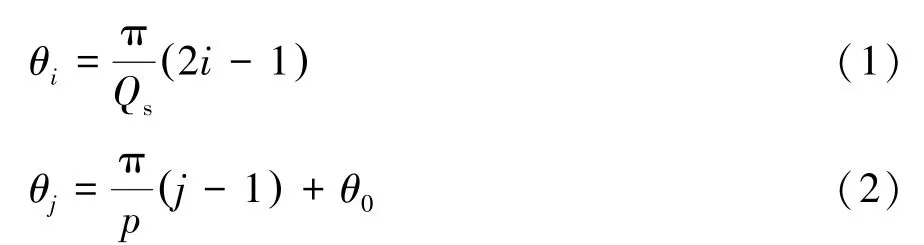
式中:Qs为定子槽数；p为转子极对数；θ0为转子初始位置。

1.2 激励源

对于表面嵌入式磁体结构，磁化强度呈非周期性分布。因此利用奇延拓将磁化强度补充为周期信号，如图 3 所示。

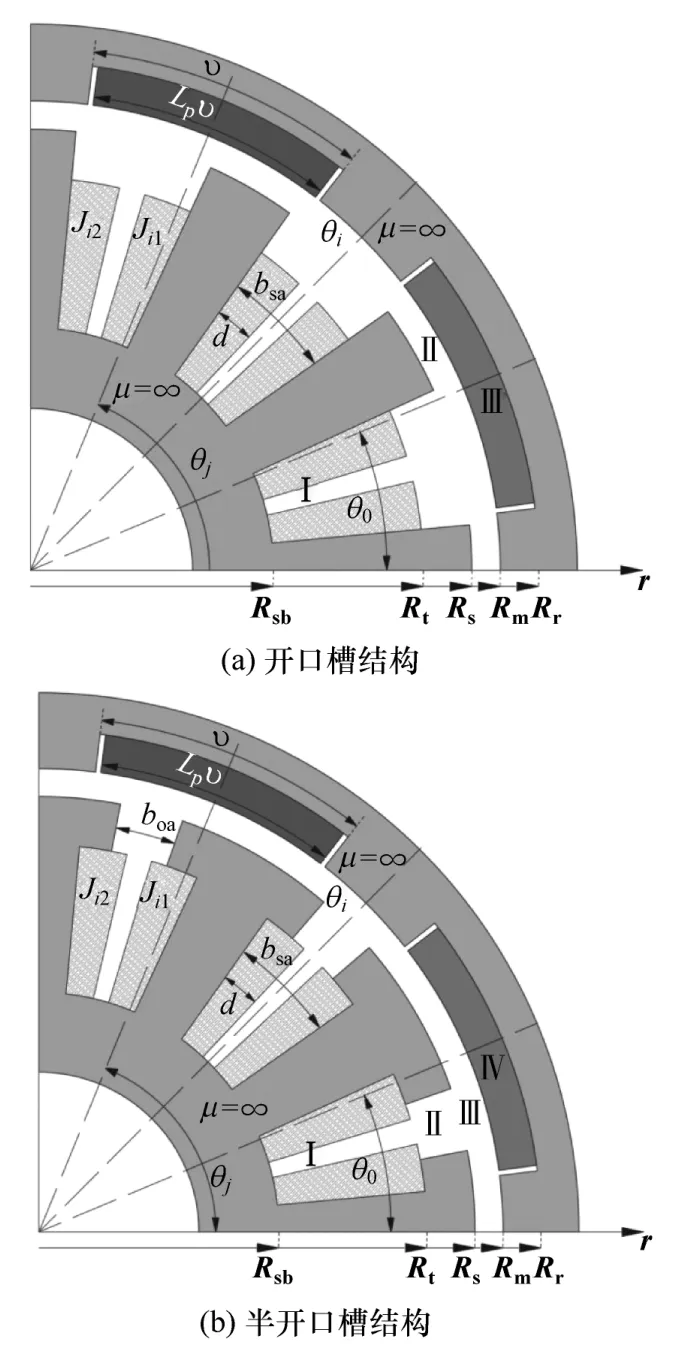
图2 轮毂电机子域模型

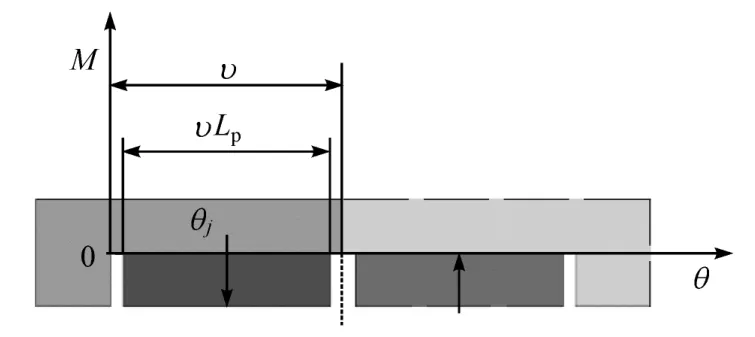
图3 奇延拓后的磁化强度分布

根据式(3)，第j个转子槽内的永磁体磁化强度Mj可以表示为径向和切向分量的矢量和。当永磁体径向充磁时，磁化强度的径向和切向分量如式(4)和式(5)所示。当然，也可以处理平行充磁和Halbach 充磁方式。

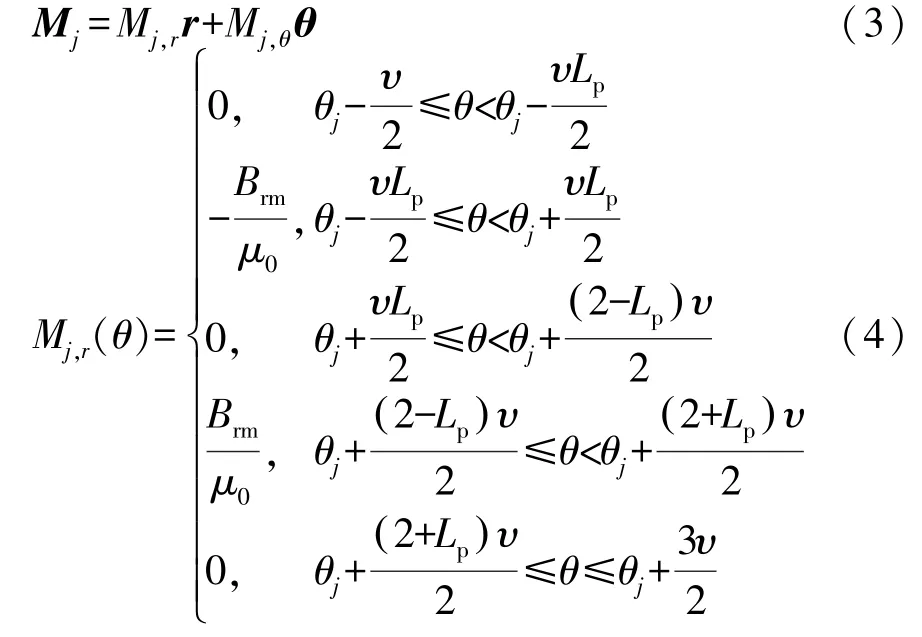
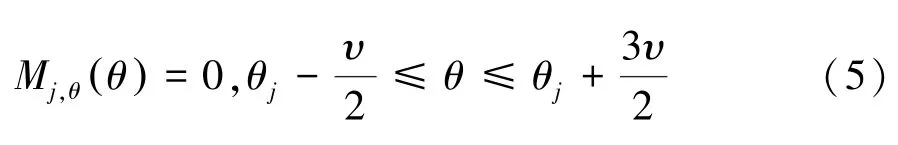
式中:υ为转子槽宽度；υLp为永磁体极弧系数；Brm为永磁体剩磁；μ0为真空磁导率。

根据周期性，可以将其转换为傅里叶级数形式:

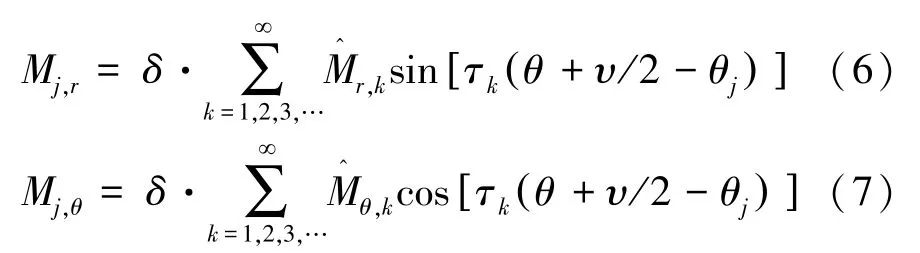
其中:δ＝ (－1)j－1；τk＝kπ/υ

式(6)和式(7)的傅里叶系数分别为

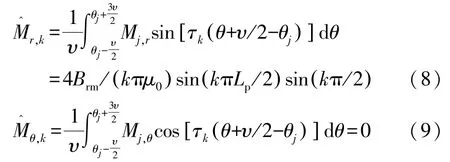
轮毂电机为双层绕组，根据周期性，第i个定子槽的电流密度可以表示为傅里叶级数形式:

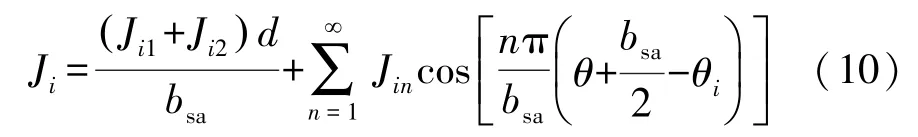
式中:Ji1和Ji2为定子槽内左右两侧绕组的电流密度；bsa为定子槽的宽度；d为单侧绕组的宽度。谐波系数Jin可以由下式计算:

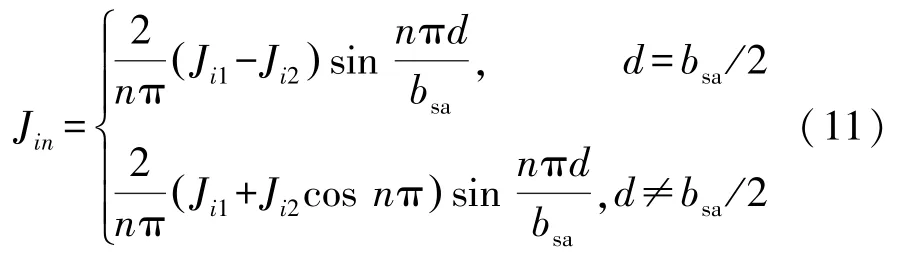
轮毂电机采用分数槽集中式绕组，图4 示出定子绕组的连接图，对应的绕组排列矩阵为

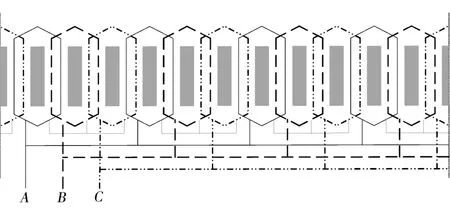
图4 定子绕组连接图

1.3 各子域的矢量磁位通解

根据激励源的不同，各子域的磁场控制方程不一样。子域Ⅰ(定子绕组槽)和子域Ⅳ(永磁体转子槽)的矢量磁位满足Poisson 方程，子域Ⅱ(槽开口)和子域Ⅲ(气隙)的矢量磁位满足Laplace 方程，如式(14)所示。

利用分离变量法，可以得到各子域的矢量磁位通解，其表达式具体如下。

(1)定子绕组槽(子域Ⅰ)

其中

式中Rt和Rsb分别为定子槽顶部和底部的半径。

(2)槽开口(子域Ⅱ)

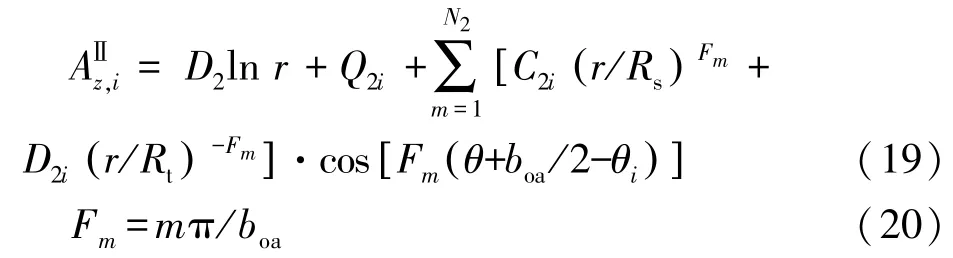
式中:Rs为定子铁芯的外径；boa为槽开口宽度。

(3)气隙(子域Ⅲ)

式中Rm为永磁体的内径。

(4)永磁体转子槽(子域Ⅳ)

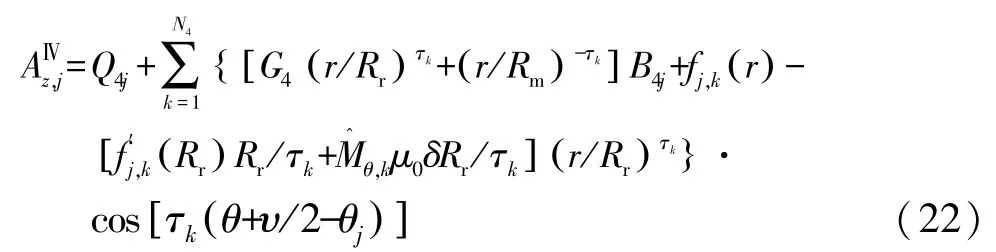
其中

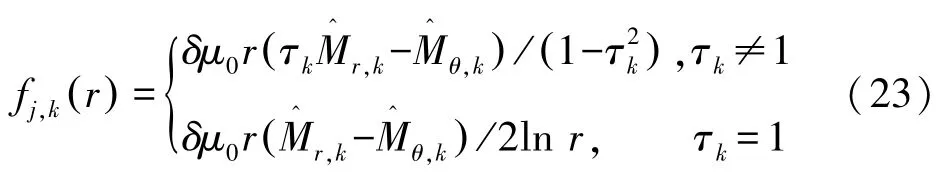
式中Rr为永磁体的外径。

1.4 各子域的磁通密度

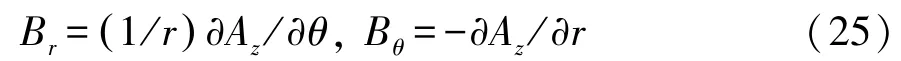
(1)定子绕组槽(子域Ⅰ)

(2)槽开口(子域Ⅱ)

(3)气隙(子域Ⅲ)

其中:

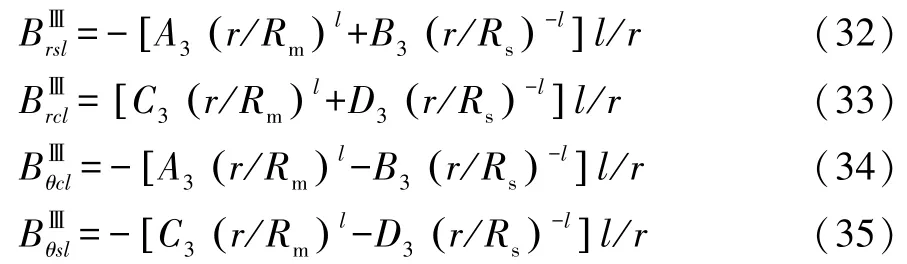
(4)永磁体转子槽(子域Ⅳ)

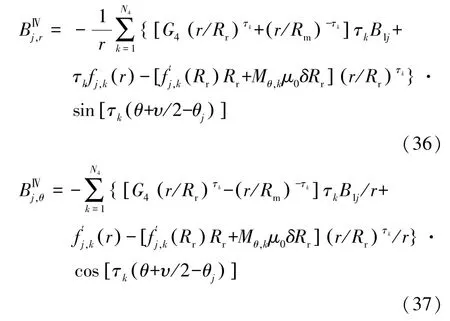
1.5 边界条件

前文矢量磁位中的待求解系数可以通过相邻子域间的边界条件确定，其基本原理是根据磁场的连续性，即相邻子域交界面的法向磁密和切向磁场强度相等，具体表达式如下。

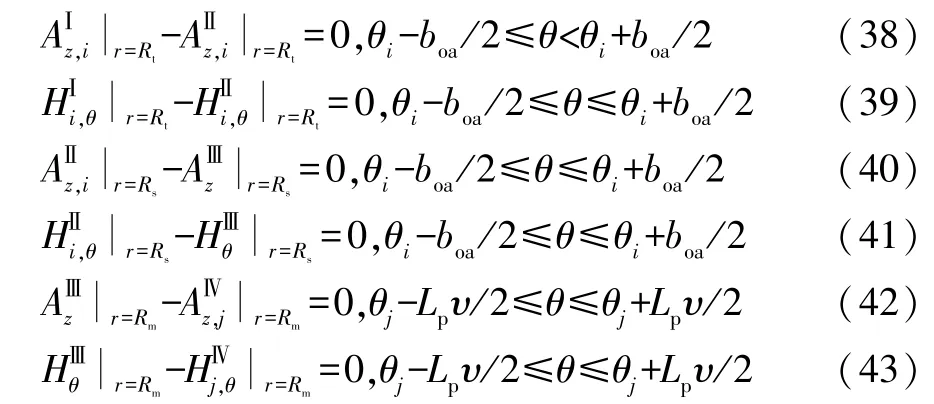
联合式(38)～式(43)可以组成多元矩阵方程，通过求解矩阵方程得到矢量磁位中的直流项系数(Q1i，D2，Q2i，Q4j) 和谐波系数(D1i，C2i，D2i，A3，B3，C3，D3，B4j)，进而得到各子域的矢量磁位通解。

2 解析计算与验证

为验证本文所提解析法的正确性，在MATLAB 软件中建立轮毂电机的解析模型，利用ANSYS/Maxwell软件建立轮毂电机二维有限元模型。表1 给出轮毂电机的主要设计参数。电机转速为600 r/min，峰值相电流为45 A。为保证计算精度，有限元模型中的电枢绕组、永磁体、定转子铁芯等各部件网格剖分单元最大尺寸为1 mm，仿真步长为 6×10－5s。由于轮毂电机的齿槽转矩和输出转矩均是通过气隙磁场得到的，设置较大的气隙子域谐波次数，获得精确的气隙磁场分布。为兼顾计算精度和效率，解析模型中各子域的最高谐波次数分别设置为:N1＝30，N2＝30，N3＝500，N4＝30。

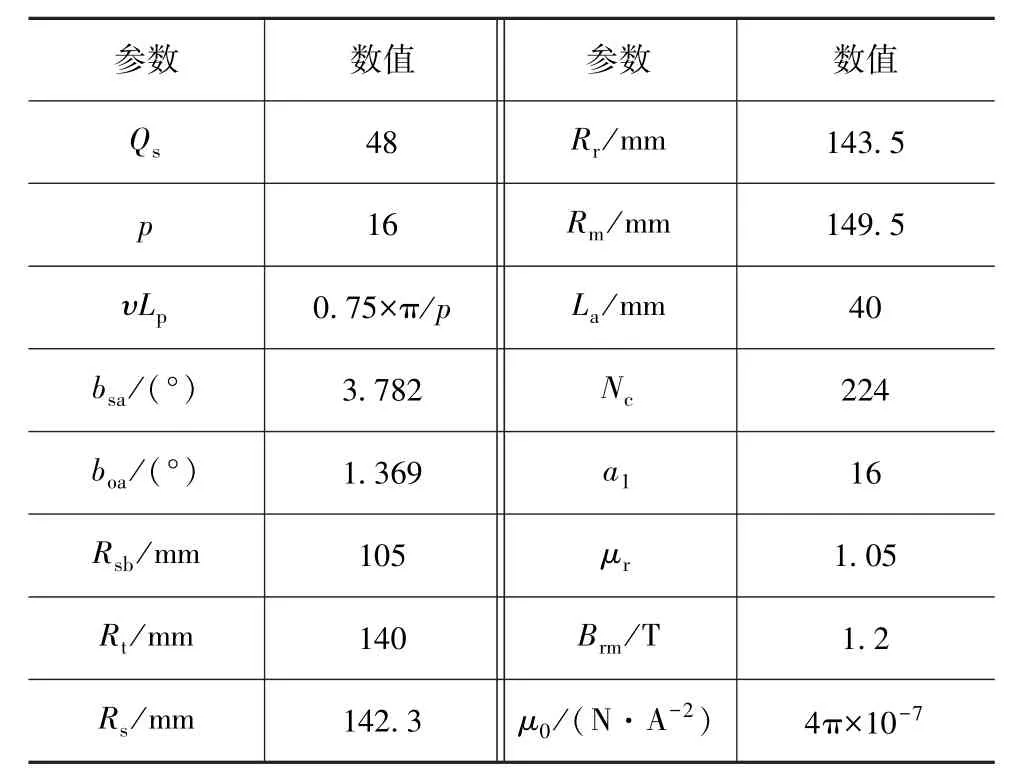
表1 轮毂电机的主要参数

2.1 磁密分布

准确计算气隙磁场分布对预测轮毂电机齿槽转矩、输出转矩等电磁性能至关重要。图5 给出有限元法计算的负载工况下磁密云图和磁力线分布情况。图6～图8 分别为空载、电枢反应和负载工况下气隙中间位置(r＝(Rs＋Rm)/2)的磁密分布。可以看出，解析计算结果与有限元结果吻合较好，证明本文所提解析模型具有较高精度。同时对比了开口槽结构的计算结果，当不考虑齿尖时，气隙磁密曲线产生了较大的畸变。

图5 负载工况的磁密云图和磁力线图

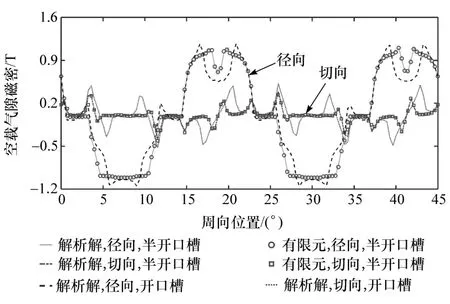
图6 空载气隙磁密

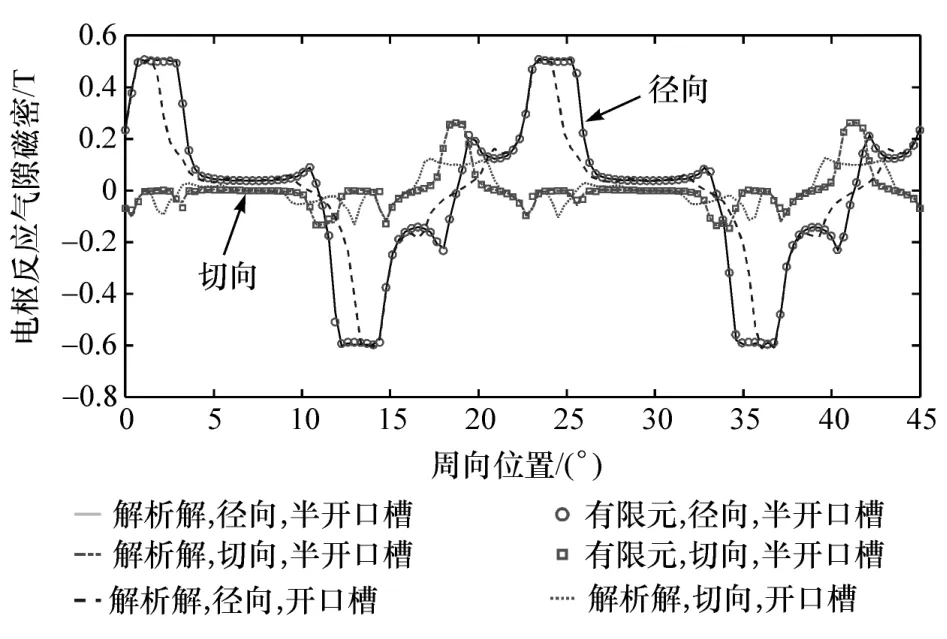
图7 电枢反应气隙磁密

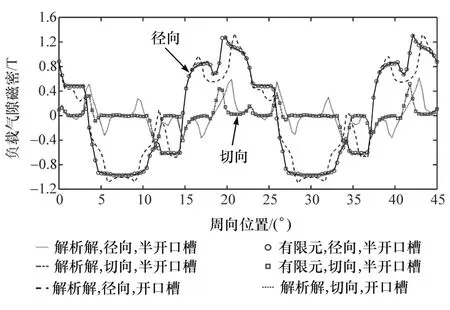
图8 负载气隙磁密

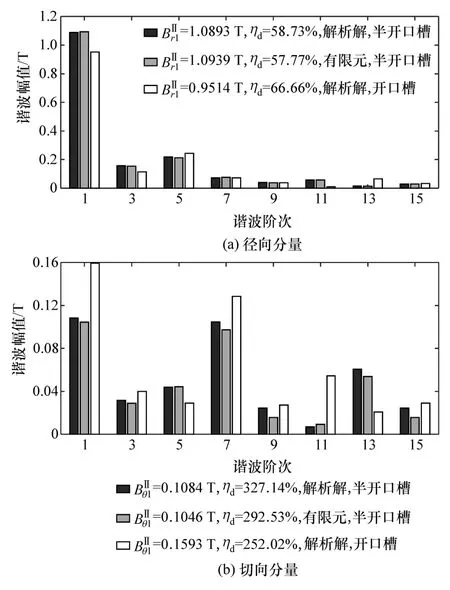
图9 负载气隙磁密谐波谱

为评估气隙磁密曲线的正弦特性，定义谐波畸变率见式(44)。图9 为负载气隙磁密的谐波谱。可以看出解析模型计算的各阶次幅值以及谐波畸变率均与有限元分析结果高度一致，进一步证明了解析模型的准确性。开口槽结构的气隙磁密谐波畸变率较大。

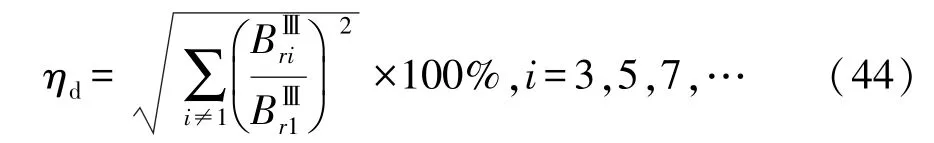
图10～图12 分别为负载工况下，定子槽、槽开口和转子槽内的磁场分布情况。可以看出解析解与有限元结果吻合较好。而开口槽结构忽略了齿尖的影响，其磁路将会发生变化，导致各子域中磁场分布也发生了改变，尤其从图11 可以看出，忽略齿尖后的磁密曲线发生了巨大的变化。

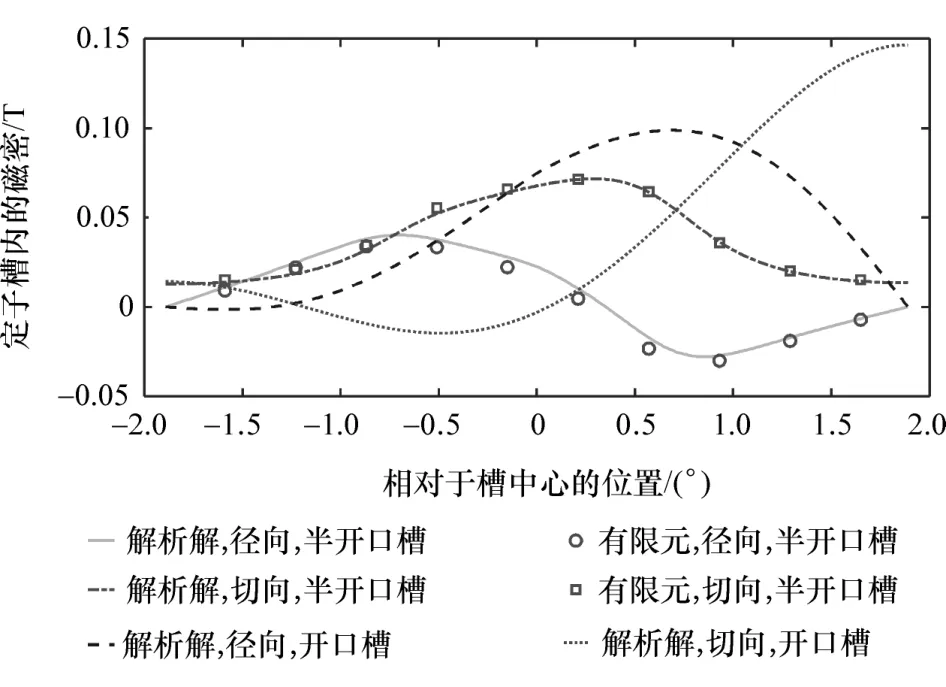
图10 定子槽内的磁密分布(r ＝Rt－1 mm)

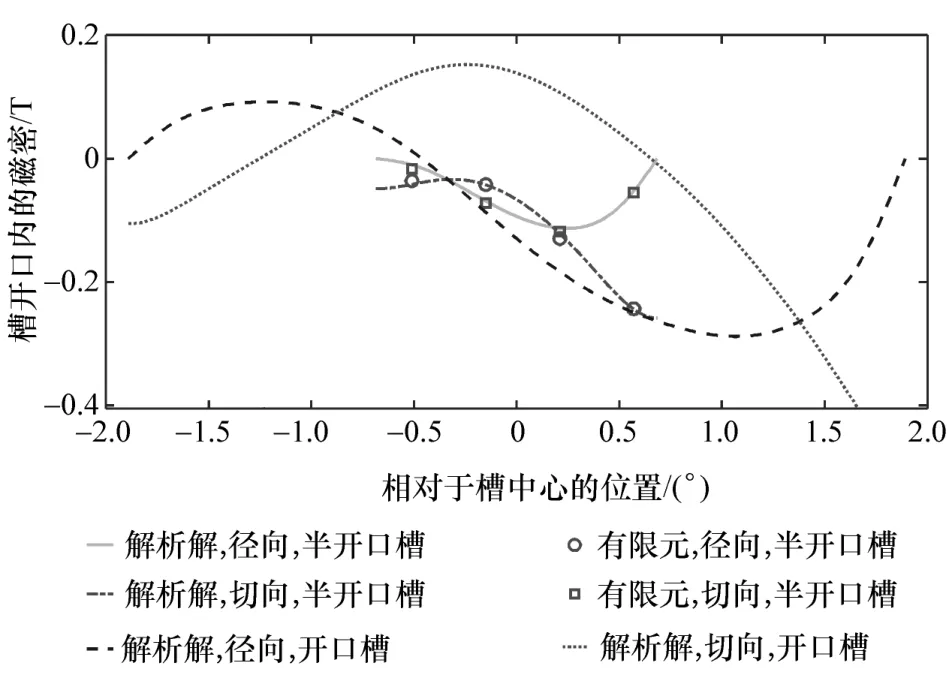
图11 槽开口内的磁密分布(r ＝Rs－1 mm)

图12 转子槽内的磁密分布(r ＝Rm＋1 mm)

2.2 磁链、反电势和电感

对于双层绕组，左、右侧线圈边的磁链可以从定子槽(子域Ⅰ)的矢量磁位得到。

三相磁链可以按下式计算:

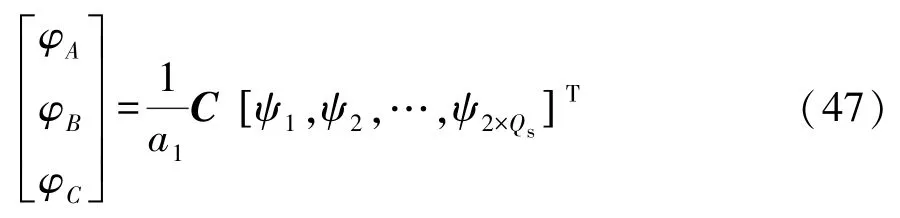
式中:La为铁芯轴向长度；a1为并联支路数。

图13 示出两种结构的A相磁链对比。与半开口槽结构相比，开口槽结构的磁链幅值较低。

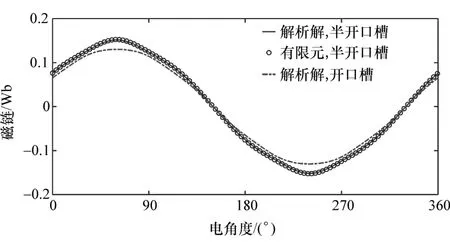
图13 A 相磁链

三相反电动势可以通过磁链对时间求导计算得到

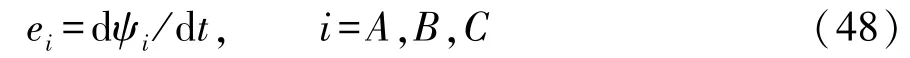
由于轮毂电机为凸极转子，因此电感随转子位置的变化而变化。令iA＝ 45 A，iB＝iC＝ 0，Brm＝ 0，A相自感和互感可通过式(49)计算。图14 为随转子位置变化的三相绕组的电感，可见解析解与有限元结果相当吻合，开口槽结构的A相自感降低，A相与B相和C相的互感增大。

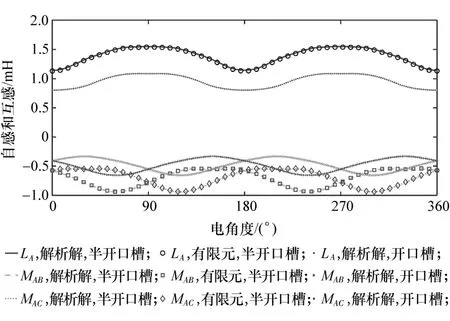
图14 随转子位置变化的绕组电感

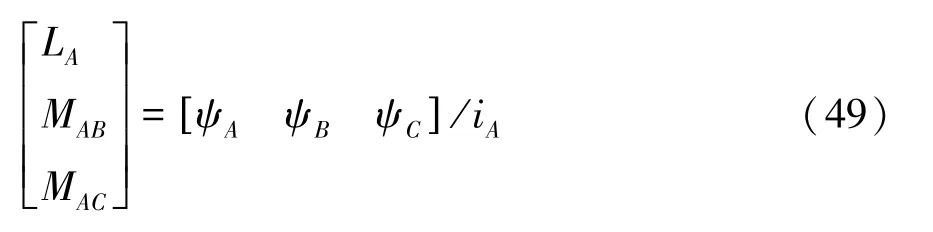
2.3 齿槽转矩和输出转矩

利用气隙磁密，根据Maxwell 张量法计算轮毂电机的转矩，包括空载工况下的齿槽转矩和负载工况的输出转矩，计算公式为

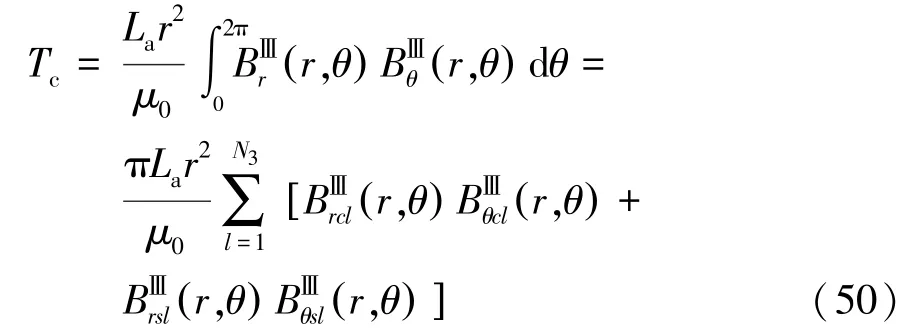
其中r＝ (Rm＋Rs)/2

图15 和图16 为齿槽转矩和输出转矩对比图。解析模型预测波形的幅值和相位与有限元结果一致，进一步证明了解析模型的正确性。同时对比开口槽结构的计算结果可知，其较大的槽口宽度导致气隙磁密产生严重的畸变，使齿槽转矩和输出转矩脉动变大。气隙面积增大，气隙内磁感应强度降低，导致输出转矩平均值变小。

图15 齿槽转矩

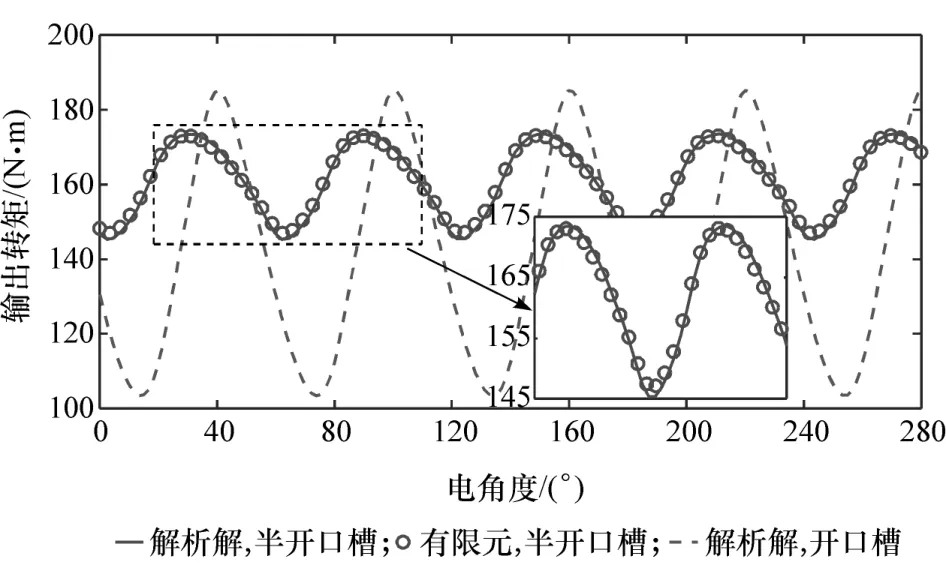
图16 输出转矩

为进一步验证本文所提解析算法的正确性，对轮毂电机样机进行加工制造，如图17(a)所示，并搭建试验台架，如图17(b)所示，图17(c)为轮毂电机驱动的电动车轮总成。首先，对样机进行开路试验，利用测功机拖动样机的方式，进行空载反电动势的测量，将轮毂电机转速拖动至600 r/min，测量相反电动势。如图 18 所示，解析计算结果、有限元结果和样机实测结果的趋势与峰值较吻合，但也存在一定误差，其原因是解析法和有限元法对电机模型进行了一定的简化处理；另外，试验台架的机械损耗、摩擦以及测量仪器的精度会产生误差。

图17 轮毂电机样机与试验台架

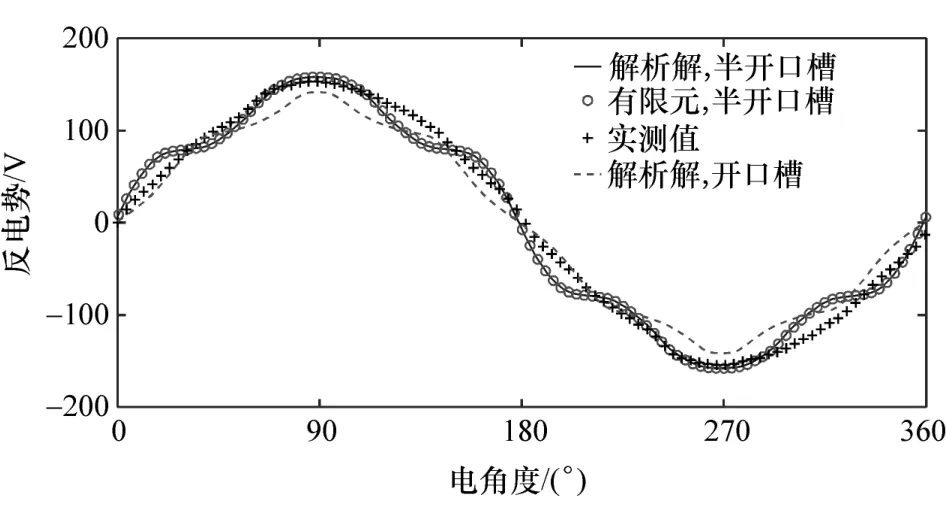
图18 空载反电动势

此外，利用轮毂电机综合性能试验台对样机进行动态性能测试。图19 为额定工况下轮毂电机输出转矩/功率与转速的特性曲线。当电机转速小于等于600 r/min 时，在恒转矩区输出转矩近似等于158 N·m，加速到基速后通过弱磁技术可获得更高的转速，让电机工作于恒功率区。可以看出解析结果与实测值较吻合，证明本文所提出的解析算法具有较高的精度。

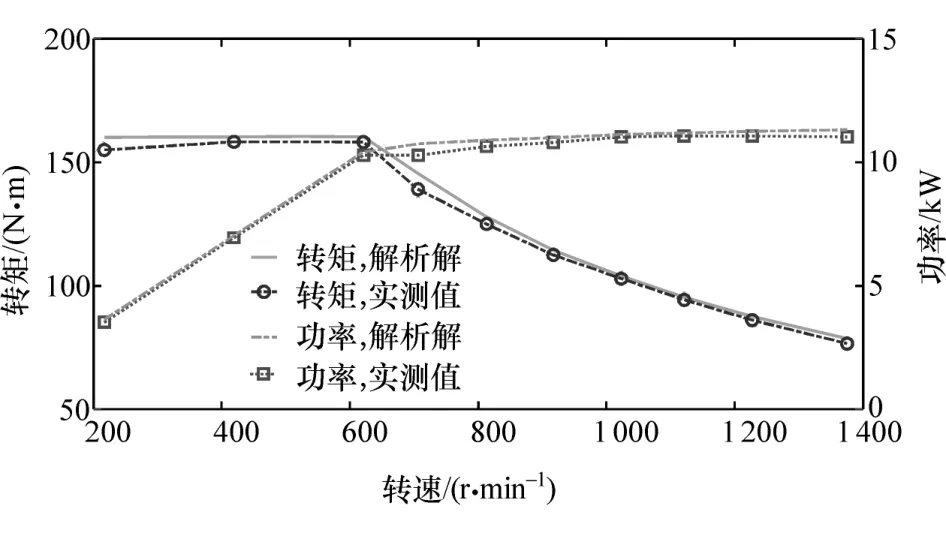
图19 转矩/功率与转速的特性曲线

3 影响因素分析

解析法的优点是在改变设计参数时，无须重复建模，便可对不同结构尺寸的电机进行性能优化，计算效率高。因此，利用解析模型进一步研究极弧系数和槽开口宽度对齿槽转矩峰值、输出转矩平均值和输出转矩脉动的影响规律。其中，转矩脉动Tvib可由输出转矩Tc计算:

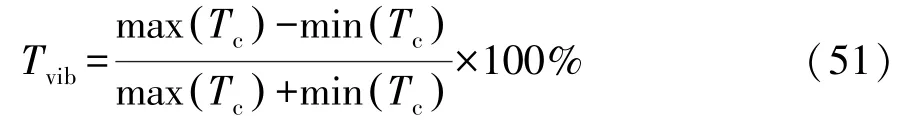
图20 为极弧系数υLp和槽开口宽度boa对齿槽转矩的影响。从图可以看出，极弧系数从0.6 增大至0.9，齿槽转矩先减小后增大。齿槽转矩随槽开口宽度的增大，先增大后略微减小，总体呈增大的趋势。另外，当极弧系数确定时，齿槽转矩基本上都是随槽开口宽度的增大而增大。当极弧系数为0.775，槽开口宽度为0.969°时，齿槽转矩最小为1.912 N·m。

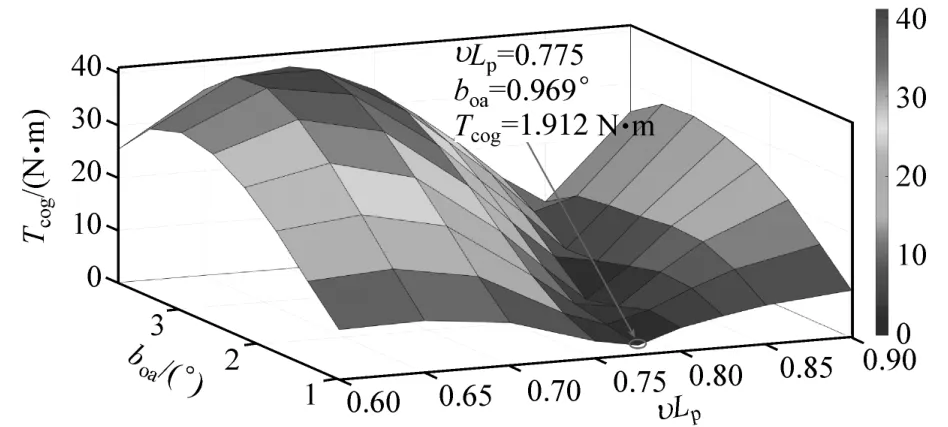
图20 极弧系数和槽开口宽度对齿槽转矩峰值的影响

图21 为极弧系数和槽开口宽度对输出转矩平均值的影响。从图可知，极弧系数越大、槽开口宽度越小时，输出转矩平均值越大。当极弧系数为0.9，槽开口宽度为0.969°时，输出转矩平均值最大为177.65 N·m。

图21 极弧系数和槽开口宽度对输出转矩平均值的影响

图22 为极弧系数和槽开口宽度对输出转矩脉动的影响。从图中可以看出，极弧系数和槽开口宽度对转矩脉动和齿槽转矩的影响趋势较接近，当极弧系数为0.825，槽开口宽度为2.169°时，输出转矩脉动最小为3.025%。

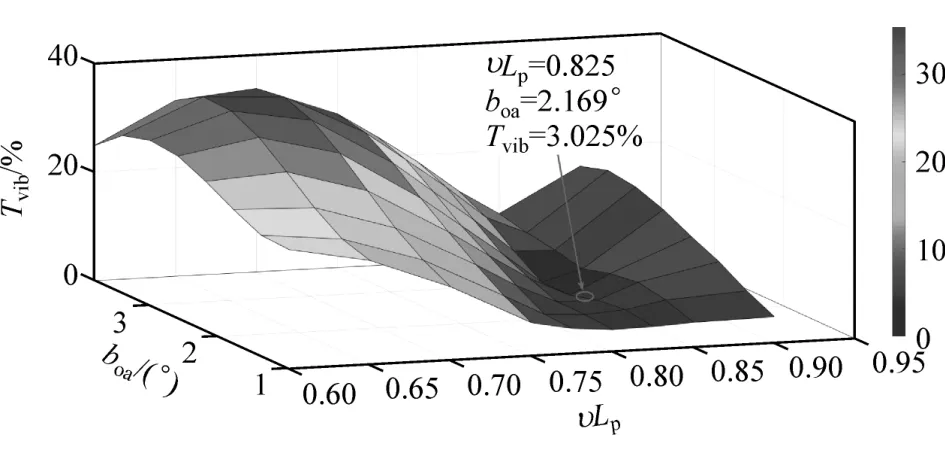
图22 极弧系数和槽开口宽度对输出转矩脉动的影响

综上，以较大的输出转矩平均值和较小的转矩脉动为优化目标，当该电机的极弧系数为0.825，槽开口宽度为2.169°时，输出转矩平均值从原样机的160.75 提高到165.08 N·m，转矩脉动从原样机的8.8%降至3.025%。另外，这也解释了前文开口槽结构的齿槽转矩和转矩脉动较大、转矩平均值较小的原因。

4 结论

利用子域分析技术建立了一台48 槽16 对极的轮毂电机解析模型。在二维极坐标系下，将电机求解域划分为4 类子域，通过在各子域求解拉普拉斯方程或泊松方程，并利用边界条件得到各子域的矢量磁位通解的解析表达式。计算了轮毂电机的气隙、定子槽、槽开口以及转子槽子域的磁场分布、电感、齿槽转矩以及输出转矩。利用有限元分析和样机试验验证了解析模型的准确性，并对比分析了开口槽结构的计算结果，发现齿尖结构对电机的影响十分显著，因此在构建电机的解析模型时，考虑齿尖结构是十分必要的。

进一步研究了极弧系数和槽开口宽度对齿槽转矩、输出转矩平均值和转矩脉动的影响，结果表明:当该电机的极弧系数为0.825，槽开口宽度为2.169°时，输出转矩平均值从原样机的160.75 提高到165.08 N·m，转矩脉动从8.8%降至3.025%，在削弱转矩脉动的同时获得了较大的输出转矩平均值。

所提出的解析建模方法是根据激励源和媒介的不同来划分子求解域，同样适用于直线电机、轮辐式电机和开关磁阻电机的解析建模，对于各类电机的性能分析具有较大的通用性。