“一题一课”，促进高阶思维发展

李国良

【摘 要】数学是研究数量关系与空间形式的科学。在《倍的认识》单元复习中，以“倍”的本质属性——关系为主线，采用“一题一课”的形式，梳理出单元的知识结构，在“一题”的变化中促进知识的生长，在多重表征、多维观察、多型练习的复习路径中，立体化呈现量与量之间的不同关系，从而促进学生思维的提升、能力的发展。

【关键词】关系 一题一课 高阶思维

一、课前慎思

所谓“一题一课”，一般是指一节课中对一道题或一个材料的深入研究，挖掘其内在的学习素材，科学有序地组织学生进行数学探究活动，以此达到多维的目标过程。教师在研究此题的过程中使学生在较高认知水平层次上进行心智活动，促进其高阶思维的发展。数学复习课借助一课一题来展开教学，不仅能巩固知识、强化技能，还能帮助学生对已学的知识进行有效的梳理，形成结构化的知识体系，从而促进学生进行大概念的学习。

《倍的认识》单元是人教版数学三年级上册的内容，它涉及3个例题，分别是：例1——倍的含义，例2——求一个数是另一个数的几倍，例3——求一个数的几倍是多少。应该说，例1是本单元知识的“种子课”，通过建立和理解倍的概念来解决与倍有关的实际问题。笔者在翻阅人教版数学教材时发现，与倍相关的知识教材仅安排了求倍数、几倍数和一倍数等比较简单的、一步解决问题的题目，而到了五年级上册《简易方程》单元中出现了如：“地球的表面积为5.1亿平方千米，其中，海洋面积约为陆地面积的2.4倍，地球上的海洋面积和陆地面积分别是多少亿平方千米？”“果园里种着桃树和杏树，杏树的棵数是桃树的3倍，杏树比桃树多90棵，桃树和杏树各有多少棵？”等等这样用“和倍或差倍”来解决的实际问题。我们认为，这与三、四年级的学习存在着一定的脱节现象，从大概念的视角来看，需要建构起从算术思维到代数思维的过渡，让其能在原有认知基础上得到发展。

二、巧设一题

采用“一题一课”形式来促进学生思维的发展，关键是对这“一题”的设计，它所呈现的是对知识“来龙去脉”的梳理，还有对知识“瞻前顾后”的把握。根据对教学内容的分析与教材的梳理，笔者以为，教师复习时可以进一步借助圈一圈、画一画等方法多维度巩固倍的概念，在表征中发展学生的幾何直观能力，帮助其理解从不同角度观察来建构倍的意义，发展数学模型。一题设计如下：

学生在表征的过程中，不仅可以从部分与部分的角度分析，也可以从部分与整体的角度分析。部分与部分之间的倍数关系是教材研究倍的知识起点，部分与整体之间的倍数关系是和倍关系的知识起点，这样，学生能从不同的角度立体化呈现倍的意义，为后续的用方程解决问题做准备，逐步建立起方程思想，最终形成一个立体网状、动态关联的系统。

三、实践探索

数学复习课应具有面向全体学生又兼顾两头的差异教学理念，需建立起低起点进入、高思维出来的学习路径。众所周知，数学是研究数量关系与空间形式的科学，而倍是两个量比较后产生的新的量，是学生学习相差关系后的一种新的关系，我们以“关系”为教学主题，针对“一题一课”的教学思路开展了实践探索。

（一）多重表征，深刻理解倍的意义

课始，教师出示核心题目，组织学生涂一涂、圈一圈，再填一填，然后列出算式，要求学生能用两种关系和两种不同的方法来完成。学生根据自己的认知水平很快表征出不一样的结果。

生1：涂色有2个，空白个数是涂色的3倍，6÷2=3;也可以说，涂色有2个，总个数是涂色的4倍，8÷2=4。

生2：涂色有1个，空白个数是涂色的7倍，7÷1=7;也可以说，涂色有1个，总个数是涂色的8倍，8÷1=8。

生3：涂色有4个，空白个数是涂色的1倍，4÷4=1;也可以说，涂色有4个，总个数是涂色的2倍，8÷4=2。

接着，教师让学生一起讨论生2的表征情况：算式中每个数表示的意思，并说说为什么有7倍和8倍的区别，让学生明白标准量都是1个，比较量不一样，它们之间的关系就不一样，也就是倍数不一样，使学生进一步懂得标准量相同时，可以从不同的角度来比较与观察，从而得到不同的结果。

随后，教师设疑：

师：刚才大家涂色时涂了1个、2个、4个，怎么没有涂3个呢？

生4：因为涂3个，空白是5个，它们之间没有倍数了。

生5：涂3个，总数8个，8不能除以3。

师（出示图2）：其实，5个和3个、8个和3个之间有倍数关系，它们是1倍多一些和2倍多一些，只是现在还没有学到这个知识点。

这一环节主要让学生了解虽然两个数之间除不尽，但它们之间仍然存在着倍数关系，为以后学习分数（小数）倍埋下伏笔。

随即，教师针对生3的表征结果设问。

师：这里还可以找到不一样的倍的关系吗？

生6：空白有4个，涂色个数是空白的1倍，总个数是空白的2倍。

师：同样是1倍，有不一样吗？

生7：刚才空白个数是涂色的1倍，标准量是涂色个数，现在涂色个数是空白的1倍，标准量是空白个数，虽然都是1倍，但标准量和比较量发生了变化，它们所表示的意义是不一样的。

复习时，教师必须让每个学生能从原有认知结构中迅速、正确地回忆起知识，促使其大脑兴奋，从而能主动、高效地参与课堂。这一环节主要有三个部分，每部分环环相扣、层层递进，不仅引导学生从部分与部分的角度去观察它们之间的关系，而且给予解决问题的脚手架，引导其从部分与整体的角度去寻找它们的关系，更明确了：如果标准量与比较量发生变化，所表示倍的意义也随之发生变化。当然，教师在教学中发现，学生容易表示出空白个数与涂色部分的倍数关系，而表示总个数与涂色部分的倍数关系时存在一定思维障碍。我们以为，这与教材的编排有一定的关系，这一单元中没有安排“整体与部分之间的倍数关系”的相关例题或习题，可能造成教师在教学时有所疏忽。因此，从这个意义上说，基于关系的倍的复习是必要的。

（二）多维观察，深刻理解量与量的关系

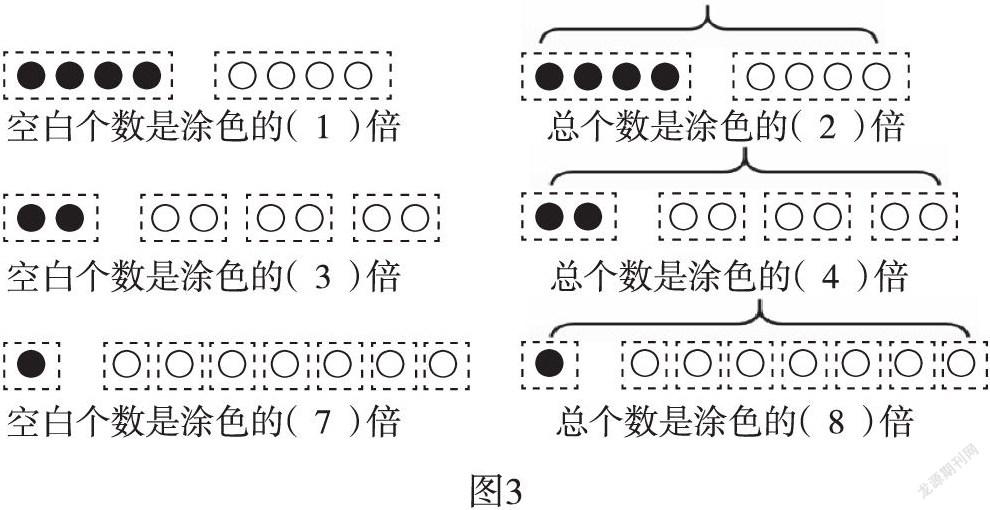
在第一环节的基础上，逐渐梳理出完整的关系图（如图3），教师组织学生观察左右两列的异同点。有了上述基础，学生在同桌交流的基础上很快梳理出内在的关系。

生1：左边都是空白部分与涂色部分之间的倍数关系，右边是总数与涂色部分之间的倍数关系。

生2：它们的标准量是一样的，都是涂色个数，而比较量是不一样的。

生3：左边与右边横着看，发现右边比左边的分别多1倍。

生4：右边的比左边的多1倍，这个1倍就是涂色部分本身的1倍。

师：通过比较可以清晰发现，左边是部分量与部分量之间的关系，右边是整体量与部分量之间的倍数关系，整体与部分量之间多的1倍就是标准量自身的1倍。

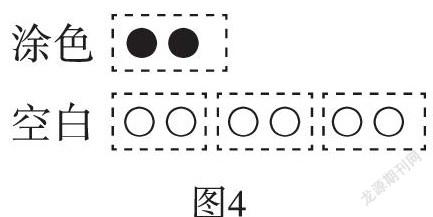
师：现在把其中一种关系变一下（如图4），大家还能发现这里的倍数关系吗？

生5：空白个数是涂色的3倍，算式是6÷2=3。

生6：总个数是涂色的4倍，算式是8÷2=4。

生7：空白个数比涂色多的个数是涂色的2倍，算式是（6-2）÷2=2。

师：这里的3倍、4倍、2倍分别表示什么意思呢？

…………

接著，教师组织学生观察图5中这三个图示之间的区别。经过讨论，学生一致认为前两幅图是部分与部分之间的倍数关系，第二个图示的比较量是两个量之间的差异量，第三个图示是部分与总体之间的倍数关系，通过这一观察、比较与分析，揭示了本节课核心主题是借助于倍的复习来研究数量之间的关系。

我们认为，这一教学环节中的亮点是把原始直纸条表征的方法转变到更清楚的上下对比的表征方式，通过对直观几何图形的不同角度观察和变化，使部分与整体（部分）之间的关系更加清晰，为后续学习和倍关系、差倍关系，甚至是“比”等关系起到较好的铺垫作用，在思维层次上也提升了一个台阶。

（三）多型练习，建构不同倍的模型

在进一步掌握倍的意义的基础上，明确了量与量之间的倍数关系可以是部分与整体的关系，也可以是部分与部分的关系，甚至可以是部分与两个量之间相差部分的关系。

随即，教师出示三个不同类型的题目（如图6），要求学生根据图示的意义独立编题，四人小组交流后集体反馈，让学生能从自己的生活经验入手，编制一些不同情境、不同类型的题目，使学生对倍的意义和关系理解更为深刻，从而建立起解决倍问题的数学模型。

笔者以为，三个题目类型不同、目标不同、层次不同，较好地体现了复习课面向全体又有差异的特征。第一题已知标准量和倍数，求比较量，指向于复习巩固;第二题已知倍数关系和总数，求标准量，指向于用算术的思维解决和倍关系中的一倍数;第三题是已知比较量与标准量之间的差异量和倍数，求标准量，指向于用算术的思维解决差倍关系中的一倍数。这一环节是在“一题”的基础上变化抽象而来的，更加符合数学的本质属性，更有思维含量，更能促进高阶思维的发展。

郑毓信教授认为，数学基础知识不应求全，而应求联。我们巧设“一题”，构建起以“关系”为主题的倍的复习，对所学知识进行系统整理，着力做到知识的“联”，厘清了倍知识的“前世今生”与后续走向，充分发挥了“一题”的功能，使知识“活”起来，让思维“动”起来，令能力“长”起来，不断发展学生的高阶思维。