输入测点误差对结构振声预报影响的实验研究*

王 霂，王洪波

（海军士官学校 六系，安徽 蚌埠233012）

目前对结构振动辐射声场的研究中，研究者们习惯将动力信息作为数值模拟计算的输入载荷[1-3]。然而，在实际工程中，结构所受到的激振力往往很难测得。虽然理论上在激振力的传递路径上安装力传感器可以测得相当精度的激振力，但实际中，机器设备的动力传递路径上一般并没有足够的空间去安装力传感器。而且，力传感器一般不能承受较大的横载，如将其安装在机器设备的动力传递路径上，总会降低轴系的各项性能，从而难以获得准确的激振力数据。因此，通常情况下，机器设备所受的激振力难以通过力传感器直接进行测量。

对于这一问题，通常的解决办法是在激振力作用点或附近安装加速度传感器采集振动加速度信号，经过处理后作为输入载荷。由于加速度传感器的尺寸远远小于力传感器，且不需要侵入机器设备的动力传递路径进行安装，这种方法应用相当普遍。采集到加速度信息后，采用大质量法[4-5]进行信息处理并作为载荷输入，已被证明是一种相当有效的方法[6-8]。然而，这种方法并不能解决所有问题[9]。以某型水泵为例，其轴力作用在一个内部的充水空间中，激振力作用点及附近连加速度传感器的安装都十分困难。此外，在实际操作中，由于各种因素影响，也很难保证加速度传感器安装位置恰好就是激振力作用点。针对类似情况，彭旭、骆东平提出根据设备基座振动加速度测试数据频谱曲线，求出不同频率下的加速度，再由设备的质量求出等效的惯性力作为输入载荷效的惯性力作为输入载荷[10]，并据此进行了水下振动和噪声预报。纪刚、周其斗等对此方法进行了较为详细的介绍，在已知激振点的情况下，采用大阻抗法，以基座振动数据作为输入，准确预报了水下结构振动与噪声辐射[11]。

然而，实际工程测量中，不仅激振数据较难获取，精确测定激振点位置也十分困难。通常，只能确定激振作用的一小片区域。因此，能否通过选取激振力作用点附近乃至较远处测点作为激振点，使用所测得的加速度信息作为输入载荷，进而给出准确的数值模拟结果是一个值得探讨的问题。目前，关于输入载荷测点选取误差对结构振动及声辐射预报的影响，国内外均未见研究。

本文首先利用舱段模型实验结果对大质量法的准确性进行了验证。之后将实验测得的距离真实激振点位置不同的测点处加速度信息分别作为输入载荷，利用大质量法对模型的振动及辐射声场进行了数值模拟，并与实验所测的振动与辐射声场信息进行了对比。最后，在此基础上，对激振加速度测点选取对结构振动及辐射声场影响的规律进行了定性研究，给出了输入载荷测点误差的工程允许范围。

1 大质量法的验证

1.1 实验模型和测点分布

实验所使用的舱段模型为内部有激振平台基座的加肋带盖圆柱壳，其外形如图1 所示，激振机安装在模型内部的激振平台基座上，通过激振基座面板来激起整个舱段模型的振动。

模型的相关几何参数如表1 所列。

图1 实验舱段模型

实验中模型表面测点如图1 所示，测点A-I 分别为1-9 号肋骨位在模型表面的对应位置。测点J、K、L 为图1 下方安装传感器的测点，是模型内部基座支脚在表面上的对应位置。除图1 中已标出的测点外，测点O 位于模型端盖中心处。

内部测点N1-N8 分布在以激振点为中心，边长为100mm 的正方形上，如图2 所示。测点0 恰好位于激振点处。

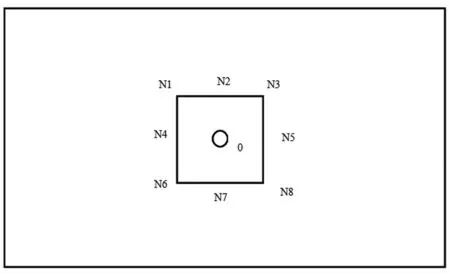
图2 激振机基座上加速度测点分布示意图（俯视）

1.2 计算模型和方法概述

根据实验舱段模型的几何参数和实际状态，在PATRAN 中建立有限元计算模型。采用Tria3 三角形单元对模型表面进行划分，Quad4 四边形单元对基座进行划分，单元尺度为50mm。模型共划分为7194 个节点，13247 个单元，如图3 所示。

图3 计算使用模型及单元划分

边界元的划分与模型湿表面的有限元划分相同。

以激振点处实测加速度作为计算模型的输入载荷，约束状态选取为自由状态。声学边界条件方面，以地面作为声学硬反射边界条件，模型中心距离地面高度与实测值相同，为1420mm。

使用大质量法计算时，根据文献[4]的建议，在模型上激振力作用点处附加1×106t 的大质量（模型自重约为1t），以实测加速度时域信号傅氏分解在该激振频率下的幅值乘以大质量作为载荷输入，采用结构有限元耦合流体边界元（FEM/BEM）计算方法[12-14]，计算模型结构流固耦合振动及空气辐射声场。

图4 测点D 计算结果与实测结果对照

图5 测点E 计算结果与实测结果对照

1.3 大质量法计算舱段模型受激振动

以舱段外表面上测点D、E 的法向实测振动加速度级作为参考，大质量法数值模拟结果与实验结果对比如图4、图5。

计算结果表明，在已知激振点位置的情况下，采用激振力信息输入和激振加速度信息输入均能取得较好的计算结果，数值模拟结果与实验测量结果相差均不超过6dB。除个别频率外，绝大多数频率上数值模拟的误差不超过3dB。在工程范围上，可以认为数值模拟结果是相当准确的。由此可以得知，在已知激振点位置的情况下，使用激振加速度信息，采用大质量法能够近似准确预报结构受激振动情况。

1.4 大质量法计算舱段模型空气辐射声场

在激振机有效工作频率内，对空气中舱段模型辐射声场进行数值模拟。以距离地面1200mm、距离模型中心2500mm 的声场点为例，模型端盖外侧和舱壁中心外侧声场点辐射声压随激振频率的变化数值模拟结果与实验结果对比如图6、图7。

图6 端盖外侧声场点数值模拟结果与实验结果对比（距地面1200mm）

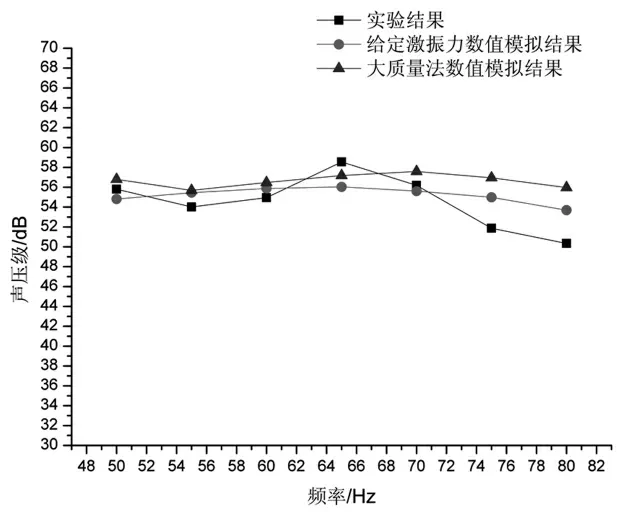
图7 舱壁外侧声场点数值模拟结果与实验结果对比（距地面1200mm）

可以看到，大质量法数值模拟结果与给定实测激振力的数值模拟结果基本相同，并且与实验结果间的变化规律基本一致。在数值上，两种数值模拟结果和实验结果非常接近。大部分情况下三者之间的误差小于3dB，最大误差也不超过7dB。

近场声指向性方面，60Hz 时，在距离地面高度1200mm 的平面内，声场指向性的两种数值方法模拟结果和实验结果的对比如图8 所示。

从图8 中可以看出，在声指向性上，利用激振点加速度信息采用大质量法进行数值模拟的结果与直接给定激振力数值模拟结果基本相同，与实验结果有相似的规律，绝大多数测点声压级数值误差在3dB 以下，最大误差不超过7dB。这说明，大质量法数值模拟能准确预报空气中结构受激振动辐射声场指向性。

本节的计算比较说明，大质量法数值模拟结果能准确预报空气中含有硬反射边界条件的结构流固耦合振动及其辐射声场，误差范围一般不超过3dB，最大不超过7dB。这一精度在工程上是完全可以被接受的。

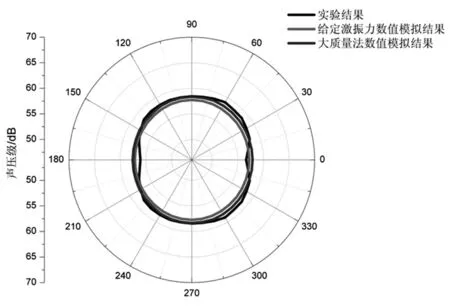
图8 60Hz 时空气声场指向性数值模拟结果与实验结果对比（距地面1200mm）

图9 使用非激振点加速度作为输入载荷对结构受激振动的影响（D 点）

图10 使用非激振点加速度作为输入载荷对结构受激振动的影响（E 点）

2 输入载荷选取对振动计算的影响

按照测点与激振点之间的距离变化，分别在模型内部基座上N2、N1 点和表面K、E、O 点处附加大质量，使用大质量法进行数值模拟。使用不同测点实测加速度作为载荷，应用大质量法得到表面D、E 点处的振动加速度幅值与实测值的比较见图9、图10。

所选取的五个测点中，测点N2 和N1 点与激振点的距离较近，分别为基座面板上振动波长的9%和12.7%；测点K、E、O 与激振点较远，均超过了一个振动波波长。

当使用距离激振点较近的N2 点或N1 点的实测加速度作为输入载荷时，计算误差处于可以接受的范围，最大不超过7dB。使用距离激振点更近的N2 点的实测加速度作为输入载荷，其计算误差相比使用N1 点实测加速度作为输入载荷要小大约3dB。

使用距离激振点较远处的K 点或O 点的实测加速度作为输入载荷时，数值计算无法得到准确的计算结果，甚至无法预报振动变化趋势。此外，注意到采用E 点的实测加速度作为输入载荷时，在E 点自身能准确预报其振动，但是，在与其距离并不远的D 点处，所预报的振动最大误差超过20dB。实际上，采用E 点的实测加速度作为输入载荷时，并不能准确预报结构的受激振动。使用非激振点实测加速度作为输入载荷时，能算准该点自身的振动情况，是因为其自身的振动信息实际上是作为数值模拟的边界条件而被给定，与计算准确性无关。

这一结果很好理解，当所选取的测点与激振点越接近时，数值模拟越能够反映真实情况，从而误差越小；反之，数值模拟的状态与真实状态相差越远，误差越大。

3 输入载荷选取对空气辐射声场计算的影响

3.1 声场传递函数分析

随着选取的测点变化，距离地面1200mm、距离模型中心2500mm 的声场点处，模型端盖外侧和舱壁中心外侧声场点辐射声压随激振频率的变化数值模拟结果与实验结果对比如图11、图12。

图11 端盖外侧声场点数值模拟结果与实验结果对比（距地面1200mm）

图12 舱壁外侧声场点数值模拟结果与实验结果对比（距地面1200mm）

计算结果表明，使用距离激振点较近的N2 点或N1点的实测加速度作为输入载荷时，对空气中结构受激振动辐射声场的数值预报误差不超过8dB。使用距离激振点更近的N2 点的实测加速度作为输入载荷，其计算误差相比使用N1 点实测加速度作为输入载荷要小大约2dB。

当加速度测点偏移较大时，数值模拟结果与实验结果相差甚远，无法预报空气中结构受激振动辐射声场。

3.2 声场指向性分析

仍在N2、N1、K、E、O 点处附加大质量，使用大质量法进行数值模拟。随着测点改变，距离地面1200mm、距离模型中心2500mm 的声场指向性数值模拟结果与实验结果对比如图13 所示。

与声场传递函数结论相同，当加速度测点与激振力作用点较近时，数值模拟的声场指向性与实验结果相符较好，误差随加速度测点偏移量增加而增大；当加速度测点与激振力作用点较远时，数值模拟的声场指向性与实验结果偏差超过20dB，指向性趋势也不尽相同，无法预报空气中辐射声场指向性。

4 分析和讨论

本文的工作表明，当加速度测点与激振力作用点相距不太远时，采集的加速度信息可以作为输入载荷用以近似预报结构受激振动及其空气中辐射声场，计算误差随加速度测点偏移量增加而增大；当加速度测点与激振力作用点相距较远时，其所采集的加速度信息作为输入载荷时无法准确预报结构受激振动及其空气中辐射声场。

对工程应用而言，需要振动加速度级和空气辐射声场的数值预报误差不超过5-8dB。本实验中，使用测点N1 处的实测加速度作为输入载荷进行数值模拟，所得结果与实验量测结果的误差恰为工程允许误差的上限。不失一般性，并考虑到一定的工程裕量要求，当无法准确获得激振力信息和实际激振点位置时，若实际加速度测点位置与激振点位置相差不超过振动波长的10%时，可直接采用该测点测得的加速度信息作为输入载荷，通过大质量法进行数值模拟，得到工程范围内误差允许的结构振动加速度和空气辐射声场信息。

如上所述，如采用大质量法进行数值模拟，在无法获取较小的激振力作用点范围时，将很难得到准确的振动与辐射声场预报结果。一种可能可行的方法是，根据实测的多点加速度信息与预估位置单位力激振下的数值模拟结果进行拟合，近似求得激振力信息，并以此作为数值模拟的输入载荷，从而近似预报结构受激振动及其空气中辐射声场。

图13 60Hz 时空气声场指向性数值模拟结果与实验结果对比（距地面1200mm）