融入运动信息和模型自适应的相关滤波跟踪
2021-01-11陈永安张少帅王会峰
黄 鹤,陈永安,张少帅,茹 锋,王会峰,郭 璐
(1.长安大学电子与控制工程学院,陕西 西安 710064;2.无人机系统国家工程研究中心,陕西 西安 710072)
0 引言
视觉目标跟踪是计算机视觉领域的热点问题,在视频监控、机器人和无人驾驶等领域都有着广泛的应用前景[1-3]。跟踪问题的任务,是根据给定目标的初始位置去估计目标在图像序列的轨迹[4]。
近年来,基于检测的跟踪方法显示出良好的跟踪性能,这类方法将目标跟踪任务作为一个分类问题来处理,利用目标和背景的图像块在线训练分类器[5]。其中,相关滤波器速度快效果好,成为当前的主流研究[6-13]方向之一。
边界效应是相关滤波类算法自引入循环矩阵的固有缺陷,一直未被解决,当前主流算法多采用在叠加余弦窗去缓解,但余弦窗却带来了新的问题。因此,针对跟踪场景中常见的目标遮挡问题,本文提出了一种融入运动信息和模型自适应的相关滤波跟踪算法,用来处理余弦窗的影响和复杂场景中目标遮挡的难题,在保证实时性的情况下,有效提升跟踪算法的精确度和成功率。
1 跟踪算法
1.1 多特征融合
众所周知,HOG特征对运动模糊和光照变化具有很强的鲁棒性,但对快速变形和快速运动目标跟踪效果不好;颜色直方图对变形不敏感,但对光照变化和背景颜色相似跟踪效果不好。因此,本文算法采用模板类特征HOG与统计特征颜色直方图互补线性结合框架,具体细节参考文献[12],即
f(x)=γtmplftmpl(x)+γhistfhist(x)
(1)
ftmpl(x)为模板响应;fhist(x)为颜色直方图响应;γ为融合系数。将式(1)分为两部分进行求解。
模板响应是K通道特征图像的一个线性函数
ftmpl(x;h)=∑u∈Th[u]Τφx[u]
(2)
φx为图像模板特征;φx:T→RK,定义在有限的网格T⊆Z2;h为模板模型参数。
直方图响应由m通道特征图像中计算得到
fhist(x;β)=g(ψx;β)
(3)
(4)
ψx为图像颜色直方图特征;ψx:H→Rm,定义在有限的网格H⊆Z2;β为颜色模型参数。
使用2个岭回归方程得到参数h和β的解
(5)
(6)
Lhist(β;ψ)为颜色直方图的损失函数;λ为正则项系数。
模板参数h及其在线更新为:
(7)
(8)
(9)

颜色直方图参数β及在线更新为:
(10)
ρt(O)=(1-ηhist)ρt-1(O)+ηhistρt(O)
(11)
ρt(B)=(1-ηhist)ρt-1(B)+ηhistρt(B)
(12)
ρt(O)和ρt(B)由颜色统计特征得到;ηhist为颜色特征学习率。
1.2 余弦窗影响处理方法
本文在叠加余弦窗的基础上,引入卡尔曼滤波和上下文感知滤波器[14],减缓余弦窗的影响。
1.2.1 卡尔曼滤波
相关滤波类算法都是以上一帧目标位置为中心进行搜索检测。当遇到目标快速运动,目标移动到搜索区域边缘,部分目标像素会被余弦窗过滤掉,此时无法保证得到的响应全局最大,造成跟踪结果变差;或者部分目标已经移出了搜索区域,此时余弦窗会过滤掉仅存的目标像素,造成跟踪失败。因此算法引入卡尔曼滤波,预测当前帧目标的位置,以预测位置为中心进行搜索检测。
采用线性等速模型来近似目标帧间位移,目标的状态建模为Et=[u,v,u′,v′],u和v分别代表目标中心的水平和垂直像素位置;u′和v′分别代表水平和垂直速度分量。
(13)
(14)
(15)
(16)
(17)


目标的观测状态Zt通过模板响应和直方图响应的线性融合得到。对公式中P0、Q和R的取值分析:P0代表对初值估计的不确定性,初值由标注数据给出,故取P0为零矩阵。目标观测状态Zt由滤波算法获得,可信度较高,目标预测状态只是近似估计,可信度较低,故在数值上R≪Q,这里取Q=10I(4),R=0.1I(2),I为单位阵。
1.2.2 上下文感知滤波器
由于余弦窗过滤掉分类器需要学习的背景信息,当目标遇到复杂背景干扰时,容易造成跟踪失败。引入上下文感知滤波器,作为部件添加到相关滤波器中,该方法提取目标框上下左右4块背景信息,对相关滤波器进行训练,并且还有破坏模型的封闭解。加入目标周围背景信息后,相当于把式(5)的求解变为
(18)
A0代表目标框;Ai代表目标周围背景块,与式(5)相比,多了λ3正则项。
式(18)整理为
(19)
f(h,B)为凸函数,将梯度设置为0,使其最小化,得到
(20)
在傅里叶域上得到封闭解为
(21)
1.3 模型自适应更新
相关滤波类跟踪算法采用固定的更新率,每一帧都更新模型参数,这种更新策略有很大的缺陷。采用每一帧都更新的模式,当目标遇到连续遮挡时,模型持续更新,会学习到大量干扰信息,造成跟踪漂移。采用固定更新率,如果更新率设置过大,且遇到遮挡、模糊、背景杂波时,模型会快速学习到大量干扰信息;如果更新率设置过小,则模型的更新速度赶不上目标的变化程度。
在此,引入高置信度检测方法[15],根据2个准则去判断是否更新
Fmax=maxF(s,y,w)
(22)
(23)
F(s,y,w)表示模板响应图;Fmax、Fmin和Fw,h分别表示响应图中最大值、最小值和w行h列元素。平均相关峰值能量EAPCE表示响应图的波动程度和检测目标的置信度。
当前帧EAPCE和Fmax的值大于历史平均值α1和α2倍时才进行模型更新。在模型更新时,提出一种新的自适应学习率方法
(24)
(25)

2 实验与结果分析
为了验证和评估本文算法,将本文算法与当前6个主流相关滤波类算法DSST[5]、KCF[9]、fDSST[10]、Staple[12]、Staple-CA[15]、SAMF[16]进行了对比实验,采用OTB-2015[17]作为实验数据集。
2.1 评价指标
评价标准采用精确度和成功率2个指标。精确度指中心位置误差(center location error, CLE)小于某一阈值的帧数占总帧数的比值。中心位置误差计算式为
(26)
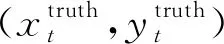
成功率指重叠率(overlap rate, OR)大于某阈值的帧数占总帧数的比值,实际上成功率评分时采用这个曲线下方的面积。重叠率的计算式为
(27)
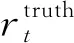
2.2 实验环境及参数设置
实验环境为Windows10操作系统,MATLAB 2018a,CPU为I7-8700HQ,RAM为16 GB。模板分类器的学习率ηtmpl_b=0.02,线性融合系数γtmpl=0.8。直方图分类器的学习率ηtmpl_b=0.04,融合系数γhist=0.2。正则权重λ1=1/3,λ2=1/3,λ3=0.5。模型自适应更新中,α1=0.4,α2=0.5,α3=1.3。
2.3 实验评估
2.3.1 总体性能比较
为了对比算法总体性能,将本文算法与其他6个主流算法在OTB-2015数据集上比较,实验表明本文算法精确度和成功率分别为0.821和0.615,比Staple-CA算法在精确度上提升了1.3%,成功率上提升了2.8%;比Staple算法在准确度上提升了4.7%,成功率上提升了6.2%。本文算法运行速度为54.34帧/s,与其他几种算法相比,本文算法在成功率和精确度得到提升的同时,速度上仍满足实时性。几种算法精确度和成功率具体对比结果如图1和图2所示。算法速度对比结果如表1所示。

图1 精确度曲线
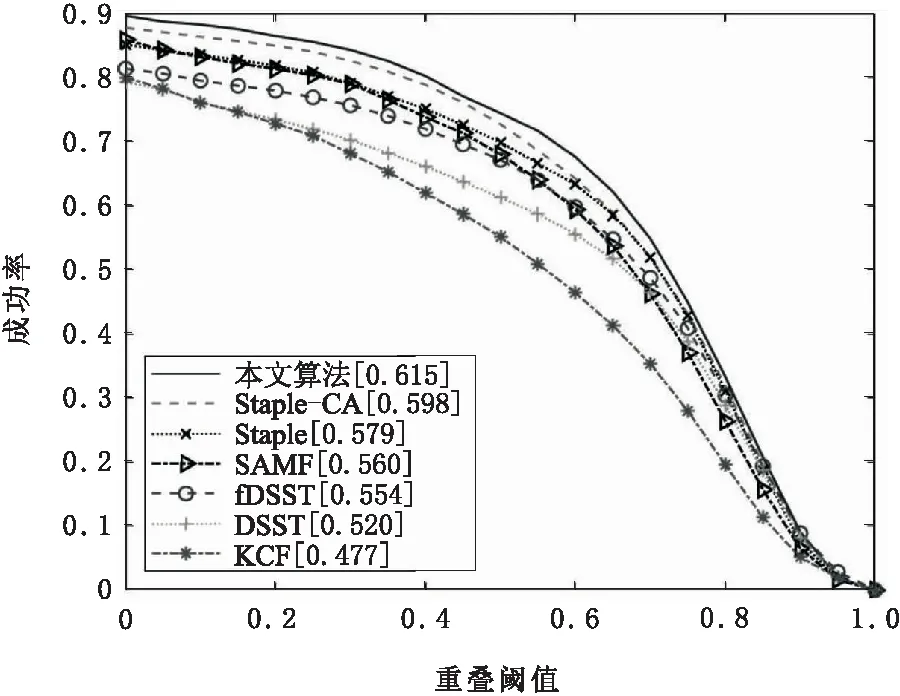
图2 成功率曲线

表1 跟踪算法平均速度 帧·s-1
2.3.2 数据集属性分析
为了充分评估本文算法在复杂场景中的性能,根据OTB-2015数据集提供的11种标注属性,对比本文算法与其他6种算法在11种属性上的成功率,具体结果如表2所示。
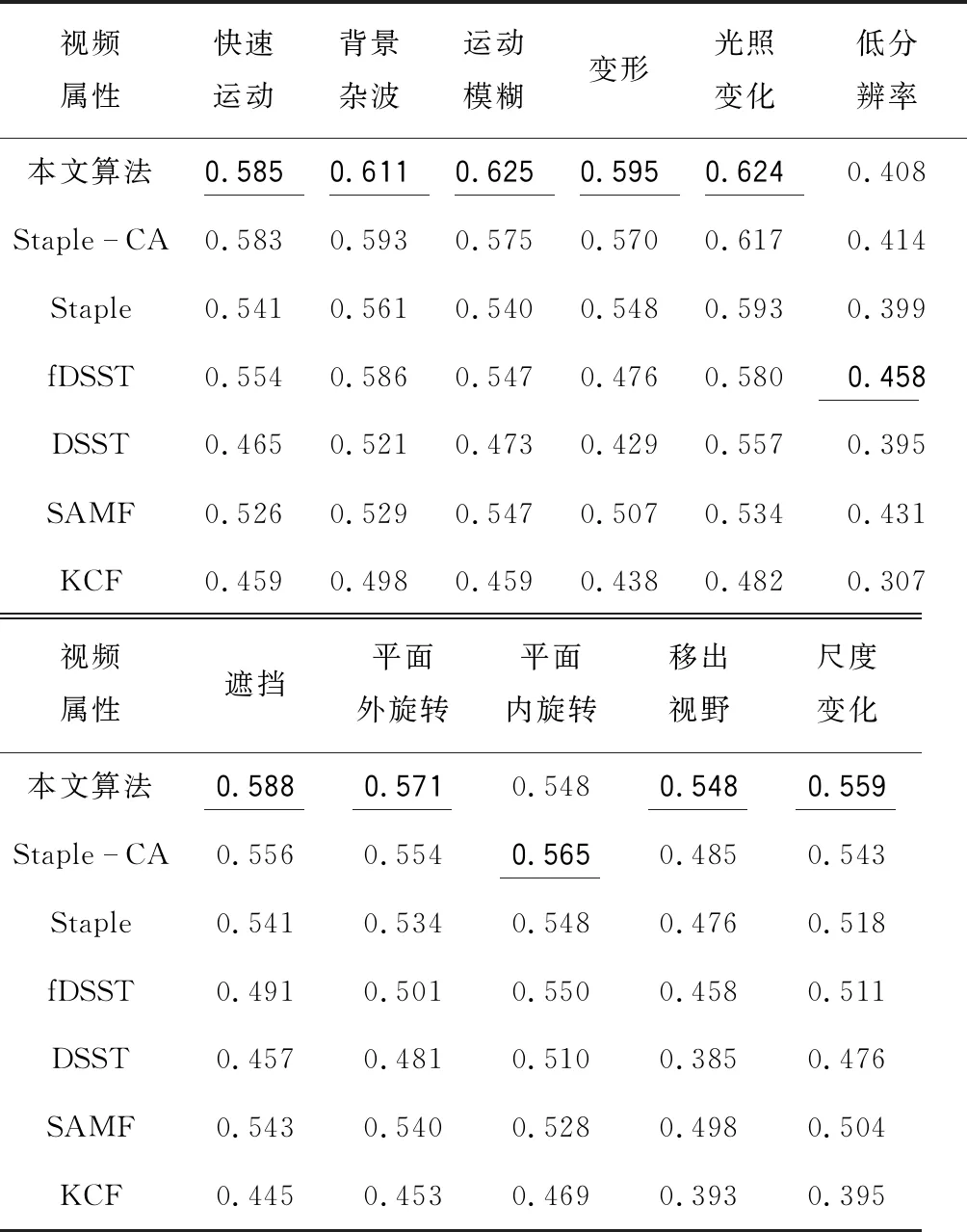
表2 各个算法在11种属性上的成功率
在表2中,黑体加下划线为该属性的最优值,本文算法在成功率上9个属性最优。与Staple-CA算法相比,本文算法在背景杂波,运动模糊,变形,遮挡,平面外旋转,移出视野,尺度变化7个属性上成功率提升显著,分别提升了3.0%,8.7%,4.4%,5.8%,3.0%,13.0%和3.0%。
2.3.3 跟踪结果比较
为了更直观地对比分析算法的跟踪性能,将本文算法与图2中排名靠前的Staple-CA和Staple算法在视频序列中的girl、jogging、skiing、couple进行定性分析。图3为3种算法在测试序列的部分跟踪结果。
在图3的girl序列、jogging序列中,当目标遇到连续严重遮挡时,其他几种算法仍持续更新模型,学习到大量干扰信息,造成后续帧全部跟踪失败。而本文算法加入模型自适应更新,有较强的抗遮挡能力,对大部分遮挡序列都能较好跟踪。在skiing序列中,由于目标快速运动,目标移动到搜索区域边缘被余弦窗过滤掉,从而造成跟踪失败。在couple序列中,目标周围有较多背景杂波,其他算法在跟踪时,采用固定学习率每一帧都更新模型,致使滤波器学习到大量背景信息,造成跟踪漂移。而本文算法采用自适应学习率,从而受到影响较小。

图3 3种算法在4个视频序列上的跟踪结果
3 结束语
本文提出一种融入运动信息和模型自适应更新的相关滤波跟踪算法,引入卡尔曼滤波和上下文感知滤波器,有效解决了余弦窗的影响;引入高置信度检测方法和一种自适应学习率方法,有效解决了目标遮挡问题。将本文算法与其他6种主流算法在OTB-2015数据集上进行对比实验,结果表明:本文算法精确度和成功率分别为0.821和0.615,比Staple-CA算法精确度提升了1.3%,成功率提升了2.8%,相比其他算法跟踪效果提升明显,鲁棒性较强。同时,本文算法速度为54.34 帧/s,满足实际工程实时性要求。
