Species abundance distribution models of Toona ciliata communities in Hubei Province, China

Yang Wang · Huoming Zhou · Jingyong Cai ·Congwen Song · Linzhao Shi

Abstract The study of plant species abundance distribution (SAD) in natural communities is of considerable importance to understand the processes and ecological rules of community assembly. With the distribution of tree, shrub and herb layers of eight natural communities of Toona ciliata as research targets, three different ecological niche models were used: broken stick model, overlapping niche model and niche preemption model, as well as three statistical models:log-series distribution model, log-normal distribution model and Weibull distribution model, to fit SAD of the different vegetation layers based on data collected. Goodness-of-f it was compared with Chi square test, Kolmogorov-Smirnov(K-S) test and Akaike Information Criterion (AIC). The results show: (1) based on the criteria of the lowest AIC value, Chi square value and K-S value with no significant difference (p> 0.05) between theoretic and observed SADs.The suitability and goodness-of-f it of the broken stick model was the best of three ecological niche models. The log-series distribution model did not accept the fitted results of most vegetation layers and had the lowest goodness-of-f it. The Weibull distribution model had the best goodness-of-f it for SADs. Overall, the statistical SADs performed better than the ecological ones. (2) T. ciliata was the dominant species in all the communities; species richness and diversity of herbs were the highest of the vegetation layers, while the diversities of the tree layers were slightly higher than the shrub layers; there were fewer common species and more rare species in the eight communities. The herb layers had the highest community evenness, followed by the shrub and the tree layers. Due to the complexity and habitat diversity of the different T. ciliata communities, comprehensive analyses of a variety of SADs and tests for optimal models together with management, are practical steps to enhance understanding of ecological processes and mechanisms of T. ciliata communities, to detect disturbances, and to facilitate biodiversity and species conservation.

Keywords Toona ciliata community · Tree-shrubherb layers · Niche models · Statistical models · Species abundance distribution(SAD) · Model fit

Introduction

Species abundance distribution (SAD), the basic description of species mix in a community, is the foundation of species diversity research. SAD represents an important complementary method with which to explain the processes of plant community assembly (McGill et al. 2007; Ulrich et al.2016) on temporal and spatial scales. It has significance for understanding the mechanisms of species diversity formation and ecosystem maintenance (Borda-de-Água et al.2012) and forest functioning under current and future events of disturbance (Chazdon 2017; Holl 2017). Since the 1930s,research on SAD has gradually developed into an importance approach to explain community structure and species regional distribution rules (Ma 2003). A variety of statistical models, such as the logarithmic series model (Fisher et al. 1943), the lognormal model (Preston 1948), the negative binomial distribution model (Kempton 1979; Ma et al.1997), and the Weibull statistic model (Wu and Hong 1997;Qin et al. 2009) have been used to explain the mechanism of species abundance distribution in a community assembly.With increasing importance attached to ecology principles in SAD, models based on ecological interpretations such as the broken stick model (BSM) (MacArthur 1957), the overlapping niche model (ONM), the niche preemption model(NPM) (Whittaker 1972; Pielou 1975) and the neutral theory model (Hubbell 2001) have been widely used.

Contemporary computer science has facilitated the integration of ecological principles into mathematical statistics science and the proposal of SAD models with ecological significance (Tokeshi 1993). The parameters generated in each particular species abundance distribution model are provided by temporal and spatial abundance distributions, and these models can then explain the space resource distribution between habitats (Matthews and Whittaker 2015). This cannot be attained by any single species diversity research method (Magurran 1988). Changes in SAD, which describe variations in the number of individuals of species within a given ecological community (McGill et al. 2007; Alroy 2015), can def ine the structural complexity of the community available as a habitat for biodiversity, and may alter the relative contribution of each species to the forest function(Poorter et al. 2017; Ali et al. 2019). Therefore, SAD is more effective than species diversity indexes for understanding a community (Tokeshi 1993). Until recently, however, less focus has been placed on the utility of SAD in applied ecology and biodiversity management (Matthews and Whittaker 2015).

Toona ciliataRoem., a deciduous to semi-evergreen species, belongs to the genus Toona of the Meliaceae family. It has been listed as an endangered species under the secondary national protection of China (Yu 1999). The natural distribution ofT. ciliatahas been shrinking because of excessive consumption of its wood and the species poor natural regeneration.

Due to the varieties of mathematical and ecological meanings, each suitable model indicates the possible ecological process of a community (Ma 2003). Species abundance reflects a species ability to take up resources and allocate them to individuals (Kaspari 2001). The coexistence of species within a community can thus be explained by how species, with different resource needs and environmental requirements (water, nutrients, light availability), partition existing niches (Bispo et al. 2017; Villa et al. 2019). Therefore, niche widths and niche overlaps between species are considered the determinants of species diversities and community structures (Zhang 1995). We chose three ecological niche models as well as three statistical models to fit the species abundance distributions of tree, shrub and herb layers in eight naturalT. ciliatacommunities in Hubei Province. The three tests, namely Kolmogorov-Smirnov (K-S), Chi square(χ2) and Akaike Information Criterion (AIC), were used to compare the goodness-of-f it of the models. The optimal SAD models were ref ined with the expression of α diversity because a higher diversity is positive for the conservation of rare species (Reng et al. 2009) due to the balance between common and rare species (the maximized coexistence of common and rare species) in old-growth forests (Villa et al.2019). The changes of parameters generated in SADs can be adopted in the management and monitoring of community restoration (Villa et al. 2019). This is a more organized way of managing SADs in theT. ciliatacommunities. However,there are few studies evaluating SAD patterns for communities of endangered plants at a habitat scale. Based on the results of this study, more effective ecological practices and management measures could be designed to create satisfactory biodiversity conditions, and to monitor biodiversity with changes of SADs so as to conserveT. ciliataand its communities.

Materials and methods

Research areas

Hubei Province (108°21′-116°07′ E, 29°01′-33°16′ N) has high terrain in the west (mountainous areas), lower in the east (hilly areas) and lowest in the middle (Jianghan Plain),and has complex, varied habitats with diverse topographies,rich climates and soil conditions. Based on comprehensive and systematic field surveys of naturalT. ciliatacommunities in Hubei Province, eight natural communities in different geographical areas were selected (Table 1), basically covering the distribution of the species in the province.

Survey and sampling

The survey was conducted from 2015 to 2017. A 20 m × 20 m sample plot was established for eachT. ciliatacommunity, within which four 10 m × 10 m quadrates were located to survey tree layers. At four corners and the center of each plot, five 5 m × 5 m shrub quadrates and five 1 m × 1 m herb quadrates were located. There were 32 tree quadrates, 40 shrub quadrates and 40 herb quadrates in the eightT. ciliatacommunities. In each tree quadrate, species name, number, height, DBH and crown width were recorded.For shrubs and herbs, plant number, heights and coverage were recorded. Environmental conditions of the differentsites, such as soil types, aspects and so on, were recorded.We adopted the counted number of species for the fitting of SAD models.

Table 1 Location and environmental factors of eight T. ciliata communities in Hubei Province

SAD models and tests

Ecological niche models

1. BSM (broken stick model) is a resource allocation model of random ecological niches proposed by MacArthur(1957). The abundance niof theith species can be expressed as:

where S is the species number and N the total number of species in the community. They have the same meanings in the following.

2. ONM (overlapping niche model) was also proposed by MacArthur (1957). It is a resource allocation model but does not randomly assign each species to a niche. The model for proportional Picorresponding to the theoretical abundance is:

where Piindicates the proportion in accordance with the theoretical abundance.

3. NPM (niche preemption model) explains the species abundance distribution pattern according to the proportional partition of resources, where species abundance is equivalent to the proportion of the space occupied(Alroy 2015). The species number along the stick taken up by theith species abundance is (Whittaker 1972; Qin et al. 2009):

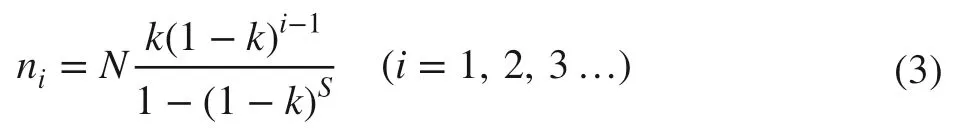
The undetermined parameter k value ranges between 0 and 1, and it can be solved with following formula with iteration:

where nminis the species number of the lowest species abundance in the community.

Statistical models

1. LSD (log-series distribution model) predicts the frequency of species with r individuals (Fisher et al. 1943;Ma et al. 1997) as follows:

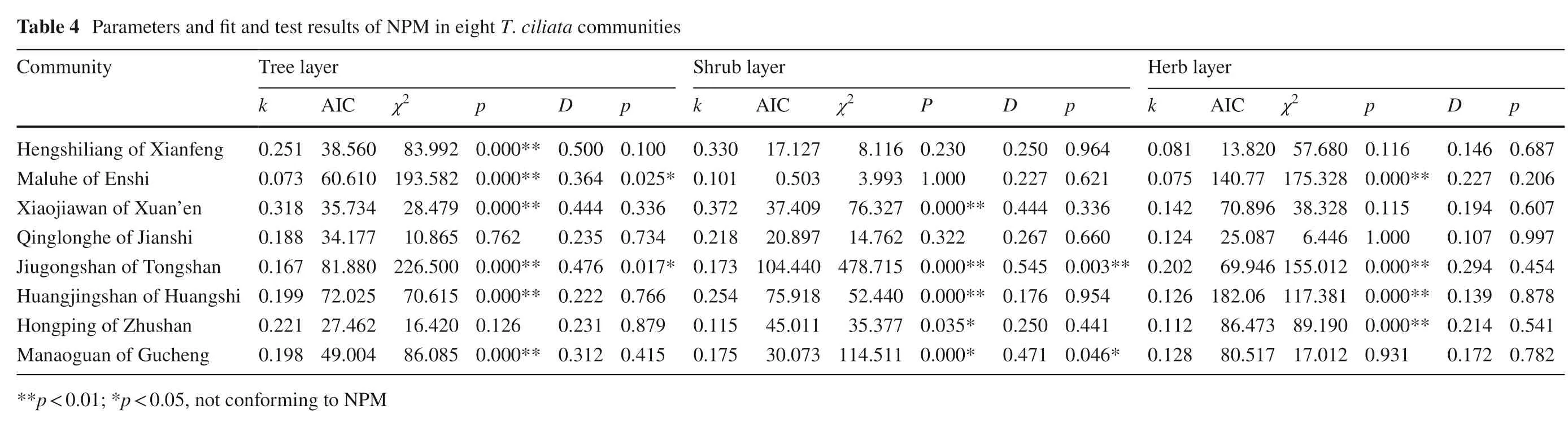
where α represents the characteristics of the community and can be used as the diversity index. Its value is greater than 0; x is a constant (0

2. LND (log-normal distribution model), truncated at the left end, was introduced by Preston (1948). In the order of community species abundance from the smallest to the largest, the octave method was used to group observed frequencies (Preston 1948; Qin et al. 2009).The formula of LND is:

where S (R) is the species number in the r th octave; S 0 represents the species in the octave with the largest species number. The λ, a reciprocal of the width of the normal distribution curve, is a parameter related to sampling size. The higher λ value indicates a thinner and higher curve, and a higher species density in the community (Gao et al. 2011).

3. WDM (Weibull distribution model) is expressed as:

where f (x) is the simulated frequency of species of x th degree, and the three parameters of WDM are: a, the position parameter; b, the scale parameter; c, the curve shape parameter (Wu and Hong 1997; Qin et al. 2009).We adopted the model with two parameters (b and c)with a as 0, and the maximum likelihood method was employed to solve b and c (Qin 2009; Qin et al. 2009 ).

Fitting tests for models

The six models were evaluated with the Kolmogorov-Smirnov (K-S) and Chi square (χ2) tests to verify goodness-of-fit. The probability p of testing significance was set at 0.01 and 0.05 to determine optimal models for each layer.

The Akaike Information Criterion (AIC) method was adopted to compare the models by a lower AIC value and by the goodness-of-f it of curves (Oksanen et al. 2019).

The AIC value could be used to select the optimal model but a model could not be rejected through the AIC value(Gao et al. 2011). The fitting model was selected with a relatively lower AIC value, a lower χ2and a lower K-S (p> 0.01,p> 0.05) as selection criteria. Data processing, statistics and model fit were completed using Excel 2007 and testing using the R language.

Results

Ecological niche models

The fit and test results with BSM of tree, shrub and herb layers in the eight communities are shown in Table 2. The χ2test rejected the BSM of seven tree layers (p< 0.01)but accepted the tree layer of the Gucheng community(AIC = 23.610, p of χ20.171, p of K-S 0.570). The χ2test accepted the BSM of the shrub layers (p> 0.05) of Xianfeng, Enshi, Jianshi, Zhushan and Gucheng communities and accepted the herb layers of Xianfeng, Jianshi and Gucheng communities. The BSM was better suited to the shrub layer of Jianshi (AIC = 20.871, p of χ20.881 and p of K-S 0.925),followed by the shrub layer of Enshi (AIC=−1.732, p of χ20.750 and p of K-S 0.215). The BSM was best suited to the herb layer of Jianshi community (AIC = 29.115, p of χ21.000 and p of K-S 0.907), followed by the herb layer of Gucheng community (AIC = 55.598, p of χ20.991 and p of K-S 0.782).

The fit and test results of the tree, shrub and herb layers with ONM revealed that the ONM could not explain the SADs of eight tree layers (p< 0.01), shrub layers (p< 0.01)of Xianfeng, Xuan’en, Tongshan and Huangshi, but could accept those of the shrub layers (p> 0.05) of Enshi, Jianshi and Gucheng; the χ2test only accepted SAD of the herb layer(p> 0.05) of Jianshi (Table 3).

According to the comparisons of K-S tests and AIC values, the shrub layer of Enshi (AIC = 7.096, p of χ20.977,p of K-S 0.621) had the highest goodness-of-f it, followed by the shrub layer of Gucheng (AIC = 31.983, p of χ20.925, p of K-S 0.954). The ONM best fitted the herb layer(AIC = 20.871, p of χ20.885, p of K-S 0.763) of Jianshi.The ONM analyses were consistent with the findings of the field surveys.

The fit and test results of niche preemption model (NPM)are shown in Table 4. The k value is related to the number of species in a community. A smaller k value indicates a greater number of species (Qin 2009) while a larger k shows the abundance of dominant species and the lower evenness of the community (Gao et al. 2011). Of the eight communities, Enshi community had the lowest k value of the tree layers with the largest number of species (33), while Xuanen had the highest k value with the smallest number of species (12). The lowest k values of shrub and herb layers were 0.101 and 0.075 respectively in Enshi community. NPM better fit the SAD patterns of the tree layer (AIC = 34.177,p of χ20.762, p of K-S 0.734) of Jianshi and could explain the goodness-of-f it of the shrub layers of Xianfeng, Enshi and Jianshi (p of χ2and K-S > 0.05), but Enshi shrub layer(AIC = 0.503,p of χ21.000,p of K-S 0.621) was optimal.NPM accepted the herb layers of Xianfeng, Xuan’en, Jianshi and Gucheng (p of χ2and p of K-S> 0.05), while the herb layer of Jianshi community (AIC = 25.087,p of χ21.000,p of K-S 0.997) was best fitted.

p D 0.146 0.687 0.107 0.90* 0.179 0.76 0.172 0.782 p 0.118 0.000*0.991.569 57 5.373 1.000.320 62 12 145.828 0.000** 0.258 0.2537 162.055 0.000** 0.294 0.454 Herb layer χ2 155.090 226.453 0.000** 0.333 0.037*3 AIC 127.440 123.690 123.715 0.000** 0.250 0.128.746.452 74 29 63.115.278.115 78 55.598 p*2 0.866 6 0.124 8 0.215 0 0.925 0.31 0.30 0.20 3 0.240 0.20 0.23 0** 0.59 5 0.734 0** 0.358 0.675 1 0.001*D 90 7 0.00 45 p 11.493 0.11 3 0.881 15.451 0.75 8.93 1.600** 0.55 3 0.00 5.396 0.00 χ2 52 1322.603 0.42 11 0.95 11.381 0.78 rovince Shrub layer AIC.524 13− 1.723 34.273 20.871.366 6** 94 73 38 24.895.133.073 ubei P 0764* 0.524 0.00* 0.500 0.10* 0.303 0.09* 0.444 0.33* 0.235 0.73 009 nities of H p mu D 0.308 0.57 in the eight T. ciliata com* 0.333 0.27* 0.250 0.69 p 0.000*0.000*0.000*0.171 107.595 0.000*.791.403.728 233.871 0.000*85 32 0.000*97.366 0.000*81 15 62.250.108 χ2 SM SM.460 35 68 34 23 73.193 AIC.452.618.536.636 shi 63 23 49.757.610 ing to B Fit and test results of BTree layer ianfeng uang Qinglonghe of Jianshi ot conform uanʹen ongshan f T nshi f H iliang of X ucheng f Z of X an Huangjingshan o Table 2 Hongping o unity hushan Hengsh Comm Maluhe of E Xiaojiaw Jiugongshan o uan of G Manaog** p< 0.01; * p< 0.05, n

p 8 0.249 17.540 196.464 0.000** 0.201 0.012*3 0.079 58.252 298.703 0.000** 0.32 125.93 296.216 0.000** 0.34 9 0.763 2 0.112 0.17 61.049 297.034 0.000** 0.419 0.009**0 0.345 167.30 566.587 0.000** 0.38 76.884 148.464 0.000** 0.251 0.367 D p Herb layerχ 2 AIC 20.871 17.749 0.885 79.706 59.879 0.000** 0.24 294 0** 0.375 0.627 143 0**p 0.227 0.62 7 0** 0.556 0.12 D 0.321 0.42 0.176 0.95 0.01 0 0** 0.636 0.00 911.714 0.00 0** 0.333 0.13 0.00 16.896 p 178.197 0.00 0** 0.412 0.11.318.689 b layer 263.113 0.00 9.482 0.97 0.17 5 χ2 17 558.720 0.92 Shru AIC.122 167.096.889 33 34.177.710* 91 78 43 31.573.726.983 munities p D p 6 0.000** 0.500 0.100 the eight T. ciliata com 9.77 5.428 0.000** 0.394 0.012*58.389 0.000** 0.556 0.124 33.757 0.004*0.235 0.734 8 0.000** 0.571 0.002*3.331 0.000** 0.444 0.057 6 0.000** 0.375 0.0211 0.22 3.20 34.590 14 NM ing to O in NM χ2 AIC Fit and test results of OTree layer 61.746 20 35.777 15.542 73.640 42 27.546 g 33.610 0.000** 0.385 0.291 48.666 12 ianfen f Tuangshi 63.711 17 nshi uanʹen iliang of X of X ongshan f Hshan unity Table 3 Hengsh Jiugongshan o Hongping of Z Xiaojiawan Huangjingshan ohu Qinglonghe of Jianshi ucheng uan of G Comm Maluhe of E Manaog** p< 0.01; * p< 0.05 not conform

p D 0.146 0.687 0.194 0.607 0.107 0.997 0.172 0.782 p.680 0.116 8 0.000** 0.227 0.206 6 1.000 2 0.000** 0.294 0.454 1 0.000** 0.139 0.878.190 0.000** 0.214 0.541 χ2 175.32 96 38.328 0.115* 0.202 69.946 155.01 0.081 13.820 57 0.142 70.8 17 17.012 0.931 117.38 layer AIC 0.77 2.06 Herb k 0.075 14 0.124 25.087 6.44 0.126 18 0.112 86.473 89 0.128 80.5 0 0.964 0.25 p 4 0.336 7 0.621 7 0.660 0.26 0.22 0** 0.545 0.003*0 0.441 D 6 0.954 0** 0.17 1 0.879 0.115 45.011 35.377 0.030 0 1 0.046*5 0.00 3.99 P 3 1.00 1 0.00 6 0.23 0** 0.44 14.762 0.322 8.11 8.71 0* 0.47 4.51 rub layer χ2 AIC.8970 47 5* 0.25 Sh k 0.1010.50 5 0.734 0.218 204.44 munities p eight T. ciliata com 0 0.100 0.330 17.1273 0** 0.504 0.025*0** 0.364 0.336 0.372 37.409 76.327 0.00 0.173 10 0** 0.44 2 0** 0.47 0.236 0.017*2 0.766 0.254 75.918 52.440 0.00 0.23 0** 0.22 6 0** 0.312 0.415 0.175 30.073 11 D p in 2 0.00 0 0.00 PM 3.58 6.50 f N χ2 fi t and test results o 60 83.992 0.00 AIC 0.251 38.510 19 0.073 60.634 28.479 0.00 0.318 35.7 80 22 shi 0.199 72.0 0.167 81.825 70.615 0.00 0.221 27.4 PM 62 16.420 0.12 ing to N04 86.085 0.00 0.198 49.0 Tree layer k 0.188 34.177 10.865 0.76 Parameters and ianfeng uang uan’en Qinglonghe of Jianshi ot conform f T ucheng nshi ongshan Maluhe of E unity Table 4 anof X f Hshan Hongping of Z Hengshiliang of X Xiaojiaw Jiugon Comm gshan o Huangjingshan ohu uan of G Manaog** p< 0.01; * p< 0.05, n

With the species number from the most common to the rarest as the abscissa, and with the observed and fitted values of species abundance as the ordinate, the curves of the three ecological niche-f itted curves of the tree, shrub and herb layers are shown in Fig.1. Only the prediction curve of the shrub layer of Enshi was close to the observation curve by ONM, with higher goodness-of-f it. BSM better fitted the herb layers of Xianfeng, Jianshi and Gucheng, and the shrub layers of Enshi, Jianshi and Gucheng. The NPM had high goodness-of-f i t for the tree, shrub, and herb layers of Jianshi,the herb layers of Xuan’en and Tongshan, and the shrub layer of Xianfeng. NPM had the higher goodness-of-f it for different layers in number, followed by BSM and ONM. The species number and arrangement of plant individuals are as follows: herb layer > tree layer > shrub layer. As a dominant species,T.ciliata was more abundant. The abundance of dominant species in the shrub and herb layers decreased successively but the evenness gradually increased.

Statistical models

In Table 5, the fit and test of the LSD shows that it accepted the tree layers of Enshi (AIC = 10.414,p of χ20.184 and p of K-S 0.938), Xuan’en (AIC = 13.324,p of χ20.184 and p of K-S 0.329) and Gucheng (AIC = 6.805,p of χ20.130 and p of K-S 0.055). The LSD also interpreted the feasible goodness-of-f i t of the shrub layers of Xuan’en (AIC = − 12.506, p of χ20.073 and p of K-S 0.329) and Zhushan (AIC = 11.962,p of χ20.123 and p of K-S 0.076). The only herb layer accorded to LSD (AIC = − 5.972,p of χ20.771 and p of K-S 0.124) was that of the Tongshan community.

The log-normal distribution (LND) model could better interpret SAD models of most tree, shrub and herb layers of the T.ciliata communities (Table 6), which is similar to the results of Preston (1948), Magurran and Henderson(2003), and Gao et al. (2011). This explains the SADs of the trees, but it was not suitable to fit those of the shrubs (p of χ2< 0.05) of Tongshan and the herb layers (p of χ2< 0.05) of Xianfeng and Gucheng. The LND had better goodness-of-f i t for the Xuan’en tree layer (AIC = − 11.393, p of χ20.647 and p of K-S 0.541), optimal goodness-of-f i t for the shrub layer of Enshi (AIC = − 2.166,p of χ20.750 and p of K-S tests 1.000) and for the herb layer of Tongshan (AIC = − 14.818,p of χ20.675 and p of K-S 0.627).

Fig. 1 (continued)

The fit and test results indicate that the Weibull distribution model (WDM) only rejected the herb layer of Xuan’en community (p of χ2= 0.000) but accepted the tree,shrub and herb layers of the other communities (Table 7).There were no significant differences between the actual observed values and the fitted values (p of χ2> 0.05), and therefore the two- parameter WDM had the most extensive fitting width for different tree, shrub and herb layers.The WDM also had the highest goodness-of-f it for the tree layer of Xuan’en (AIC = − 9.658, p of χ20.696, p of K-S test 0.938), the shrub layer of Enshi (AIC = − 3.813, p of χ20.616, p of K-S test 1.000), and the herb layers of Tongshan(AIC = − 8.659, p of χ20.587 and p of K-S test 0.964) and Zhushan (AIC = − 1.096, p of χ20.594 and p of K-S 1.000).

The curves of the WDM (Fig. 2) are the direct expressions of SAD differences in different layers. Except for the herb layer of Tongshan community, the numbers of herbs in the other communities were the highest of three vegetation layers. The species numbers of Xianfeng and Enshi were as follows: herb layer > shrub layer > tree layer; the species numbers of the shrub and the herb layers of Xuan’en were almost equal; the species numbers of Jianshi, Zhushan and Gucheng communities were:herb layer > tree layer > shrub layer. The WDM data were consistent with the observed statistics, and explained the SADs of different layers of the communities.

p 0.000**0.076 0.002**0.124 0.000**0.021*D 0.652 0.467 0.700 0.000**0.647 0.556 0.684 0.571 0.647 0.002**p 0.130 0.002**0.664 0.065 0.771 0.045*0.383 0.098 4.086 χ2 17.273 0.880 5.462 0.085 6.225 1.922 4.829 Herb layer AIC 20.226 11 34.1−9.831 18 18.1−5.972 99 12.0 7.066 59 17.6 0.031*79 1**0 0**0.62 0.32 6 1**0.00 0.00 p 0.27 0.07 0.00 0.833 D 0.600* 0.500* 0.375 0.818 0.929 0.545 0.667 0.141 p 0.009*0.073 0.096 0.001*0.123 χ2 0.733 0.025*9.344 2.778 2.169.603 3.215 140.116 4.196 rub layer Sh 5.022 AIC− 0.106.477 17−12.506−10.443−0.775−19.318.962 119.309 989 3**0485 0.93 p 0.13 0.32 0.00 0.12 0.27 0.08 0.05 nities mu D 0.286 0.600 0.800 9 4.653 0.031* 0.625 p 6 4.790 0.029* 0.667 in the eight T. ciliata com χ2 4 1.768 0.184 SD 0 0.912 0.340 Tree layer 5.41 SD 10.414 4.841 0.184 3.32 7.79 0.600 7 6.257 0.012* 0.556−1 5 2.288 0.130 0.44−5.817 6.734 0.010* 0.500 0.85 6.80 ing to L Fit and test results of L g AIC ianfen uang uan’en Qinglonghe of Jianshi ot conform iliang of X ongshanshif Hshan Table 5 nshi an unity f T Huangjingshan ohu of X ucheng Hongping of Z Hengsh Comm Maluhe of E Xiaojiaw Jiugongshan o uan of G Manaog** p< 0.01; * p< 0.05, n

p 0.627 0.964 0.270 0.938 0.627 0.336 1.000 0.964 D 0.375 0.250 0.500 0.286 0.375 0.444 0.125 0.250*p 0.000*0.191 0.638 0.395 0.675 0.219 0.102 0.048*χ2 29.5580 351357 7.42 3.40 5.17 3.16 8.27 9.17 4.50 layer 32 Herb AIC 6.25 9.59 20.070.433−2−14.884 13.077−1.99122.11 0.441 p 1.000 0.627 0.938 0.699 0.979 0.938 0.893 00563263 D 0.20 0.50 0.37 0.28 0.33 0.22 0.28 0.33 p 0.521 0.750 0.568 0.489 0.035*0.248 0.363 0.235 8500 χ2 0.57 3.87 2.25 3.43 13.5898 90 5.40 8.03 3.19 b layer Shru 0 AIC−10.58−2.1660−13.51−8.187−1.555−6.38621.55−0.379 0.938 p 0.938 0.541 0.938 0.627 0.964 1.000 0.541 munities D 0.286 0.286 0.42960.28 0.250 0.143 0.375 0.429 r diff erent T. ciliata com 0.30 0.328 5724471 p 0.64 0.11 0.22 0.09 0.24 0.20 4.805 χ2 4.651 7.485 2.487 6.955 9.418 5.416 5.979 ND fo ND.703−62.588.769−0 Tree layer−1 AIC−11.393.869.724−0−83.268.747 ing to L Fit and test results of L ianfeng uang ot conform iliang of X nshi uan’en ongshanshi of X f H f Zf T Table 6 Jiugongshan o hushan unity an Hengsh Xiaojiaw Hongping o Maluhe of E Qinglonghe of Jianshi Huangjingshan o ucheng uan of G Comm Manaog** p< 0.01; * p< 0.05, n

p 0.964 0.964 0.627 0.938 0.964 0.699 1.000 0.964 D 0.250 0.250 0.375 0.286 0.250 0.333 0.125 0.250 36 0**87749 p 0.10 0.32 0.00 0.46 0.58 0.44 0.59 0.60 4.647 9.147 2.543 3.741 4.750 3.698 2.700 Herb layer χ2 118.234 AIC 40 17.5 9.164 87 17.6 6.767−8.659 9.211−1.096 4.900 p 30489980 0.98 1.00 0.96 0.93 0.97 0.69 0.93 1.00 0.333 D 0.200 0.250 0.286 0.222 0.333 0.286 0.167 p 0.266 0.161 0.440 0.616 0.079 0.181 0.163 0.273 χ2 6.555 2.649 0.252 2.700 08 7.575 5.122 2.598 rub layer 11.3 Sh AIC−5.103−3.813−10.564−2.259 1.495−1.048 6.175−2.742 p 0.938 0.938 1.000 0.938 0.627 1.000 1.000 0.591 munities D 0.286 0.143 0.286 0.286 0.375 0.125 0.143 0.417 in the eight T. ciliata com p 0.160 0.161 0.696 0.145 0.407 0.113 0.217 5.171 0.313 5.147 χ2 1.443 5.395 5.077 7.480 3.560 4.450 DM DM 3.592 3.323 ing to W Fit and test results of W Tree layer AIC−1.512−2.212−9.658−0.216−3.770−1.869 g ianfen uang uan’en Qinglonghe of Jianshi ot conform f Tf Hshan iliang of X ongshanshi nshi Maluhe of E unity of X Jiugongshan o Table 7 an ucheng Hongping of Z Hengsh Comm Xiaojiaw Huangjingshan ohu uan of G Manaog** p< 0.01; * p< 0.05, n

Discussion

T. ciliatais a strong light-demanding species, so light is a main restriction factor. Under natural growing conditions,it colonizes adrets or southern slopes alongside streams,valleys and forest edges for maximum sunlight to maintain its carbon balance (Zheng et al.2019). In the communities in this study, as a pioneer species,T. ciliatadominated the canopies.

In some instances, specifi c site conditions, however, made the light environment in the middle layers suitable, so the species richness of the herb layers was higher, while the regeneration of T.ciliata saplings and shrubs was limited.If no anthropogenic disturbance occurs, the communities would progress to climax communities, in which different plant layers could make full use of environmental resources.Due to the various ecological conditions in the different T.ciliata communities, interpretations of the different fitting models and the goodness-of-f it differ in different ways.Only when the mixed application of different SAD models is adopted, can the optimum SAD model(s) be determined for the monitoring and management of the restoration of these communities (Zhang 1999; Peng et al.2003; Reng et al.2009; Cheng et al.2011; Gao et al.2011; Zhang et al.2015; Fang et al.2016; Zhong et al.2018).

Comparison of ecological niche models

The niche theory suggests that there may be more than one process at work during forest recovery, acting differently on common and rare tree species (Kraft et al.2015; Meiners et al.2015).

The broken stick model (BSM) is suitable for communities lacking species of relative importance and species richness is not high but relatively evenly-distributed (Gao et al.2011). The BSM has higher goodness-of-f it only in communities with nearly equal species abundances (May 1975),which helps to explain why most tree layers could not accept BSM. BecauseT. ciliatais an important species in the communities, once occupying the canopy it would weaken the competitiveness of other tree species and make the richness of shrub layers low so that shrubs had comparatively even distribution. The consequence was that most shrub layers in the eight T.ciliata communities were acceptable to the BSM. With herb species abundance high, only three herb layers with the highest evenness in Xianfeng (E= 0.846),Jianshi (E= 0.855) and Gucheng (E= 0.861) were acceptable to BSM, the result of which was consistent with Gao et al. (2011).

Ecological niches of different species in a community may inevitably overlap to varying degrees because of species sharing resources over the long-term, which will embody complex interspecies relationships, both in spatial distribution and in quantity (Xu et al. 2018). Zhang (1999)fitted the species abundance distribution for deciduous broad-leaved forests in New York State with the overlapping niche model (ONM) and found that ONM was suitable for both simple and complex communities. Species in a community fitted with ONM are not strongly dependent on each other, but the ecological niches of each may overlap and differences in the use of resources are not significant (Feng et al. 2007). Since the evenness E of the shrub layers in Enshi, Jianshi and Gucheng communities were 0.930, 0.871 and 0.916, and of the herb layer in Jianshi 0.871, each being the highest within the communities, ONM was optimally suitable for these layers (Table 3; Fig. 1).

Fig. 2 Fitted curves of different layers of T. ciliata communities with WDM

The niche preemption model (NPM) is only suitable for a community of few species or in the early stages of community succession (Hubbell 2001), where a few common species account for the majority of individuals and there are several rare species, each with a few individuals (Spitale 2012; Campos et al. 2018; Villa et al. 2018a). As the dominant species of the tree layers, the average species ratio ofT. ciliataaccounted for 45.6% of all tree species,colonizing the canopy and dominating resources. In the competitive environment jointly constructed with the herb layers of relatively high abundance, demands of shrub species in the ecological niche can not be fully satisfied and do not develop in number (Ma et al. 1997; Wu et al.2001). NPM, therefore, is suitable for the explanation of SADs of shrub layers (see Table 4; Fig. 1).

The broken stick model (BSM) fitted the SADs of one tree layer, five shrub layers and three herb layers;the overlapping niche model (ONM) was only suitable for three shrub layers and one herb layer; and the niche preemption model (NPM) was applicable for two tree layers, three shrub layers and three herb layers. The fit breadth and goodness with different models was of the order: BSM > NPM > ONM.

Comparison of statistical SAD models

The fit breadth and goodness of the three statistical models arranged from the best to the worst as follows:WDM > LND > LSD. The parameter α of the log-series distribution (LSD) model, as a species diversity index,could effectively characterize diversity differences of a community (Motonura 1932). α was not sensitive to the change in abundance of rare or of common species but highly sensitive to the change of species in moderate numbers (Kempton and Taylor 1974a, b; Ma 1994).When Shannon-Weiner H, evenness E, richness S of the eight communities were compared with the parameters of LSD, no evident correlations between the parameters and concentrated or rare species were found. This might be related to the LSD model or the sampling and requires further research. Although many Chinese researchers have achieved preferable results with the LSD model for SADs (Jiang et al. 1995; Xie and Chen 1997; Ma et al.1997; Gao et al. 2011), the model had no ideal goodnessof-fit for the various layers in theT. ciliatacommunities.

The log-normal distribution (LND) model itself is the result of a random process. The communities that fit the model, have greater species diversity and more ecological niches, allowing for more uniformly distributed plant communities (Magurran 2004; Fattorini et al. 2016). If a community has a higher species richness and more even distribution, its SAD can better conform to the LND (Yin and Liao 1999). The average evenness E of the tree, shrub and herb layers of the communities were 0.789, 0.704 and 0.674, indicating the distributions were relatively even.LND thus had favourable fit breadth and goodness for SAD models of the communities.

The scale parameter b, shape parameter c of the Weibull distribution model (WDM) and Shannon-Weiner index H and evenness E were significantly correlated,suggesting that the model not only had the highest goodness-of-fit for various layers, but also could interpret the ecological meanings in the composition and function of the eight communities in explaining SAD models.

Interpretation of α diversity with SAD models

The parameters of LSD, LND and WDM of all layers are shown in Table 8. The parameter α of LSD represents species diversity (Magurran and Henderson 2003), reflects the characteristics of various layers and shows diversity differences among communities. When α was lower, dominant species were more abundant than rare ones (Table 8). S 0 represented the largest species number in the modal octave and λ revealed that the shrub layers had the most concentrated distribution patterns of all layers. The parameter b of WDM does not fully reflect the size of the octave grouping because b may be restricted by the sampled areas (Qin et al.2009). The shape parameter c can reflect the traits of species diversity and is an indicator with certain ecological meanings (Wu et al. 2004).

Correlation analyses were made of the parameters of the three statistical models, species richness S, Shannon-Weiner index H and Pielou evenness E (Table 9). The parameter α, b and λ of the log-series distribution (LSD) model were significantly correlated with S, H and E, indicating that α more effectively reflected community diversities (Magurran 1988; McGill 2010) and proving that there existed consistency between the concentration tendency of SADs and α diversities. The research result agreed with Wu et al. (2004).

Conclusions

This research indicates that species abundance distribution models may explain significances of ecological differences and better reflect a community’s traits than commonly-used diversity research methods (Guo et al. 2007). The adoption of these models is proposed as a complementary method to evaluate community recovery (Villa et al. 2019). The goodness-of-f it of the statistical models were superior to those of the niche models. In addition, the statistical models can optimally interpret the biodiversities of theT. ciliatacommunities. By comparison, the parameters of the Weibull distribution model, with an extensive fitting range and highest goodness-of-f it, can explain the ecological meanings of the Shannon-Weiner index H and evenness E and interpret the structure and assembly of the eightT. ciliatacommunities. Therefore, the Weibull distribution model is practicable and maneuverable. By comparing the species abundance distribution models with the relevant Weibull distribution model curves, comprehensive and detailed traits of species diversities of various layers within the same community or of different communities can be achieved (Qin et al. 2009).This is consistent with other research results (Wu and Hong 1997; Wu et al. 2004).

Table 8 Parameters of LSD,LND and WDM in the eight T.ciliata communities

Table 9 Correlation Analysis of species diversity indexes and parameters of statistical models

According to the traits of the population structures and distribution patterns ofT. ciliata(Wang et al. 2016a, b),anthropogenic disturbances changing species coexistence conditions are preferred, according to the existing niches with environmental requirements (water, nutrients, light availability) at the habitat scale. For example, in the less uniformT. ciliatacommunities, selective removal of pioneerT. ciliatashould be planned in order to increase the number of individuals of other species to enhance diversity (Wang et al. 2016a, b; Villa et al. 2019). Under low or moderate disturbance, and with nearby seed sources, tree species richness increases rapidly during forest succession (Guariguata and Ostertag 2001; Zermeño-Hernández et al. 2015). Communities with high biodiversity and higher species ranking in species abundance distribution patterns are ideal for the conservation of endangered species (Reng et al. 2009). And higher species ranking in SAD patterns can drive multiple changes in forest functioning (Tabarelli et al. 2010; Ali et al.2019). The species abundance distribution models, with the Weibull distribution model as optimum for the eightT. ciliatacommunities, can perform monitoring functions for promoting α diversities and changes in species distribution for conservation and forest management.

Due to the wide distribution ofT. ciliatain Hubei Province, the complex and changeable community environments,and the large differences in species and in individual numbers among different layers within the communities, it is difficult for any single ecological niche or statistical model to fully clarify the ecological significances of different layers in different communities. Theoretical species abundance distribution models and diversity indices should be adjusted according to the restoration needs of each environment (Fattorini et al. 2016; Villa et al. 2019), and the intensification of management, (selective thinning for example), should also be monitored to avoid a reduction in diversity (Villa et al.2018b). The mixed application of various models and effective tests, together with management in the long-term, could reveal community structure, quantitative characteristics and resource status, and provide a basis for the conservation of biodiversity of theT. ciliatacommunities.

AcknowledgementsWe sincerely thank Prof. Zhongcheng Zhou, Mr.Yinshan Tan (Badong County Forestry Bureau) and numerous foresters from different forestry bureaus of Hubei Province for their support of our site surveys. We also express our sincere gratitude to the reviewers for their constructive criticisms.