Comparative performances of new and existing indices of crown asymmetry: an evaluation using tall trees of Eucalyptus pilularis(Smith)

Fanlin Kong · Huiquan Bi · Michael McLean ·Fengri Li

Abstract Over the past 50 years, crown asymmetry of forest trees has been evaluated through several indices constructed from the perspective of projected crown shape or displacement but often on an ad hoc basis to address specific objectives related to tree growth and competition, stand dynamics, stem form, crown structure and treefall risks.Although sharing some similarities, these indices are largely incoherent and non-comparable as they differ not only in the scale but also in the direction of their values in indicating the degree of crown asymmetry. As the first attempt at devising normative measures of crown asymmetry, we adopted a relative scale between 0 for perfect symmetry and 1 for extreme asymmetry. Five existing crown asymmetry indices (CAIs) were brought onto this relative scale after necessary modifications. Eight new CAIs were adapted from measures of circularity for digital images in computer graphics, indices of income inequality in economics, and a bilateral symmetry indicator in plant leaf morphology. The performances of the 13 CAIs were compared over different numbers of measured crown radii for 30 projected crowns of mature Eucalyptus pilularis trees through benchmarking statistics and rank order correlation analysis. For each CAI, the index value based on the full measurement of 36 evenly spaced radii of a projected crown was taken as the true value in the benchmarking process. The index (CAI 13 )adapted from the simple bilateral symmetry measure proved to be the least biased and most precise. Its performance was closely followed by that of three other CAIs. The minimum number of crown radii that is needed to provide at least an indicative measure of crown asymmetry is four. For more accurate and consistent measures, at least 6 or 8 crown radii are needed. The range of variability in crown morphology of the trees under investigation also needs to be taken into consideration. Although the CAIs are from projected crown radii, they can be readily extended to individual tree crown metrics that are now commonly extracted from LiDAR and other remotely sensed data. Adding a normative measure of crown asymmetry to individual tree crown metrics will facilitate the process of big data analytics and artificial intelligence in forestry wherever crown morphology is among the factors to be considered for decision making in forest management.

Keywords Projected crown shape · Circularity ·Inequality · Bilateral symmetry · Rank order · Eucalyptus pilularis

Introduction

Trees grown in an open and unrestricted space free from competition, prevailing winds or directional solar radiation,as where it occurs at high latitudes, tend to develop round and symmetrical crowns with a near circular vertical crown projection area (Krajicek et al. 1961; Wade and Hewson 1979; McPherson and Rowntree 1988; Aakala et al. 2016).In a competitive environment dominated overwhelmingly by asymmetric competition for light in either natural or planted forests, trees often form asymmetric or irregular crowns with highly variable radius along different radial directions as conventionally measured from the stem base to the projected crown edge at breast height or ground level (Curtin 1970;Fleck et al. 2011; Xu et al. 2013; Pretzsch 2014; West and Smith 2019). Consequently, the shape of crown projection area centred around the stem base departs from circularity,while the crown centre, often represented by the centroid of the crown projection area, also moves away from the base of the tree (Umeki 1995a, b; Rouvinen and Kuuluvainen 1997;Uria-Diez and Pommerening 2017). The asymmetric crown projection area that have been traditionally assessed on the ground by looking up through a conventional hand-held crownometer reflects the top-down view of the asymmetric crown that can now be digitally constructed in 3-dimensional space using LiDAR scanned, segmented or delineated point cloud data and individual tree crown delineation algorithms (Seidel et al. 2011; Metz et al. 2013; Xu et al.2013; Trochta et al. 2017; Hess et al. 2018; Krůček et al.2019; Hastings et al. 2020).

The formation of asymmetric crowns in a crowded forest stand has been considered primarily as a result of crown plasticity, i.e. competition-induced adaptive morphological shifts in response to the constantly changing light conditions of individual trees as they grow and compete for the unidirectional resource within the stand (Grams and Andersen 2007; Purves et al. 2007; Longuetaud et al. 2013). Thus,crown asymmetry is largely driven by the adaptive strategy of individual trees to maximize light exposure by rearranging some elements of the crown architecture away from light limiting canopy space due to crown overlap or physical obstructions from immediate neighbours through directional lateral crown expansion and/or contraction by self-pruning of branches and shedding-offof crown parts (Curtin 1970;Franco 1986; Grams and Andersen 2007; Pretzsch 2014;Uria-Diez and Pommerening 2017). The competitioninduced crown asymmetry can also be augmented to some extent by the mechanical abrasion, breaking and droppingoffof branches and crown parts due to crown collisions,wind, snow and fire damage or other environmental factors that are independent of competition for light (Wooldridge et al. 1996; Dunham and Cameron 2000; Brüchert and Gardiner 2006; Meng et al. 2006; Teste and Lieffers 2011; Bar-Ness et al. 2012; Hajek et al. 2015). Such asymmetric crown expansion enables the competing trees to quickly fill emerging gaps in a crowded stand and to occupy canopy space released by silvicultural thinning in plantations (Siemon et al. 1976; Longuetaud et al. 2013; Han et al. 2014; Pretzsch 2014). The dynamic mosaic assemblage of asymmetric plastic crowns of individual trees at a local neighbourhood scale would collectively lead to a reduction in crown overlap in the canopy, fuller and better optimised canopy space occupation,and improved growth performance at a stand level (Vincent and Harja 2008; Jucker et al. 2015; Uria-Diez and Pommerening 2017; Engel et al. 2018; Krůček et al. 2019). In this process of dynamic puzzle-like assemblage, crown asymmetry was regarded not only as a passive adaptive response to neighbourhood competition but also as an active driver of canopy and stand dynamics at the same time (Umeki 1997;Vincent and Harja 2008; Engel et al. 2018).

Because crown asymmetry plays a central role for trees within a crowded stand in acquiring competitive advantages through improved light interception, in avoiding themselves being overtopped by taller neighbours, in optimising canopy space occupation, and in their growth, canopy and stand dynamics, it has been increasingly assessed and quantified in forest and ecological research over the past 50 years (Curtin 1970; Franco 1986; Young and Hubbell 1991; Umeki 1995a;Brisson 2001; Krůček et al. 2019). A number of crown asymmetry indices (CAIs) have been proposed to indicate the degree of crown asymmetry but from different perspectives, which can be put into three broad categories based on their focus and derivation. The first category focuses on the shape of the crown projection area that is usually represented by the polygon constructed from a varying number of radial measurements, which includes the indices proposed by Curtin (1970), Young and Hubbell (1991), Young and Perkocha (1994) and Lei et al. (2012). Also belonging to this category is the assessment and classification of crown asymmetry through image analysis of vertical photographs of tree crowns reported in a case study by Brown et al.(2000), albeit not through a continuous index. The second category uses the vector between the tree base position and the crown centre to measure the magnitude and direction of crown asymmetry. In determining the crown vector, the crown centre has usually been represented by the centroid of the crown projection area (Kio 1970; Franco 1986; Young and Perkocha 1994; Umeki 1995a, b; Uria-Diez and Pommerening 2017), and only seldom by an estimated crown mass centre (Rouvinen and Kuuluvainen 1997; Seidel et al.2011). As a further step from the crown vector, which shows crown displacement in a projected 2-dimensional plane, the third and most recent category computes the percentage crown volume in a particular crown sector or the relative displacement of tree crown volume from its assumed symmetric shape and position in a 3-dimensional space using terrestrial laser scanning (TLS) data (Olivier et al. 2016;Krůček et al. 2019).

These indices were constructed for specific research objectives and practical applications such as relating tree and crown structures (Curtin 1970; Kio 1970), assessing the risk of trees falling into gaps (Young and Hubbell 1991;Young and Perkocha 1994), examining neighbourhood competition (Rouvinen and Kuuluvainen 1997; Seidel et al.2011; Aakala et al. 2016; Uria-Diez and Pommerening 2017;Vovides et al. 2018; Krůček et al. 2019), modelling individual tree growth (Umeki 1997; Engel et al. 2018), depicting stand dynamics (Umeki 1997; Pretzsch 2014), and discerning the influence of topography and other environmental factors on crown structure (Umeki 1995a, b; Aakala et al.2016; Vovides et al. 2018). As these objectives and practical applications were interrelated, the indices shared some similarities, but differences among them remain not only in the scale but also in the direction of their values in indicating the degree of crown asymmetry. An index like the crown vector may give values that indicate different degrees of crown asymmetry for identically shaped trees of different sizes as noted by Seidel et al. (2011). These differences render the indices noncomparable even for the same set of crown measurements from individual trees, let alone for results from different studies. The comparative performances of these indices over different numbers of measured crown radii have not been evaluated. Among data from field measurements of past and on-going experiments, research and inventory plots, the number of conventionally measured radii for an individual tree has mostly varied from 2 to 8 as indicated by our survey of more than 50 papers published over the last 50 years. In a rare case, even 16-sided polygon was used to represent crown projection areas (Sillett and Goslin 1999).The choice of which index or indices to use or not to use for each case requires a good understanding of the comparative performances of these candidate indices.

Fundamentally, the differences among the CAIs reflect different perceptions of crown asymmetry, a widely used but not commonly and clearly def ined term in the forestry and ecological literature. For a crown projection area that is centred around the tree base and represented by the polygon constructed from a numbers of crown radius measurements,the degree of departure from circularity in its shape serves as a natural indicator of the degree of crown asymmetry.From this perspective, the aims to: (1) evaluate the existing CAIs following a comprehensive review of the literature over the past 50 years, and after necessary modifications,to place them into a unified framework on a relative scale between 0 and 1, with 0 indicating perfect symmetry and 1 extreme asymmetry, in order to improve their comparability;(2) introduce new indices of crown asymmetry on the same relative scale; (3) evaluate the comparative performances of the new and existing indices over different numbers of measured crown radii for individual trees using detailed crown radius measurements from tall trees of Eucalyptus pilularis in a correlated curve trend (CCT) experiment; (4) identify the best performing CAIs for research and management applications. The latest volumetric indices of crown asymmetry from TLS data are not included in the evaluation as they are beyond the research scope.

Materials and methods

Existing CAIs and their modifi cations

As the first category of crown asymmetry indices focuses on the shape of the projected crown polygon constructed from a varying number of radial measurements, the variability or inequality of crown radii has been used to indicate the degree of crown asymmetry. Three existing indices fall into this category. The first was proposed by Curtin (1970), who used the ratio of the longest radius over the mean radius of all six equally spaced radii. Although the values of this index are on a unitless scale, they are greater than 1 for any asymmetric crowns, but the maximum value is not def ined.To bring the values onto a relative scale between 0 and 1,this index was modified as follows:

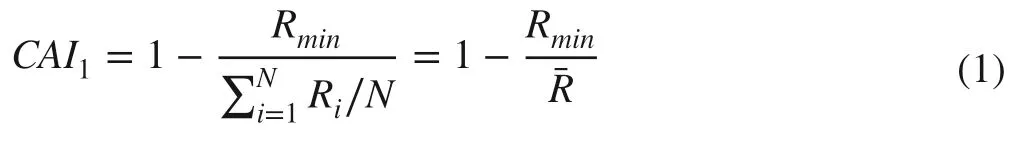
where CAI1is the acronym of crown asymmetry index with a given sequential number 1 in the subscript, R i represents the length of theith radius in m, N is the total number of crown radii, and R min is the shortest crown radius among the N radii (Fig. 1). The second was proposed by Young and Hubbell (1991) when examining tree-falls in relation to crown asymmetry in a moist tropical forest. A line was drawn across the projected crown polygon through the tree base in the direction that maximized the area on one side of the crown. The index was then def ined as the proportion of total crown area accounted for by this larger area and so it varied between 0.5 for symmetric crowns and 1.0 for what they termed as complete asymmetric crowns. This index was brought onto a relative scale between 0 and 1 through the following transformation:

The second category of existing crown asymmetry indices uses a crown vector as a measure of crown eccentricity to show the size and direction of either absolute or relative crown displacement. Kio (1970) appeared to be the first in the literature to use an absolute crown vector calculated for an 8-sided polygon formed by joining the extremities of the measured crown radii when examining the crown asymmetry and radial distribution of buttress flanges of tropical forest trees. Such use of absolute crown vectors have been adopted in a number of studies for specific research objectives (Young and Perkocha 1994; Umeki 1995a, b, 1997;Seidel et al. 2011; Uria-Diez and Pommerening 2017). However, as noted by Seidel et al. (2011), the absolute crown vector tends to increase with tree size, indicating different degrees of crown asymmetry even for identically shaped trees of different sizes.

Franco (1986) subsequently proposed a standardized vector within a unit reference circle as a more general approach to the analysis of growth and form of competing modular organisms. This standardized vector can be readily adopted as a measure of crown asymmetry as shown below:

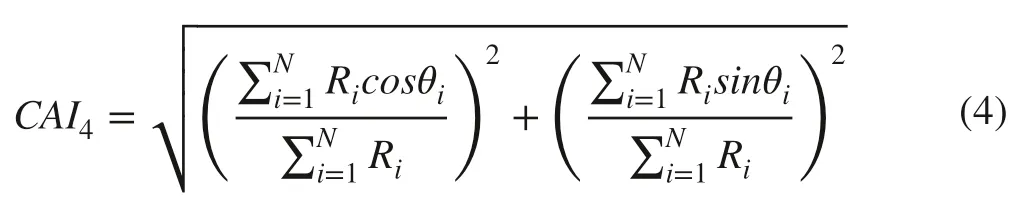
where θiis the angular orientation of Riwith respect to a reference point, such as north (Fig. 1). This index equals zero for symmetric crowns with a perfectly uniform circular distribution of Riand approaches 1 for extremely asymmetric crowns. In addition, the direction of asymmetry is indicated by the direction of the standardized vector.

Another relative measure of crown asymmetry was the ratio of the length of the crown vector over the square root of crown projection area. This measure was used only by Young and Perkocha (1994) for evaluating the crown displacement of tropical forest trees and its value varied between 0.02 and 3.47. As this measure is not mathematically bounded by 1,it was modified as follows:

where square brackets are used to denote the distance from the stem base (Sb) to the crown centre (Cc), represented by the centroid of the projected crown polygon, as opposed to their products, and Rmaxis the longest crown radius among all measured crown radii (Fig. 1). Like CAI2, this index is based on the projected crown area and so its calculation also requires a minimum of three radius measurements.

A very similar index to CAI4was used by Brisson (2001)for examining the neighbourhood competition and crown symmetry of sugar maple trees, where their projected crown areas were represented by 8-sided convex polygons (i.e. the internal angles are all less than 180°). This particular index was adopted from Mead’s (1966) measure of abcentricity of convex Thiessen polygons in spacing and yield experiments with carrots. It is calculated as the length of the crown vector divided by the weighted mean distance of the centroid of the projected crown polygon from the vertices, where the weight for each vertex is obtained by dividing the difference between π and the interior angle of the polygon at the vertex with the sum of such differences for all vertices.Like CAI4, this index also takes values between 0 and 1,but cannot be readily applied to nonconvex projected crown polygons. If the weighted mean distance in its calculation is replaced simply by the mean crown radius,in a necessary modification for more general application, the modified index would be equivalent to CAI4. Therefore, it was not evaluated in this study. Another ad hoc measure of crown displacement tried in Young and Perkocha (1994) was the degree of deflection def ined as the angle between vertical and the line between the stem base and the centre of crown area at a level equal to total tree height. Although useful for the evaluation of treefalls in their study, this measure does not lend itself for more general applications and so was also not evaluated here.

New crown asymmetry indices

There is a wealth ofliterature in the fields of computer graphics, image analysis, pattern recognition, economics and plant leaf morphology where measures of circularity,inequality and symmetry have been established for various purposes (Haralick 1974; Sen 1997; Di Ruberto and Dempster 2000; Montero and Bribiesca 2009; Herrera-Navarro et al. 2013; Stojmenovic et al. 2013; Xiao and Wang 2013;Shi et al. 2018). Although not all applicable to our specific case of measuring crown asymmetry using only a small number of evenly and angularly spaced crown radius measurements, the ideas and principles behind some of these measures led us to propose and adapt eight new measures of crown asymmetry.

New CAIs based on the measures of circularity for digital images

In calculating the first new measure, each of the measured crown radii of a tree was divided by their maximum and converted to relative crown radius ri=Ri∕Rmaxon the unit scale (0, 1). The standard deviation of the relative crown radius r was multiplied by 2 as our proposed new measure of crown asymmetry:

where N is the total number of measured crown radii as in Eq. 1. The multiplier of 2 was based on the fact that the maximum variance of a random variable following the beta distribution is 0.25 (Gupta and Nadarajah 2004), which was a reasonable distributional assumption for r . The second new measure was adapted from one of the measures of circularity for digital figures proposed by Di Ruberto and Dempster(2000) based on mathematical morphology:

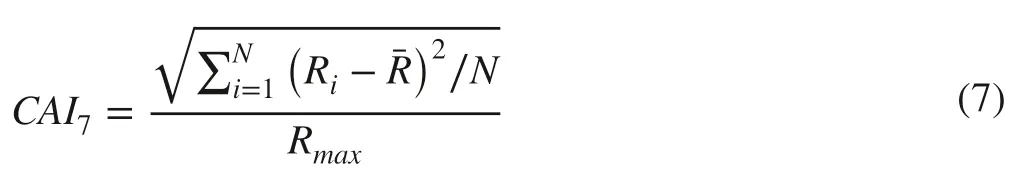
The third new measure was essentially the same as the mean roundness measure described in Herrera-Navarro et al.(2013) for digital image characterisation, but only rescaled for it to take values between 0 and 1:

The mean roundness measure was well tested by Herrera-Navarro et al. (2013) using 100 computer-generated regular polygons with the number of sides ranging from 3 to 100 and also though real magnified images of fine graphite particle of varies shapes.

New CAIs based on economic inequality metrics

The Gini coefficient, first introduced by Corrado Gini in a 1912 book published in Italian (Ceriani and Verme 2012 for English extracts) and now the most widely used index of economic inequality (Allison 1978; Sen 1997; Xu 2004;Heshmati 2004; Langel and Tillé 2013; Bowles and Carlin 2020), was taken as the fourth new measure of crown asymmetry. Although there have been many formulations and interpretations of the index (Xu 2004; Langel and Tillé 2013), its calculation is predominantly based on the Gini’s mean difference, i.e. the average absolute difference between all pairs of observations:

Its geometric interpretation is based on the well-known Lorenz curve in economics (Lorenz 1905). For a population whose individuals are ordered by income level from the lowest to the highest, the curve plots in a unit square the cumulative proportion of total income of the population against the cumulative proportion of individuals. The Gini index is the ratio of the area between the 45-degree line of unity for perfect equality and the Lorenz curve to the area beneath the line of unity.

The Gini index has been adapted to indicate size inequality in plant populations (Weiner and Solbrig 1984;Weiner 1985), competition status and growth dominance of trees in forests (Bi 1989; Binkley et al. 2006; West 2014), and tree size diversity in forest management (Lexerød and Eid 2006). Its theoretical range is from 0 to 1, i.e.from compete equality to extreme inequality. However, its maximum value for a finite sample of N observations is equal to (N − 1)∕N (Bendel et al. 1989; Deltas 2003). As the upper bound of Gini increases with sample size, e.g.from 0.50 to 0.94 when N varies from 2 to 16, the range of Gini increases substantially with N for small sample size as in our case. For any value of N in small samples to have the same range of (0, 1), the linearly adjusted Gini of Deltas (2003), as also alluded to in Jasso (1979), was adapted here as an alternative measure of crown asymmetry:

As the adjusted Gini, CAI9also ranges from 0 for perfect symmetry to 1 for extremely asymmetric crowns, but it corrects the downward bias of Gini for small samples.

Another commonly used inequality index similar to but much simpler than the Gini index is the Hoover index,which was originally introduced to measure the industrial localization and the evenness of the geographical distribution of population in the U.S. by Hoover (1936, 1941).It shared the same formulation as the lesser known Pietra-Ricci inequality index that was published in Italian some 20 years earlier (Frosini 2012). The Hoover index is functionally related to the Gini index and graphically represents the maximum vertical distance between the Lorenz curve and the 45-degree line of perfect equality (White 1986; Long and Nucci 1997; Rogerson 2013). It was also adapted in this study as the fifth new measure of crown asymmetry as follows:

Although the most widely used summary statistic of economic inequality, the Gini coefficient is not without limitations. A major one is that it is not easily decomposed into additive components reflecting the contribution of inequality within and inequality between subgroups (Atkinson 1970;Xu 2004). The same Gini coefficient can represent Lorenz curves for very different income distributions. As such,it does not capture social welfare or policy interventions that bridge inequality between rich and poor. To overcome this weakness beyond the conventional summary measure of inequality, Atkinson (1970) introduced a decomposable welfare-based index of inequality by examining how the Lorenz curves corresponded to different distributions from the perspective of averting inequality through a social welfare function. The literature on the principle and applications of the Atkinson index over the past 50 years is extensive;even a brief review is beyond the scope of this paper. For the sake of parsimony, a special case of the Atkinson was adopted here as the sixth new measure of crown asymmetry without providing further details:

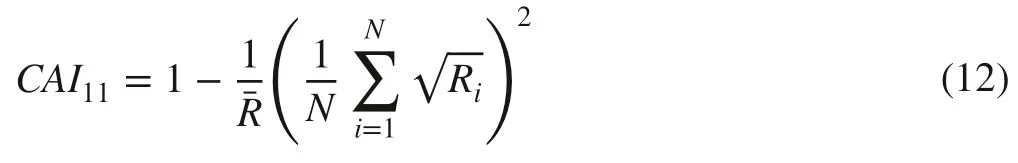
Out of a rather different motivation from the above three inequality indices based on the Lorenz curve, Theil (1967)adopted the entropy approach and derived a decomposable measure of inequality based on the information theory. Like the Atkinson index, subsequent developments and applications of the Theil index over the past 50 years also built up a substantial body ofliterature that is beyond the scope of this paper to have even a short review. The Theil index varies between zero (perfect equality) and lnN, the logarithm of total size of population to base e and so can be normalized to vary between 0 and 1 (Frosini 2012). The normalized Theil index was adopted here as the seventh new measure of crown asymmetry as shown below:

New CAI adapted from a symmetry measure of plant leaf morphology

Shi et al. (2018) proposed a simple measure for the bilateral symmetry ofleaves by dividing a leaf blade into two sides along its midrib from the base to apex and measuring the width of each side along a number of evenly spaced lines vertical to the midrib. The pairwise absolute differences in width between the two sides relative to the blade width, i.e.sum of the two paired sides, were averaged across all pairs to obtain a measure of bilateral symmetry. This measure was adapted here as the eighth new index of crown asymmetry:

where Npis the number of paired crown radius measurements,andrepresent theith pair of radii measured on two opposite sides of the crown.

Data used for evaluating crown asymmetry indices

The tree species

Occasionally attaining 70 m in height and exceeding 3 m in diameter at breast height (DBH), E. pilularis is a tall tree species with a straight trunk up to 1/2 to 2/3 of the total tree height below a densely foliaged crown (Boland et al.2006). It occurs in forests over much of the coastal area of eastern Australia from as far north as Allom lake on the Fraser Island (25.2° S) in south-eastern Queensland to its southern limit of Nadgee State Forest (37.5° S) at the far south coast of New South Wales (NSW), covering a coastline distance of more than 1800 km. The climate for most of the distribution is warm humid, with the mean maximum temperature for the hottest month in the range 24-32 °C,the mean minimum of the coldest month around 5-10 °C and mean annual rainfall about 900-1750 mm (Boland et al.2006). It can form pure stands or grow in mixtures often as a dominant species with a wide range of other associated eucalypt species. The pure and mixed stands can occur both as dry and as wet sclerophyll forests which occupy a large and def inable section of the vegetational, environmental and soil fertility gradient (Florence 1969, 1996). Because of its growth characteristics, timber productivity and quality, it has become the most extensively cultivated hardwood plantation species in NSW since the first plantations were established in the state in 1939 (Stanton 1992; Henson and Smith 2007).As an intolerant species to competition for light, E. pilularis sheds branches well on a range of sites and over a range of stand densities, including relatively isolated trees in gaps in the forest (Florence 1996; Kinny et al. 2012). Comparing to some other intolerant Eucalyptus species, it does not maintain strong apical growth and a conical crown in the same way and tends to have stronger lateral crown development occurring at an earlier stage, resulting in a more subconical type of crowns (Florence 1996).

The correlated curve trend (CCT) experiment

The data for this work came from a long-term E. pilularis correlated curve trend (CCT) experiment in Bulls Ground State Forest (152° 41′ 19″ E, 31° 33′ 42″ S), near Kew, on the mid north coast of NSW, Australia. The experiment covered a rectangular area of 3.30 ha across a gentle 7° northeast facing slope on an ex-pasture site. The mean annual precipitation is above 1200 mm, falling throughout the year but with a summer maximum in February (Cassidy et al.2012). Seedlings were planted in mid January 1964 on a grid of 2.44 m by 2.74 m (i.e. 8′ by 9′ in imperial units) that was laid out over the entire experimental area to establish an even-aged plantation with an initial stocking of 1495 ind.ha −1 . The entire planted area was divided into 3 replicate blocks and each block was subdivided into 6 equal sized squares of 42.67 m × 42.98 m in size for laying out a total of 18 experimental plots. Each plot was about 0.08 ha in size,initially containing 120 trees and surrounded by a buffer of two planting rows. Based the CCT concept of O’Connor(1935), six thinning treatments alphabetically coded from A to F were progressively applied in a randomized block design so that the growth trend in mean tree size over the full range of growing space from the smallest, represented by the unthinned control treatment (A), to the largest, represented by the most frequently and intensely thinned treatment (F)that provided free-growing space to individual trees throughout the experiment, could be concisely examined through a set of correlated curves. The origin of the CCT concept and its experimental implementations in South Africa were critically reviewed by Bredenkamp (1984). Although conceived by an inspection forester and not explored in a formal mathematical way, the CCT concept is closely related to the theory and practical applications of the C-D (Competition-Density) rule proposed and formalized by Kira et al. (1953)and Shinozaki and Kira (1961).

The times and intensities of the 6 treatments were described in detail by two previous studies (Fox et al.2007 and Cassidy et al. 2012). The control treatment (A)was never thinned. Five other treatments from B to F were thinned from below progressively between 1 and 5 times to their specified stocking levels of 988, 741, 371, 247 and 124 ind. ha −1 between the ages of 3 and 7 years. At the age of 22 years, these five treatments were thinned to the final stocking levels of 700, 450, 250, 125 and 87 trees/ha. The third replicate block was destructively sampled in 2000 to examine the sawing characteristics and wood properties of the then 36-year-old trees and the changes in the calculated log size and value across the thinning treatments from age 5 to 36 years (Muneri et al. 2003, Cassidy et al. 2012). Replicates 1 and 2 were kept to allow the experiment continue until the final harvest in early 2016 when the trees reached their early stage of maturity.

Field measurements

Before the final harvest, DBH (diameter overbark at breast height of 1.3 m) and total tree height of all individual trees in each of the 12 remaining plots were measured. A total of 30 trees were selected for detailed crown radius measurements,including 3 trees from each of the 6 plots in replicate 1 and 2 trees from each of the 6 plots in replicate 2. These trees were selected through stratified random sampling. To do so,all trees in each plot of replicate 1 were ranked by their DBH so to create three size classes: the smallest one-third, the middle one-third and the largest one-third, each containing about the same number of trees. Then a sample tree was randomly taken from each size class. If the crown of a selected sample tree could not be measured due to visual obstruction,a broken top or upper stem, another tree of similar size in the same plot was taken as a replacement. For each plot in replicate 2, only two size classes were used following tree size ranking only to reduce the exposure of the Australian authors to extreme summer heat in the field.

The vertically projected crown radius of each sample tree was measured along 36 evenly spaced radial directions from the stem at breast height using a measuring tape, a timber dowel with a clearly marked breast height, and a Geographic Resources Solutions (GRS) Densitometer™. The densitometer has been commonly used in measuring crown radius and assessing forest canopy cover (Stumpf 1993; Paletto and Tosi 2009; Iiames et al. 2018; Vovides et al. 2018). It is basically a plastic tube moulded into a “L” shape enclosing a mirror to project a view of the crown along an exact vertical line-of-sight above the measurer holding it. The vertical line-of-sight is determined by two bubble-line levels mounted inside the viewing tube. The position of crown edge along a radial direction is located when the edge is viewed through centred crosshairs drawn on the viewing lens after the measurer moves progressively away from the stem.For ease of use in the field, the densitometer was rested on top of the wooden dowel that was cut to a specific length for the measurer to see through at an ideal height. The distance from the tree trunk at breast height to the breast height of the dowel was then measured to the nearest centimetre and later slope corrected and extended by one-half of DBH to give the final radius of the crown along each of the 36 radial directions. While doing so, only the green limbs and foliage of the tree were used to determine the edge of the live crown.Dead branches, even extruding out beyond the living edge,were not viewed as part of the demarcation (Fig. 1).

Size and shape of projected crowns of sample trees

Among the 30 sample trees across the 6 thinning treatments,DBH varied from 21.4 to 81.1 cm, with a median of 52.7 cm(Fig. 2). The smallest diameter tree was in an unthinned control plot A2, while the largest was in plot F1, one of the most intensively thinned plots. Total tree height ranged from 22.0 to 54.3 m with a median of 45.0 m. These trees represented every crown dominance class from suppressed,intermediate to dominant and experienced the full range of growing spaces from the most restricted in the crowded unthinned plots to the completely free growing that were made available to individual trees through repeated thinning.As a result, the 30 sample trees had a wide range of sizes and exhibited a great deal of variability in crown shape and morphology (Fig. 2). The largest crown radius among the 36 evenly spaced radii ranged from 1.37 to 12.89 m, while the average crown radius varied from 0.79 to 7.75 m among the 30 projected crowns. The projected crown area, calculated as the sum of 36 triangle areas formed by joining the extremities of the adjacent crown radii with a straight line, varied from 2.63 to 199.46 m2with a median of 26.24 m2among the 30 sample trees.

Computation of indices and rank order correlation analysis

All 13 existing and new CAIs were computed for each projected crown using its 36 radius measurements either through programs written in R or using existing functions in two R packages that were released or updated in late 2019. The Package ‘REAT’ (Regional Economic Analysis Toolbox) Version 3.0.2 was used to compute the four new crown asymmetry indices, CAI9, CAI10, CAI11and CAI12, i.e.the adjusted Gini, Hoover, Atkinson and Theil indices for economic inequality (Wieland 2019). The Package ‘rgeos’(Interface to Geometry Engine-Open Source) Version 0.5-2 provided functions for calculating the areas and centroids of the projected crowns (Bivand et al. 2017).

After the 13 CAIs were calculated for the 30 projected crowns, their patterns of correlation were examined visually through a scatterplot matrix. The patterns were in accordance with the expected monotonic relationship between all 78 pairs of the 13 CAIs. In addition, thirteen series of rank orders were created by sorting each CAI in an ascending order to rank the crowns according to their degree of asymmetry from 1 to 30. There were no tied ranks for any CAI because of the numeric precision used for the CAI computation. As each CAI formed a different rank order, the average rank order of the 30 crowns was computed to serve the purpose of comparison. To determine the strength of the monotonic relationship and the degree of similarity between two rankings for any pair of the CAIs, Spearman’s rank order correlation coefficient (ρ) was calculated for every pair of the 13 CAIs according to the formula given in Sokal and Rohlf (1981):

where didenotes the difference between two ranks of theith projected crown and n equals 30, the total number of projected crowns. The upper triangular correlation matrix for the 13 indices was displayed using the R package ‘corrplot’of Wei et al. (2017).

Comparing CAIs over different numbers of crown radii

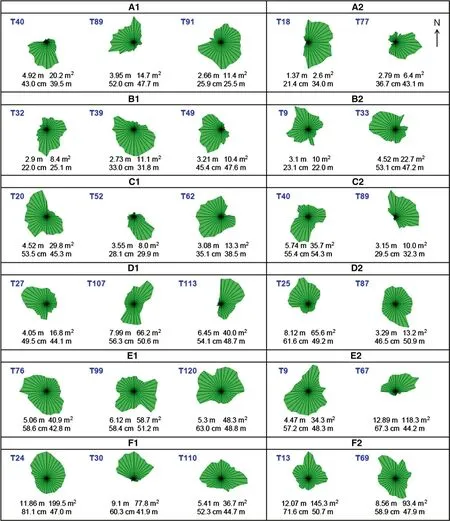
Fig. 2 Projected crowns of 30 trees sampled across six thinning treatments (a- f) in two replicates (1 and 2) of the CCT experiment.Each crown was drawn by joining the extremities of the adjacent crown radii with a straight line for all 36 evenly angularly spaced radii. The tree number of the crown is indicated by the code on its top left side. The first row of two numbers beneath each crown are its maximum radius and projected crown area, while the second row of two numbers are the DBH and total height of the tree

As previously reviewed, the number of conventionally measured radii for individual trees has mostly varied from 2 to 8, and rarely to 16 in forest research and practical applications. Across different numbers of measured crown radii(Nr,indexed byr),the calculated value of theith crown asymmetry index,CAIi(Nr), could be expected to vary for the same projected crown. Among the 13 CAIs, the most stable and consistent CAIs would have to be selected and recommended for use. In doing so, the values ofCAIi(36) ,i.e. CAIs calculated using all 36 measured radii of each projected crown, were regarded as the ‘true’ values and used to compare and benchmark the performances ofCAIi(Nr) , i.e.all CAIs across different numbers of measured crown radii.To cater for all practical applications, an increasing sequence of 8 numbers of crown radii (2, 3, 4, 5, 6, 8, 12, 16), denoted by Nrand indexed byrfrom 1 to 8, was chosen.

Fig. 3 Multi-panel display of measured and interpolated crown radii(red and black dots) plotted on a relative scale along every degree of radial direction from 1° to 360° for the 30 projected crowns. The first code in the top stripe of each penal shows the plot and tree numbers as in Fig. 2, while the second number indicates the maximum crown radius, which equals 1 on the relative scale

For each CAI and projected crown (ω) , two benchmarking statistics were used to indicate the bias and precision of the CAI calculated using each of the 8 numbers of crown radii as shown below:

Although all 13 CAIs were formulated to vary between 0 and 1, they had different ranges for the 30 projected crowns.For example, one CAI might have a maximum value of 0.09,while another could reach a maximum of 0.9, i.e. tenfold larger. To facilitate the comparisons across all CAIs, relative bias (RBiωr) and normalized RMSE (RMSEiωr) were calculated as follows:

Results

Range of CAI values and their rank order correlation based on 36 radii

The 13 CAIs calculated using all 36 measured radii of each projected crown had different ranges and degrees of variation in their index values among the 30 projected crowns(Fig. 4). The minimum index value varied from 0 for CAI12to 0.25 for CAI1, while the maximum varied between 0.09 for CAI12and 0.94 for CAI2. Correspondingly, the range in index value changed from the minimum of 0.09 in the case of CAI12to the maximum of 0.83 in the case of CAI2,with a median of 0.37 as observed for CAI5(Fig. 4). The ranges of the first three indices, CAI1, CAI2and CAI3, and the last index CAI13were all greater than 0.59, covering a larger part of the def ined [0, 1] than other CAIs. The first group of 5 existing CAIs in the forestry and ecological literature (CAI1−CAI5) generally had a wider range than the second group of 3 CAIs based on the measures of circularity for digital images (CAI6−CAI8) and the third group of 4 CAIs based on the measures of economic inequality (CAI9−CAI12). As each CAI ranked the 30 projected crowns in a different order, only the average rank order was shown for easy visual perception in comparing different rank orders (Fig. 5).

Fig. 4 Boxplots of index values for the 30 projected crowns across the 13 CAIs calculated using all 36 measured radii of each crown (left). The Spearman’s rank order correlation coefficients (ρ) of each CAI with the other 12 CAIs are also summarized in boxplots (right)

The code above each crown indicate the plot and tree numbers as in Figs. 2 and 3. The red dot within each crown area is the centroid of the projected crown.

As displayed in the graph of correlation matrix for the 13 CAIs (Fig. 6), the Spearman’s rank order correlation coefficient (ρ) varied between 0.80 and 1.00 among the 78 pairs of CAIs. The value of ρ indicated the degree of concordance between two rankings which was selectively and summarily demonstrated for easy cognition (Fig. 7). The strength of the pairwise correlation for CAIs within each group differed across the three groups as indicated by the three triangular submatrices (Fig. 6). The five existing CAIs (CAI1−CAI5) in the first group were the least correlated, with ρ ranging from 0.83 to 0.97 with an average of 0.90 for the 10 pairs. The three CAIs (CAI6−CAI8) in the second group had three ρ values ranging from 0.97 and 1.The four CAIs (CAI9−CAI12) in the third group were the most closely correlated, with the 6 ρ values lying mostly between 0.99 and 1. The strength of correlation between CAIs paired from different groups also differed as shown by the three block submatrices. The 3 CAIs in the second group and the 4 CAIs in the third group were closely correlated, with ρ ranging from 0.95 to 0.99 among the 12 pairs of across group CAIs. In comparison, the 5 existing CAIs in the first group were not as strongly correlated with CAIs in either of the two remaining groups.Although standing alone and not belonging to any of the three groups, CAI13was more consistently and closely correlated with all other 12 CAIs (Fig. 4), with ρ ranging from 0.90 to 0.98 for its correlation with the 5 CAIs in the first group, being 0.92 for its correlation with all 3 CAIs in the second group, and taking the value of either 0.93 or 0.94 for its correlation with the 4 CAIs in the third group.The average of its 12 ρ values was 0.93 (Fig. 6).

Fig. 5 Projected crowns displayed sequentially from 1 to 30 according to their average ranks ordered by the 13 CAIs

Fig. 6 Spearman’s rank order correlation matrix for the 13 CAIs. Displayed along the uncolored diagonal of the matrix are the average correlation coefficient (ρ) of the 12 ρ values for each of the 13 CAIs

Benchmark statistics for CAIs across different numbers of crown radii

The relative bias, calculated according to Eq. (18) by taking CAIi(36) as the true values for the 30 projected crowns,differed substantially in its location and variation across the 13 CAIs and the degree of difference persisted over the sequence of 8 numbers of crown radii as denoted by Nr(Fig. 8). Among the 13 CAIs, CAI13was generally the least biased as its relative bias varied within a narrow range(< 5%) around zero and its mean relative bias was less than 0.63% across all values of Nr, except for Nr=3 and Nr=5 for which it could not be computed. For the same reasons, CAI4, CAI8and CAI10were respectively the least biased out of the first group of 5 existing CAIs in the forestry and ecological literature, the second group of 3 CAIs based on the measures of circularity for digital images, and the third group of 4 CAIs based on the measures of economic inequality. The Theil index CAI12showed much greater relative bias than the 3 other CAIs based on economic inequality and it was by far the most biased among the 13 CAIs across all values of Nr(Fig. 8).

Not only was CAI13the least biased, it was also the most precise when benchmarked against CAIi(36) as shown in Eq. 19. The normalized RMSE for CAI13also varied within narrower ranges with smaller means across all values of Nrin comparison to the other 12 CAIs. Its mean NRMSE values varied between 0.27 and 0.33 and each mean was within a narrow range that varied from 0.06 to 0.08 across Nr(Fig. 9). By the same criteria, CAI4, CAI8and CAI10were the most precise indices in their respective groups. The Theil index CAI12was also by far the most imprecise among the 13 CAIs across all values of Nr(Fig. 9).

Spearman’s rank order correlation coefficient (ρ)between CAIiω(Nr)and CAIiω(36) for the 30 projected crowns was mostly smaller than 0.80 for all CAIs when Nr=2 (Fig. 10). It rose to a range largely between 0.85 and 0.95 for all CAIs except for CAI1−CAI3and CAI5when Nr=4. As Nrincreased further from 4 to 6, ρ was mostly greater than 0.95 for CAI4and CAI8−CAI13. For the remaining CAIs, except for CAI3, the correlation coeff icient was mostly greater than 0.95 only when Nr≥8.

Fig. 7 Spearman’s rank order correlation coefficient (ρ) and the corresponding degree of concordance between two rankings illustrated using five pairs of CAIs for easy visual perception. The numbers from 1 to 30 are the average rank order numbers given to the 30 projected crowns as displayed in Fig. 5. Each CAI rank-ordered the 30 crowns somewhat differently to the average rank order. For each pair of CAIs,crowns with identical average ranks are connected by a line

Variability of and correlation between and within CAIs across Nr

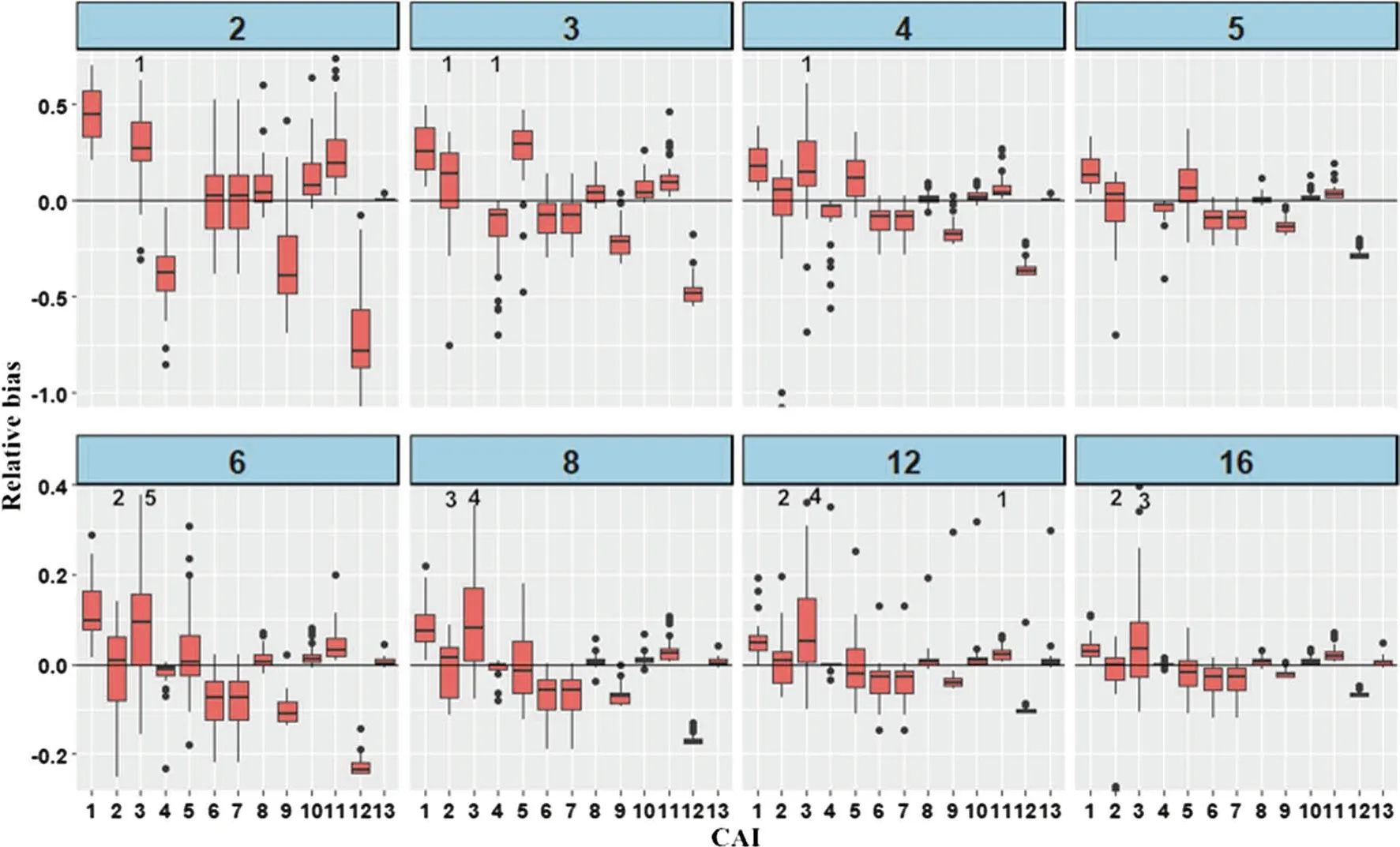
Fig. 8 Boxplots of relative bias (RBiωr) calculated in accordance with Eq. (18) for the 13 CAIs across Nr , the increasing sequence of 8 numbers of crown radii as shown in the stripe on top of each panel.All values of relative bias for CAI12 were plotted after being divided by 4 in order not to obscure other boxplots. The number on top of a boxplot indicates the number of observations with relative bias beyond the maximum of the scale

Fig. 9 Boxplots of NRMSE calculated according to Eq.(19) for the 13 CAIs across Nr , the increasing sequence of 8 numbers of crown radii as shown in the stripe on top of each panel. The number on top of a boxplot indicates the number of observations with NRMSE greater than the maximum of the scale

For each CAI, the values of RMSE calculated as per Eq. 17 increased linearly along with the average rank order of the 30 projected crowns as shown in Fig. 5 until a sharper increase for the two or three most asymmetric crowns at the end of the rank order. At the same time, RMSE decreased as Nr, the number of radii used in calculating the CAIs, increased from 2 to 16. Such trend was shown for the four least biased and most consistent CAIs, led by CAI13and followed by CAI4,CAI8and CAI10, as examples (Fig. 11). In the case of CAI13,the RMSE increased from 0.06 for the least asymmetric crown to 0.28 for the most asymmetric crown when Nr=2 .The change was nearly fourfold. When Nr= 4, 6, 8, 12 and 16, the RMSE increased from 0.03 to 0.15, 0.02 to 0.09, 0.01 to 0.06 0.01 to 0.03 and 0.002 to 0.03 respectively along the average rank order of the 30 projected crowns. These increases were largely between three and sixfold, except for the extreme case of Nr= 16, for which the increase amounted to more than 12-fold. For CAI4, CAI8and CAI10, the increases in RMSE over the complete rank order of crown asymmetry for different numbers of crown radii were mostly within the same range of magnitude as observed for CAI13.

Fig.10 Boxplots of Spearman’s rank order correlation coefficient(ρ) between pairs of CAIi(Nr) and CAIi(36) for the 13 CAIs across Nr,the increasing sequence of 8 numbers of crown radii as shown in the stripe on top of each panel. The horizontal line across each panel indicates the ρv alue of 0.95

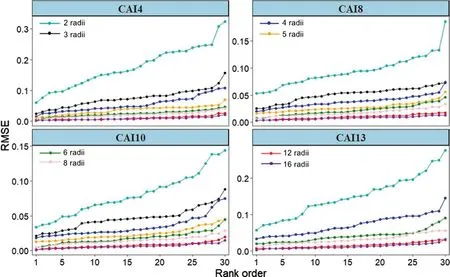
Fig. 11 RMSE in relation to rank order for each of the four best performing CAIs that were calculated respectively using different numbers of crown radii as indicated by the legends inside the four plots. The rank order for each CAI was based on the index values calculated using all 36 measured crown radii of each projected crown

The 4 best performing CAIs had relatively high pairwise rank order correlation across Nras indicated by theircorrelation matrices (Fig. 12). When Nr= 2, these four CAIs are mathematically equivalent as can be easily deduced, so the ρ values in the correlation matrix were all equal to 1. For other values of Nr, the degree of correlation differed slightly among the six pairs of CAIs. The pair of CAI8and CAI10was the most closely correlated as their ρ values across Nrwere all 0.99, which was followed by the pair of CAI13and CAI4with ρ values ranging between 0.96 and 0.98. For each CAI,the ρ values in lower part of the upper triangular 9 × 9 matrix corresponding to the cross correlation for Nrgreater than 6 were mostly greater than 0.95 (Fig. 13). In comparison, the 6 ρ values in the third row of each matrix, corresponding to

the correlations betweenCAIiω(4) andCAIiωNr>4 were generally between 0.8 and 0.9.

Fig. 12 Spearman’s rank order correlation matrix for the four best performing CAIs across Nr ,the 8 numbers of crown radii as indicated in the top stripe of each panel. For Nr equals 3 and 5, the last column of the correlation matrix was given zero values as CAI13 cannot be calculated when Nr is an odd number

Fig. 13 Spearman’s rank order correlation matrix for each of the four best performing CAIs

The column and row numbers indicate the number of crown radiiNrthat were used in the CAI calculations.Two rows and two columns in the correlation matrix forCAI13were given zero values as the index cannot be calculated whenNrequals 3 and 5.

Discussion

Crown asymmetry and indices thereof have been the subject of attention in forest and ecological research over the past 50 years. During this time several CAIs have been constructed by researchers often on an ad hoc basis to address specific objectives related to tree growth and competition,stand dynamics, stem form, crown structure and treefall risks(Curtin 1970; Kio 1970; Franco 1986; Young and Hubbell 1991; Young and Perkocha 1994; Umeki 1995a; Lei et al.2012). Although sharing some similarities, these existing indices differ not only in the scale but also in the direction of their values in indicating the degree of crown asymmetry.These differences render results from different studies based on varying numbers of crown radius measurements noncomparable. This study represented the first attempt at devising normative measures of crown asymmetry to overcome such noncomparability in studies on and applications of crown asymmetry.

Among the 13 CAIs evaluated, CAI13, the simple measure for the bilateral symmetry ofleaves proposed by Shi et al.(2018), was found to be the least biased and most precise across different numbers of measured crown radii (Nr) based on its benchmarking statistics. It was also most consistently and closely correlated with the other 12 CAIs as indicated by the values of Spearman’s rank order correlation coefficient(ρ). The narrow range of its 12 ρ values and their mean of 0.93 in Fig. 6 suggested that it had a greater degree of commonality with all other CAIs than any other CAI in rank ordering the 30 projected crowns. Because it is based on the bilateral symmetry of pairs of radii measured on the direct opposite sides of the projected crown, CAI13tended to rank a crown as highly symmetric even when its projected shape clearly departed from circularity and took a more rectangular or oblong shape but its centroid still centred around the tree trunk. The 12th tree in the average rank order of the 30 projected crowns shown in Fig. 5 was ranked the third by CAI13but the 19th by CAI8(Fig. 7), the best of the three CAIs based on the measures of circularity for digital images.This feature of CAI13is particularly worth noting when the CAIs are considered for trees grown in plantations with rectangular initial spacing as their crown shape could become regularly elliptical in the rectangular growing spaces (e.g.Sharma et al. 2002). Another feature of CAI13also arising from its bilateral symmetry formulation is that it is limited to crown radius measurements taken in pairs. When crown radii are in odd numbers, such as 3 and 5 in this case, it cannot be applied, which may limit its general application in certain, but likely rare, circumstances.

The performance of CAI13was closely followed by that of CAI4, CAI8and CAI10, respective representatives of each of the three groups of CAIs. It came as no surprise that CAI4was the best performer in the group of 5 existing CAIs because its formulation by Franco (1986) appeared to be the most well-thought-out mathematically among the five CAIs.Although proposed originally as a more general approach to the analysis of growth and form of competing modular organisms, but not explicitly and exclusively for measuring crown asymmetry, this index proved to be an effective alternative measure of crown asymmetry as indicated by its benchmarking statistics (Figs. 8 and 9). With a ρ value of 0.98 (Fig. 6), its ranking order for the 30 projected crowns was the most closely correlated with that of CAI13among the first 12 CAIs when all 36 radii were used in the calculations.The strength of the rank order correlation was equally so for other numbers of Nr(Fig. 12). Because CAI4was formulated to convert the polar coordinates of multiple crown radii into the Cartesian coordinates of a single point in a Euclidean space by summing up weighted radii that were projected respectively onto the x and y axes (Eq. 4), it measures the symmetry of a projected crown around the tree trunk through a standardized vector. Therefore, it shares the feature with CAI13and gave the same rank (3rd) to the oblong shaped crown that was centred around the tree trunk (Fig. 7). As a standardized vector within a unit reference circle joining the centre position at tree trunk with the centroid of the projected crown, CAI4has an added advantage over CAI13in indicating not only the degree but also the direction of crown asymmetry. This added advantage would be particularly useful if CAI4were used for evaluating the risk of treefalls(e.g. Young and Hubbell 1991, Young and Perkocha 1994),examining neighbourhood competition among individual trees (e.g. Brisson 2001; Seidel et al. 2011; Vovides et al.2018), and depicting spatial canopy and stand dynamics (e.g.Umeki 1995a, b; Aakala et al. 2016). The reason it has been little used may be that it was not originally proposed explicitly as a crown asymmetry index and thus has received little exposure in the forestry and ecological literature.

Among the second group of 3 CAIs that were adapted from the measures of circularity for digital images, CAI8performed better than the other two variance-based CAIs, CAI6and CAI7, which had much larger relative bias and greater degree of variability than CAI8as shown by the benchmarking statistics across Nrin Figs. 8 and 9. These comparative results presented a clear case that the variance-based CAIs are not suitable for measuring crown asymmetry as variance estimation is biased and not reliable for very small samples such as the varying numbers of crown radii measured in practice. Breunig and Hutchinson (2008) provided correction factors for variance-based measures of inequality for small samples. However, the derivation of these factors seems more involved than calculating the indices themselves, making it an impractical option for the variancebased CAIs.

The very small sample size also posed some complications for CAI9, CAI11, and CAI12, the corrected Gini, the Atkinson and the Theil index. Although all are well-established and widely-used measures of income inequality in economics, their calculations are usually based on very large sample sizes representing the population of an entire region or the whole country (Greselin and Pasquazzi 2009; Chattopadhyay and De 2016). For very small sample sizes such as those represented by Nrin this case, the value of N∕(N−1) ,the bias correction factor for the Gini coefficient, decreased from 2 when Nr=2 to 1.2 when Nr=6 and to 1.07 once Nrreached 16. Such changes may introduce an additional variation in the value of CAI9across Nr. The correction factor was demonstrated statistically to be effective for small samples(Deltas 2003), but its effectiveness for very small samples remains to be evaluated. Both the Atkinson and the Theil index belong to a general class of entropy-based measures of inequality. But as similarly found by Breunig and Hutchinson (2008), the special case of the Atkinson index (CAI11)exhibited much less small sample bias than the Theil index(CAI12) (Fig. 8). Approximate bias correction factors were also derived for the Atkinson and the Theil index through Taylor’s series approximation for small and very small samples of only several observations (Giles 2005; Breunig and Hutchinson 2008; Ferrante and Pacei 2019). However, the approximate bias correction is not without its own problems since the decreased bias was shown to be more than compensated for by increased variance after correction (Breunig and Hutchinson 2008). Besides, the approximation is practically far too complicated for our purpose of devising simple measures of crown asymmetry. These complications will potentially make it difficult to compare values of the same index across Nr, although the rank orders of the projected crowns could still be closely correlated for the index when Nr>4,like the pattern of correlation for the four best performing CAIs in Fig. 13. The degree of difficulty differs among CAI9,CAI11, and CAI12, but the difficulty was not shared by the Hoover index, CAI10, as shown by the benchmarking statistics (Figs. 8 and 9). It was not only the best performing but also the simplest to calculate among the four CAIs based on measures of economic inequality.

The four best performing CAIs should provide the basis for a more normative measure of crown asymmetry in both forest research and management. If the best performer(CAI13) is not an ideal option for some practical reason in an application, CAI4, CAI8and CAI10will serve as the best alternatives. However, no matter which CAI is chosen, the minimum number of crown radii that is needed to provide at least an indicative measure of crown asymmetry is four as shown by the correlation matrices in Fig. 13. For more accurate and consistent measures of crown asymmetry, at least 6 or 8 crown radii are needed in the CAI calculations. At the same time, the range of variability in crown morphology of the trees under investigation will also need to be considered.For example, angiosperm species tend to show more crown asymmetry due to their more modular crown architecture than gymnosperms (Getzin and Wiegand 2007; Hastings et al. 2020). Regularly spaced plantations trees are likely to have more symmetric crowns than mature or over-mature trees in natural forests. As shown by the patterns of RMSE of the 4 best performing CAIs along the rank order of the 30 crowns (Fig. 11), a larger number of radii will be needed to rank order more asymmetric crowns with the same degree of consistency that can be achieved with a smaller number of radii for less asymmetric crowns.

A more normative measure of crown asymmetry, a characteristic attribute of crown morphology, will have valuable applications in modelling the stand dynamics, thinning responses, and the growth and yield of forest stands.Although the CAIs are based on projected crown radii in a 2-dimensional place, they can be readily extended to other crown variables extracted from LiDAR and other remotely sensed data such as the point cloud density, volume and estimated biomass in different semi-quadrants of a 3-dimensional crown. When incorporated into individual tree and crown metrics that are now commonly extracted from LiDAR data and remote sensing images (Seidel et al.2011; Olivier et al. 2016; Pont 2016; Trochta et al. 2017;Krůček et al. 2019), this additional metric will also facilitate the process of big data analytics and artificial intelligence in forestry wherever crown morphology is among the factors to be considered for management decision making.

AcknowledgementsThis article was written in the memory of the late Dr. Richard A. Curtin, a pioneer scientist on the growth and stand dynamics of eucalypt trees and forests, who designed and established this blackbutt CCT experiments in 1964. Dr. Christine Stone provided helpful comments.

Open AccessThis article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source,provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creat iveco mmons.org/licen ses/by/4.0/.