基于遗传算法的除雪机螺旋集雪器结构优化研究

王 超，李大胜，范恒亮

(蚌埠学院 机械与车辆工程学院，安徽 蚌埠 233030)

除雪机是北方地区常见的冬季道路养护设备之一，它在进行除雪作业时，最主要的任务就是快速高效地清除路面积雪，保障道路交通安全[1]。除雪机的核心作业装置为集雪装置和抛雪装置，集雪装置的作用是通过螺旋式集雪器将积雪集中起来，然后传送至抛雪装置内抛出[2]，螺旋式集雪器结构如图1所示。

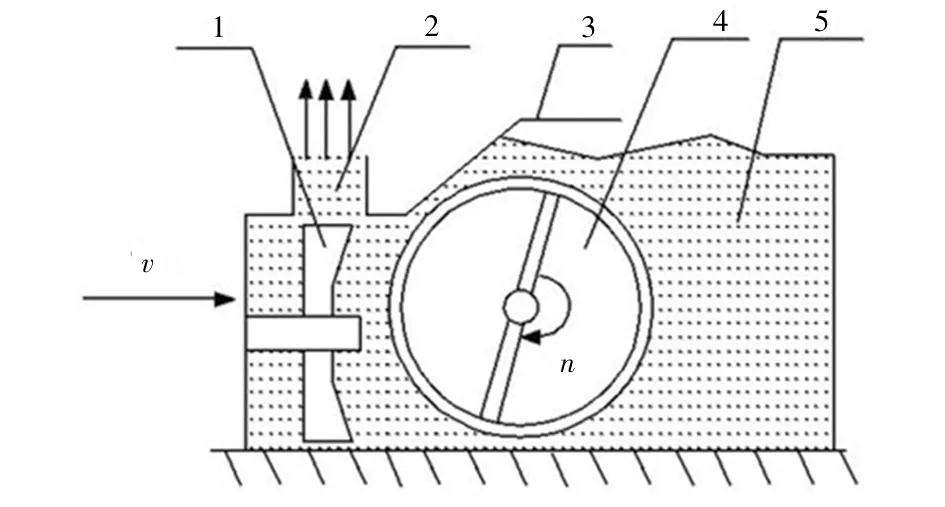
1—抛雪叶片；2—抛雪口；3—挡板；4—螺旋集雪器；5—积雪；v—除雪机行走速度；n—螺旋转速。图1 螺旋集雪器结构示意图Fig 1 Structural diagram of spiral snow collector

1 现有产品参数及分析

1.1 现有产品及参数

沈阳某科技公司的小型除雪机如图2所示，其螺旋集雪器参数如表1所示。

a 除雪机

b 螺旋集雪器图2 某型号小型除雪机及其螺旋集雪器Fig 2 A certain model of small snow removal machine and its spiral snow collector

表1 螺旋集雪器参数Table 1 Parameters of spiral snow collector

由图2可知，该除雪机的螺旋集雪器由6个单片螺旋叶片组成，其中每3个叶片组成1组，2组成镜像排列。

1.2 螺旋集雪器运动分析

从右侧观察，集雪器工作时螺旋叶片呈逆时针转动，以除雪机正面左侧螺旋叶片为例，雪粒在螺旋叶片上的受力情况分析如图3所示。原点处的雪粒在叶片转动时受到摩擦力f以及螺旋曲面法向作用力N，两者形成合力F。合力F又可以分解为轴向作用力Fs和周向作用力Fz，其中雪粒主要受到轴向作用力Fs的作用，即螺旋集雪器工作时，雪粒通过螺旋叶片从螺旋左右两端向中间集中。

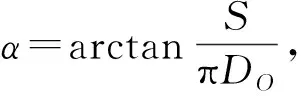
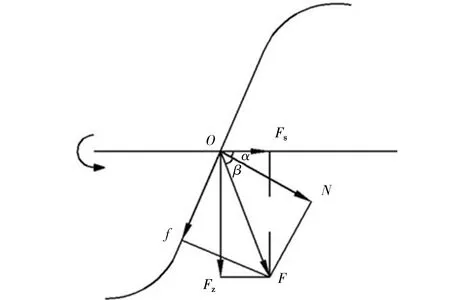
图3 雪粒在螺旋集雪器上的受力分析Fig 3 Force analysis of snow grains on the spiral snow collector

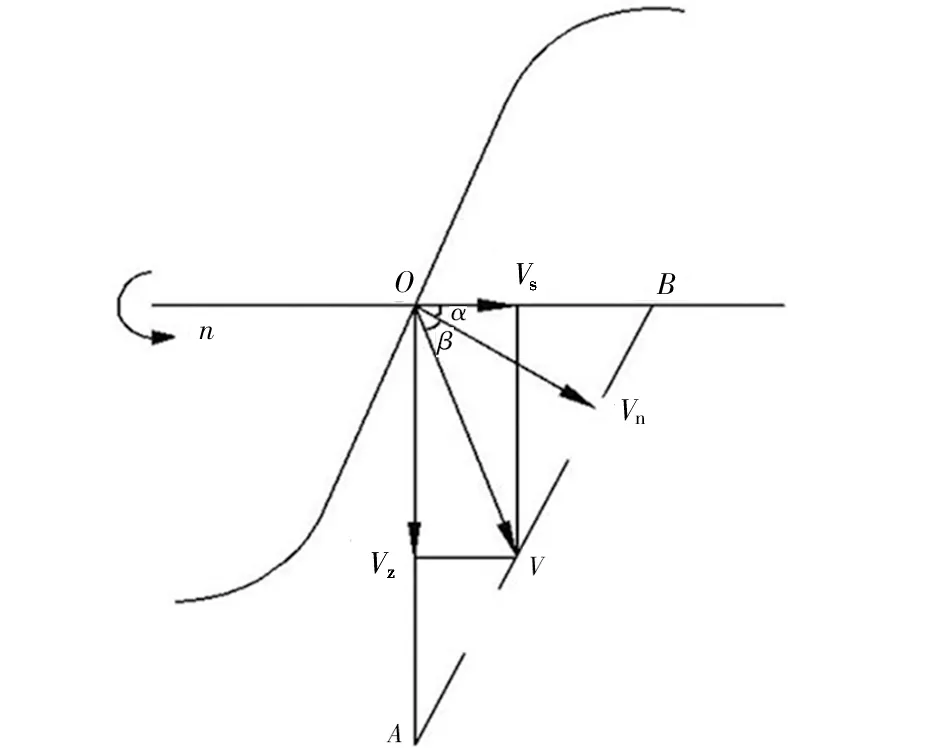
图4 雪粒在螺旋集雪器上的运动分析Fig 4 Motion analysis of snow grains on the spiral snow collector

由图4可知拟合速度V又可以分解为轴向运动速度Vs和周向运动速度Vz。

1.3 螺旋集雪器生产率计算

除雪机优化设计的关键之一是提高螺旋集雪器的生产率。螺旋集雪器的生产率(Q)，指的是螺旋集雪器清除积雪的效率，即单位时间内螺旋集雪器所能传送的积雪的体积，其计算公式如下：

Q=ZVs

式中：Z为切雪断层横断面面积，m2；Vs为螺旋集雪器工作时的轴向运动速度，m/s;D为螺旋集雪器螺旋叶片外径，m；d为螺旋集雪器螺旋叶片内径，m；Kd为积雪的填充系数，取值0.93；σ为螺旋叶片外边缘与除雪机机身壳体间隙，一般取值0.005～0.015 m，通过对产品外壳实测后，选取σ值为0.01 m。

式中：S为螺旋螺距，m；n为螺旋转速，r/min。

不过由于轴向运动速度Vs是伴随着雪颗粒所在螺旋的半径位置的变化而变化的，其值无法具体固定下来，所以采用简化算法，如下式：

即螺旋集雪器生产率

1.4 螺旋集雪器使用功率计算

螺旋集雪器的使用功率P计算公式为[4]：

0.013 3μsinδcosδ]× 0.075×K1FpQ1

式中：Vx为除雪机自行走速度，2～5 km/h，即0.56～1.39 m/s。S为螺旋螺距，m。D，d为螺旋外径,螺旋内径，m。n为螺旋转速，r/min。μ为螺旋与雪之间的摩擦因数，μ=0.12。K1为螺旋形状系数，K1=0.6。Q1为除雪机理论除雪体积，Q1=Vxhb，m3。h为除雪机除雪高度，m。b为除雪机除雪宽度，m。Fp为雪压缩破坏阻力，Fp=24(ρ-140)g，N/m3。ρ为雪的密度，kg/m3，此处考虑到清雪时的各种情况，选取ρ=500 kg/m3。δ为螺旋排雪当量角，tanδ=Vx/u。u为螺旋轴向进给速度，u=S·n/60，m/s。

2 遗传算法优化分析

2.1 遗传算法简介

遗传算法是一种借鉴生物界自然选择和自然遗传机制的随机算法[5]。MATLAB软件中内嵌的遗传算法工具箱对使用遗传算法进行优化求解给予了良好的支持，其一般步骤如下[6]：

(1)确定适应度函数，即建立目标函数。求解时通常将目标函数的求解转换为求函数最小值的问题。

(2)确定目标函数中独立变量的个数，及每个独立变量的约束条件。

(3)通过以上条件，编写目标函数的MATLAB文件。

(4)进入MATLAB遗传算法工具箱，调用之前编写好的MATLAB文件，设置群体大小范围、终止进化代数、交叉概率、变异概率等参数后，即可运行遗传算法求解。

2.2 螺旋集雪器优化目标函数的建立

对螺旋集雪器的性能进行优化分析时，需要使其除雪效率，即生产率越大越好，同时，也要尽量降低集雪器的使用功率。遗传算法工具箱一般用于求解最小值问题，因此，可通过螺旋集雪器生产率及使用功率计算公式的整合，将对螺旋集雪器性能的优化求解简化为对P/Q最小值的求解。

2.3 目标函数中独立变量的确定

对螺旋集雪器性能有影响的参数分别为螺旋叶片螺距S，螺旋叶片内径d，螺旋叶片外径D，以及螺旋叶片工作转速n。由于转速的设计和结构相关，且单纯用提高转速的方法来增加雪粒的运动速度没有实际意义，所以n不做变化。依次以螺距、螺旋内径和螺旋外径做变量，观察它们的改变与P/Q值大小的关系，如图5所示。

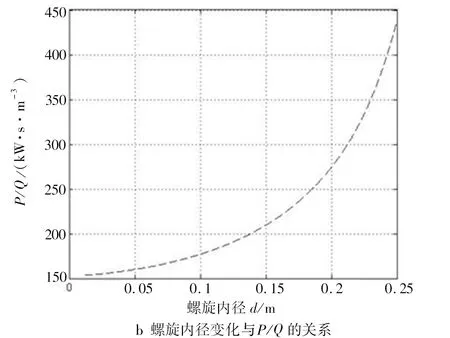
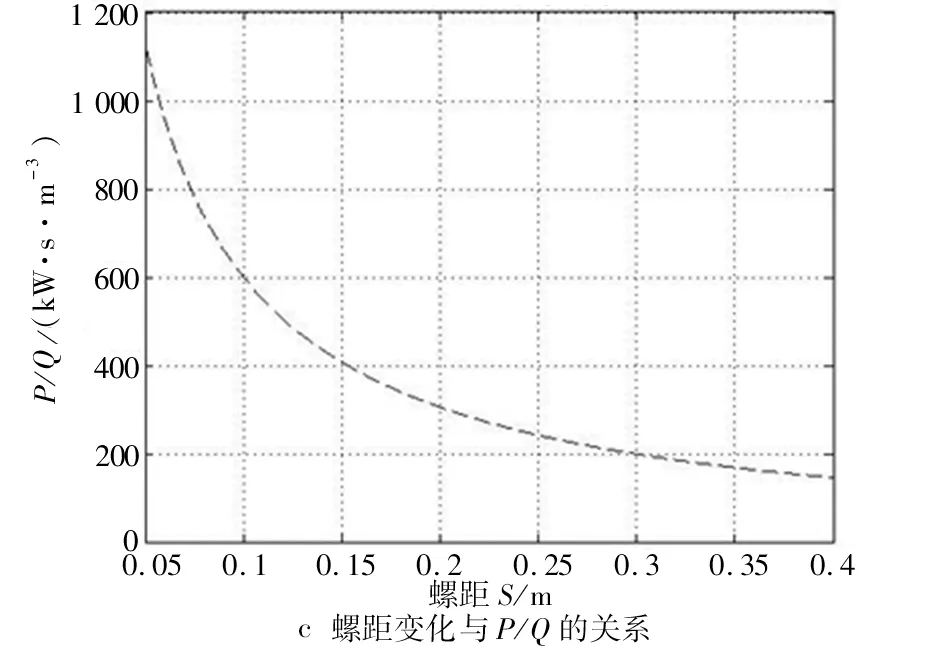
图5 各参数与P/Q值的关系Fig 5 Relation between each parameter and P/Q value

由图5可知，螺旋外径D在0.25～0.4 m间变化时，P/Q值下降了约62.5%；螺旋内径d在0.1～0.25 m间变化时，P/Q值上升了约144.44%；螺旋螺距S在0.1～0.3 m间变化时，P/Q值下降了约66.67%。可见3个参数的变化对优化结果的影响都十分显著，但是由于产品整体框架的限制，需要保持螺旋外径D不变，因而，选取螺旋内径d以及螺旋螺距S为目标函数中的独立变量。

2.4 目标函数的遗传算法求解

对目标函数求解之前有4个运行参数需要预先设定，分别为M，T，Pc，Pm。M为群体大小，即群体中所含个体的数量，一般取值为20～100，考虑到设计变量的取值范围较为广泛，本文需要较大的群体，因而取值80；T为遗传算法的终止进化代数，一般取值100～500，为了防止目标函数在求解时过早收敛，本文取值150；Pc为交叉概率，一般取值0.4～0.99，为了增加求解结果的准确性，需要较大的交叉概率值，本文取值0.8；Pm为变异概率，一般取值为0.000 1～0.1，较大的变异概率可以防止局部最优解的出现，即减小提前收敛的可能，故本文选取的变异概率为0.005。

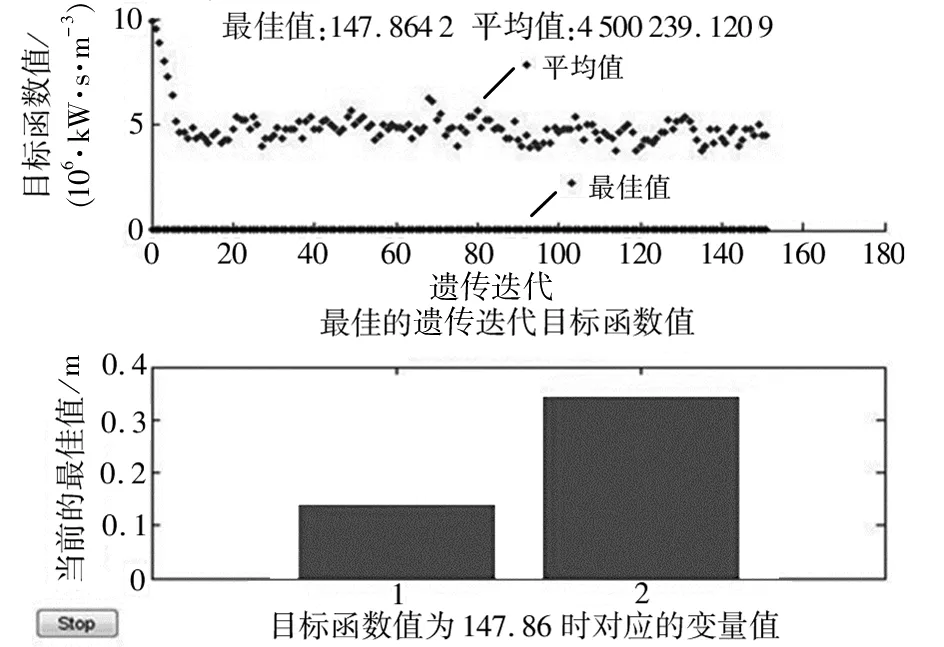
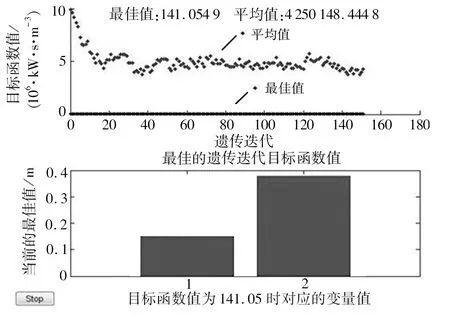
设定好参数后，选择之前按照目标函数及变量约束条件编制的MATLAB文件，变量数为2个，设置后开始运算。因为遗传算法的种群是随机选取的，所以运算显示过程并不唯一，结果也不是完全相同，但经多次运算实验后，目标函数值会稳定在一定范围内，结果如图6所示。

由图6可知，经过多次运算，目标函数的值在遗传进行到20代左右时逐渐稳定，经过150代的遗传选择计算，其最优值最终稳定在140左右，设计变量取值及优化结果见表2。

a

b

c

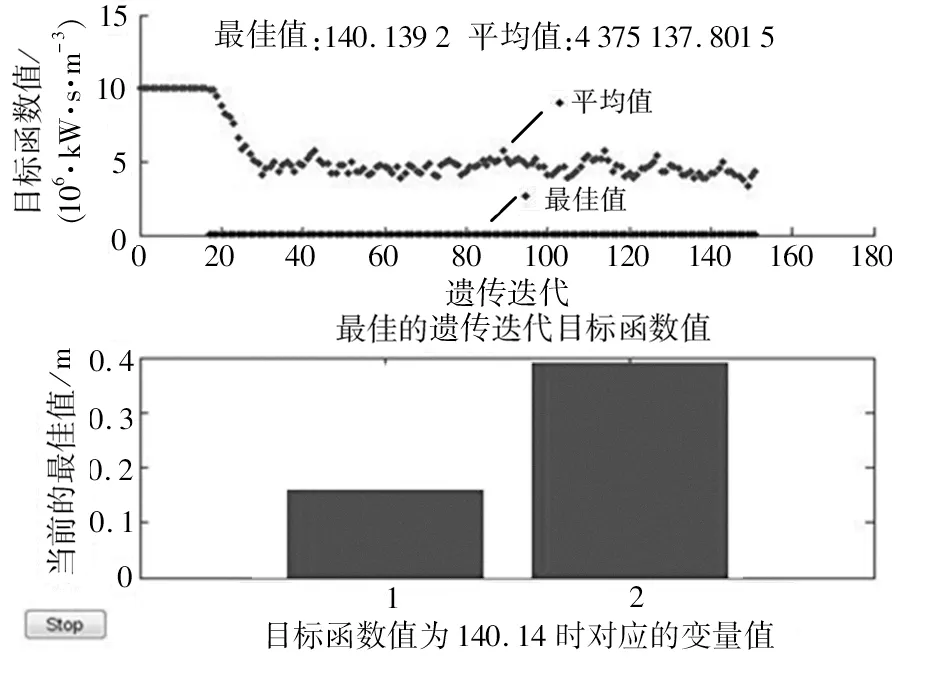
d图6 MATLAB遗传算法优化结果Fig 6 Optimization results of MATLAB genetic algorithm

从表2可以看出，在目标函数值趋近140时，d(1)值趋近于0.16 m，S(2)值趋近于0.39 m，所以可初步确定优化解为螺旋内径d减小到160 mm，螺旋螺距S增加到390 mm。但是如图7所示，螺距过大会使轴向运动距离减小，且周向运动速度与轴向运动速度过于接近，不利于螺旋集雪器的高效工作，综合考虑选取螺距S为300 mm。因此设计优化方案的螺旋内径为160 mm，螺旋螺距为300 mm。

表2 MATLAB遗传算法优化结果Table 2 Optimization results of MATLAB genetic algorithm

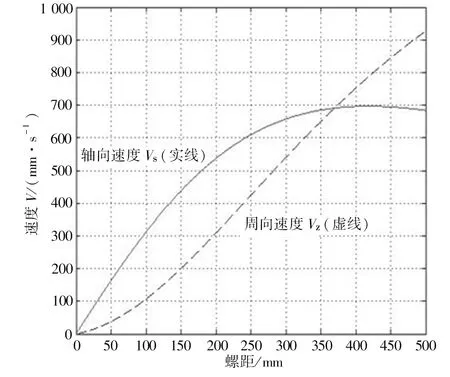
图7 直径固定时，螺距与运动速度的关系Fig 7 Relation between pitch and velocity at fixed diameter

3 优化方案与原有方案性能对比

优化方案与原有方案性能对比如表3所示。由表3可知，优化后使用功率降低3.09%，除雪生产率增加64.52%，优化效果良好。

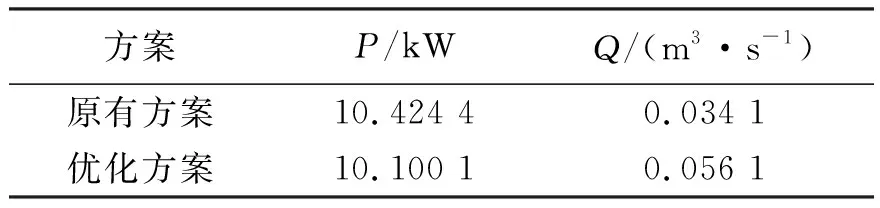
表3 优化方案与原有方案性能对比Table 3 Performance comparison between optimization scheme and original scheme

4 结论

文章分析了雪粒在现有产品螺旋集雪器上的受力及运动情况，列出了螺旋集雪器生产率及使用功率的计算方法。在此基础上，进一步分析了螺旋集雪器的结构参数，按照遗传算法的相关原理及分析步骤，选出了对螺旋集雪器性能影响较大的2个变量，分别为螺旋内径和螺距。最后利用MATLAB软件遗传算法工具箱求解最优解，将结果修正后得到优化方案。