基于自适应牵制控制的时变时滞复杂网络同步

马益聪，邰亚丽

(1.集美大学 理学院，福建 厦门 361021；2.集美大学 诚毅学院，福建 厦门 361021)

复杂网络广泛存在于自然界与人类社会的各种现象中，引起了人们的广泛关注。复杂网络中的时滞包括节点时滞和耦合时滞，已经成为影响复杂网络同步及同步控制的重要因素。人们曾试图将应用于混沌系统的脉冲控制[1-3]、自适应控制方法[4-5]以及它们之间的组合[6-7]运用于复杂的网络系统，将网络中的每个节点加入控制器，以达到对网络的全局控制，但实现起来较为困难。为此，Li等[8]提出将牵制控制的思想用于复杂网络的同步，其控制思想是控制系统的部分节点，通过节点间的相互作用，达到控制整个网络，使系统达到同步的目的。

本文研究节点含时变时滞的连续时间线性耗散耦合网络全局指数渐近同步控制问题，通过给部分节点添加自适应牵制控制器实现网络的同步，得到网络的同步准则；所设计的控制器能够节约控制成本且易于实现，数值仿真结果也证实了该控制器的有效性。

1 网络模型及预备条件

考虑由N个具有时变时滞的节点构成的复杂网络

i=1,2,...,N

(1)

式中：xi(t)=(xi1(t),xi2(t),...,xin(t))T∈n是第i个节点的状态变量；f(·,·)是非线性连续可微的向量函数；τ(t)是节点时变时滞；aij是从节点j到节点i的耦合强度，矩阵A=(aij)∈N×N表示网络连接的耦合矩阵，如果节点i与节点j之间有连接，则aij>0，否则aij=0(i≠j)，且对角元素矩阵G∈n×n是内连耦合常数矩阵；ui∈n是待设计的网络节点控制器。

假设1 若函数f(·,·)满足一致Lipschitz条件，即对于任意xi(t)=(xi1(t),xi2(t),...,

xin(t))T、s(t)=(s1(t),s2(t),...,sn(t))T，总存在正常数L1,L2>0，使得

(xi(t)-s(t))[f(xi(t),xi(t-τ(t)))-

f(s(t),s(t-τ(t)))]

≤L1‖xi(t)-s(t)‖2+

L2‖xi(t-τ(t))-s(t-τ(t))‖2,

i=1,2,...,N.

(2)

成立，其中‖·‖表示欧几里得范数。

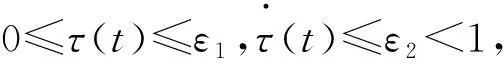
2 控制器设计及同步分析

令复杂动力学网络(1)与孤立节点的误差ei(t)=xi(t)-s(t)，i=1,2,...,N， 则误差状态方程为：

f(xi(t),xi(t-τ(t)))-f(s(t),s(t-τ(t)))+

(3)

式中ei(t)=(ei1(t),ei2(t),...,ein(t))T。

定义2 如果存在常数P>0、α>0，使得对于任意初始条件，有‖ei(t)‖≤Pexp(-αt)，i=1,2,

...,N，则称网络(1)是全局指数同步的。

下文将设计合适的自适应牵制网络节点控制器ui∈n，使任意初始状态的复杂网络(1)实现全局指数渐近同步。

现给出自适应牵制控制器ui(t)的定义，并选择前l个节点进行控制，具体如下：

μ>0,δi>0

(4)

式中di为控制器增益，δi为控制器增益参数。

这时误差状态方程(3)可变为：

(5)

引理1[9](Schur补定理)：

(2)A(x)<0且C(x)-BT(x)A-1(x)B(x)<0；

(3)C(x)<0且A(x)-B(x)C-1(x)·BT(x)<0

式中:如果AT(x)=A(x),CT(x)=C(x),则上述(1)、(2)、(3)等价。

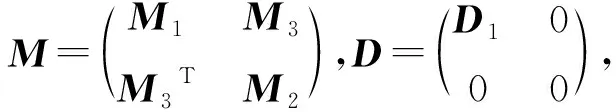
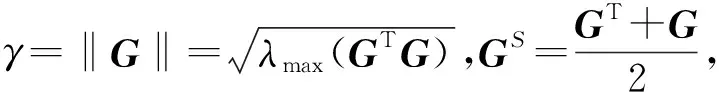
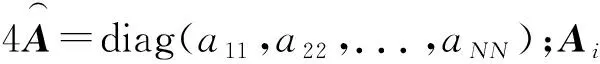
主要结果由下面的定理给出。

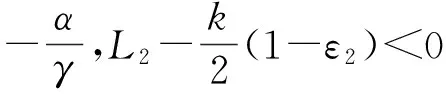
证明：构造Lyapunov函数

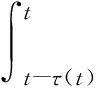
对V(t)求导，并利用不等式xTy≤|xTy|≤

‖x‖‖y‖,得

W1+W2+W3

利用假设1、假设2及式(5),得

‖ei(t-τ(t))‖2(1-ε2))]exp(μt)

经整理得，

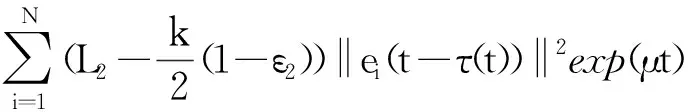
式中e=(‖e1‖,‖e2‖,...,‖eN‖)T。

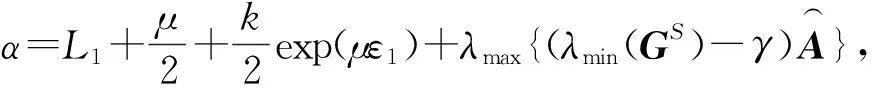
3 数值仿真

为了验证定理1的有效性，考虑N=20的复杂网络，网络节点是如下的时滞Chua系统[11]。

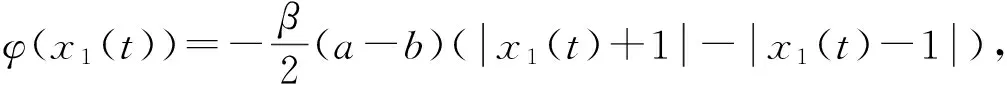
可以验证当L1=12.68,L2=0.25时，非线性函数f(·，·)满足假设1的条件，此时该时滞Chua系统是混沌的，外部耦合矩阵取

内部耦合矩阵为

图1为网络各个节点在不施加控制器时的误差状态运动曲线。由图1可知，网络自身无法达到同步。

利用MATLAB易知γ=‖G‖=4.788,取μ=0.2,k=0.8,ε1=0.1,ε2=0.2,经计算得

显然，存在常数l=8满足λ9=-6.240 6<

图2给出了网络的前8个节点施加文中自适应牵制控制器后的同步误差ei1(t)、ei2(t)、ei3(t),i=1,2,...,20的演化曲线。由图2可以看出，系统在自适应牵制控制下很快实现了同步。显然，通过对网络中的一小部分节点施加控制器来实现控制整个网络既节约了成本又能够易于实现。

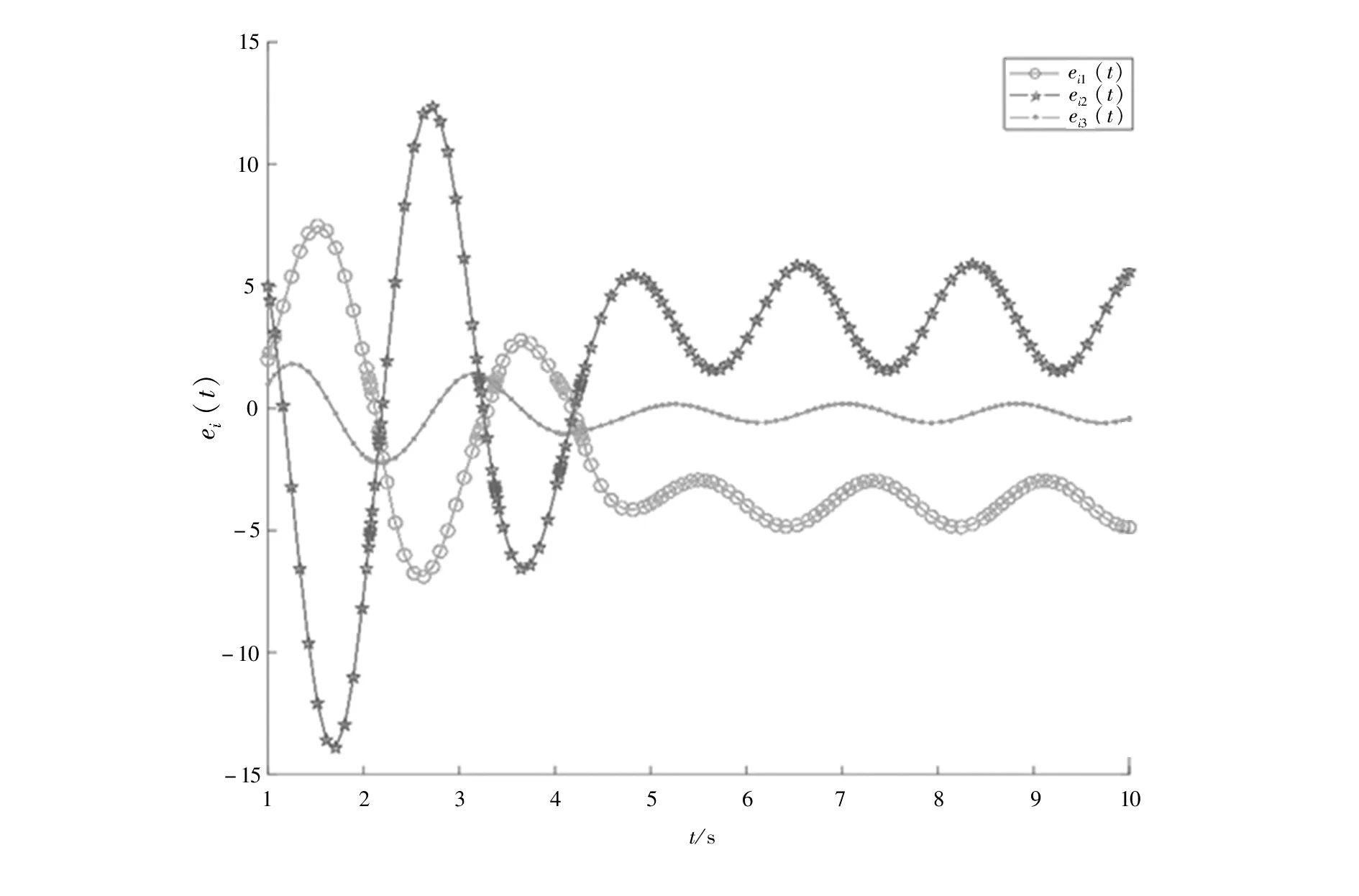
图1 节点未施加控制器时误差系统的状态曲线Fig 1 The state curve of the error system when no controller is applied to the node

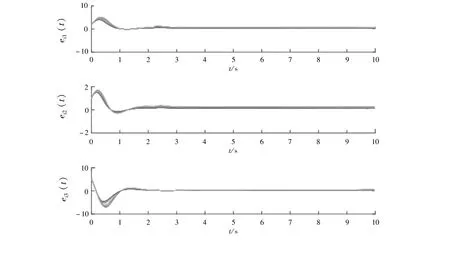
图2 前8个节点施加控制器后误差系统的演化曲线Fig 2 The evolution curve of the error system after the controller is applied to the first 8 nodes

4 结语

针对一类节点含时变时滞的复杂网络模型的同步问题，设计了一个自适应牵制控制器，对复杂网络的部分节点实施牵制控制；构造适当的Lyapunov函数使网络达到全局指数渐近同步的充分条件；最后通过数值仿真验证了文中方法的有效性。