DCB对精密单点定位中的精度影响分析

丁 楠,殷立琼

(江苏省基础地理信息中心，江苏 南京 210013)

精密单点定位(Precise Point Positioning,PPP)是指仅采用一台双频接收器，通过地面站的卫星观测数据计算精密卫星轨道参数与卫星钟差参数[1-2]，结合精密星历及精密钟差，即可在全球任意地点进行高精度定位。相较于相对定位，精密单点定位采用一个工作站即可工作，摆脱了基线的约束，得到了广泛的应用。但是GNSS(Global Navigation Satellite System)观测经常受到GNSS卫星和用户接收机的硬件影响而产生传输偏差，导致信息延迟与定位不准。其中，接收机的硬件延迟主要包含差分码偏差(Differential Code Bias，DCB)和差分相位偏差(Differential Phase Bias，DPB)[3]。

接收机的差分码偏差(DCB)是指卫星接收机同频率信号所产生的延迟，是影响定位精度的主要误差源，该误差主要由电离层中的电子含量所引起[4]。目前，国内外研究者在对DCB的研究中，通常忽略其可能存在的波动，即假设接收机DCB在一段时间内保持稳定[5-6]。本文在PPP定位误差的基础上，加入了DCB误差的影响，通过实验获取站点的三维坐标，并与SINEX周解数据提供的三维坐标进行对比，分析DCB对PPP定位精度的影响。

1 精密单点定位数学模型

相较于载波相对定位，PPP的模型更为复杂，代估参数更多[7]。为简单计，这里只讨论非差非组合精密单点定位方式，它可以直接将GNSS原始观测值作为基本观测量，把站星视线方向的电离层延迟同其他参数一起进行求解[4]，方程如下：

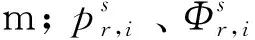
由于非差非模型直接采用IGS发布的精密钟差产品来处理卫星钟差，因此在进行数据处理时，必须考虑精密钟差包含的无电离层组合中卫星硬件的延迟量[8]，即

无电离层组合接收机端硬件延迟误差dr,if与频率无关，仅与接收机有关，因此，可将其附加入接收机钟差中一起进行估计，即

cδrI=cδr+dr,if

结合上述公式，观测方程可简化为：

2 实验结果与分析

采用Bernese软件对采集的GNSS实验数据进行精密单点定位解算[9-10]。Bernese软件是由瑞士伯尔尼大学天文研究所研制，专门用来处理GNSS数据的一款软件。Bernese软件模块条理清晰、功能强大、界面友好、操作简单，既能进行精密单点定位又能进行基线解算，对于大观测量的数据解算来说，具有运算速度快、质量优的特点，且该软件适用于多种操作系统。因此，采用该软件对IGS观测站BFJS站2019年1月1日的观测数据进行精密单点定位解算。

实验时采样历元为30 s，采用发布的SINEX周解数据作为真值，三维坐标(X,Y,Z)=(-2 148 744.520 651 02,4 426 641.165 073 59,

4 044 655.808 330 66)，实验结果如图1、图2所示。

a X方向

b Y方向

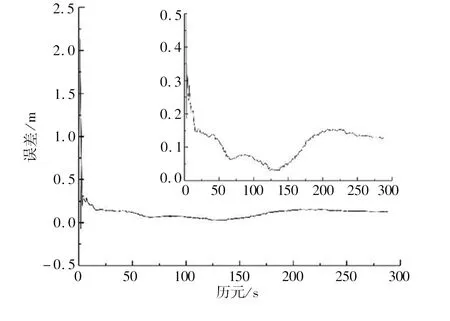
c Z方向图1 未考虑DCB的X、Y、Z方向的定位误差变化Fig 1 The variation of the positioning error in the X, Y and Z directions unconsidered the DCB

a X方向

b Y方向

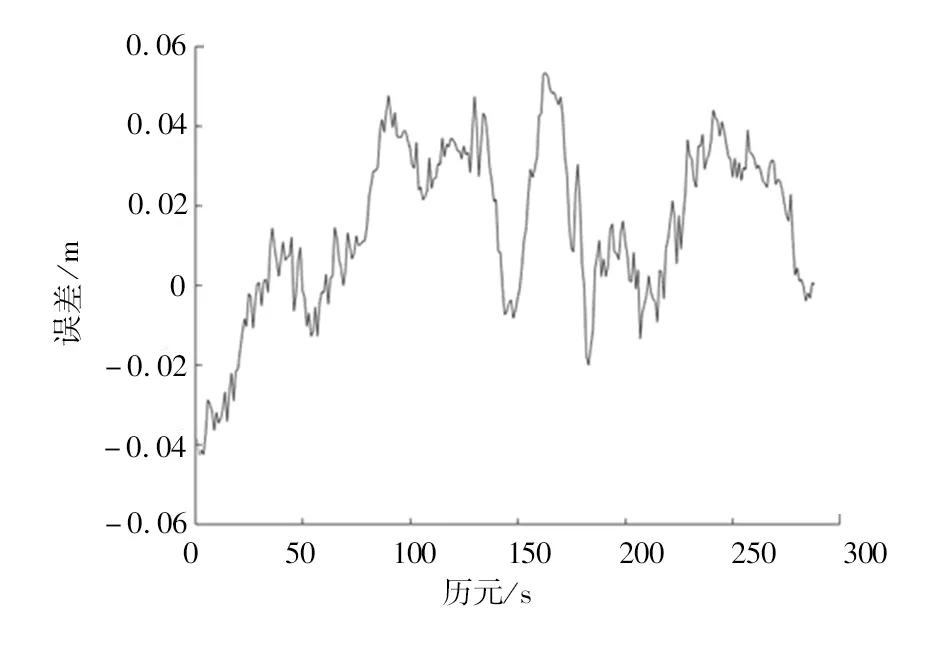
c Z方向图2 考虑DCB的X、Y、Z方向的定位误差变化Fig 2 The variation of the positioning error in the X, Y and Z directions considered the DCB

图1为不考虑DCB影响的情况下，X方向、Y方向、Z方向的定位精度；图2为加入DCB改正文件后，X方向、Y方向、Z方向的定位误差。图1、图2的横坐标均表示历元，纵坐标均表示解算出的坐标与SINEX周解出的坐标间的差值。

从图1、图2可以看出，考虑DCB的影响后，定位精度明显提升。

表1为加入DCB改正文件前后的均方根误差对比。

表1 均方根误差对比Table 1 The comparison of RMS

从表1可以清晰地看出，考虑DCB的影响后，X、Y、Z三个方向的均方根误差均有明显的下降，而且从均值上看，X方向的均方根误差均值从0.023 8 m下降至0.014 1 m，Y方向的均方根误差均值从0.029 1 m下降至0.014 5 m，Z方向的均方根误差均值从0.022 5 m下降至0.004 7 m；从最大值上看，X方向均方根误差的最大值从2.256 9 m下降至0.053 3 m，Y方向均方根误差的最大值从3.442 2 m下降至0.082 9 m，Z方向均方根误差的最大值从2.918 4 m下降至0.057 1 m；从最小值上看，X方向均方根误差的最小值从0.004 1 m下降至0.000 2 m，Y方向均方根误差的最小值从0.005 3 m下降至0.001 0 m，Z方向均方根误差的最小值从0.004 4 m下降至0.000 6 m。显然，考虑DCB的影响后，X、Y、Z三个方向均方根误差最大值与最小值均有明显的下降，定位精度由米降至厘米级别，即考虑DCB的影响后，利用Bernese解算精密单点定位数据时，能获得更高精度的定位结果，定位精度达厘米级。

3 结束语

通过Bernese软件对IGS观测站BFJS站2019年1月1日的观测数据进行了解算，并分是否考虑DCB影响的两种情况进行了实验，结果表明，DCB对精密单点定位的影响表现为系统性误差，对接收机坐标的影响达到几个厘米。因此在高精度的定位中应该认真考虑DCB的影响，必须采用相应的公式进行改正。