开展研究性学习,培养数学建模素养*——以“数列模型在房贷问题上的应用”教学实践为例

广东省梅州市教育局教学研究室(514021) 陈启南 罗 裕

广东省梅县东山中学(514021) 谢婷婷

《普通高中数学课程标准(2017年版)》提出数学学科六大核心素养: 数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析,其中数学建模是对现实问题进行数学抽象,用数学语言表达问题、用数学方法构建模型解决问题的素养.数学建模过程主要包括: 在实际情境中从数学的视角发现问题、提出问题,分析问题、建立模型,确定参数、计算求解,检验结果、改进模型,最终解决实际问题. 如何充分利用高中数学课程,培养数学核心素养? 如何充分利用高中数学课程中相关数学模型,培养学生善于发现和提出问题,用数学模型解决实际问题的意识? 如何设计数学建模研究性学习活动,让学生感悟数学知识与现实世界的紧密联系? 这些问题都是当前中学数学教育工作者热议的话题. 笔者基于对课程标准的理解和认识,在高中数学课堂开展数学建模研究性学习活动,培养学生在现实生活情境中发现和提出问题,利用现有高中知识结构建立和求解模型,在小组研讨分析和同伴互助下解决实际问题. 下面是以“数列模型在房贷问题上的应用”为例,在研究性学习活动中开展数学建模的教学实践和感悟,供各位同仁研讨.

1 立足教材内容,提出研究性学习教学内容

1.1 教材思考应用题,萌发教学实践的想法

在苏教版《普通高中课程标准实验教科书· 数学5(必修)》“2.3.3 等比数列前n项和”章节中,一道关于购房贷款的思考应用题如下:

例1某人2004年初向银行申请个人住房公积金贷款20 万元购买住房,月利率为3.375‰,按复利计算,每月等额还贷一次,并从贷款后的次月初开始还贷. 如果10年还清,那么每月应还贷多少元?

在教学的备课环节,笔者不禁思考,正如例5 所述,在我们现实生活的各方面都蕴涵着数学知识,数学在生活中的应用也处处可见,消费者在购买商品住房时,往往向银行申请购房贷款,采取分期还款的方式来缓解资金的暂缺,消费者该如何选择最优的还款方案? 我们不妨以此题为背景材料,设计研究性问题,组织学生开展基于数学建模的研究性学习活动.

1.2 从数学的视角发现问题,提出研究性问题

为方便学生研究性学习活动的开展,笔者将教材中的例题改编为研究性学习问题如下:

问题1: 张某计划于2020年初向银行申请商业贷款购买住房,请你以小组为单位调查我市各商业银行贷款年利率、贷款期限等相关情况. 目前商业银行主要提供两种购房贷款的还款方式: 等额本息还款和等额本金还款,请你以小组为单位调查这两种还款方式有何不同?

问题2: 若张某向银行申请贷款100 万元购买住房,贷款期限为20年或30年,银行五年以上贷款年利率为4.9%,每月还款一次,张某可以选择等额本息还款或等额本金还款方式,你能否建立不同还款方式的数学模型? 在不考虑其他因素的条件下,他该如何选择哪种贷款期限和还款方式才更为划算? 你能否得出有信服力的一般性结论?

2 立足学生学情,开展研究性学习教学实践

2.11 第一阶段: 学情分析,成立课题研究学习小组

研究性学习参与者是高中学生, 学生知识面已比较广,对生活中的贷款问题有一定程度的了解,具有参与社会调查访谈的能力,已经学习并掌握等差数列和等比数列等相关数学知识,具有初步建立数学模型的能力. 教师遵循互补原则将学生分成若干组,成立课题研究学习小组,在教师指导下各小组选定组长,明确组员彼此分工,根据分工制定学习小组研究计划,规划研究时间,细分研究内容和预定成果等.

2.2 第二阶段: 调查访谈,开展课题研究社会实践

在教师指导下,课题研究学习小组开展对我市各商业银行贷款年利率、贷款期限和还款方式等相关情况的社会调查实践活动. 课题研究学习小组通过网络搜索资源信息、咨询家长与专业人士、走访商业银行采集数据等方式,了解和掌握目前购房贷款不同的还款方式、分期还款的年限、分期付款的方式以及利率等相关情况,调查访谈小组组员填写调查记录表,组长收集每次小组调查反馈的数据和信息.

2.33 第三阶段: 建模活动,引入参数建立数学模型

(1)从数学的视角分析问题.

①等额本息还款: 又称定期付息,贷款人每月按相等的金额偿还贷款本息,其中每月贷款利息按月初剩余贷款本金计算并逐月结清. 即将按揭贷款的本金总额与利息总额相加,将总额平均分摊在还款期限的每个月中,每个月按照固定的金额数目进行还款.

②等额本金还款: 将贷款的本金平均分摊在还款期限的每个月中,同时付清上一交易日至本次还款日之间的利息,随着还款次数的增加,每个月实际支付的还款金额逐月递减.

(2)确定参数建立数学模型.

①理清变量关系,确定模型参数:

设银行贷款本金为m万元,还款期限为n个月,贷款月利率为r. 若采用等额本息还款方式,每月还款金额为a万元,每次还款后剩余贷款本金为mn万元,贷款需支付的总还款额为Sa万元;若采用等额本金还款方式,每月还款金额为bn万元,每月还款利息为Cn万元,贷款需支付的总还款额为Sb万元.

②利用数学方法,构建数学模型:

若采用等额本息还款方式:

数学模型构建思路1: 从还款剩余本金的角度建立数学模型,即计算出逐月还款后所剩本金数额(所剩本金数额=上次剩余本金-当次还款金额中所占的本金部分),还款期限结束时,贷款还清,贷款所剩本金数额为0. 数学模型1 构建过程如下:

第一次还款a后,剩余贷款本金为

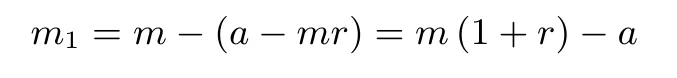
第二次还款a后,剩余贷款本金为

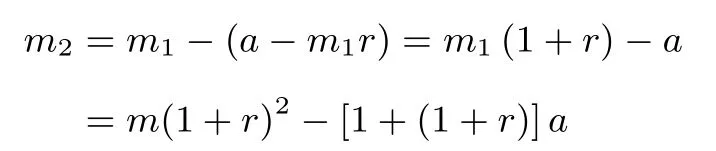
第三次还款a后,剩余贷款本金为

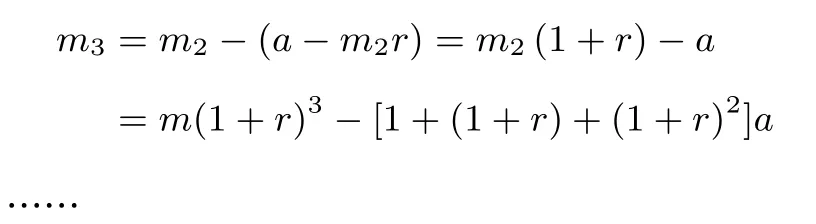
第n次还款a后,剩余贷款本金为

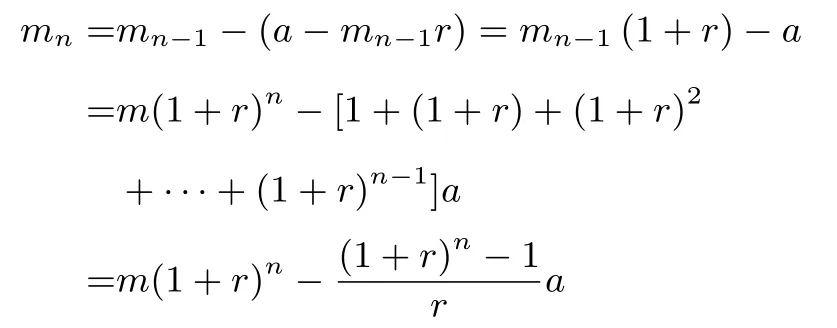
当房贷还清时, 剩余贷款本金mn= 0, 可求每月等额本息还款金额a=;购房需支付的总还款额为Sa=a·n=

若采用等额本金还款方式:

数学模型构建思路2: 从每月还款金额的角度建立数学模型,即计算出每月所需还款金额,其由两部分组成,第一部分是: 贷款的本金平均分摊在还款期限的每个月部分为第二部分是: 付清上一交易日至本次还款日的利息. 数学模型2 构建过程如下:

第二次还款金额为b2=

第三次还款金额为b3==

……

第n次还款金额为

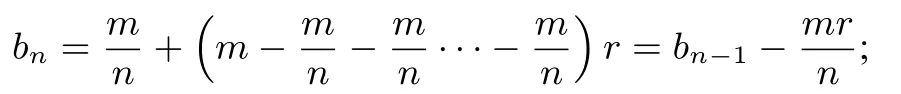
由等差数列定义得: 每月还款金额bn为等差数列,公差为

运用等差数列求和公式, 可求出贷款需支付的总还款额为:

2.4 第四阶段: 检验改进,小组同伴互助改进模型

(1)若采用等额本息还款方式.

数学模型1 检验改进思路: 可考虑从每月还款金额的本利和角度建立数学模型,即每次还款金额及其本利和的总额等于贷款的本金及其本利和的总额(银行贷款本金为m,还款期限结束时,贷款的本金及其利息的总额为m(1+r)n,若每月等额本息还款为a,那么每次还款金额及其本利和的总额等于贷款的本金及其利息的总额). 数学模型1 检验改进过程如下:

第一次还款a, 至还款期限结束时, 其本利和为a(1+r)n-1;

第二次还款a, 至还款期限结束时, 其本利和为a(1+r)n-2;

第三次还款a, 至还款期限结束时, 其本利和为a(1+r)n-3;

……

第n -1 次还款a, 至还款期限结束时, 其本利和为a(1+r);

第n次还款a,其本利和为a.

从而有:a(1+r)n-1+a(1+r)n-2+a(1+r)n-3+···+a(1 +r) +a=m(1 +r)n, 运用等比数列求和公式, 化简a=购房需支付的总还款额为Sa=a·n=

(2)若采用等额本金还款方式.

数学模型2 检验改进思路: 可考虑从每月还款利息的角度建立数学模型,即计算出每月还款利息金额. 由于等额本金还款每个月的本金还款额是固定金额为每月还款利息=上月剩余本金×月利率=总贷款数×[1-(还款月数-1)÷还款次数]×月利率. 贷款需支付的总还款额=各月还款利息总和+贷款的本金. 数学模型2 检验改进过程如下:

第一次还款利息为C1=mr;

第二次还款利息为C2=

第三次还款利息为C3=

……

第n次还款利息为Cn=

由等差数列定义得: 每月还款利息Cn为等差数列,公差为运用等差数列求和公式, 可求出各月还款利息总和为因为贷款需支付的总还款额=各月还款利息总和+贷款的本金,可得Sb=+m=

同理, 每月还款金额bn也为等差数列, 公差为

2.5 第五阶段: 成果汇报,学习小组提交研究成果

(1)利用构建数学模型,计算解决研究性问题.

由研究性学习问题可知,银行贷款本金为100 万元,银行五年以上贷款年利率为4.9%,可求得模型相应参数: 贷款月利率为r= 0.40833%,m= 100,代入上述构建数学模型中:

①当还款期限n=240 时,采用等额本息还款: 购房需支付的总还款额Sa=a·n=≈157.0666(万元) ; 每月还款金额为a=≈0.6544(万元) ; 采用等额本金还款: 购房需支付的总还款额Sb=≈149.2042(万元) ; 每月还款金额为bn=(1+r)(万元)(略).

②当还款期限n=360 时,采用等额本息还款: 购房需支付的总还款额Sa=a·n=≈191.0616(万元) ; 每月还款金额为a=≈0.5307(万元) . 采用等额本金还款: 购房需支付的总还款额Sb=≈173.7042(万元) ; 每月还款金额为bn=(1+r)(万元)(略).

(2)利用构建数学模型,作出最优化支出选择.

通过构建的数学模型计算求解, 若选择贷款期限为20年时, 等额本息还款方式需支付的总还款额为157.0666 万元; 等额本金还款方式需支付的总还款额为149.2042 万元;若选择贷款期限为30年时,等额本息还款方式需支付的总还款额为191.0616 万元;等额本金还款方式需支付的总还款额为173.7042 万元;在不考虑其他因素的条件下,张某可选择贷款期限为20年的等额本金还款方式更为划算.

(3)利用构建数学模型,对比两种方式的优劣.

通过构建的数学模型计算求解,不仅可以解决实际的生活问题,供购房贷款者根据自身家庭的经济实力选择最适合家庭支出的贷款期限和还款方式,而且得出有信服力的结论,供购房贷款者参考依据:

结论①: 贷款期限长短: 贷款期限短,每月还款金额多,支付的总还款额少;贷款期限长,每月还款金额少,支付的总还款额多,不同的贷款期限各有优势,互有利弊.

结论②: 等额本息还款: 每月的还款额相等, 在贷款初期每月的还款中,剔除按月结清的利息后,所还的贷款本金就较少;而在贷款后期因贷款本金不断减少、每月的还款额中贷款利息也不断减少,每月所还的贷款本金就较多. 这种还款方式,实际占用银行贷款的数量更多、占用的时间更长,这种还款方式适合预计收入稳定的人使用.

结论③: 等额本金还款: 每月所还本金固定, 而每月贷款利息随着本金余额的减少而逐月递减,等额本金还款法在贷款初期月还款金额大,此后逐月递减(月递减额=月还本金×月利率). 这种还款方式适合预计收入会逐步减少的人使用.

3 在研究性学习中开展数学建模教学实践感悟

3.1 真实的生活情境是培养数学建模素养的“天然土壤”

数学建模是新课程改革提出的数学学科的核心素养之一,是数学知识应用的重要形式,是联系数学知识与现实世界的重要桥梁, 是应用数学知识解决实际问题的重要途径,课程标准对数学建模素养的不同水平划分提及从实际背景、熟悉情境和综合情境三个层面,发现情境中的数学关系. 因此,教师在开展数学建模活动教学过程中,应发挥“真实的生活情境”是培养数学建模素养的“天然土壤”的作用,从两个视角出发,一是从现实的生活情境中出发,从情境中去发现其蕴藏的数学知识,如: 人口增长问题和投资回报问题中所蕴藏的函数知识,贷款利息问题中所蕴藏的等比数列和等差数列知识等;二是从数学知识出发,寻求数学知识在现实生活情境的应用,如: 解三角形知识在生活中测量问题的应用,三角函数知识在港口水深与货船进港时间问题的应用等;通过两个视角相结合,引导学生深入细致的观察和分析现实生活的情境,培养学生学会用数学的眼光观看世界,用数学的思维思考世界,用数学的语言表达世界.

3.2 多元化学习方式是培养数学建模素养的“发展途径”

数学建模是学生应用数学知识解决现实生活问题的重要途径,学生数学建模素养的形成和发展仅仅靠单一的课堂教学方式难于实现,尤其是在高考指挥棒作用下,虽然教师在数学建模有利于学生能力发展的观点上均有一致共识,但在高中教学任务紧,升学压力大的背景下,数学建模活动的开展往往流于形式,难成规模,不成气候,更缺乏可以参考和借鉴的成熟案例和活动经验. 笔者认为多元化学习方式是培养数学建模素养的“发展途径”,一是立足课堂教学,围绕主题单元教学中应用题专题,开展数学建模教学实践,如: 必修一函数模型及其应用;必修3 算法案例、统计案例;必修4 三角函数的应用等等, 发挥应用题专题教学的生活情境问题,教给学生数学建模的程序和方法. 二是开展研究性学习活动,利用空余时间,让学生打开课堂的栅栏,走进生活,奔向社会,以小组同伴互助的形式开展调查问卷、访谈研究、数据采集,在实际情境中从数学的视角发现问题、提出问题,分析问题、建立模型,确定参数、计算求解,检验结果、改进模型,最终解决实际问题.

3.3 创新意识和科学精神是培养数学建模素养的“成果定位”

教育的核心本质是育人,开展数学建模活动实践,培养学生数学建模素养是实现数学学科“学科育人”的途径,数学建模活动应发挥其独特的学科育人功能,将培养数学建模素养的“成果定位”在创新意识和科学精神上. 数学建模活动搭建了数学与外部世界的桥梁,学生将掌握的数学知识从纸面解题应用于生活实际,将数学方法、数学思想应用于解决生活实际的问题;学生在数学建模活动中,加深了对数学知识、数学方法、数学思想的理解,积累了数学实践和应用的经验,认识了数学知识在解决工程技术、经济发展、社会生活等方面的广泛应用;学生在建模实践中使用数学的语言表达和交流,使用数学的思维创造性解决问题;在同伴互助中学会了交流与合作,激发了学生学习数学、应用数学的兴趣,培养了学生创造性解决问题的能力,增强了学生的创新意识和科学精神.