右端不连续奇异摄动问题的空间对照结构

倪明康潘亚飞吴 潇

(1.华东师范大学数学科学学院,上海200062;2.上海市核心数学与实践重点实验室,上海200062;3.南京工程学院数理部,南京211167)

许多生物、化学、工程和物理现象可由带边值问题的微分方程或者方程组来描述.每当将面临的问题转化为数学模型时,学者们总是想抓住重要的量而舍弃可以忽略的量,其中就包括小参数.包含小参数的模型称为摄动模型,而不包含小参数的简化模型称为非摄动或者退化模型.在研究中,摄动模型解可以由不带小参数的退化部分替代,前提是退化问题的解必须与对应的摄动问题的解充分接近.这种做法在正则摄动问题中是可行的,但是在奇异摄动问题中是不成立的.

奇异摄动问题出现在应用数学的许多分支中,如流体力学中的边界层、固体力学中的边缘层、量子力学中的转点以及数学中的Stoks线和面.小参数扰动会使相关的变量在非常狭窄的区间内快速变化.在这些问题中,小参数的扰动会使相关的变量在区域边界或内部某点附近极小的领域内快速变化.

近1个世纪以来,奇异摄动问题的研究得到了蓬勃的发展[1-26],各种奇异摄动方法得到了不断发展[27-39].同时,我国许多著名学者为奇异摄动理论的发展也作出了卓越的贡献[40-60],如对于连续的快慢系统,Tikhonov定理[26]的经典结果是,在满足一系列确定条件时(特别是稳定性条件≤-κ,κ＞0),(z(t),y(t))是如下方程的解:

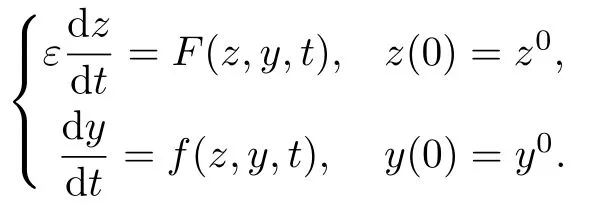
当ε→0时,在任何有限区间[0,T0](T0＜T)上,(z(t),y(t))是一致收敛于函数对,且满足.这里,函数z=φ(y,t)是方程F(z,y,t)=0的根,而函数是如下方程的解:

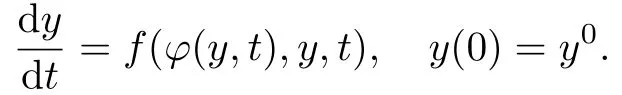
进一步,函数y(t)在区间[0,T]上一致收敛于.这样,无论快慢变量都是收敛的,并且对快变量一致收敛性是在初始点任意邻域之外.

近年来,大量的工作是研究奇异摄动问题中的内部层现象,这类解习惯称之为空间对照结构.产生这种结构的一个原因是微分系统的不连续性.不连续奇异摄动系统是指向量场不连续的奇异摄动系统,在实际力学和应用科学等领域中广泛存在,如碰撞减振器、疾病传播、市场经济模型、刹车系统等.不连续微分系统一直得到广泛研究[61-64].最近,Shi等[65]结合动力系统的分支理论讨论了分段光滑微分系统最大极限环个数问题;Liang等[66]研究了除鞍-鞍型以外的平面分段线性折射系统的极限环问题;Kadalbajoo等[67-69]概述了1908～2009年利用渐近方法和数值方法研究这类奇异摄动问题近似解的发展情况.对于因不连续性而产生内部层的奇异摄动问题的研究,主要始于1970年,因此Sharma等[70]论述了众多学者在1970～2011年对这类奇异摄动问题的研究.不连续奇异摄动问题在过去一百年间有巨大的发展,很难用一篇综述介绍所有类型的问题.特别地,右端不连续的奇异摄动问题十分有挑战性,对其研究还刚刚起步,仅停留在退化问题只有单根的奇异摄动系统，以及Tikhonov系统.事实上,在自然科学研究的各个领域中,当处理带有小参数的奇异摄动问题时常常碰到方程右端是不连续的奇异摄动动力系统.如在机械工程中,由于碰撞和摩擦这些不连续因素使得齿轮传动系统构成不连续系统,脑功能模型所反映的神经元的不连续传递规律以及解释由不同介质组成的超导体所产生的内部层现象等.因此,本综述将详细介绍近5年来本课题组在这一领域的工作.

1 右端不连续的二阶非线性奇摄动问题

2015年,Ni等[71]和Levashova等[72]分析了具有不连续反应项的奇摄动反应扩散方程[13,73-74]的稳态情形,并将渐近方法推广到具有不连续项的问题.对右端不连续的二阶常微分方程的讨论由此展开.

1.1 右端不连续二阶半线性方程

考虑如下奇异摄动边值问题:

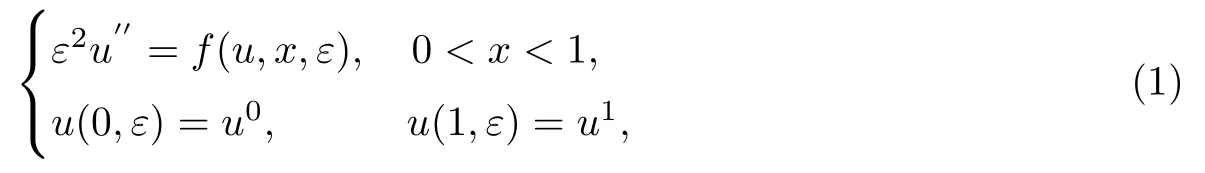
式中:ε∈Iε0={ε|0＜ε＜ε0≪1}是小参数.设x0为区间(0,1)上的给定常数,

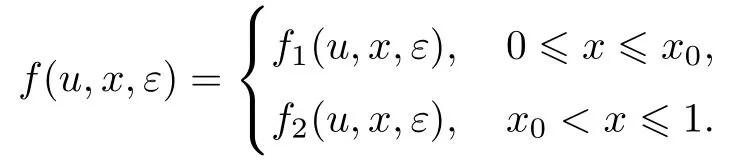
易见,问题(1)的解u(x,ε)满足u(x,ε)∈C1[0,1]∩(C2(0,x0)∪C2(x0,1)).

假设如下条件成立.

条件1假设函数f1(u,x,ε)和f2(u,x,ε)是分别定义在区域Iu×[0,x0]×Iε0和Iu×[x0,1]×Iε0上的充分光滑函数,其中Iu为函数u(x)允许的取值范围,并且在x=x0点满足

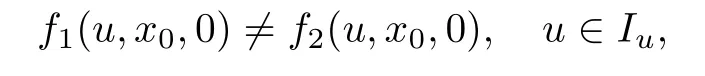
即函数f(u,x,ε)在点x=x0处间断.

条件2假设退化方程f(,x,0)=f1,2(,x,0)=0分别有孤立的退化解(x)=φ1(x),0≤x≤x0和(x)=φ2(x),x0≤x≤1,且满足φ1(x0)̸=φ2(x0).为了不失一般性,不妨假设φ1(x0)＜φ2(x0).

条件3假设函数f(u,x,0)满足如下条件:

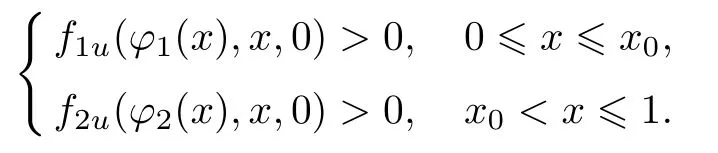
考虑如下辅助系统:

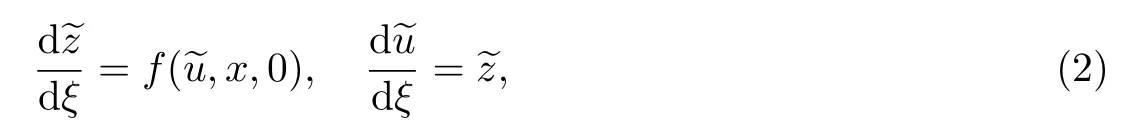
式中:x为参数.由条件2和3可知,对每个固定的x,点(φi(x),0),i=1,2是问题(2)的鞍点型平衡点.

为了确定在端点x=0和x=1邻域内的边界层函数的首项,考虑如下的辅助系统:

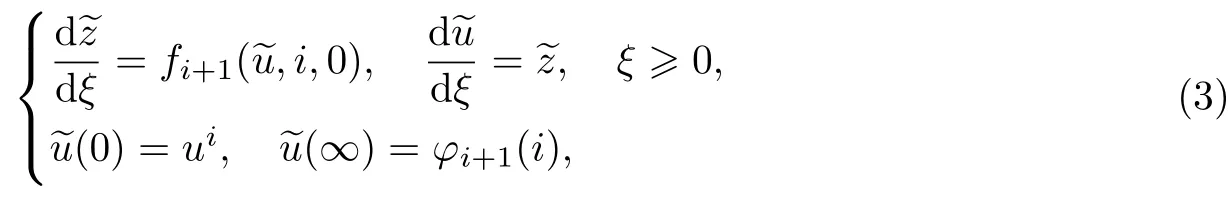
式中:i=0,1,并且满足

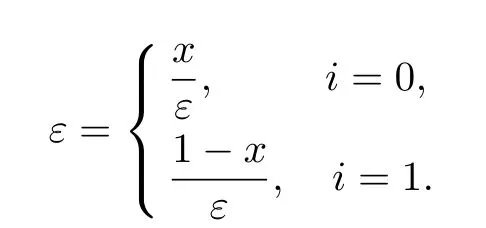
为了明确起见，不妨假设φi+1(i)＞ui.由条件2和3可得,在相平面上存在如下形式的分界轨道:

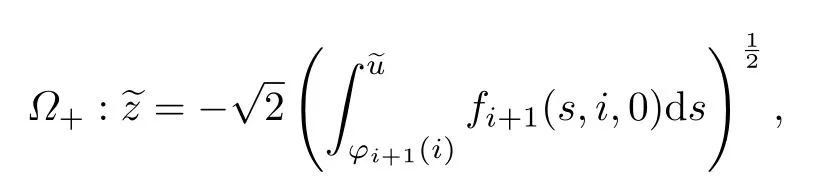
并且当ξ→+∞时,分界轨道趋近平衡点(φi(i),0),i=0,1.因此,问题(3)的可解性条件为边值落在退化方程相应根的吸引域中.

条件4假设在相平面中,垂线=ui,i=0,1,与分界轨道Ω+横截相交,等价于对任意的∈(φi+1(i),ui]有fi+1(s,i,0)ds＞0.

为了确定内部层首项,考察当参数x=x0时,辅助系统(2)的如下形式的边值问题:

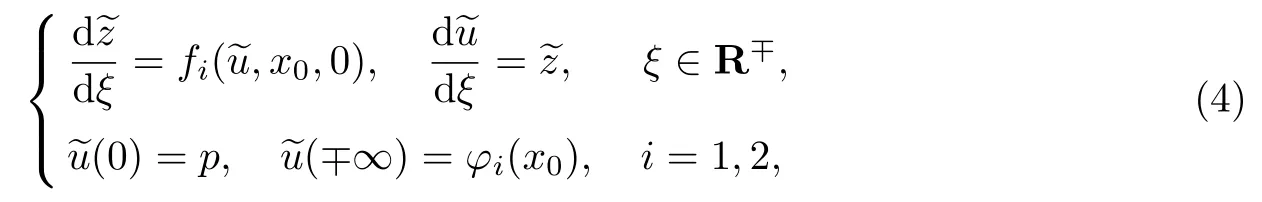
式中:ξ=(x-x0)/ε;p∈(φ1(x0),φ2(x0)).由条件2和3可得,在相平面上存在的分界轨道为

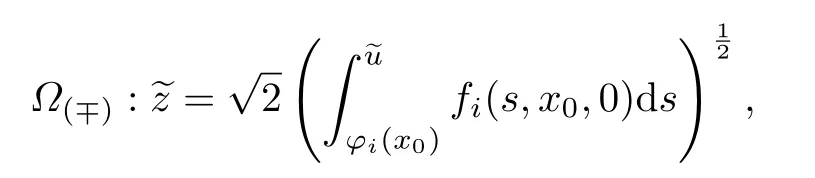
并且当ξ→∓∞时,分界轨道趋近平衡点(φi(x0),0),i=1,2.因此,问题(4)的可解性条件为=p在退化方程相应根的吸引域中.

条件5假设在相平面(~u,~z)中,对任意的p∈(φ1(x0),φ2(x0)),垂线=p与分界轨道Ω(∓)相交,等价于

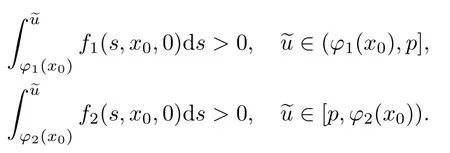
记

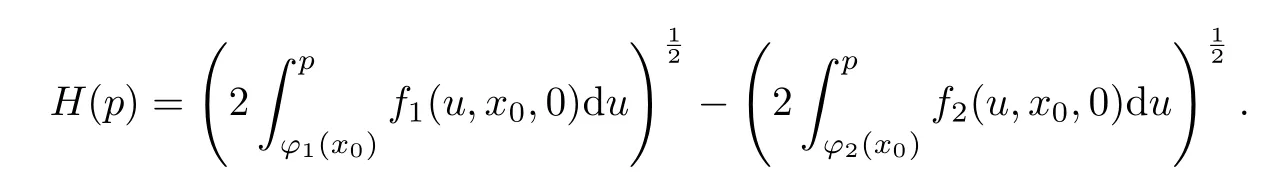
条件6假设方程H(p)=0有唯一解p=p0.

方程H(p)=0可化简为如下形式:

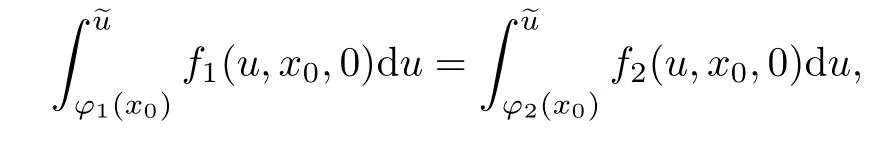
并且

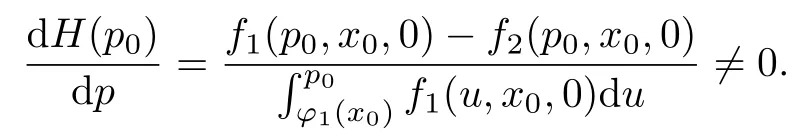
为了构造问题(1)解的渐近展开式,分别考虑2个边值问题,即区间[0,x0]上的边值问题和区间[x0,1]上的边值问题:

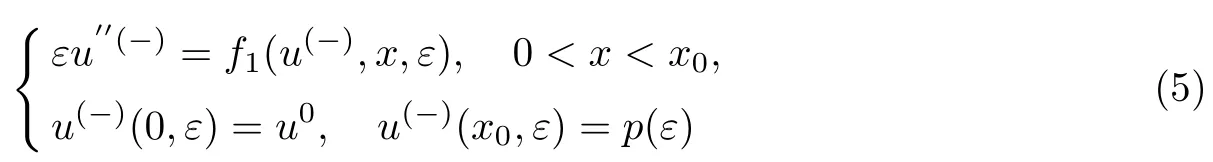
和

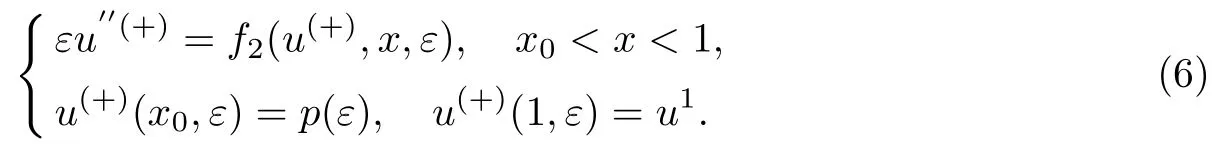
在问题(5)和(6)中,函数p(ε)待定,有如下形式的渐近展开式:

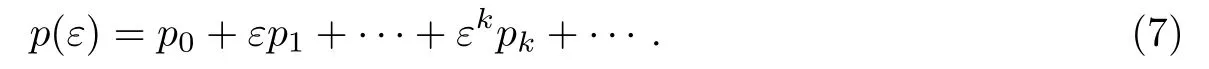
当x∈[0,x0]时,问题(5)解的渐近展开式为

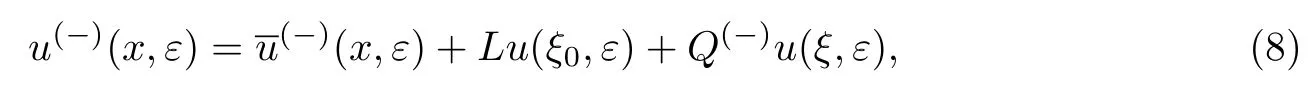
式中:

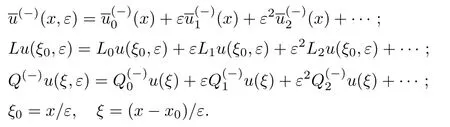
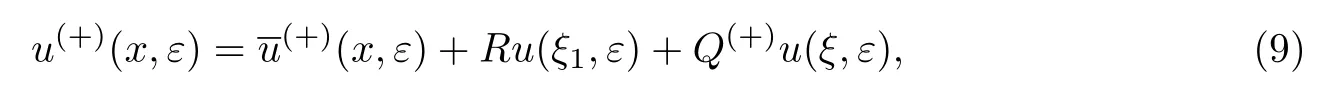
用边界层函数法的标准方法构造渐近解.首先,将问题(8)和(9)分别代入问题(5)和(6);然后,依照不同尺度x,ξ,ξ0和ξ1分离变量;最后,比较ε同次幂系数可以得到确定展开式中各项系数的方程.特别地,正则部分首项满足退化方程.当k＞0时,满足如下代数方程:

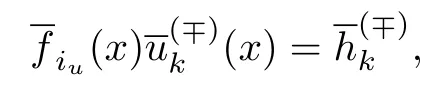
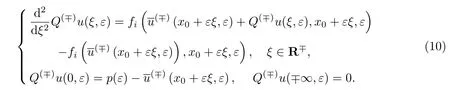
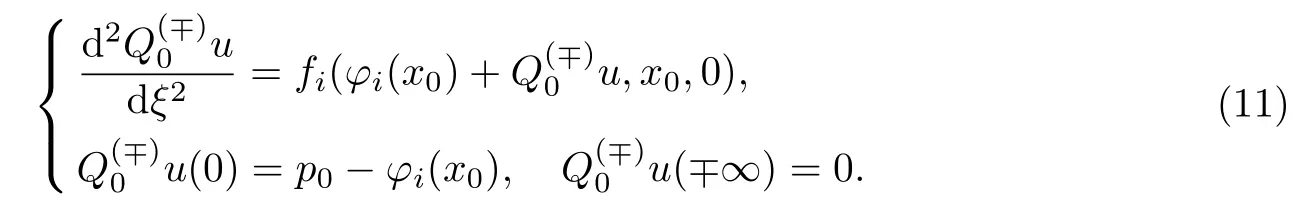
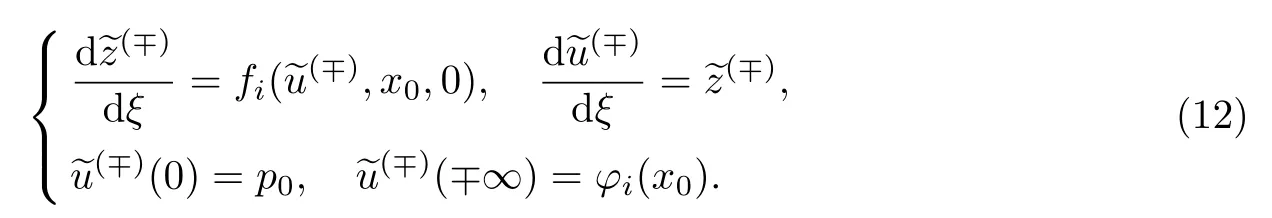
问题(12)是一阶可分离变量微分方程,等价于辅助系统.由条件2,3和5可得解,且由条件2可得解具有指数衰减性:

式中:c和κ是与ε无关的正常数.

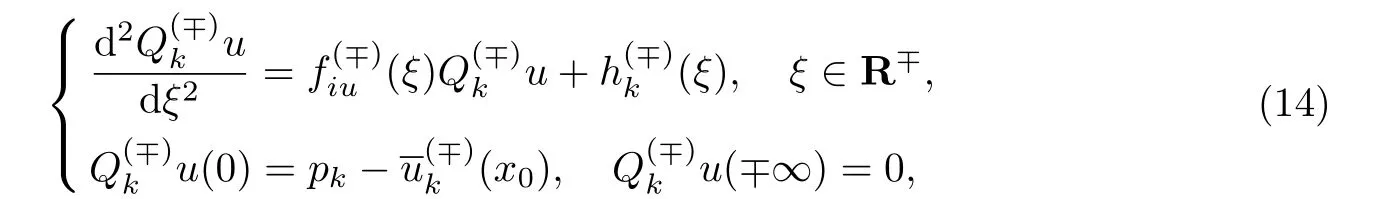
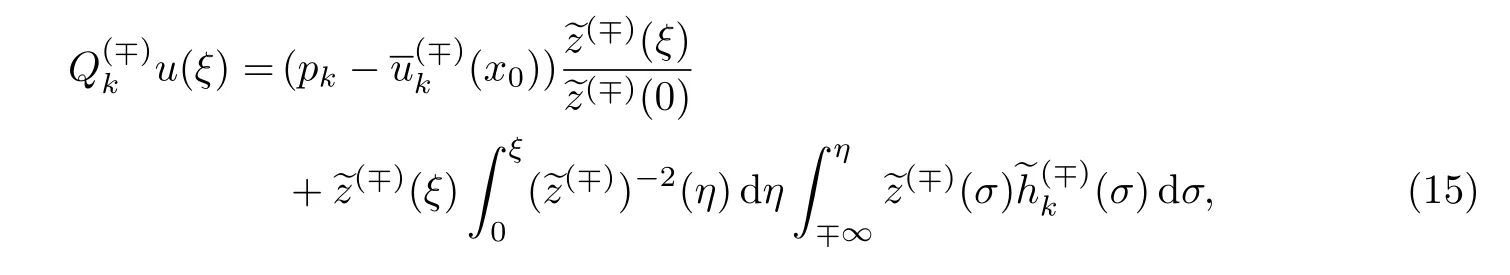
满足类似(13)的指数衰减.

注意最终的解函数中包含待定量pk,k≥0,可由如下光滑缝接条件确定:

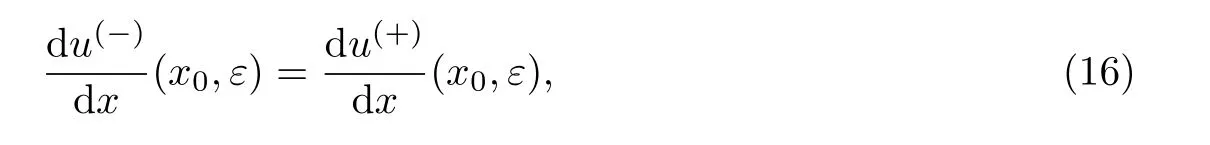
即问题(5)和(6)解的导函数在间断点x0处相等.

等式(16)两边按ε整数次幂展开,并且比较展开式两边ε的各阶系数可得

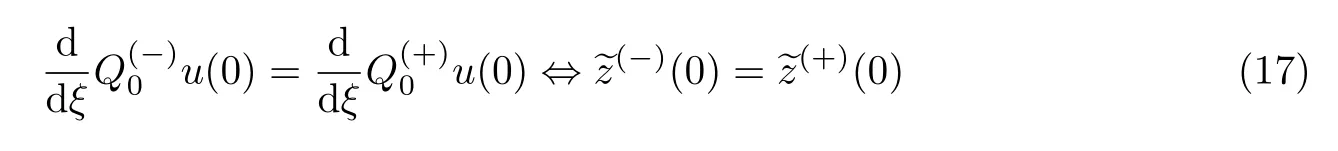
和

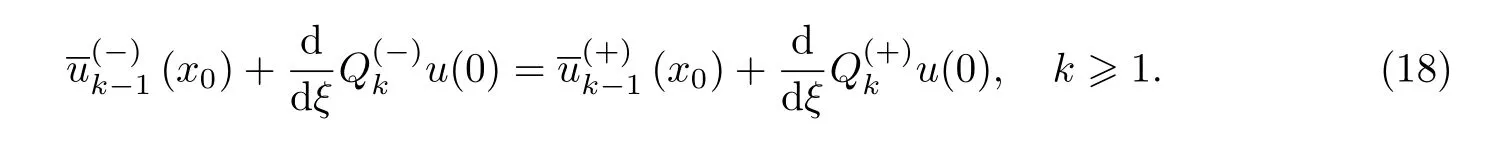
这一系列方程可确定展开式(7)的各项系数.

首先确定p0.在标准算法下,由式(11)可得

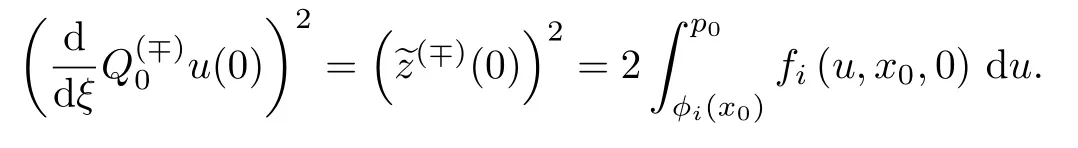
因此,由缝接条件(17)可知,p0由条件6确定.

将方程(14)代入缝接条件(18),将得到如下确定pk(k≥1)的方程:

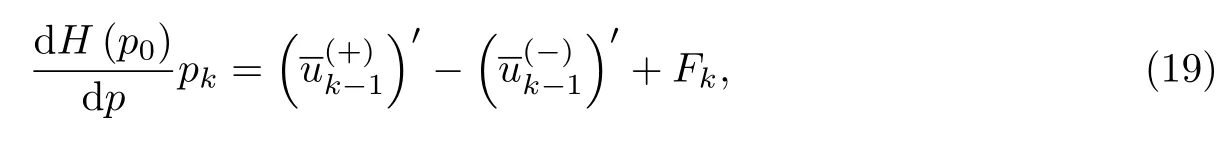
式中:

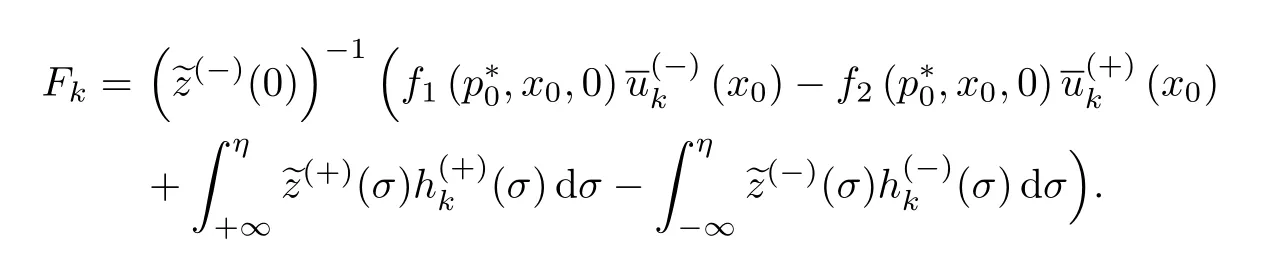
至此,对任意k≥0已确定内部层级数系数函数.因此,可得问题(1)解的n+1阶渐近展开式

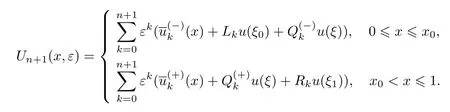
将上面的讨论最终归结为如下定理.

定理1如果满足条件1～6,那么问题(1)的解u(x,ε)存在,且满足

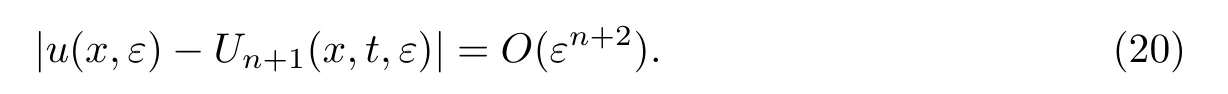
1.2 右端不连续二阶拟线性方程

Ni等[75]主要研究了二阶拟线性方程Dirichlet问题

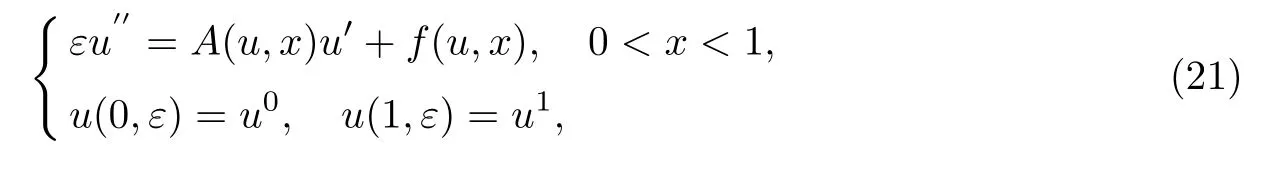
式中:ε＞0是小参数.设x0为区间(0,1)上给定常数,函数A(u,x)和f(u,x)为

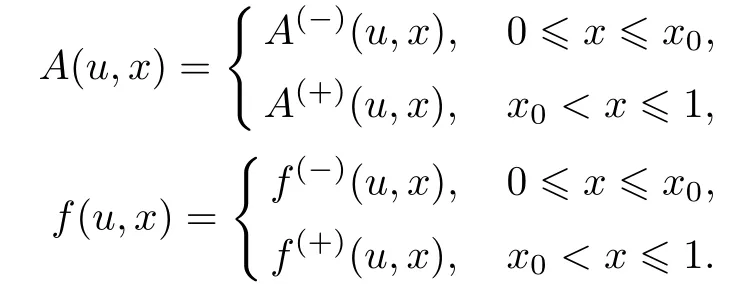
类似地,问题(21)的解u(x,ε)也满足u(x,ε)∈C1[0,1]∩(C2(0,x0)∪C2(x0,1)).

假设如下条件成立.

条件7假设函数A(∓)(u,x)和f(∓)(u,x)为分别定义在区域Iu×[0,x0]和Iu×[x0,1]上的光滑函数,其中Iu为函数u(x)允许的取值范围,且在x=x0处满足

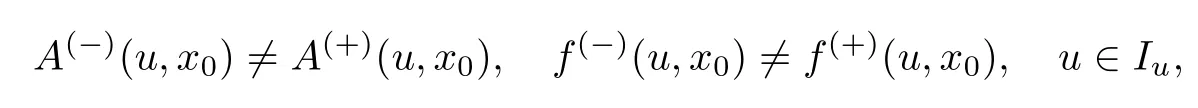
即函数A(u,x)和f(u,x)在x=x0处间断.

条件8假设退化系统

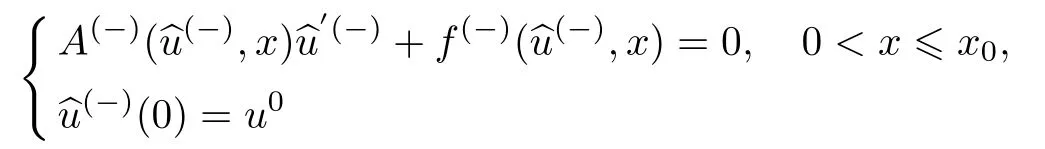
和

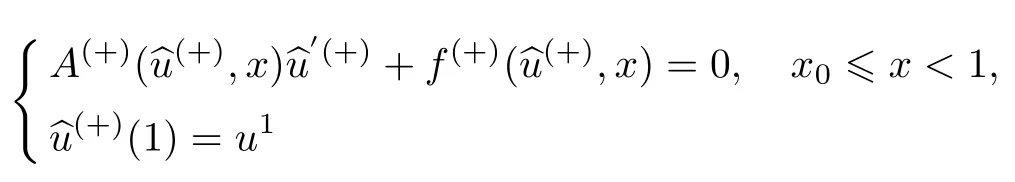
有唯一退化解φ1(x),0≤x≤x0和φ2(x),x0≤x≤1,并且退化解满足φ1(x0)̸=φ2(x0).为了不失一般性,不妨假设φ1(x0)＜φ2(x0).

条件9假设函数A(−)(u,x)和A(+)(u,x)满足不等式

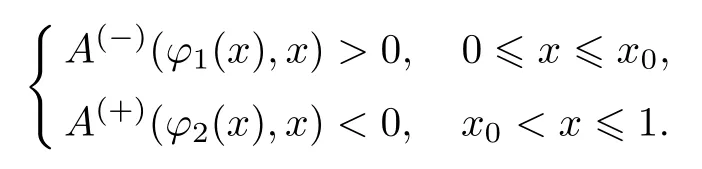
条件9意味着问题(21)在点x=x0附近有内部层.

为了找到内部层首项,引入辅助变量z=du/dx,并假设之后将确定.可得辅助系统

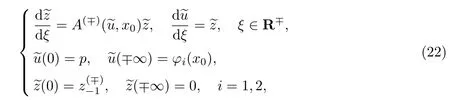
式中:ξ=(x-x0)/ε;p∈(φ1(x0),φ2(x0)).由条件8和9,可得在相平面(~u,~z)上存在分界轨道,可显式表示为

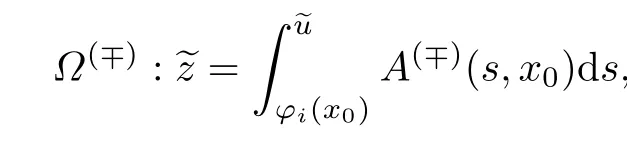
并且当ξ→∓∞时,分界轨道进入平衡点(φi(x0),0),i=1,2.问题(22)的可解性条件为=p在退化方程相应根的吸引域中(见条件10).

条件10在相平面中,对任意的p∈(φ1(x0),φ2(x0)),垂线=p与分界轨道Ω(∓)相交,即

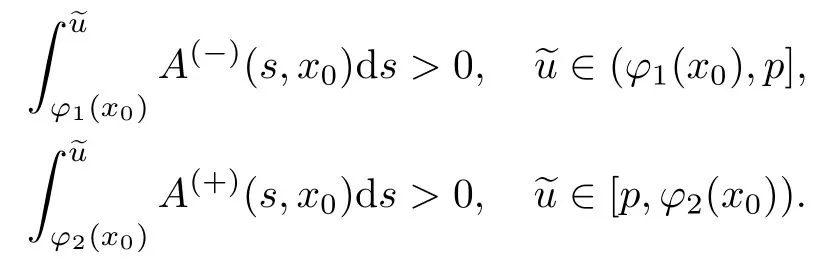
类似地,运用边界层函数法构造问题(21)的渐近解,其中渐近解的展开式与式(8)相似.但值得注意的是,不同于半线性问题,由于退化问题的解满足边界条件,故拟线性问题的解在端点处没有边界层,仅在间断点x0附近有内部层.同时需要注意辅助变量z(x0,ε)的展开式从ε−1开始.

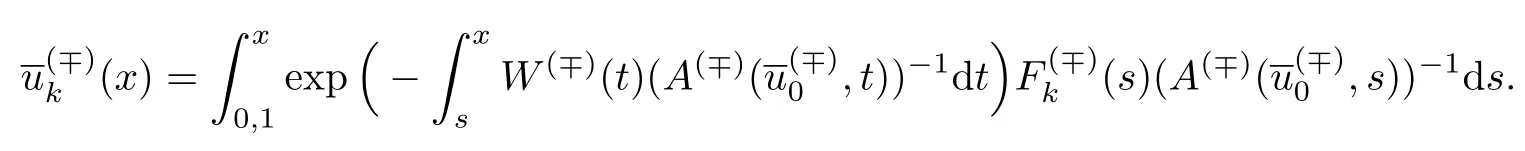
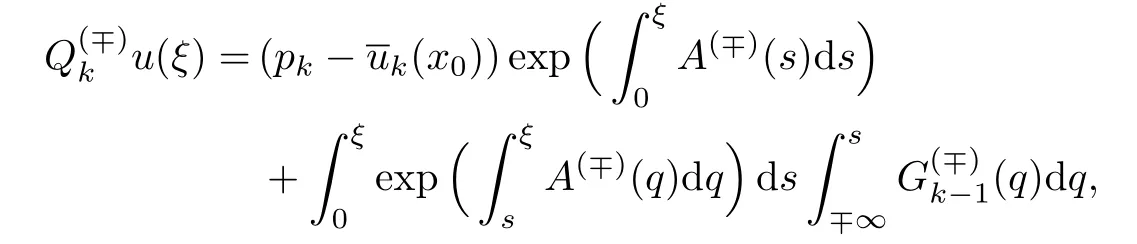
式中:pk为待定量,k≥0,可由光滑缝接条件(16)确定.由于u′=z,可得等价条件

首先,确定p0.比较展开式两边ε−1系数,可得.记

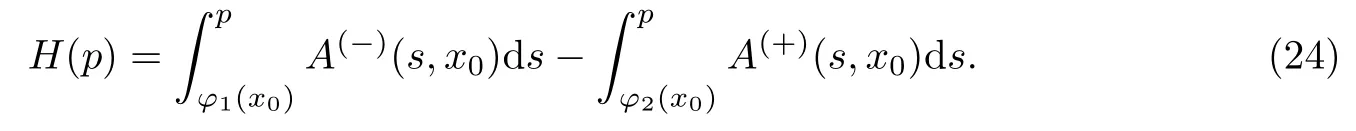
接下来证明H(p)有唯一解p0∈(φ1(x0),φ2(x0)).由问题(24)可得

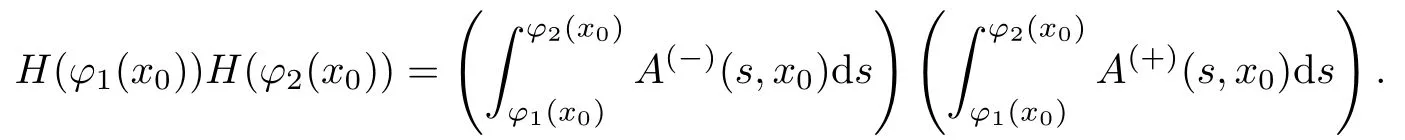
结合条件9中不等式,可得

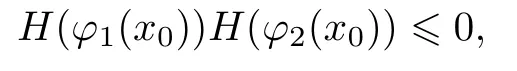
说明一定存在p0∈(φ1(x0),φ2(x0)),使得H(p0)=0.又由条件9,有H′(p)=A(−)(p,x0)-A(+)(p,x0)＞0,由此可得p0的唯一性.

接下来确定pk.当k≥1时,缝接条件可写为

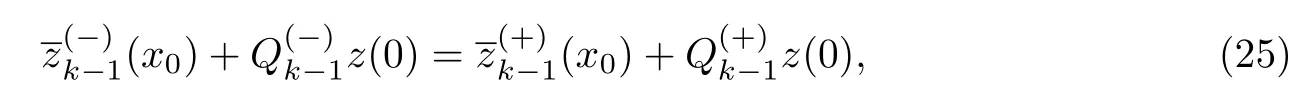
可得

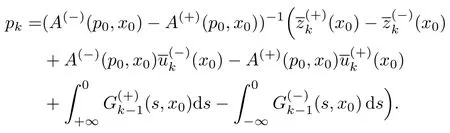
因此,可得问题(21)的解u(x,ε)的n+1阶渐近展开式

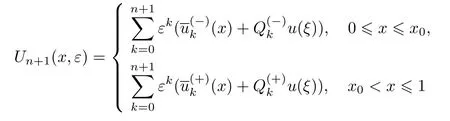
和如下定理.

定理2如果满足条件7～10,那么,对充分小的ε＞0,问题(21)的解u(x,ε)存在且满足

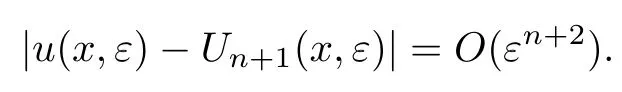
1.3 右端不连续二阶弱非线性方程

Pan等[76]主要考虑二阶弱非线性方程Dirichlet问题

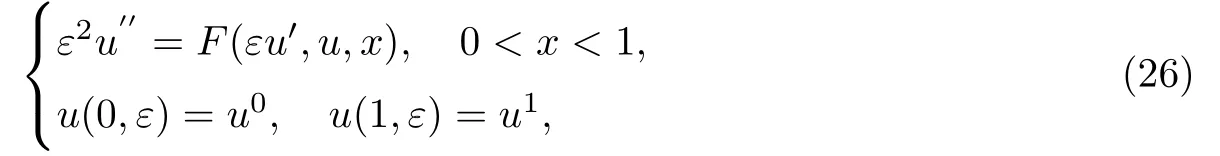
式中:ε＞0为小参数.设x0为区间(0,1)上给定常数,F(εu′,u,x)的表达式为

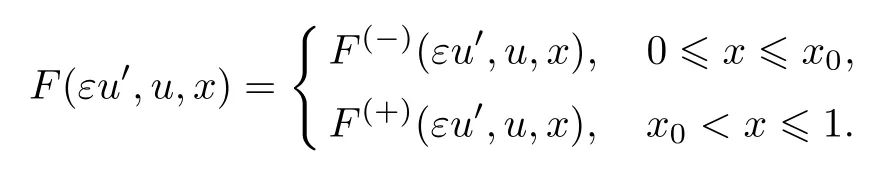
记z=εu′,Iz和Iu为包含原点的有界开区间,定义

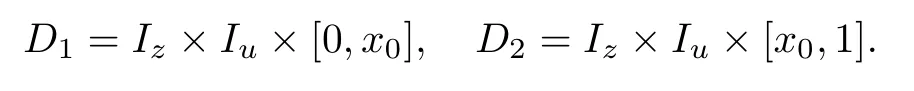
假设如下条件成立.

条件11假设,且满足不等式

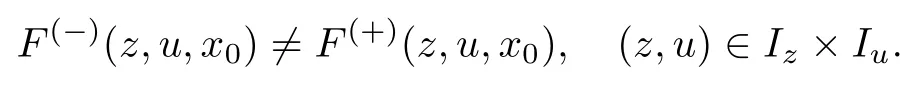
条件12假设退化方程有孤立的退化解φ1(x)(0≤x≤x0)和=φ2(x)(x0≤x≤1),且满足φ1(x0)̸=φ2(x0).为了不失一般性,不妨假设φ1(x0)＜φ2(x0).

条件13假设函数F(u,x,0)满足如下条件:

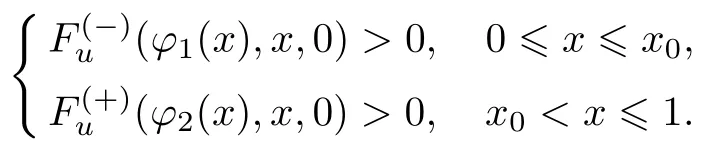
考虑辅助系统

由条件12和13可知,特征方程

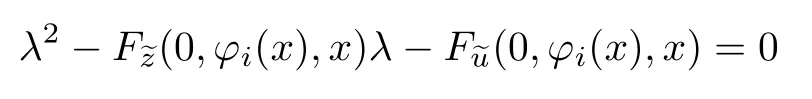
满足

及

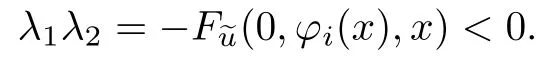
为了确定边界层函数首项,在系统(27)中分别令x=0和x=1,可得如下边界层问题:

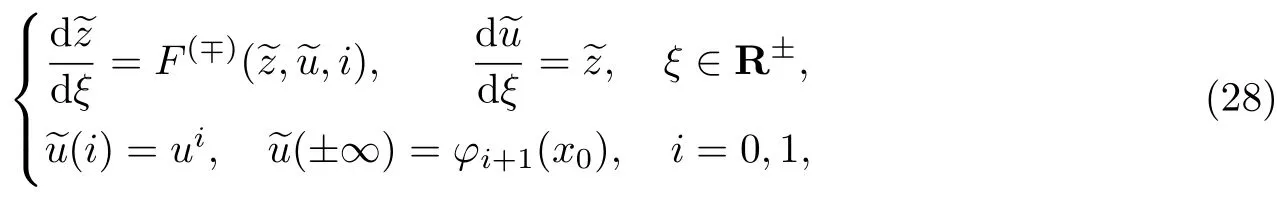
式中,

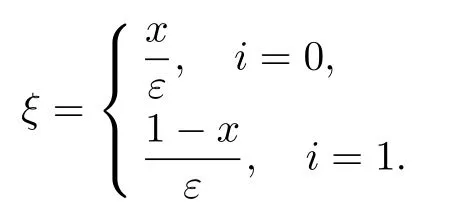
由条件12和13可得,在相平面(~u,~z)中存在分界轨道满足当ξ→±∞时进入平衡点(φi+1(x0),0).问题(28)的可解性条件为边值落在退化方程相应根的吸引域中,即有如下条件成立.

条件14假设在相平面上,垂线与分界轨道相交.

为了找到形式渐近解内部层首项,在系统(27)中令x=x0,可得

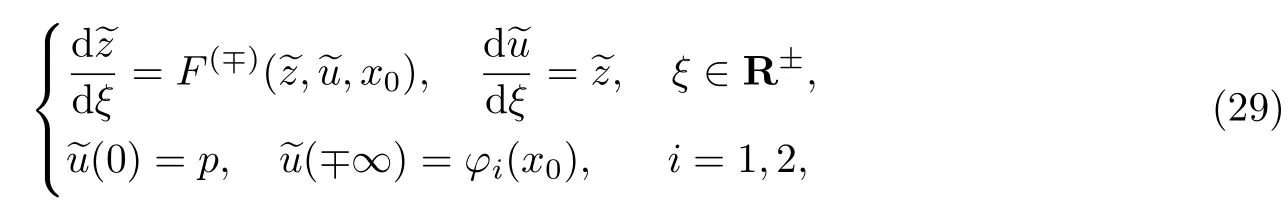
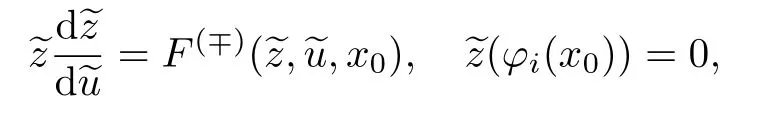
并且,当ξ→∓∞时,分界轨道趋近平衡点(φi(x0),0),i=1,2.特别地,在某些情况下我们可以写出分界轨道的显式表达式,如当F的表达式为

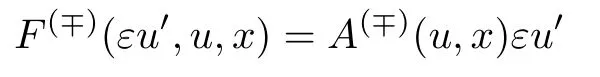
时,分界轨道可表示为

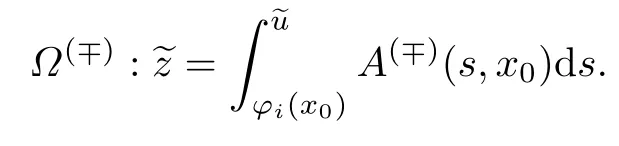
问题(29)的可解性条件与条件14类似.因此假设如下条件成立.

条件15假设在相平面上,对任意p∈(φ1(x0),φ2(x0))垂线=p与分界轨道相交.

条件16假设方程H(p)=0有唯一解p=p0,其中p0∈(φ1(x0),φ2(x0)).这个条件说明.

这里构造问题(26)的解u(x,ε)的渐近展开式,满足在x=x0附近存在内部层,在x=0和x=1附近存在边界层.因此,运用边界层函数法,类似1.1节构造过程,可以得到问题(26)的解u(x,ε)的n+1阶渐近展开式

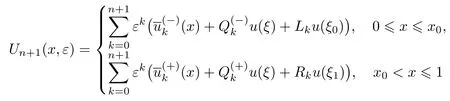
和如下定理.

定理3如果满足条件11～16,那么对充分小的ε＞0,问题(26)的解u(x,ε)存在,并且满足

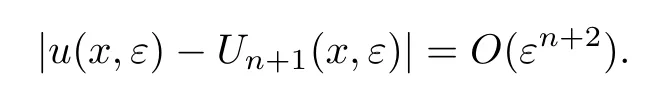
2 右端不连续的常微分方程组

考虑常微分方程组的齐次Neumann问题[77]

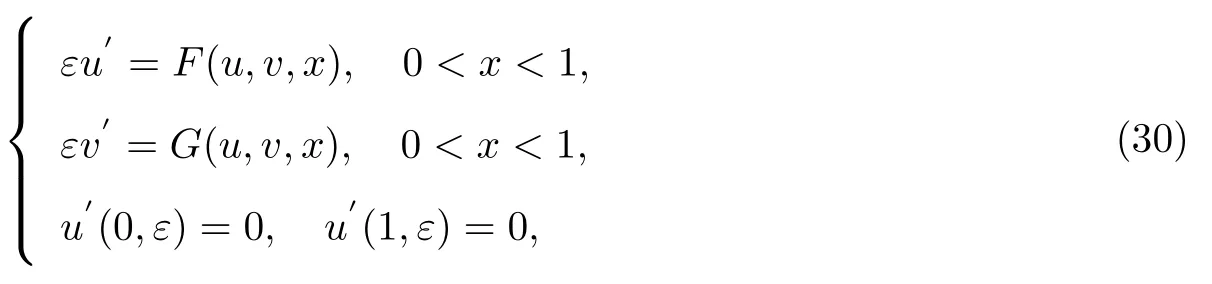
式中:ε＞0为小参数.设x0为区间(0,1)上给定的常数,函数F(u,v,x)和G(u,v,x)为

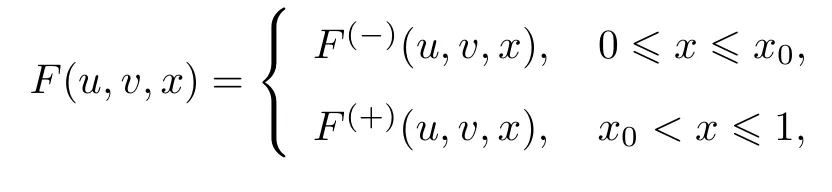
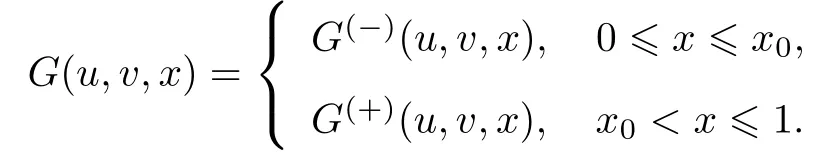
首先定义D1=Iu×Iv×[0,x0],D2=Iu×Iv×[x0,1],其中Iu和Iv为未知函数u和v的取值区间.假设如下条件成立.

条件17假设,而且

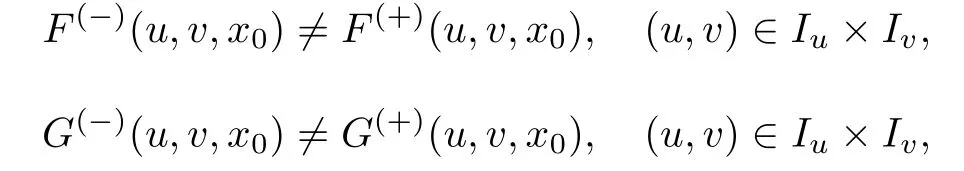
即函数F(u,v,x)和G(u,v,x)在点x=x0处间断.

接下来要构造的是问题(30)的多尺度一致有效渐近解(u(x,ξ),v(x,ξ)),在x=x0附近包含内部层.因此,应分别考虑退化系统和辅助系统.

条件18退化方程F(u,v,x)=0,G(u,v,x)=0在区间[0,1]上有不连续的孤立解,即

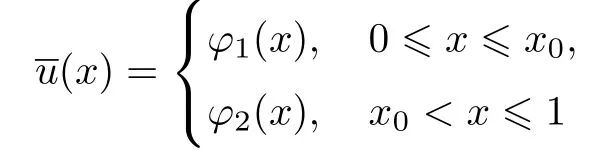
和

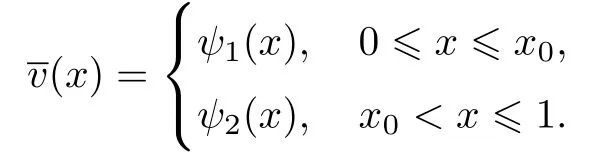
不妨假设(φi(x),ψi(x)),i=1,2充分光滑,且满足φ1(x0)＜φ2(x0).

这里光滑性条件依赖于所构建的解的渐近展开式的阶数,而将要讨论的是任意阶渐近展开式,因此不妨假设所涉及的函数除F和G外都是无穷阶可微.考虑辅助系统

式中:x为参数.

条件19假设

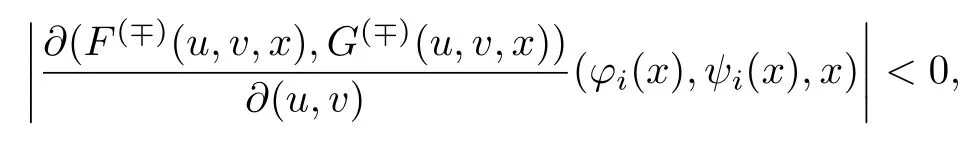
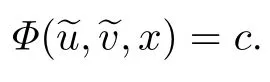
为了得到渐近展开式内部层的首项,令系统(31)中x=x0,得

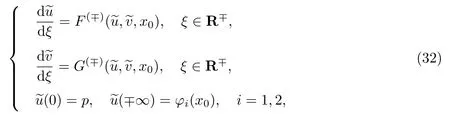
由条件18和19,在相平面(~u,~v)中存在分界轨道.进一步,假设分界轨道为

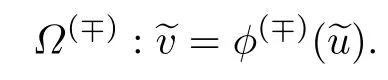
当ξ→∓∞时,分界轨道趋近平衡点Mi,i=1,2.问题(32)的可解性条件为=p,在退化方程相应根的吸引域中,可表达为如下条件.

条件20假设在相平面(~u,~v)中,对任意p∈(φ1(x0),φ2(x0))垂线=p与分界轨道Ω(∓)相交.

记H(p)=ψ1(x0)+ϕ(−)(p-φ1(x0))-ψ2(x0)-ϕ(+)(p-φ2(x0)).

条件21假设方程H(p)=0有解p=p0,其中p0∈(φ1(x0),φ2(x0)),而且.

注意到这里为了专注讨论二维方程组内层问题,本课题组给出的是关于变量u的齐次Neumann条件,这使得边界层首项(主项)为0,因此构造形式渐近解时直接略去了边界层.当然可以提其他类型边界条件,如混合边界条件等,只是在构造近似解时要调整相应边界层;另一方面,要注意当给出的是关于变量u的定解条件时,为了得到一阶微分方程组连续的解,缝接条件为变量v在间断点x0处连续,即v(x0-0)=v(x0+0).

仍然用标准边界层函数法求近似解.高维微分方程组特别的地方是对内部层级数高阶系数函数的求法.

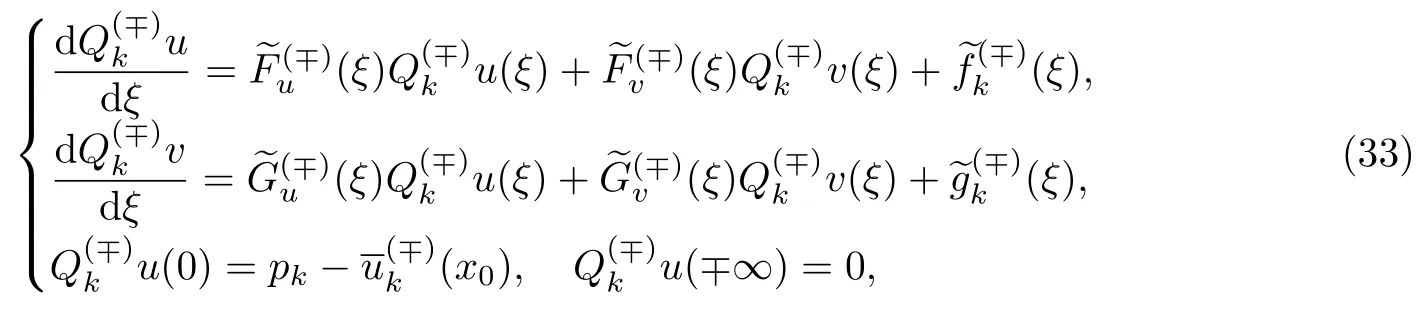
接下来用叠加原理求解非齐次系统(33).考虑如下2个系统:

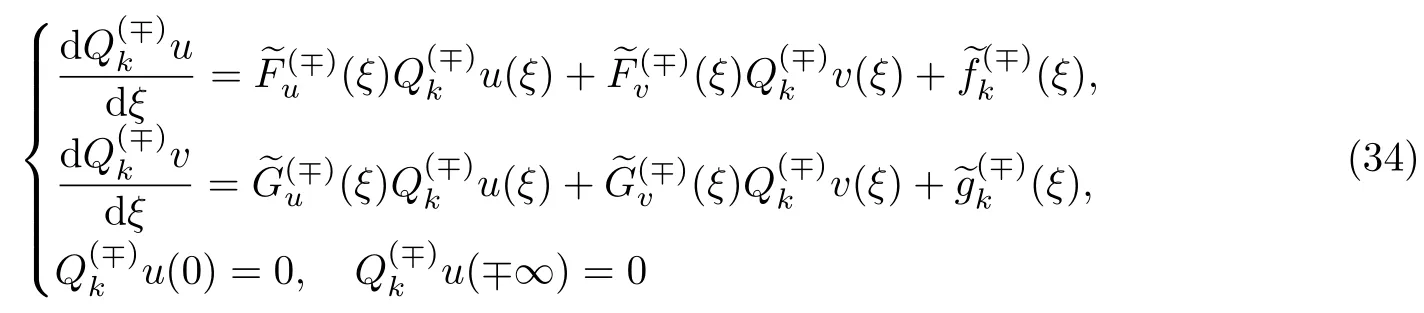
和

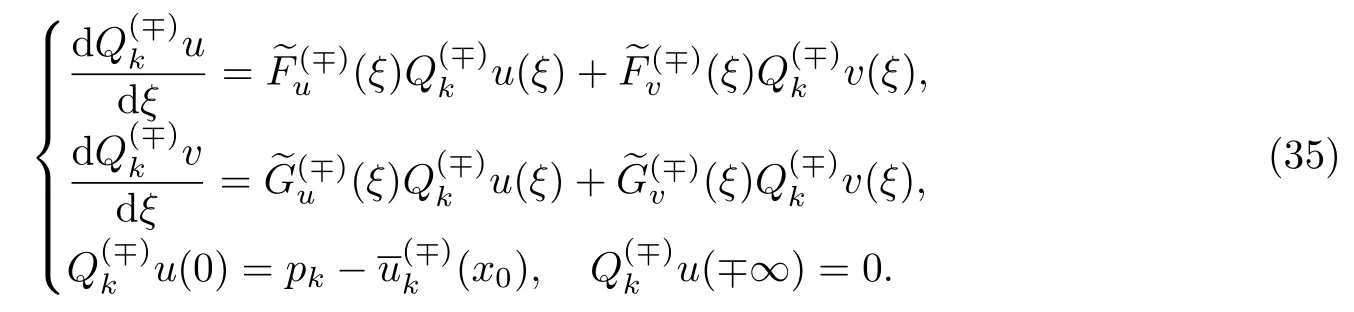
为了找到方程(34)的一个特解,令

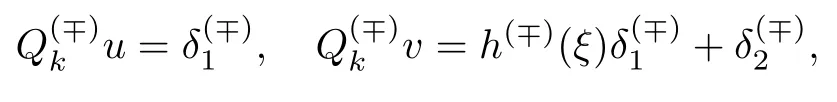
然后将其代入方程(34),可得

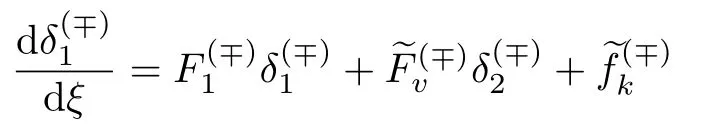
和

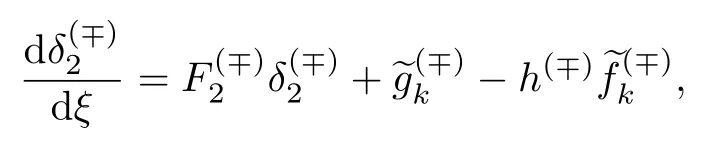
式中:

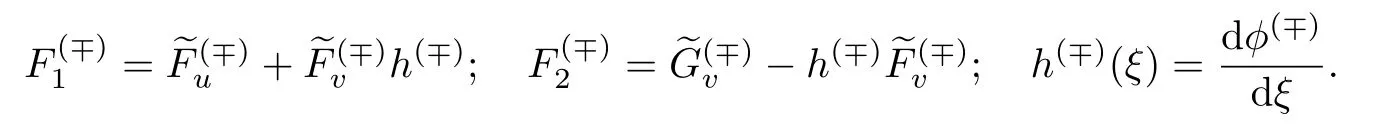
解得

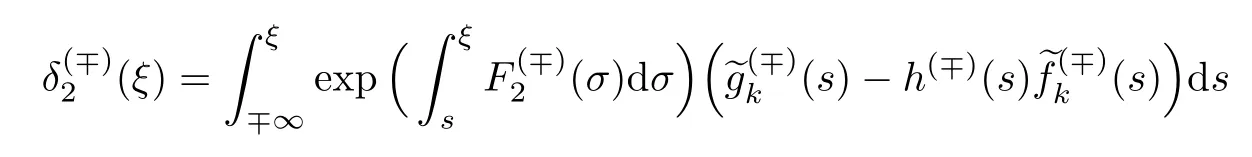
和

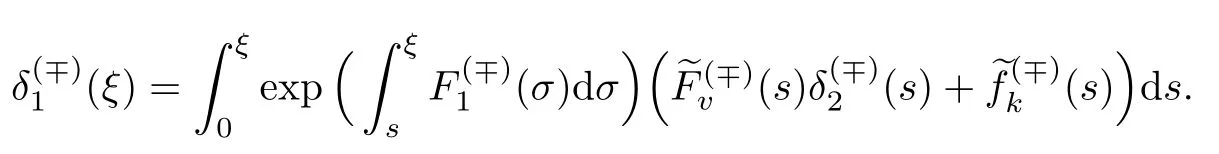
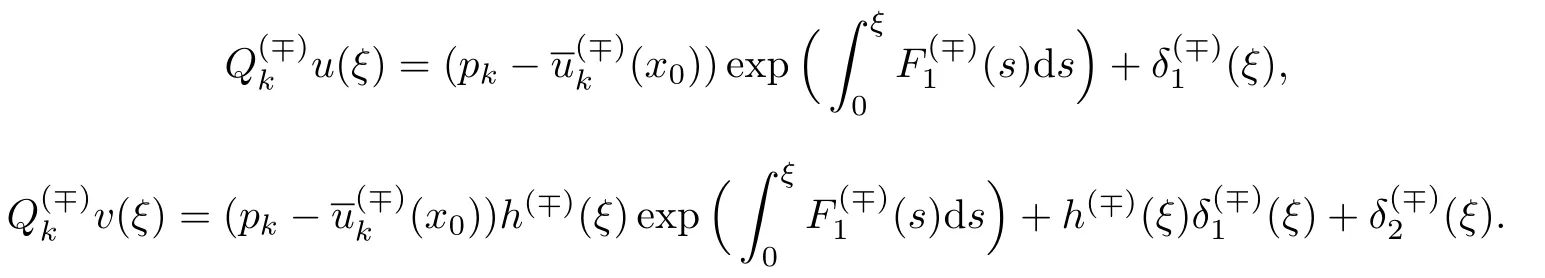
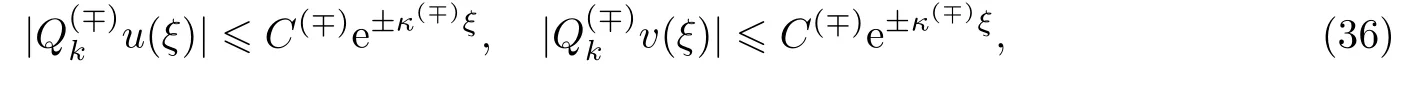
式中:常数C(∓)和κ(∓)随着和k的变化而变化.

注意函数表达式中包含未知量pk,k≥0.利用连续缝接条件v(x,ε)在间断点x0处连续来求解,即

得

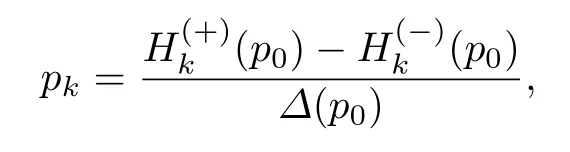
式中:

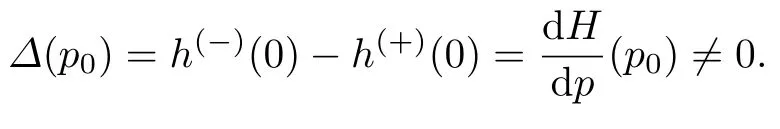
因此,构造了问题(30)的解(u(x,ε),v(x,ε))的n+1阶渐近展开式

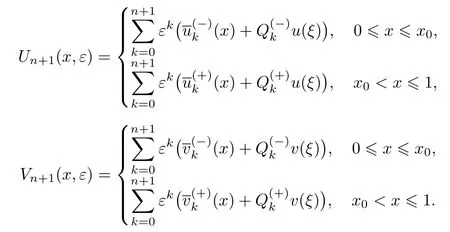
定理4如果满足条件17～21,那么,当ε＞0充分小时,问题(30)存在连续解(u(x,ε),v(x,ε)),且满足

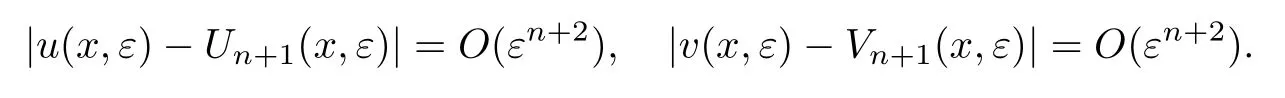
3 一类分段光滑二阶Tikhonov系统Dirichlet问题的渐近解

考虑如下奇异摄动问题[78]:

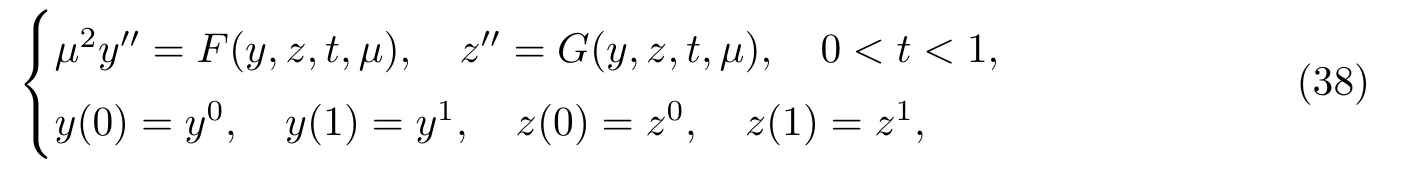
式中:0＜µ≪1为小参数.设t0为给定值并满足0＜t0＜1,函数F(y,z,t,µ)的表达式为

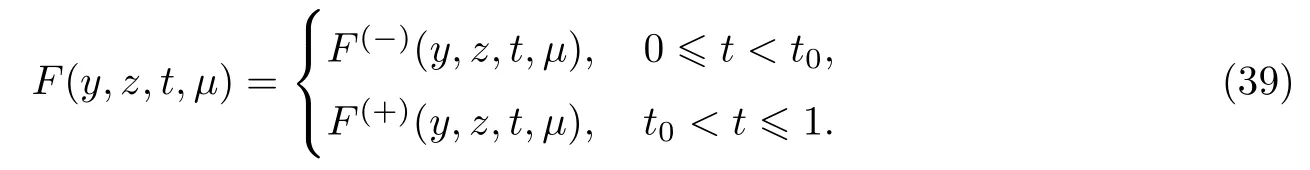
易见,问题(38)～(39)的解(y(t,µ),z(t,µ))满足(y(t,µ),z(t,µ))∈C1[0,1]∩(C2(0,t0)∪C2(t0,1)).

假设如下条件成立.

条件22假设函数F(−)(y,z,t,µ)在D1={(y,z,t,µ)||y|≤l,|z|≤l,t∈[0,t0]}上充分光滑;函数F(+)(y,z,t,µ)在D2={(y,z,t,µ)||y|≤l,|z|≤l,t∈[t0,1]}上充分光滑,且F(−)(y,z,t0,µ)̸=F(+)(y,z,t0,µ),即函数F(y,x,t,µ)在t=t0点联系,其中l是大于0的常数.函数G(y,z,t,µ)在D1∪D2上充分光滑.

条件23假设退化方程F(y,z,t,0)=0在D内有孤立解,

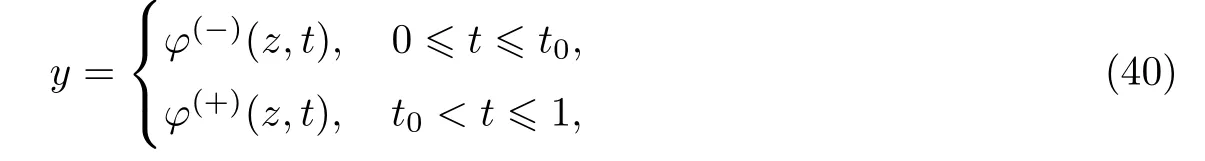
且在D上φ(−)(z,t0)̸=φ(+)(z,t0).同时,假设如下2个问题:

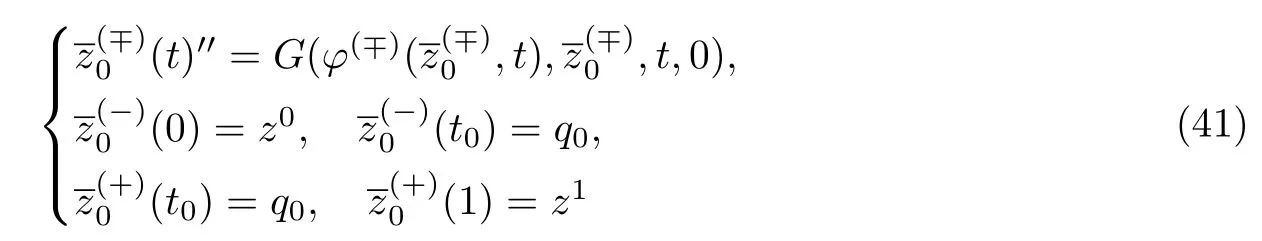
条件24假设以下2个问题:

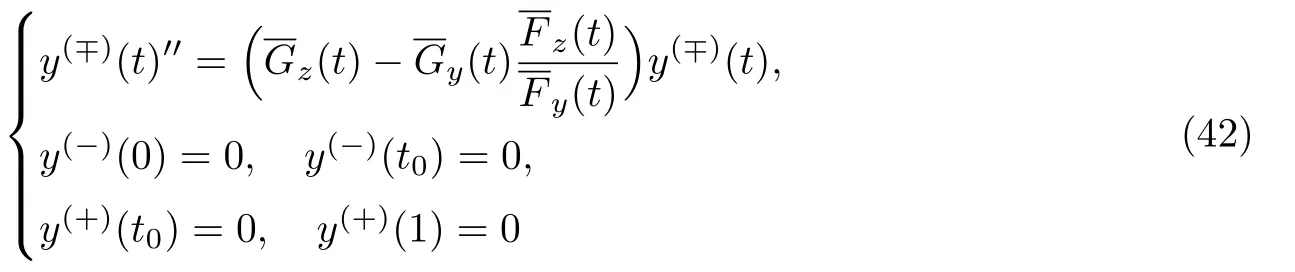
有零解.

条件25假设＞0,0≤t≤1.

将原问题以t=t0为界分为2个辅助问题,分别记为左问题和右问题,分别运用边界层函数法构造类似第2节的解的渐近展开式并进行光滑缝接,为函数y(t)和z(t)增加标记“–”(对左问题而言记为y(−)(t))和“+”(对右问题而言记为y(+)(t)).假设问题的解在t=t0点处的值为

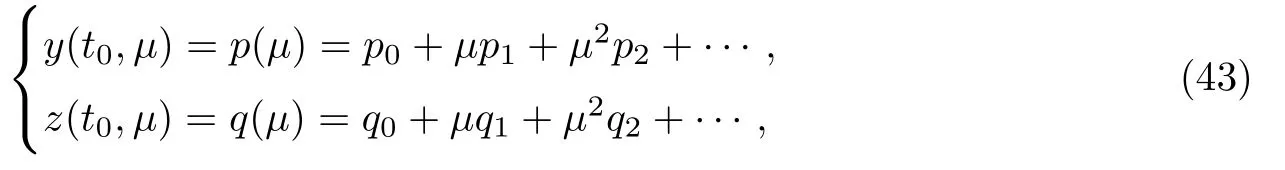
式中:pi,qi为待定系数,i∈N.

为了确定内部层的首项,考虑当t=t0时的辅助问题

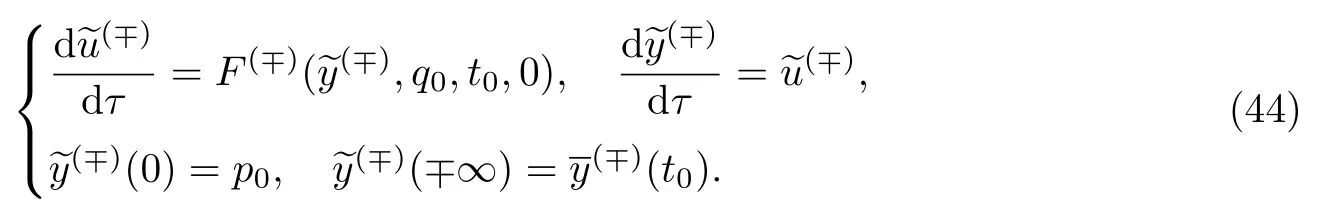
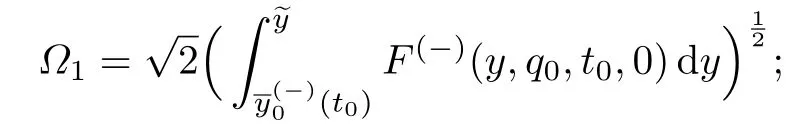
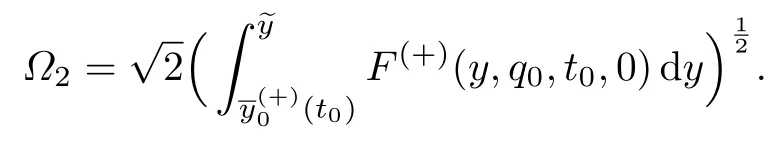
条件26假设和为非空集,即

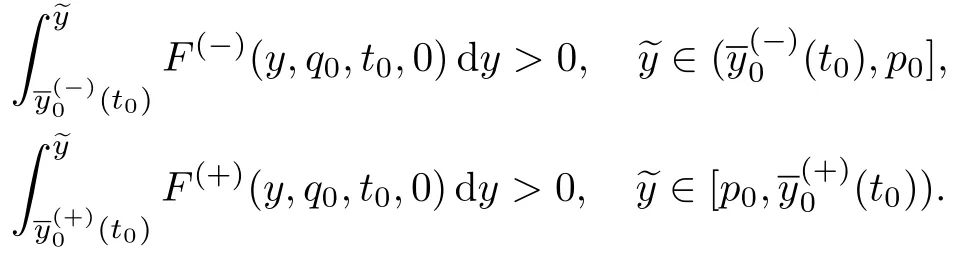
条件27假设H2(q0)=0存在解,且

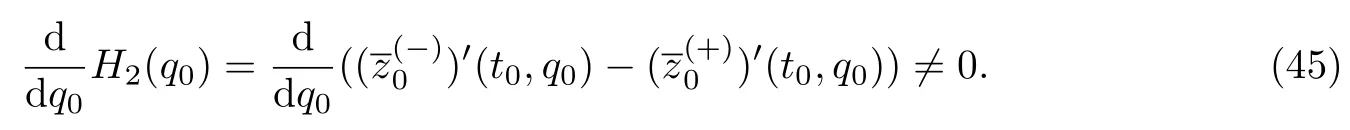
同理,为了确定边界层项的首项,考虑当t=0和t=1时的辅助问题

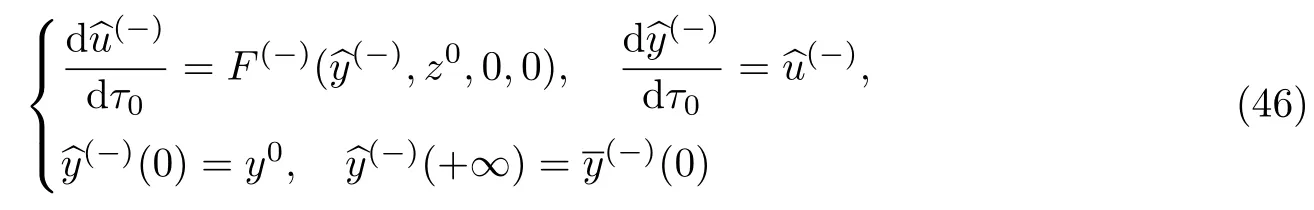
和

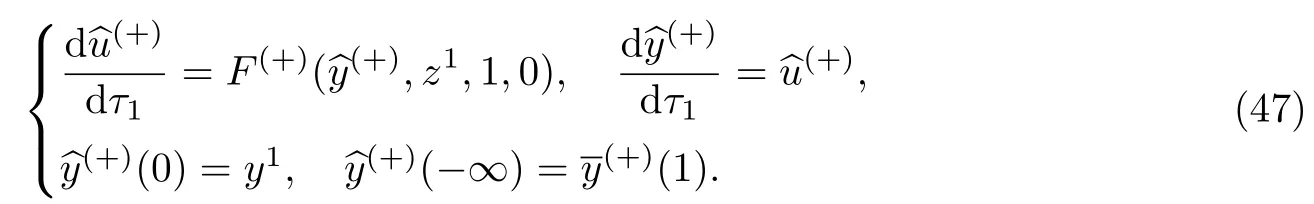
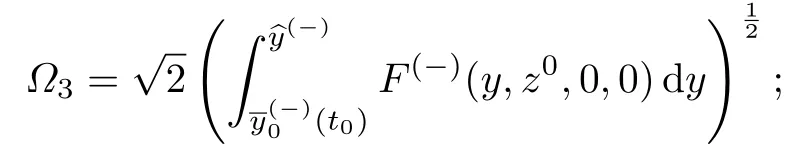
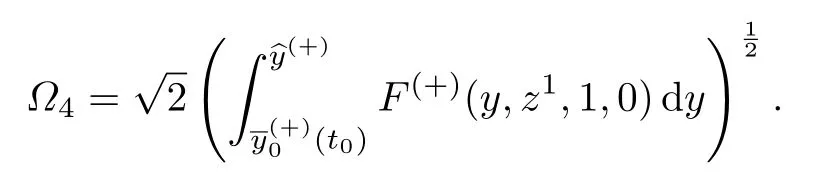
问题(46)和(47)的可解性条件为边值位于相应退化方程解的影响域内,等价于如下条件.

条件28假设和为非空集,即

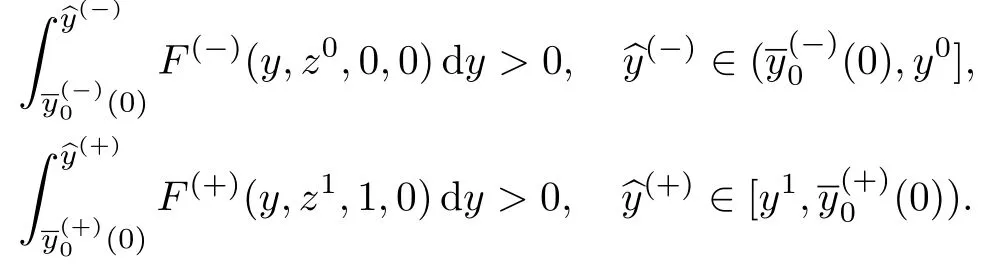
引理1对任意的k≥0,有

由引理1可求得所有的pk与qk.因此,可以得到问题(38)解的渐近展开式

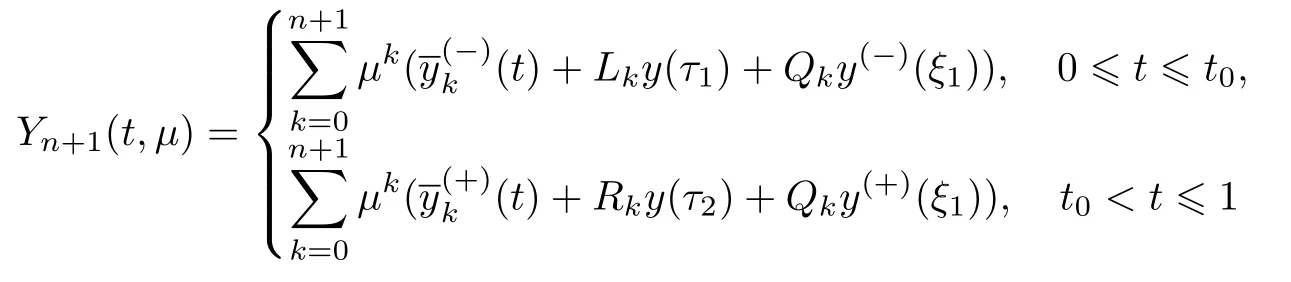
和

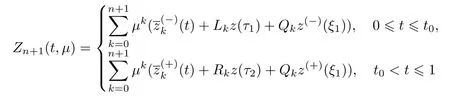
满足如下定理.

定理5如果满足条件22～27,则问题(38)在[0,1]的解存在,且满足

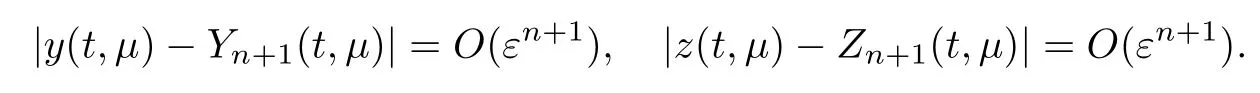
4 右端不连续奇异摄动抛物方程

4.1 右端不连续奇异摄动反应扩散方程

考虑奇异摄动反应扩散方程[79]

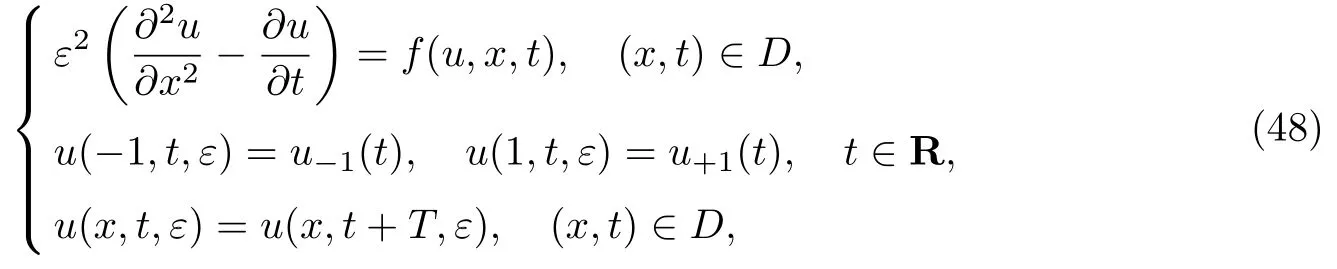
式中:D={(x,t)∈R2|-1＜x＜1,t∈R};ε＞0为小参数;T＞0为给定周期.假设存在T-周期函数x=h(t),将区域D分成如下2个部分:

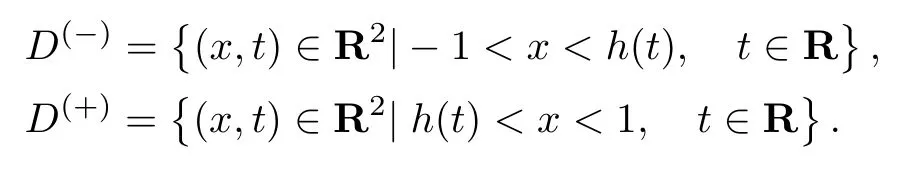
为了研究问题(48),需要先给出如下条件.

条件29方程(48)的右端函数f(u,x,t)具有如下形式:

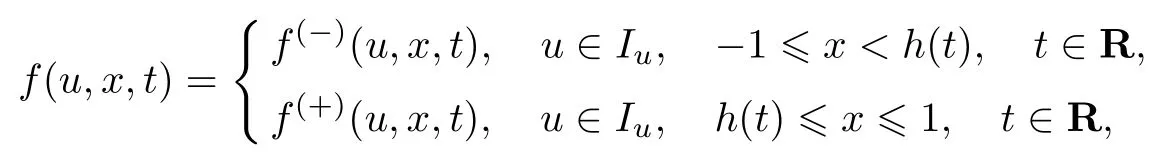
式中:函数f(−)(u,x,t)和f(+)(u,x,t)分别为区域和上充分光滑的T-周期函数,并且函数f(u,x,t)在曲线x=h(t)上不连续,即

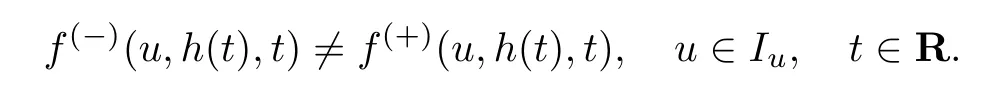
边界条件u−1(t)和u+1(t)也是充分光滑的T-周期函数.

条件30假设退化方程f(∓)(u,x,t)在区域和上分别有孤立的T-周期解u=φ(∓)(x,t).并且,在曲线x=h(t)上,不等式φ(−)(h(t),t)＜φ(+)(h(t),t),t∈R成立.

条件31假设函数f(∓)(u,x,t)满足如下不等式:

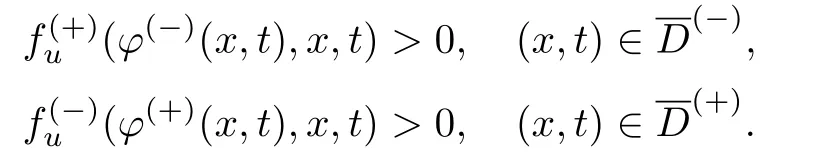
考虑如下辅助系统:

式中:x和t为参数.根据条件30和31,对任意固定的x,(φ(∓)(x,t),0)为鞍点型平衡点.因此,对任意固定的x,在平衡点(φ(−)(x,t),0)附近存在稳定流形和不稳定流形,

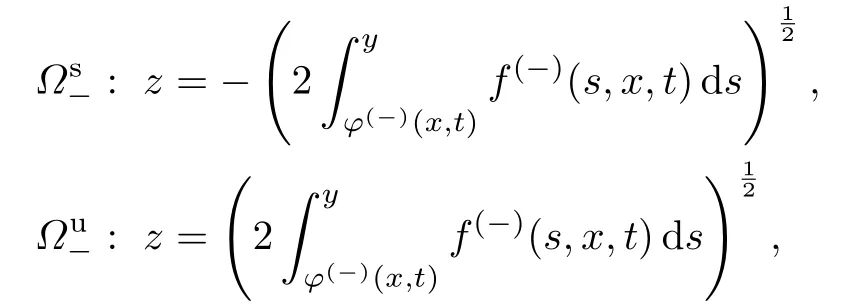
并且,在平衡点(φ(+)(x,t),0)附近存在稳定流形和不稳定流形:

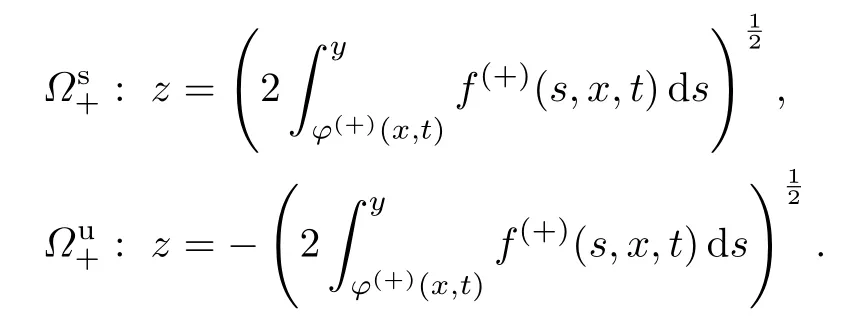
为了确定x=-1和x=1邻域内的边界层函数首项,需要研究在x=-1的边值问题

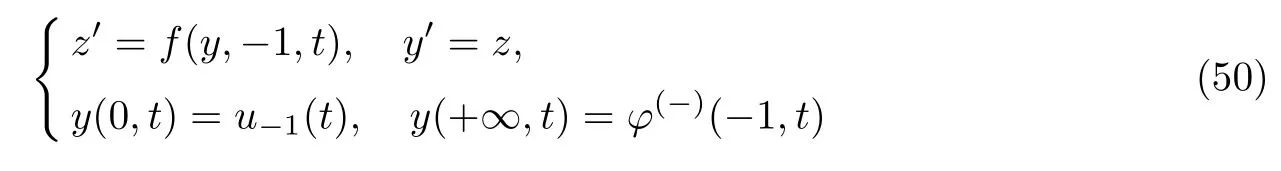
和在x=1的边值问题

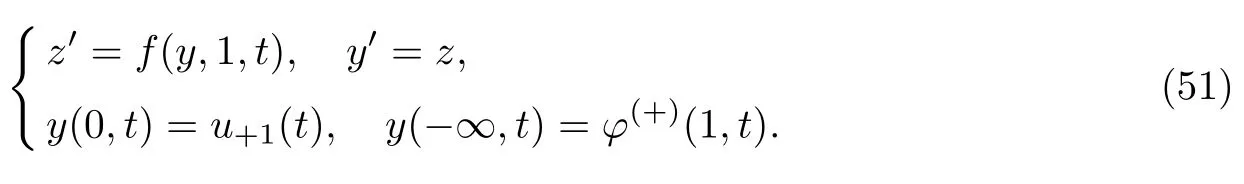
因此,问题(50)和(51)的可解性条件为边值条件u−1(t)和u+1(t)在对应平衡点的吸引域内.

条件32假设在相平面(y,z)中,垂线y=u−1(t)与平衡点(φ(−)(-1,t),0)的稳定流形横截相交,并且垂线y=u+1(t)与平衡点(φ(+)(1,t),0)的稳定流形横截相交,即

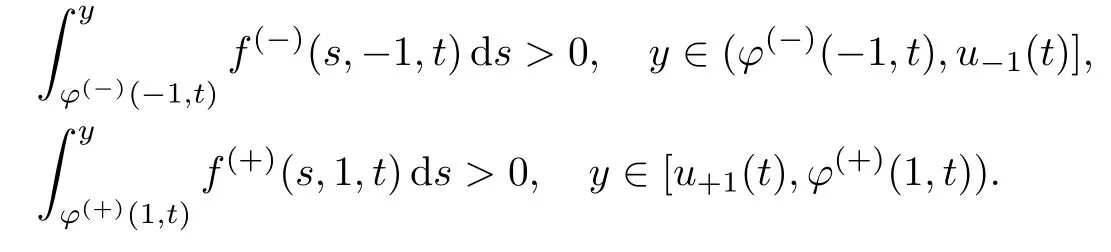
为了确定内部层函数的首项,需要研究在x=h(t)的边值问题:

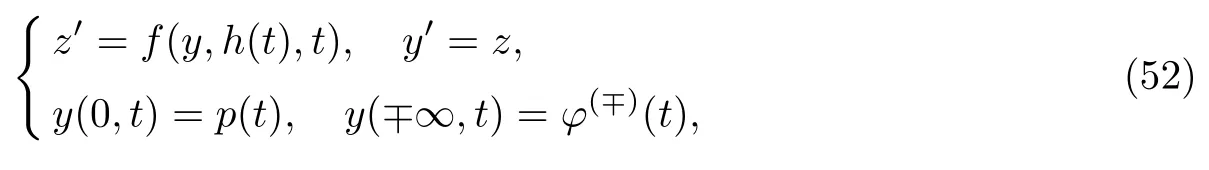
式中:φ(∓)(t)=φ(∓)(h(t),t)和p(t)∈(φ(−)(t),φ(+)(t))为待定函数.类似问题(50)和(51),问题(52)的可解性条件如下.

条件33假设在相平面(y,z)上,对任意的p(t)∈(φ(−)(t),φ(+)(t)),垂线y=p分别与平衡点(φ(−)(t),0)的不稳定流行和平衡点(φ(+)(t),0)的稳定流形横截相交,即

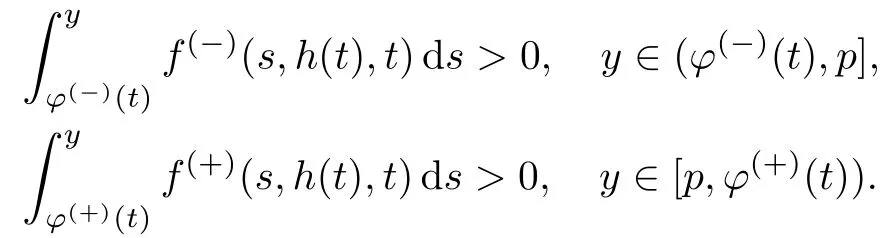
令

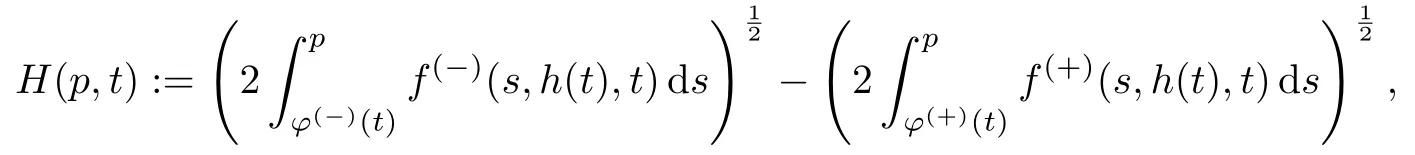
下面不等式成立.

条件34方程H(p,t)=0有唯一解p=p0(t),p0(t)∈(φ(−)(t),φ(+)(t)),并且

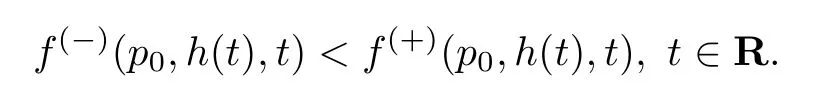
易见,方程H(p,t)=0可以化简为

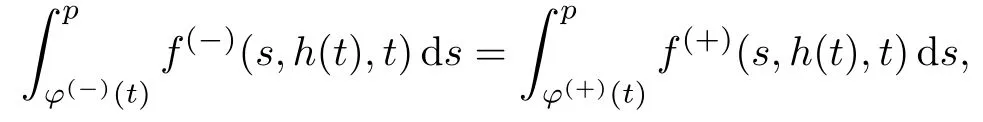
并且在p=p0(t)处,函数H(p,t)有如下导数形式:

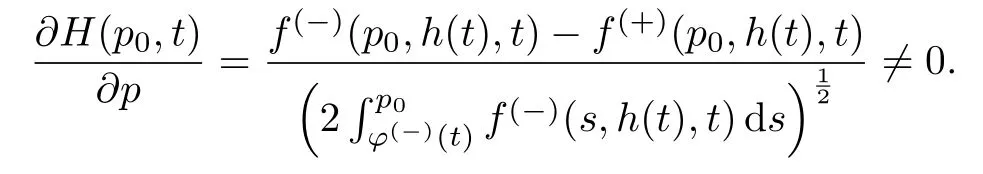
本课题组的目标是求解问题(48)具有内部层和边界层的周期解u(x,t,ε),其中内部层位于曲线x=h(t)的邻域内,边界层位于边界x=-1和x=1的领域内.而且,可以证明周期解在区域D(−)趋向于曲面u=φ(−)(x,t);在区域D(+)趋向与曲面u=φ(+)(x,t).因此,首先构造周期解的渐近展开式

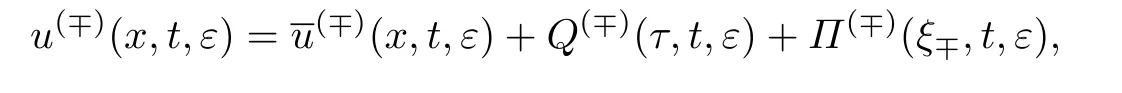
式中:

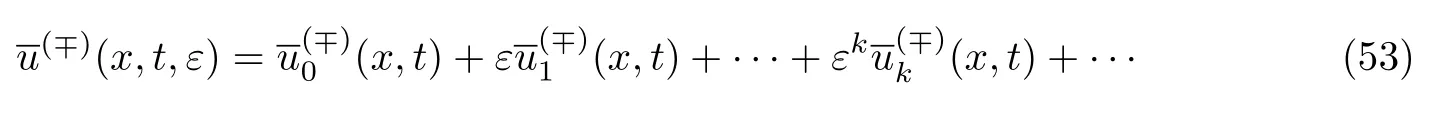
是正则项;

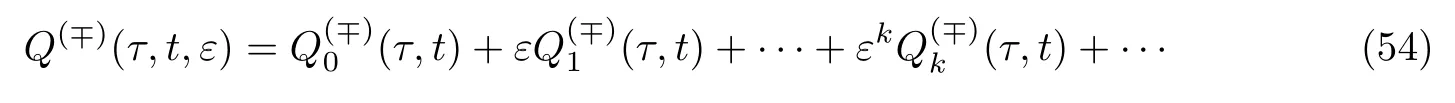
是曲线x=h(t)邻域内的内部层项,并且满足和0(i≥0),这里.

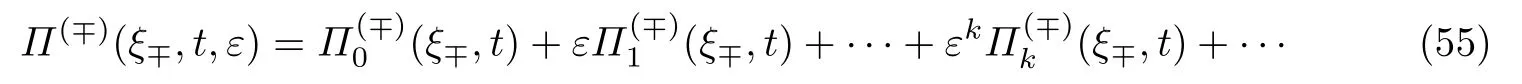
是边界x=-1和x=1邻域内的边界层项,满足和=0,i≥0,这里和

为了确定周期解的渐进展开式,考虑如下2个问题:

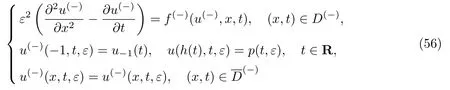
和

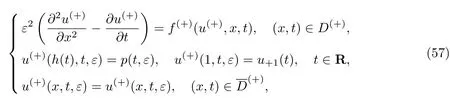
式中：p(t,ε)为待定函数,具体表达式为

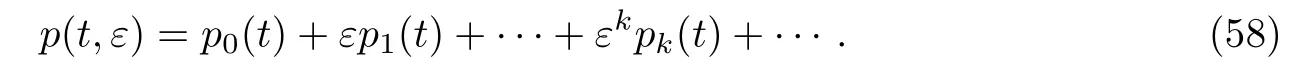
根据边界层函数法,将渐近展开式代入问题(56)和(57),并按不同尺度x,τ和ξ∓分离,得到确定正则项、内部层项和边界层项Π(∓)(ξ∓,t,ε)的方程,再将所得到的方程左右两端按小参数ε展开并比较同次幂,可以得到确定和,i=0,1,···的方程.因此,运用假设条件29～32求解所得到的方程,因此正则项中ε的各项系数为

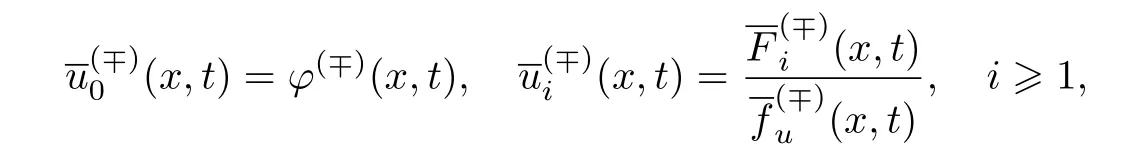
内部层项中ε的各项系数如下.

当i=0时,首项Q(∓)0由条件32唯一确定,且满足指数衰减性,即

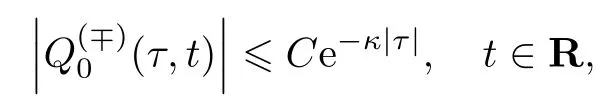
式中:κ和C为与小参数ε无关的正常数.

当i≥1时,

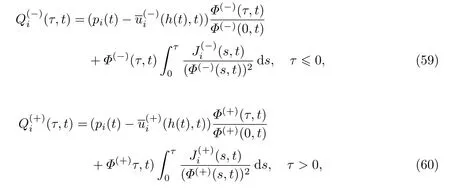
式中:

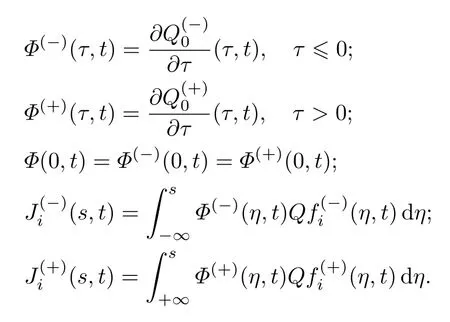
当i=0时,比较光滑缝接条件两边ε0系数可以得到

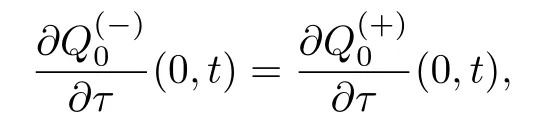
即

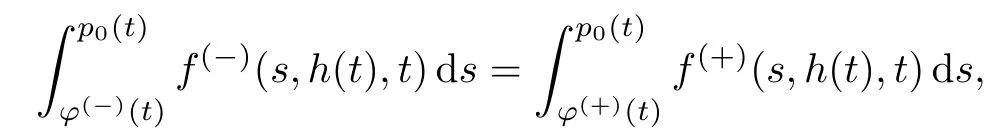
由条件34可知函数p0(t)是唯一确定的.

当i≥0时,比较光滑缝接条件两边εk系数可以得到

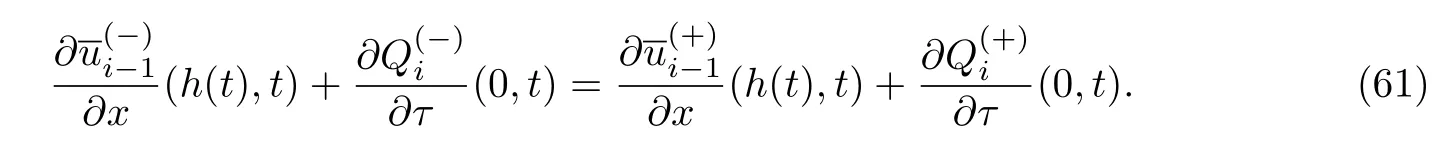
求解方程可以得到pi(t)的表达式

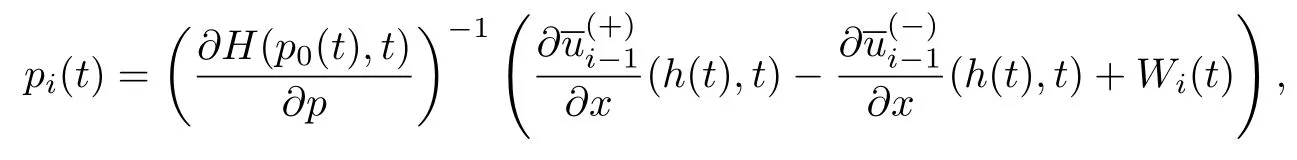
式中:

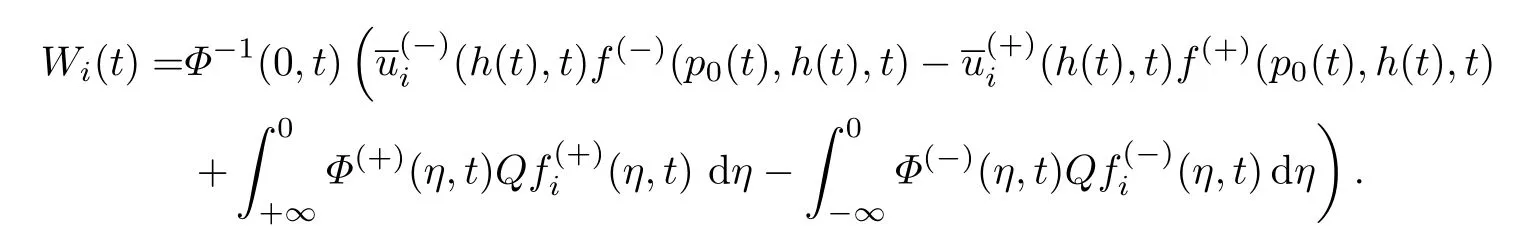
类似可得边界层项中ε的各项系数.因此可以构造周期解u(x,t,ε)的n+1阶渐近展开式

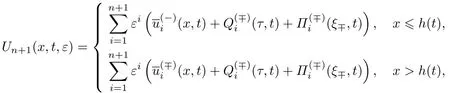
并得到如下定理.

定理6如果满足条件29～34,那么对充分小的ε＞0,问题(48)的周期解u(x,t,ε)存在,且满足余项估计

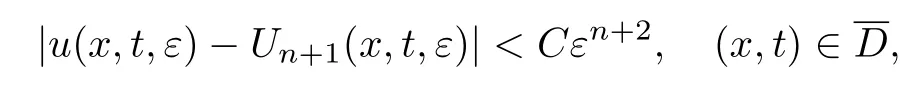
式中:C为与小参数ε无关的正常数.

4.2 右端不连续的奇异摄动反应扩散对流方程

考虑如下奇异摄动反应扩散对流方程[80]:

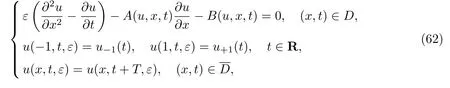
式中:

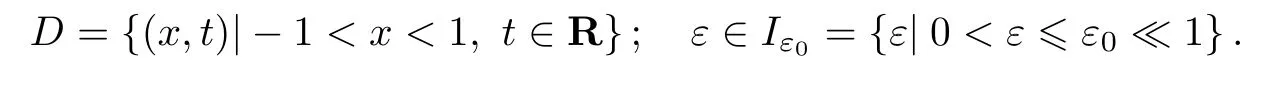
假设函数u−1(t)和u+1(t)是充分光滑的T-周期函数,且存在T-周期函数x=h(t),t∈R将区域D分成D(−)和D(+)2个部分:

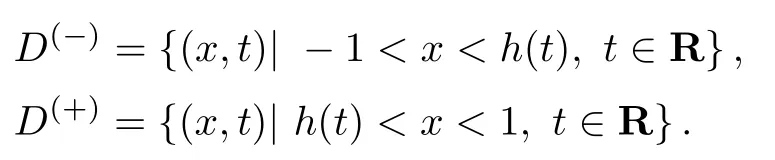
假设如下条件成立.

条件35假设函数A(u,x,t)和B(u,x,t)具有如下表达式

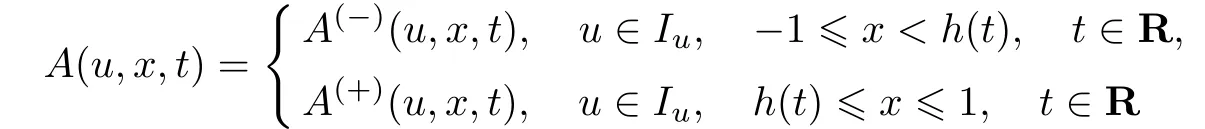
和

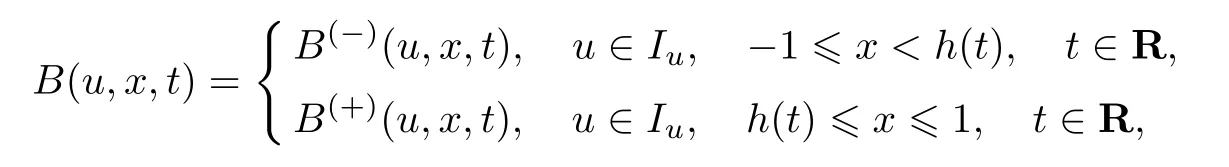
式中:Iu为未知函数u(x,t,ε)的取值区间;函数A(−)(u,x,t)和A(+)(u,x,t)分别为区域和上充分光滑的T-周期函数;函数B(∓)(u,x,t)的定义与A(∓)(u,x,t)相似.并且,函数A(u,x,t)和B(u,x,t)在曲线x=h(t),t∈R上间断.

令ε=0可以得到如下退化问题:

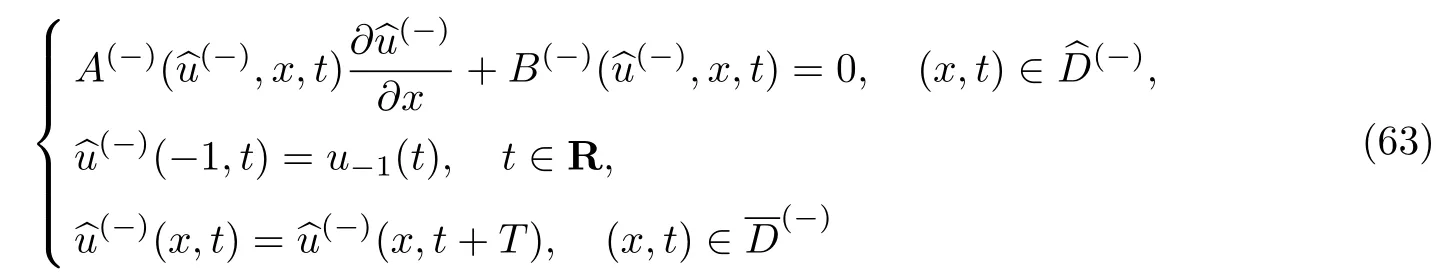
和

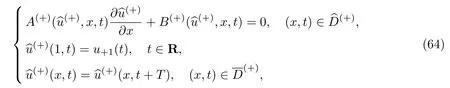
式中:t为参数;.

条件36假设退化问题(63)和(64)分别有孤立的T-周期解和φ(+)(x,t),并且在曲线x=h(t),t∈R上,不等式φ(−)(h(t),t)＜φ(+)(h(t),t),t∈R成立.

条件37假设函数A(u,x,t)满足下面不等式:

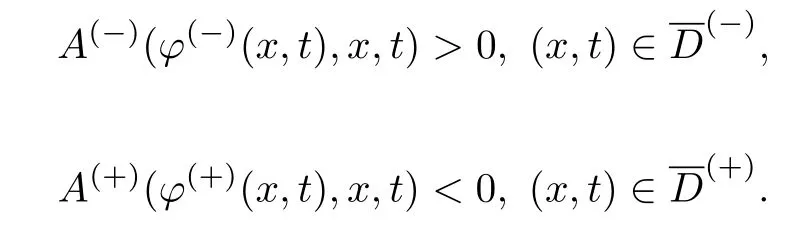
记

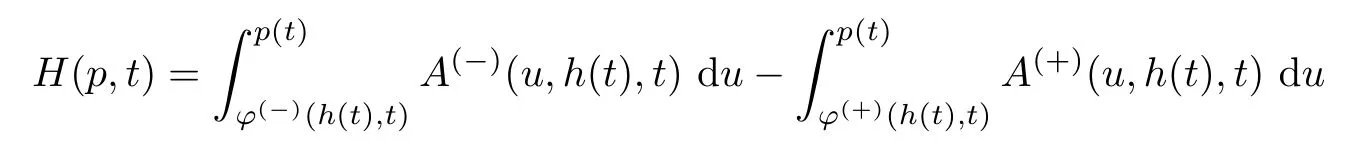
满足如下条件.

条件38方程H(p,t)=0有T-周期解p=p0(t)满足φ(−)(h(t),t)＜p0(t)＜φ(+)(h(t),t),并且对任意的s∈(φ(−)(h(t),t),φ(+)(h(t),t)),t∈R有.假设下面的不等式成立,

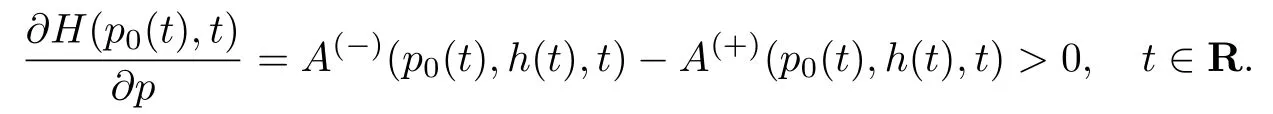
注意到退化问题(63)和(64)的解满足边值条件,因此我们的目标是求解问题(62)具有内部层的周期解u(x,t,ε),其中内部层位于曲线x=h(t),t∈R的邻域内.构造周期解的渐近展开式为

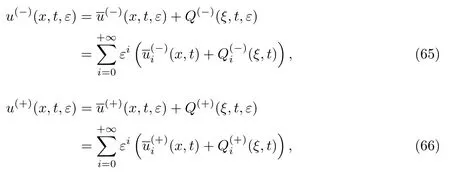
类似于4.1节,运用边界层函数法可以确定渐近展开式(65)和(66)中的表达式.

正则项中ε的各项系数为

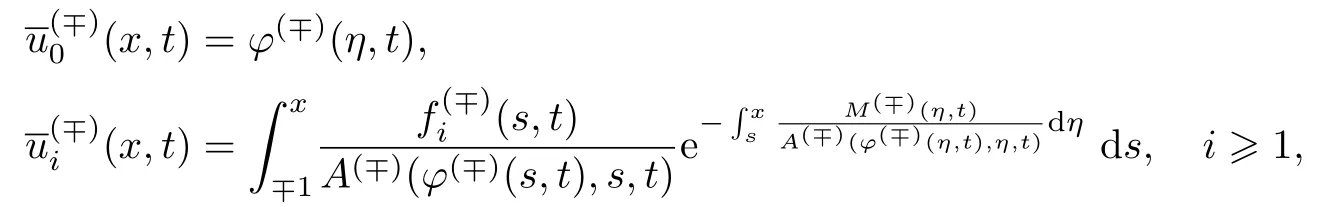
内部项中ε的各项系数如下.

当i=0时,根据条件36和37,可以唯一确定函数,并且满足指数衰减性,即

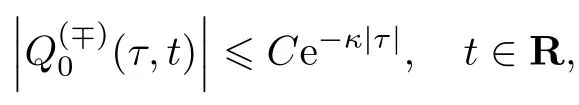
式中:κ和C为与小参数ε无关的正常数.

当i≥1时,

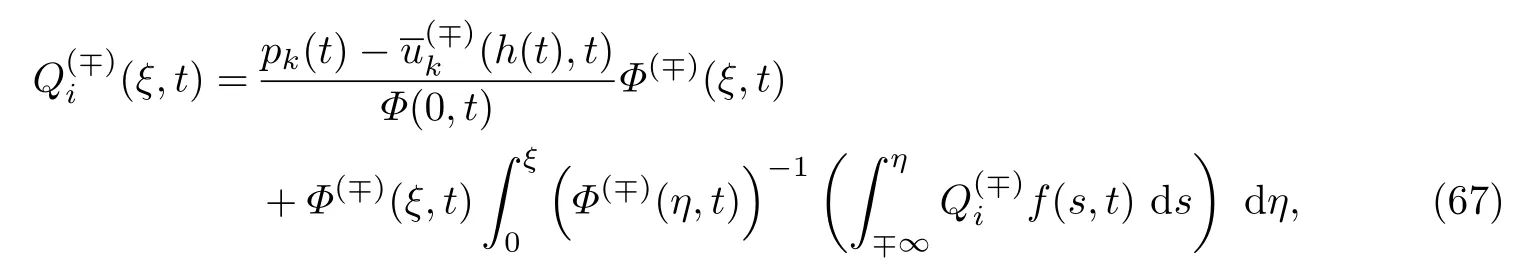
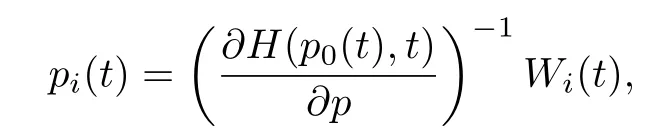
式中:

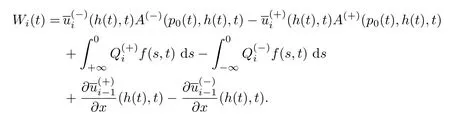
因此,可以构造周期解u(x,t,ε)的n+1阶渐近展开式

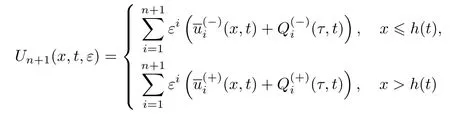
满足如下定理.

定理7如果满足条件35～38,那么对充分小的ε＞0,问题(62)的周期解u(x,t,ε)存在并且满足余项估计

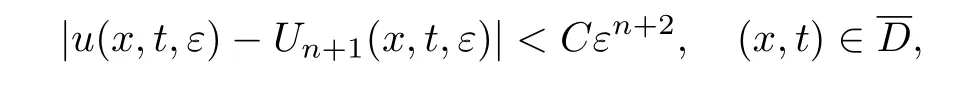
式中:C为与小参数ε无关的正常数.

进一步,运用微分不等式方法可以得到周期解u(x,t,ε)的稳定性.

定理8如果满足条件35～38,那么对充分小的ε＞0,问题(62)的周期解u(x,t,ε)是局部渐近稳定的.

5 结束语

目前,被人们新发现的奇异摄动现象,如多层现象、层套层现象以及非指数式衰减的边界层现象等,在右端不连续奇摄动系统中相继出现.针对这些新问题,传统的边界层函数法已不再行之有效,因此迫切需要去探索新的理论和新的解决方法.其中的原因是,由于不连续性,非线性奇异摄动系统的退化系统也是不连续的,这是最“常见”的情况,因此在不同区间上的退化解可以看成是组成真解的主要部分.如果在间断曲线或间断曲面处产生稳定性交替,则常常会和转点打交道.现在,对右端不连续奇异摄动系统的研究刚刚起步,仅停留在低维奇异摄动系统，尚未见到研究高维奇异摄动系统或者高维Tikhonov系统的论文.而对转点问题的研究也大多停留在二阶线性系统,即通常所说的线性转点问题,对非线性转点的研究也无一般方法可循.

纵观国内外研究现状,对上述问题的研究并不多见,已发表的论文也只能处理个案.这类问题的共同难点在于:①在间断曲线或间断曲面附近奇异摄动系统的动力学行为非常复杂,常常会出现稳定性交替,使得渐近解的表达形式未知,从而不能套用Tikhonov极限定理和Vasil’eva渐近展开定理;②如果在间断曲线或间断曲面上是非法向双曲的,则Fenichel几何奇异摄动理论也不能用,也就无法知道在间断曲线或间断曲面附近问题的解是否存在.