基于多数据融合的室内环境模糊综合评价

向朝兴, 茅 健

(上海工程技术大学 机械与汽车工程学院, 上海 201620)

随着经济的发展,人们对良好环境的追求也更加迫切,室内作为人们日常生活的重要场所,其环境质量也受到越来越多的关注.室内环境的好坏直接影响到人们的生活,甲醛、室内有机气态物质(TVOC)等浓度(质量浓度(ρ),全文同)超标对人体的危害非常巨大,因此,能时刻掌握室内环境状况,对室内环境质量进行评价是非常重要的,这样能直观地获得环境的优良状况,并为当前环境决策提供依据.

目前对空气质量(IAQ)的评价方法主要有客观评价、主观评价和主客观结合.客观评价是以空气中污染物浓度指标为依据对室内空气进行评价,主观评价则是通过人对室内环境的主观感受进行描述后判断[1].在客观评价中,张晓亮等[2]采用多传感器数据融合直接与模糊理论结合的方法进行环境评价,优点是能够快速进行评价并获取评价结果,缺点是没有考虑到人对环境的主观感受.故在室内环境评价中常以主观评价为主,Melikov等[3]利用呼吸热人体模型对室内空气品质进行优劣评价,这种方法是通过模拟人与环境接触途径的呼吸系统,并用一些仪器对人体所感知、所呼吸的空气品质进行综合评价.主观评价的方法多数为层次分析法,此方法将人的主观思维做定量处理,得出的结论很大程度上有主观臆断性.李明海等[4]在层次分析法的基础上运用模糊评价方法,对室内空气质量进行评价,表明模糊综合评价具有结果清晰以及系统性较强的优点,缺点是人的主观感受较弱,并且该模型没有针对性地进行环境因素分析.刘鸣等[5]认为模糊综合评价法能够综合考虑影响因素,优点是借助隶属函数和权重系数能够准确地体现室内环境品质在分级划分上的模糊性及变化的连续性,缺点是因素分析考虑不全.

针对模糊综合评价模型的不足,本文提出基于多数据融合的环境模糊综合评价方法.对于环境因素考虑不全的问题,采用多传感器进行数据采集和融合,获得室内多环境因素;对缺乏人体主观感受的问题,本文引入韦伯—费希纳定律,建立符合人体感受的评价标准,并结合模糊理论选取合适模糊集,最终建立模糊综合评价模型.

1 多传感器数据采集

1.1 数据预处理

传感器获得的数据往往是随机的,并不完全都是正确的,且很可能出现异常值,异常值会严重影响后面数据统计的准确性,产生较大误差,从而造成最后结果与预想状态严重偏离.本文采用箱线图对数据进行检测,它由5个数据统计量组成:最小值Xmin、下四分位数Q1、中位数Q2、上四分位数Q3和最大值Xmax.

将待统计的数据由小到大进行排列X:{x1,x2,…,xn},Q1为第25%位数据,Q2为第50%位数据,Q3为第75%位数据,具体表示为

(1)

式中,IQR为四分位距.区间下边缘为Q1-1.5IQR,上边缘为Q3+1.5IQR.则在[Q1-1.5IQR,Q3+1.5IQR]上的值为正常值,区间以外的值被视为异常值,应忽略.

使用箱线图对数据分布进行描述,异常值清晰可见.经验表明该标准的选取在处理批量数据时具有较高的鲁棒性[6].

1.2 分批估计理论数据处理

在检测过程中,传感器性能上的差别或外界的干扰因素,可能会对测量结果产生较大误差.为了减小误差,提高精度,采用分批估计理论对检测数据进行融合处理[7].分批估计理论是对同一个检测量在不同位置的测量值进行融合处理的一种算法.对于一组特定传感器,首先得出一致性测量数据;然后将某一特定传感器在不同位置所测数据分组.分组太多会降低数据测量精度,故本文选择将数据分为两组.第1组数据为t11,t12,…,t1m,m∈N;第2组数据为t21,t22,…,t2n,n∈N.

(2)

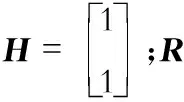
(3)

由分批理论导出数据融合值为

(4)

(5)

1.3 多传感器自适应加权融合

图1 多传感器自适应加权融合算法模型Fig.1 Multi-sensor adaptive weighted fusion algorithm model

(6)

因此总均方误差σ2为

(7)

式中:σ2为关于各加权因子的多元二次函数,根据多元函数求极值理论,可求出总均方误差最小时所对应的最优加权因子为

(8)

此时,对应的总均方误差最小值为

(9)

(10)

可得多传感器数据融合值为

(11)

2 模糊综合评价模型分析

2.1 建立环境评价标准

韦伯和费希纳用心理物理试验证明并推导出:对于中等强度刺激,人体产生的反应量S的大小与客观刺激量R的对数成正比,即存在韦伯—费希纳定律,公式为

S=klogR

(12)

式中:R为客观刺激量;S为人体产生的反应量;k为常数.

刺激物只有达到一定强度才能引起人的感觉,刚刚能引起感觉的最小刺激量,称为感觉阈值.根据韦伯—费希纳定律,人们对此浓度的感觉量为

LOi=kilogXci

(13)

式中:Xci为某项环境参数Xi的阈值;ki为环境参数Xi的常数;LOi为Xci对应的感觉量.

以二氧化碳(CO2)参数为例,采用文献[9]中所提出的舒适性评价分度方法,建立CO2评价分指数模型.正常空气中CO2浓度(体积分数(φ),全文同)为300～400 ppm(ppm为每百万个空气分子中CO2分子的数量),其阈值为485,当室内CO2浓度为1 000 ppm时,会引起室内人员较明显的不适,因此CO2评价分指数模型为

(14)

可得出PMVCO2为0、0.5、1.0、1.5和2.0时,对应的CO2浓度分别为:485、580、700和1 000 ppm.根据此方法可以建立多指标的评价标准,具体结果见表1.

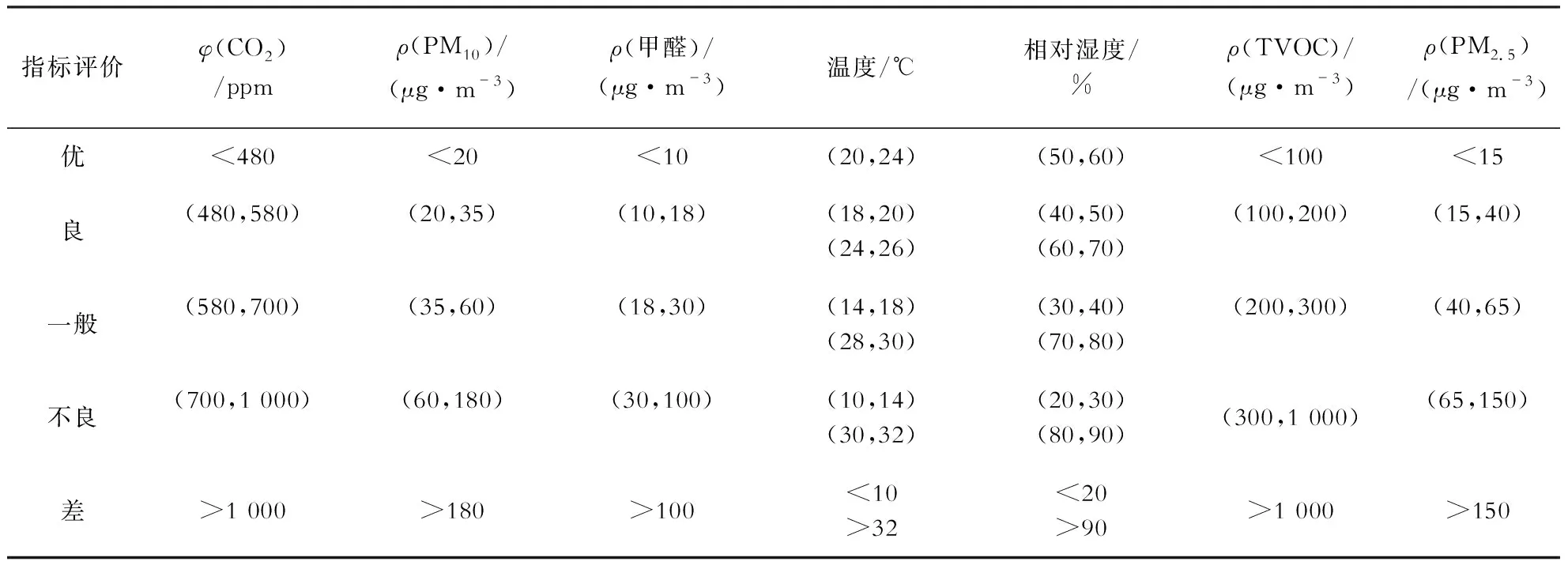
表1 环境因素评价标准Table 1 Environmental factor evaluation criteria

2.2 确定隶属函数

模糊因素集U=(u1,u2,u3),uk为对判决起作用的第k个模糊因素,设每个因素对应的权值构成模糊因素权集A=(α1,α2,α3),权值表示第k个因素对关联判决的影响程度[10].

(15)

线性函数f1(x)、f2(x)满足

(16)

其中,f1(x)、f2(x)的表达式由直线方程的两点式可得;指数α,β可由公式求得,公式为

故

(17)

同理可得

(18)

2.3 计算环境因素权重

应用层次分析法(AHP)分析环境因素权重,该方法的特点是定性分析与定量分析相结合,将人的主观判断用数量形式表达和处理.层次分析法的信息基础主要是人们对每一层次各因素的相对重要性给出的判断,这些判断用数值表示出来,写成矩阵形式即判断矩阵.

1) 确定判断矩阵B,在本研究中,采用1～9标度法来确定因素权重.

2) 计算判断矩阵的最大特征值.

计算判断矩阵B每一行元素的积,公式为

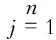
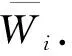
计算判断矩阵B最大特征值λmax,公式为

3) 对判断矩阵进行一致性检验.

计算一致性指标CI,公式为

(19)

计算一致性比率CR,公式为

(20)

式中,RI为平均随机一致性指标.根据相关算法,当CR<0.10时,认为判断矩阵的一致性是可以接受的,否则做适当修正.

将满足一致性检验的判断矩阵按列归一化,再

用算术平均法求权重ωi,公式为

(21)

用几何平均法求权重ωi,公式为

(22)

特征值法求权重,已知最大特征值λmax,求出对应特征向量进行归一化,即得到权重.

根据文献[4]建立判断矩阵,见表2.

表2 判断矩阵Table 2 Judgment matrix

计算判断矩阵的最大特征值为7.501 8,一致性指标CI=0.083 6,一致性比率CR=0.061 5<0.10,所以该判断矩阵B的一致性可以接受.由此计算出环境因素权重,见表3.

表3 环境因素权重Table 3 Weight of environmental factors

3 试验分析

3.1 数据来源

本次研究采用多传感器对某一室内空气环境因素(PM2.5,温度,相对湿度,PM10,TVOC,CO2,甲醛)进行数据采集,由于数据过多,在此只列出部分数据,采集数据见表4.

表4 部分原始数据Table 4 Part of original data

采用箱线图法进行数据处理,得到数据的取值范围见表5.符合表中取值范围的数据被保留,不符合的被去除.

表5 取值范围Table 5 Value range

将预处理后的数据进行分批估计处理,首先将传感器获得的一组数据进行分批,第1批数据为前50%的数据,第2批为后50%的数据.以温度数据为例,根据分批估计理论结合自适应加权融合算法,计算得出具体结果,见表6.

表6 多传感器融合的温度数据Table 6 Multi-sensor fusion of temperature data

根据此算法,可分别对其他环境因素进行融合,从而获得适当的融合值,具体融合结果见表7.

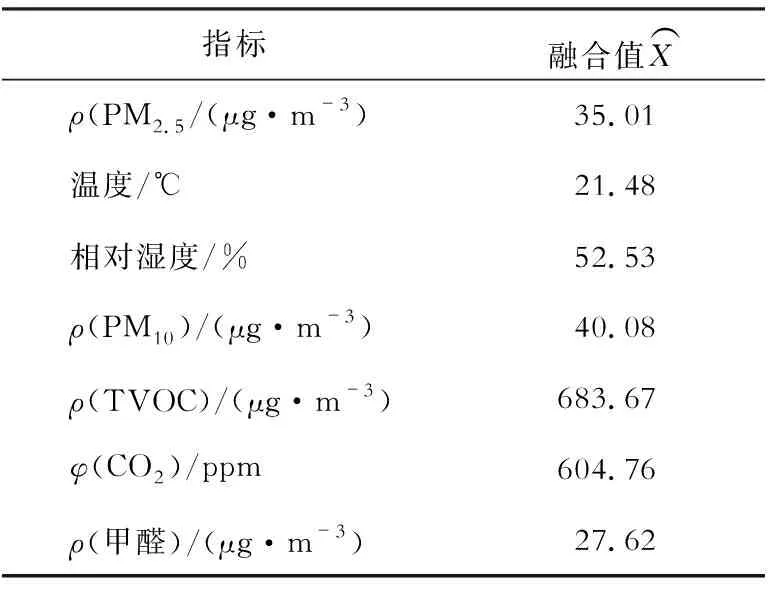
表7 各指标多传感器融合数据Table 7 Multi-sensor fusion data for each indicator

3.2 确定指标权重

根据表1,以甲醛参数为例,X=(0,+)为甲醛浓度所有值的集合,建立评价等级模糊集合{优、良、一般、不良、差},先求模糊集优的隶属函数,由式(15)

至式(18)可求得β=6.579,α=0,则模糊集优的隶属函数为

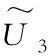
根据甲醛的隶属函数,算出表7中甲醛融合值的隶属度,再进行归一化,可得该值在每个模糊集中的隶属度权重,具体结果见表8.

表8 甲醛隶属度权重Table 8 Membership weight of formaldehyde

根据此算法,可以相继得出其他环境因素的隶属函数,从而求出隶属度权重,具体结果见表9.

表9 各指标隶属度权重Table 9 Membership weight of each indicator

3.3 模糊综合评价

应用层次分析法中的评价表,进行模糊综合评价,见表10.

表10 模糊综合评价Table 10 Fuzzy comprehensive evaluation

方案i,i∈(1,n)的得分为

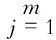
(23)

结合表3、表9和式(23),可以求出多传感器融合数据的模糊综合评价结果,见表11.

表11 环境因素模糊综合评价表Table 11 Fuzzy comprehensive evaluation of environmental factors

从而可得出每个评价标准的具体得分,结果见表12,环境因素权重分布如图2所示.

表12 评价结果Table 12 Evaluation result

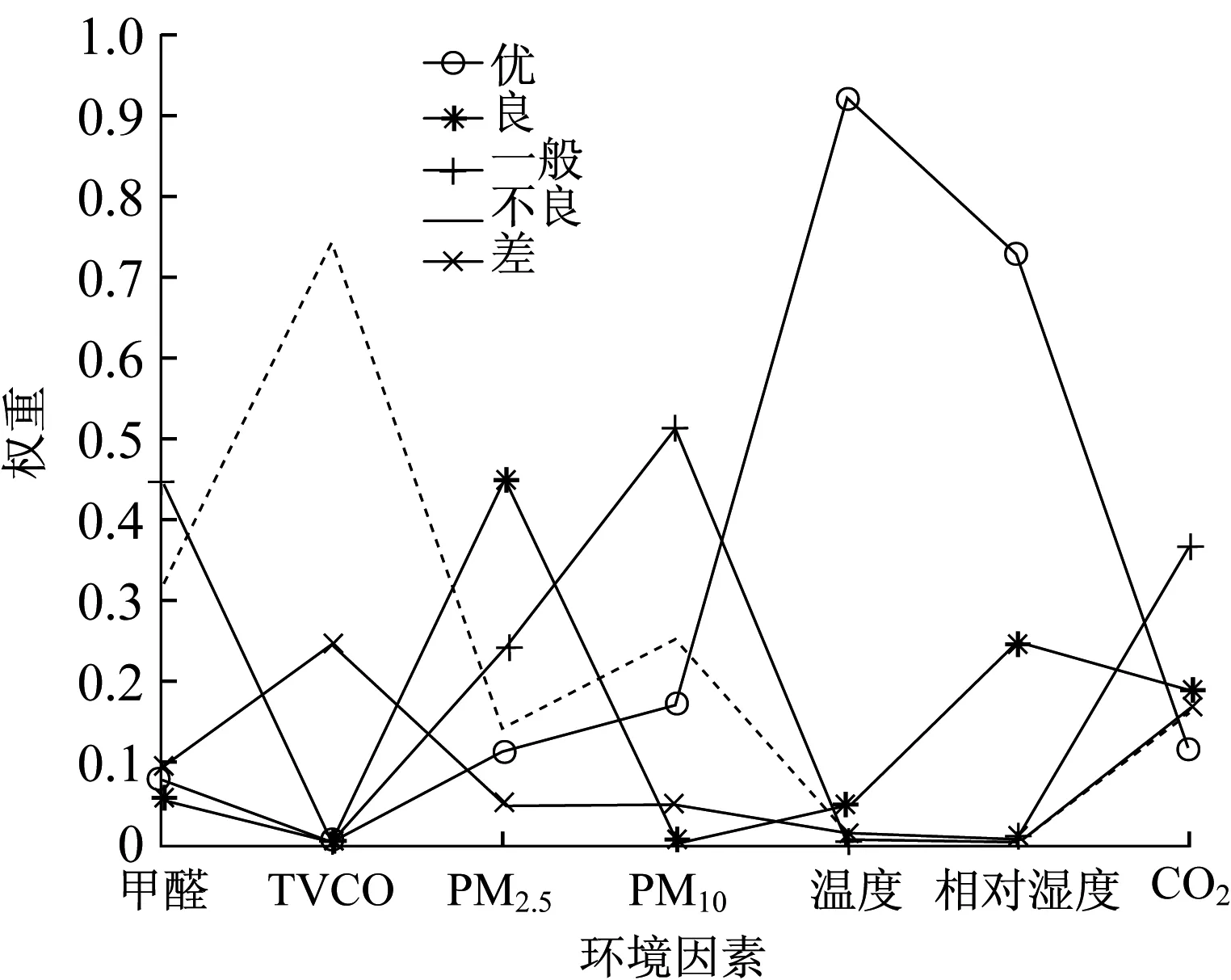
图2 环境因素权重分布Fig.2 Weight distribution of environmental factors

从评价结果可以看出,该室内环境品质不良,从图2中可以得出,影响评价结果最主要的因素是TVOC,其次是甲醛,不良和差这2个评价等级所占权重最高,而室内温度、相对湿度以及PM2.5浓度情况为优良,CO2和PM10的浓度稍微偏高,因此在室内管控时,应当着重注意室内TVOC、甲醛、PM10的排放,注意室内通风,做好室内环境清洁工作,防止人员在室内吸入过多的有害气体而中毒.综上所述,完善后的模糊综合评价模型应用于室内环境评价领域是科学的,评价结果准确、清晰,有利于室内环境规划设计和最大限度减少室内空气污染.

4 结 语

本文采用多传感器进行室内数据采集,避免了单一传感器的局限性,并采用数据融合技术对数据进行融合,通过模糊理论结合层次分析法,建立室内环境评价模型,对室内环境进行多环境因素分析.该评价模型能够直观的分析出当前室内环境因素的分布情况,对处于评价等级不良或差分布的环境因素,应当及时采取措施改善室内环境质量.该模型采用韦伯—费希纳定律并结合模糊理论,能够更加体现人对室内环境的真实感受,所得评价是真实可靠的,因此为解决室内环境评价问题提供了理论依据和指导意义.由于本文模型采用主观评价方法,具有一定的局限性,后续将引入客观评价方法做进一步研究.