HXD系列机车区间运行时分电算系统设计

霍艳忠, 武振锋, 李宁洲, 杨震宇

(1.集宁机务段 中国铁路呼和浩特局集团有限公司, 乌兰察布 012000;2.兰州交通大学 机电工程学院, 兰州 730070)

列车区间运行时分是编制列车运行图的基础参数,也是影响列车区间通过能力的主要因素之一[1-2].HXD系列机车是我国新一代交流传动货(客)运机车,主要包括HXD1、HXD2和HXD33个系列,具有持续功率高、运行速度快和牵引质量大等特点[3-4].HXD系列机车的诞生,不仅实现了中国铁路牵引技术从直流传动到交流传动的根本转换,还满足了铁路运输高速增长的要求.

在列车运行的整个区间,线路纵断面不可避免地存在平道和坡道,即存在线路的变坡点.而列车经过变坡点的速度值是计算列车在整个区间运行时分的重要依据.目前,对列车经过线路变坡点的速度计算主要有分析法和图解法[5].由于两种方法均采用试凑的方式,如果线路区间内存在大量的坡段,试凑的计算量将非常大,出现的误差也很大.同时,由于国家铁道行业标准TB/T 1407—1998《列车牵引计算规程》缺少HXD系列机车的各类基础数据,所以截至目前,关于HXD系列机车的牵引计算系统并不多见.

本文根据国家标准TB/T 1407.1—2018,设计了HXD系列机车区间运行时分电算系统,该系统可以较为准确、快速地计算出列车在牵引、惰行和制动工况下的区间运行时分,更好地分析列车实时运行状态[6].

1 列车牵引计算模型

列车牵引计算以力学为基础,所以计算列车区间运行时分首先要建立力学模型.列车牵引计算力学模型主要包括单质点模型和多质点模型[7-8].单质点模型与多质点模型相比较,具有简单易行,计算效率高的优点.同时,饶忠[9]分别采用单质点和多质点模型对列车运行时分进行了比较计算,结果表明两者的误差值很接近,鉴于以上原因,采用单质点力学模型研究列车区间运行时分时更加经济可行[10].列车单质点力学模型如图1所示.

图1 列车单质点力学模型Fig.1 Single particle mechanical model of train

图中:Wi为列车加算附加阻力;W0为列车基本阻力;B为列车制动力;N为线路对列车的支持力;G为列车重力;F为机车牵引力.

1.1 空旷平直线路列车单位合力

作用在列车上的单位合力是计算列车区间运行时分的重要依据.当列车通过变坡点时,采用单质点力学模型能够更好地分析列车单位合力的变化情况.列车在运行过程中,运行工况可以分为牵引、惰行和制动3种,单位合力计算公式分别为

(1)

(2)

c3=-[βc·(1 000ϑhφh)+

(3)

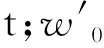
1.2 加算坡道列车单位合力

当列车通过坡道、曲线和隧道时,通常采用加算坡道的坡度千分数ij来反映复杂线路条件对列车单位合力的影响.列车以任意一种工况通过加算坡道时的单位合力公式为

ck=cp-ij

(4)

式中:k=1,2,3,分别为牵引、惰行和制动工况;ck为某工况下考虑线路加算坡道坡度千分数ij时的列车单位合力,N/kN;cp为列车在空旷平直线路上运行时每个速度间隔内平均速度所对应的单位合力,N/kN.

1.3 列车运动学方程

列车在速度间隔[v1,v2]所运行的距离可以表示为

(5)

列车在速度间隔[v1,v2]内的运行时间可以表示为

(6)

式中:v1、v2分别为列车在每个速度间隔的初速度和末速度,km/h.

列车经过不同坡段变坡点的速度值应满足条件

Si=∑ΔS+Es

(7)

式中:Si为线路实际坡段长度,m;∑ΔS为实际计算的每个速度间隔列车运行距离之和,m;Es为电算时所允许的距离误差,取±10 m.

列车在每个坡段的运行时间可表示为

ti=∑Δt

(8)

线路的多个坡段形成区间,列车通过整个区间的运行时间可表示为

t=∑ti

(9)

2 电算系统设计

2.1 数据库设计

列车区间运行时分计算涉及列车运行工况、机车、车辆以及闸瓦等多项数据.其中,列车运行工况包括牵引、惰性和制动3种;机车数据包括机车型号、机车计算质量、机车牵引力、机车单位基本阻力等;车辆数据包括车辆型号、牵引质量、车辆单位基本阻力等;闸瓦数据包括机车、车辆闸瓦的类型、换算闸瓦压力以及换算摩擦系数等.上述数据均来源于最新的国家标准[11],同时采用VB 6.0开发数据库应用系统,通过使用ADO对象访问数据,同时也可以在程序中浏览、编辑数据库中的各类数据.

2.2 算法设计

算法设计是列车区间运行时分电算系统中的重要环节.列车牵引电算可根据编组数据、线路数据及列车运行状态等信息,自动计算单位合力、单位时间步长内列车速度、距离、加速度等数据,结合数据信息与节时操纵策略自动进行工况调整,完成列车区间运行的仿真,最终输出速度与距离、时间与距离等数据表.根据所建立的列车单质点力学模型,3种工况下列车单位合力的算法流程如图2所示.

图2 列车单位合力算法流程图Fig.2 Algorithm flow chart of train unit resultant force

计算所得的列车单位合力数据供电算列车区间运行时分时调用.接着,建立电算系统的数学模型.数学模型是进行算法设计的基础,根据1.3节所提供的列车运动方程,结合列车运行状态和规律,进行列车区间运行时分的算法设计.其中,线路实际的坡段长度Si与实际计算的每个速度间隔列车运行距离之和∑ΔS之间的误差判断是系统算法的关键环节,本系统采用枚举法进行误差判断.列车区间运行时分算法流程如图3所示.

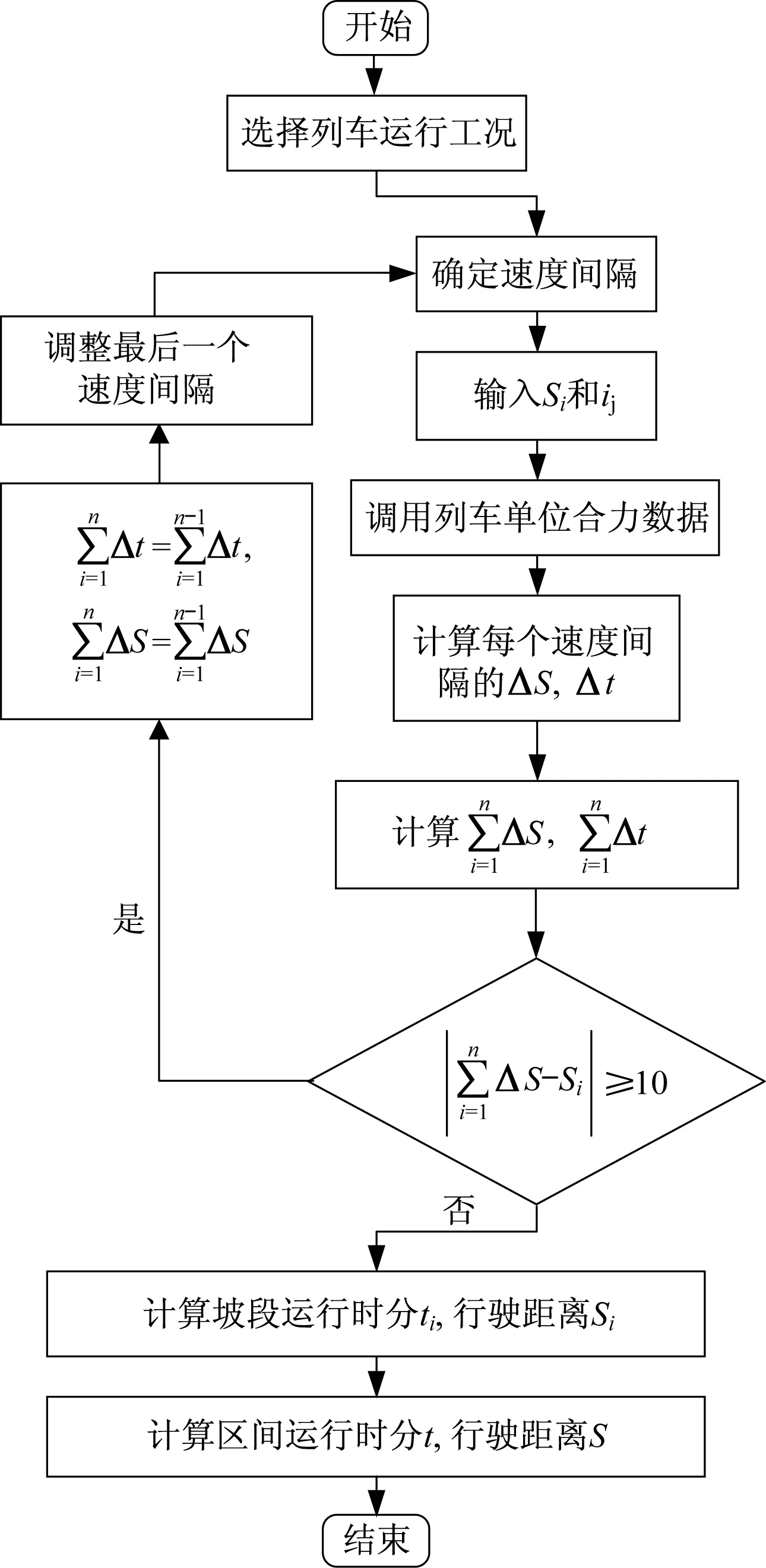
图3 列车区间运行时分算法流程图Fig.3 Algorithm flow chart of train running time in sections

2.3 界面设计

电算系统算法设计完成之后要进行电算系统的界面设计.电算系统界面输入部分包括选择机车型号、车辆型号和运行工况,输入机车数量、车辆质量、牵引质量、运行速度、坡度和坡长.输出部分包括列车单位合力、列车经过变坡点的速度、速度间隔运行时间与运行距离、区间运行距离以及区间运行时分等.电算过程中所得到的各类数据将以.dat文本格式存储在外部文件中,以便于计算时互相直接调用.

3 案例电算及分析

选取机车型号为HXD1C(轴质量25 t),单机牵引60辆滚动轴承重货车(轴质量23 t),牵引质量5 520 t,列车管定压为500 kPa,机车制动采用高摩合成闸片,车辆制动采用高摩合成闸瓦.

现以兰新铁路A-B区间(武威站至截河坝站)为例,进行列车区间运行时分的分析与计算.解算区间列车运行时分,需要对该区间内变坡点的速度进行试凑,区间内坡段数越多,试凑计算的工作量越大.为了提高计算效率,在不影响计算结果的情况下,可以对A-B区间内坡度相差不大的相邻坡段进行合并,即对A-B区间线路纵断面进行化简.化简方法是,用一个等效坡道和坡长,分别代替坡度相差不大的相邻坡道和坡长.其中,化简坡度i等于化简坡段的高度差与化简坡长之比,等效坡长为各段坡长之和.

A-B区间线路纵断面情况为:i1=0坡段,坡长为4 450 m;共计3个坡度相差不大的连续下坡坡段,i2,i3,i4分别为-1‰、-1.8‰、-3‰,坡长分别为485、260和995 m,连续下坡的高度差为-2.95 m;共计2个坡度相差不大的连续上坡坡段,i5,i6分别为2.8‰、3.7‰,坡长分别为1 870和840 m,连续上坡的高度差为8.67 m;i7=0坡段,坡长为1 980 m.

i1,i7=0坡段不需化简,分别对连续下坡坡段和连续上坡坡段进行化简.化简后A-B区间的线路纵断面如图4所示.

图4 区间线路纵断面图Fig.4 Tack profile of section

3.1 3种工况列车单位合力计算

图5 10 km/h列车单位合力电算结果Fig.5 Computerized results of train unit resultant force at 10 km/h

经过统计,列车以不同速度v运行时的牵引、惰行和制动3种工况单位合力计算结果见表1.

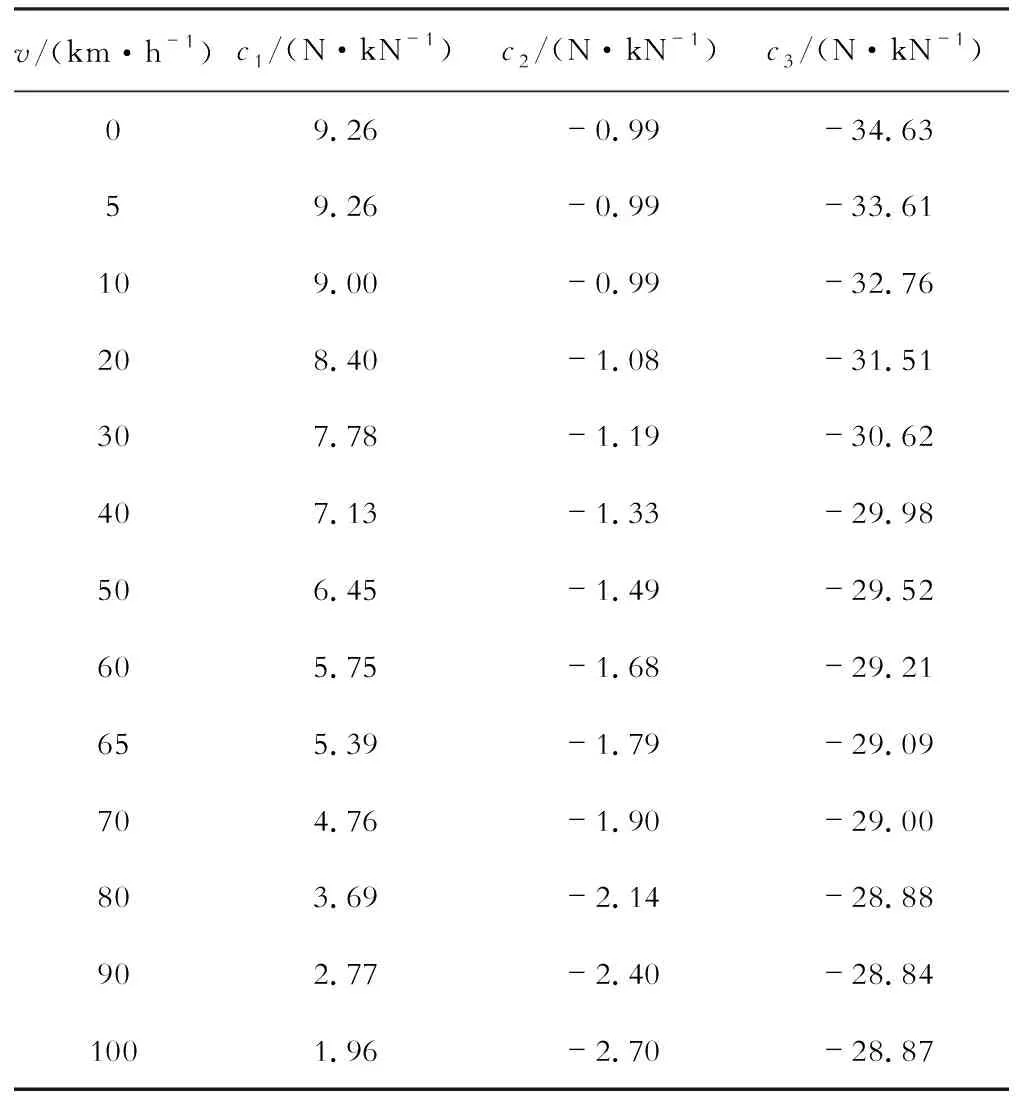
表1 列车单位合力计算结果Table 1 Calculation results of train unit resultant forces

为了更加直观地表示出列车运行速度与3种工况单位合力的关系,现绘制列车3种工况的合力v-c曲线,如图6所示.图中横坐标为速度,横轴的数值位置代表相应的坡段坡度,y正轴为上坡,y负轴为下坡,纵坐标为单位合力,各条曲线分别表示机车不同操纵状态.牵引工况时,合力为机车单位牵引力与列车单位基本阻力的差值;惰行工况时,合力仅为列车单位基本阻力;在实施空气制动时,合力为列车单位基本阻力与空气制动力之和;装有电阻制动或液力制动的机车,也能够绘出相应的制动力曲线.由图6可知,牵引工况与制动工况下的合力绝对值随速度提高而降低,惰行工况下的合力绝对值随速度提高而增加,且该种牵引质量条件下,HXD1C机车牵引的列车不宜在坡度为29‰及以上的长大坡段下坡运行,因为在该种长大坡段上实施制动时,随着速度的增加,列车单位合力会由负值逐渐变为正值,从而使列车加速,导致列车制动失效,对列车安全具有重要影响.同时,HXD1C机车牵引的列车应避免在超过坡度为9‰的坡段上坡运行时停车,否则会因为该坡段的起动阻力过大而导致列车无法起动.利用合力曲线可以求出列车在区间各种路段上的运行速度,列车在区间的往返行走时分,以及列车在下坡道上的限制速度和制动距离等.

图6 HXD1C型机车牵引5 520 t货物列车的单位合力曲线Fig.6 Unit resultant force curve of HXD1C locomotive pulling 5 520 t freight train

3.2 列车区间运行时分计算

计算所得的列车单位合力数据供电算列车区间运行时分时调用.本文设定列车以牵引工况通过A-B区间,根据A-B区间的线路纵断面,逐段输入每一个坡段的坡度和坡长,进而得到列车通过每一坡段的时间、运行距离、经过变坡点的速度等数据.根据该数据即可了解到列车的区间通过能力,并且制定出HXD1C机车运用管理策略,充分发挥HXD1C机车的牵引能力,同理,也可以得到其他HXD系列机车的运行数据.A-B区间第4坡段的电算结果如图7所示.经过统计,得出列车通过1～4号坡段的实际运行距离和时分,见表2.

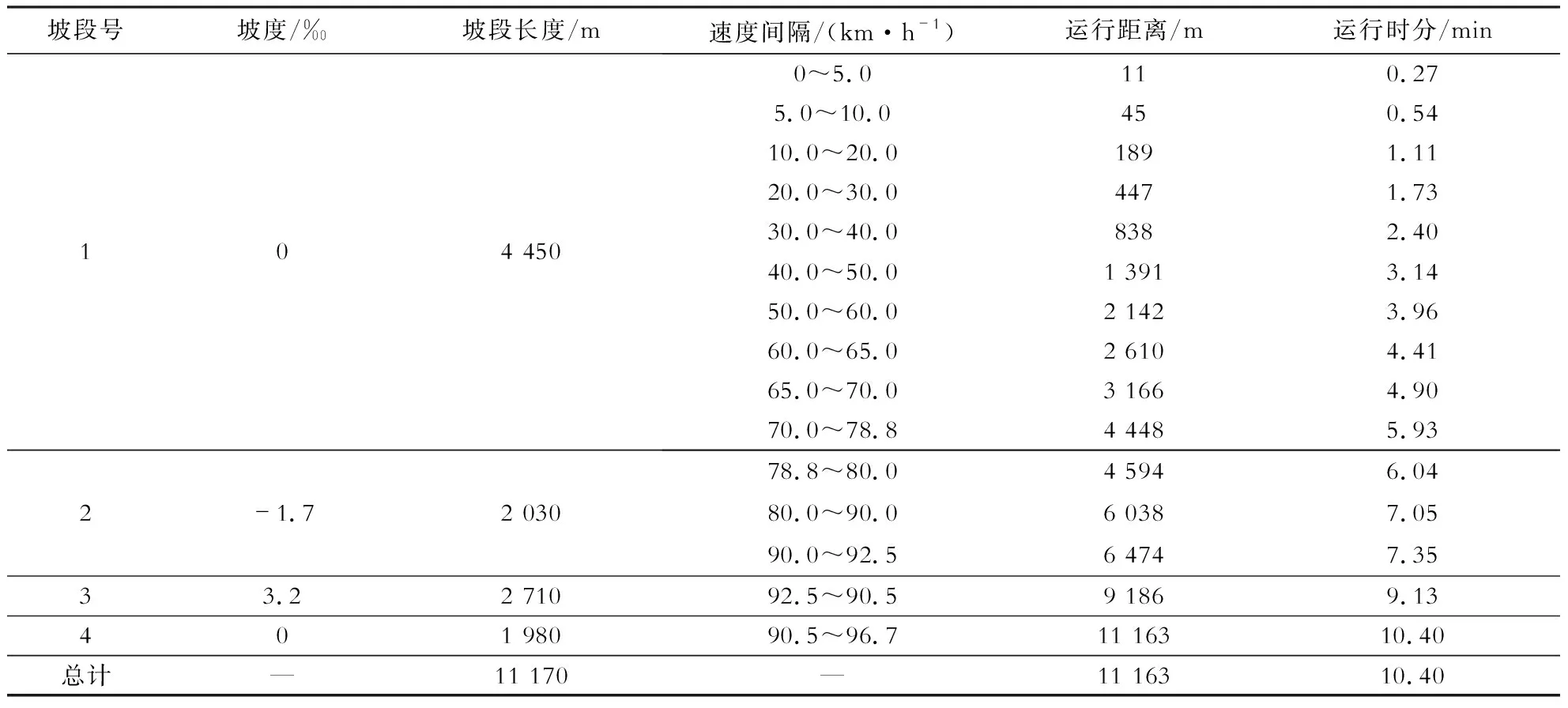
表2 A-B区间列车运行时分计算结果Table 2 Calculation results of train running time in A-B section

图7 第4坡段列车运行时分电算结果Fig.7 Computerized results of train operation time on the fourth slope section

由表2可知,列车通过1号坡段的运行距离与实际坡长误差为-2 m;2号坡段为-4 m;3号坡段为2 m;4号坡段为-3 m,1～4号坡段合计误差为-7 m,符合牵引电算系统设计中距离误差±10 m的要求.

4 结 语

为解决HXD系列机车在区间通过能力和运用管理等方面存在制约的问题,本文基于列车牵引计算基础理论,建立了HXD系列机车牵引计算模型,并利用VB 6.0软件编制了HXD系列机车牵引电算系统,有效完成HXD系列机车牵引列车区间运行时分的计算,同时符合电算系统设计的误差要求.下一步可以拓展HXD系列机车牵引电算系统的机车质量和机车能耗计算等功能,充分发挥HXD系列机车的运用能力.