概念设计中可重构航天器动特性快速预示方法

郭达维，贺媛媛，岳振江，康 杰，刘 莉

(北京理工大学宇航学院，北京 100081)

0 引 言

随着航天技术的不断发展和空间应用需求的拓展，在轨航天器系统组成及结构日益复杂，为保证航天器在外太空环境下长期稳定运行，并解决传统航天器任务响应时间长、部件重用率低等突出问题，面向在轨服务的可重构航天器设计理念应运而生。其将卫星的组件、子系统进行拆分，设计形成标准化模块，结合模块化即插即用技术与卫星平台技术[1]，这种具有标准接口、长期在轨运行的公用平台通过多次发射及在轨组装而形成[2-5]。得益于模块化以及面向在轨服务的设计思想，可重构航天器的设计灵活性、可维护性和可拓展性较传统航天器明显提高[6-8]。

在轨运行时，可重构模块可借助机械臂及标准对接装置实现移动和模块拼接组合[9]，形成各类模块组成、拼接方式不同的航天器构型。在概念设计阶段，设计人员具有较大的创新空间，需要结合设计对象特点形成的概念设计方法支持设计工作。McManus等[10]提出了考虑风险的方案选择和概念设计方法，该方法侧重于考虑航天器复杂系统设计风险的同时，将一系列不具有明确定义的需求在短时间内转化为较为详细的概念设计方案。Oxnevad等[11]为支持空间设备及太空望远镜的概念设计工作，开发了并行概念设计环境，集成了建模、光学分析、热设计与分析等功能，并能实现相关功能的数据传输，最终有效减少了概念设计阶段的耗时。郭达维等[12]针对可重构航天器需要考虑几何和性能双重约束的特点，提出了一种基于可视化模型的可重构航天器概念设计方法，可实现不同可重构航天器构型的设计与拼装。

整器基频及大部件刚度是航天器总体参数中的重要组成部分[13]，在可重构航天器概念设计中，需结合构型包括固有频率、模态振型在内的结构动特性判断设计方案的合理性。可重构航天器结构中由于预紧力的存在而产生接触、摩擦等局部非线性因素，工程上为实现对复杂结构航天器动特性的快速评估，采用子结构模态综合法以降低计算耗时、提高分析效率[14-15]，但对子结构进行模态综合时常将界面节点的关系设置为固连[16]。对于可重构航天器而言，每个模块适合划分为子结构，模态综合时直接将界面两侧固连的处理方法会使连接刚度偏高，进而导致固有频率偏高[17]。而对精细化模型进行动响应分析，再利用动特性辨识方法分析耗时较长，特别是当航天器构型复杂、自由度高时，所需的计算和时间成本无法满足概念设计的需求。此外，由于具有多个标准对接装置、预紧力大小可调以及模块化的特点，使得可重构航天器概念设计阶段需要对大量构型方案进行论证。

针对概念设计阶段可重构航天器动特性预示所存在的问题，本文提出了一种可重构航天器动特性快速预示方法。其中考虑了接触、摩擦等因素对于结构动特性的影响，方法流程中包括动特性分析与辨识、基于虚拟材料的模型等效和等效参数估计等步骤，对精细化模型实现了等效替代。经算例验证，该方法分析效率高，所得结果准确，可有效支持可重构航天器概念设计阶段的设计与评估。

1 典型可重构航天器特点及组成分析

工程应用中，可重构航天器一般属于小型航天器，可实现在轨组装、在轨更换以及应用功能拓展。可重构模块被运载体送至目标轨道后，机械臂能对若干模块完成移动、拼接等操作，组成的可重构航天器应能实现稳定可靠工作。结合航天器在轨装配的特点及已有的可重构航天器成熟设计方案[18-22]，本文总结出典型可重构航天器的结构和机械特点：

1)为易于运载体运输，并避免在轨装配过程对机械臂操作精度提出过高要求，可重构航天器模块外形紧凑，具有小型化的特点。

2)模块标准对接装置结构简单可靠，一般为镜面对称结构，具有简易安全性，对接装置锁紧过程快速高效，连接后能够满足模块间热传导的需求，装置解锁过程简单且易于实现。

3)标准对接装置施加的预紧力大小可在一定范围内调整，能够保证航天器之间的可靠紧密贴合，使得航天器构型结构一般可近似为线性结构。

4)考虑到对接装置对于航天器结构重量的影响，及其能量消耗对航天器系统的影响，预紧力大小在合理范围内选择，不宜过大。

典型可重构航天器的主要系统组成包括主承力结构、标准对接装置和内部设备。为了在模块外包络形状紧凑的前提下提供足够的强度和刚度，并能为航天器内部设备提供密闭的环境，典型可重构航天器采用箱板式承力结构，内部设备安装于承力结构内侧，并根据各模块具体功能不同而有所差异。

标准对接装置是可重构航天器实现在轨机械连接、联合飞行以及安全分离的基础[23]，典型可重构航天器采用合作目标轻小型对接装置方案，装置示意图如图1所示。

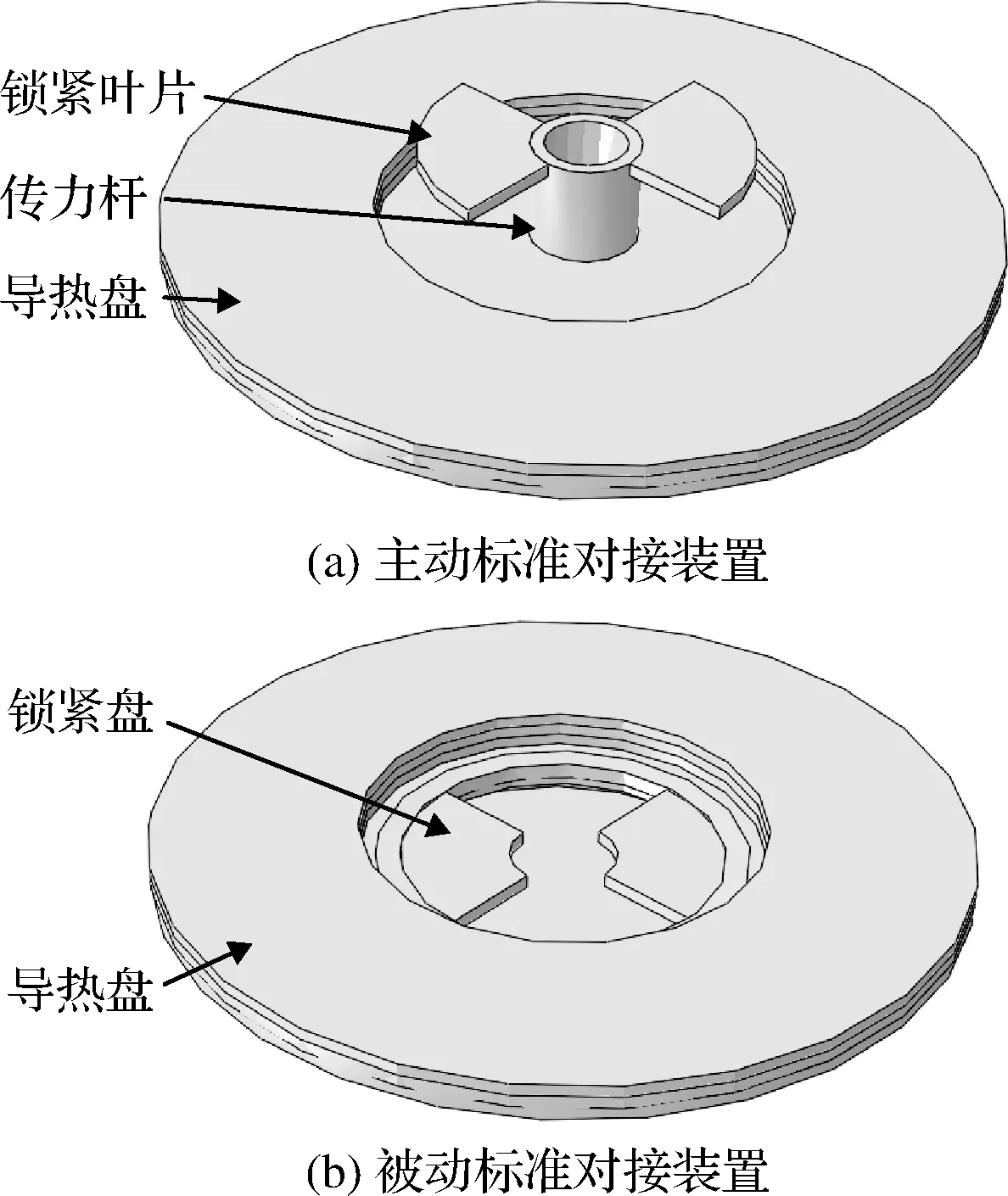
图1 对接装置示意图

标准对接装置可分为主动端及被动端，装置部件包括锁紧叶片、锁紧盘、传力杆以及导热盘等。为给模块电能和信息传输提供条件，传力杆为中空结构；导热盘包括底部支架与传热部件，用于传递不同模块之间的热量，在模块连接后导热盘将在预紧力作用下紧密贴合，支持航天器热控系统工作，实现航天器热平衡。

对接装置连接主要包括3个阶段：在外界操纵下模块逐渐接近，主动端装置锁紧叶片进入被动端装置内部；在电机等驱动装置作用下主动端传力杆旋转90°，使锁紧叶片和锁紧盘在连接方向上投影重叠，模块建立柔性连接；主动端传力杆根据预紧力大小设置在锁紧簧或电机驱动下向装置内部收缩，实现预紧力的施加，对接装置外侧圆环形导热盘贴合，完成对接装置的连接，锁紧前后对接装置如图2所示。

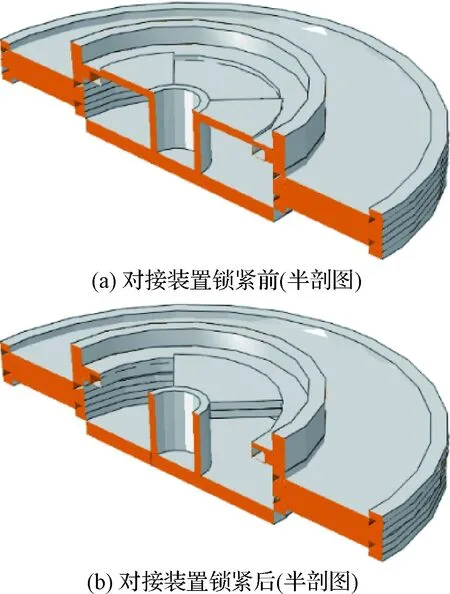
图2 对接装置锁紧示意图

标准对接装置中施加的预紧力使得导热盘之间、锁紧叶片与锁紧盘之间形成连接界面，且其中存在接触、摩擦等非线性因素。连接面的存在会对结构造成刚度损失，进而对固有频率、模态振型在内的结构动特性产生影响。

2 动特性快速预示方法

航天器概念设计作为工程中一个反复迭代、多轮逼近的过程，主要任务是将设计构思转化为对应的航天器构型方案，并通过分析快速做出方案的合理性判断。对于可重构航天器，特殊的构成形式赋予其更高的设计灵活性，使其较传统航天器而言，将形成更多概念设计方案，也就对构型特性预示的快速性提出了更高的要求。此外，标准对接装置的预紧力大小可在一定范围内调整，概念设计中也需要考虑预紧力变化对于可重构航天器构型结构动特性的影响。

本文面向概念设计需求，提出可重构航天器动特性快速预示方法，按顺序可分为3个主要步骤，依次为：动特性分析与辨识、基于虚拟材料的模型等效以及等效材料参数估计与动特性预示，流程如图3所示。该方法的输入为概念设计获得的多种构型设计方案，具体包括模块拼接关系和预紧力取值。已知输入条件后，根据是否已具有满足精度要求的代理模型，选择免去前2个步骤直接进行等效参数估计与动特性预示或进行包括3个步骤的完整方法流程。

2.1 动特性分析与辨识

为了在时间、计算成本允许的前提下了解非线性因素对于航天器结构的影响，需要给出对接装置预紧力取值，利用精细化有限元模型进行动特性分析与辨识。在考虑分析效率的前提下，一般选取由主动端和被动端模块组成的双模块航天器构型作为分析对象，对模型施加白噪声激励，采用隐式求解器进行动响应分析。结合激励数据与动响应分析输出的加速度数据可得结构的频响函数，随后可进行结构的动特性辨识。

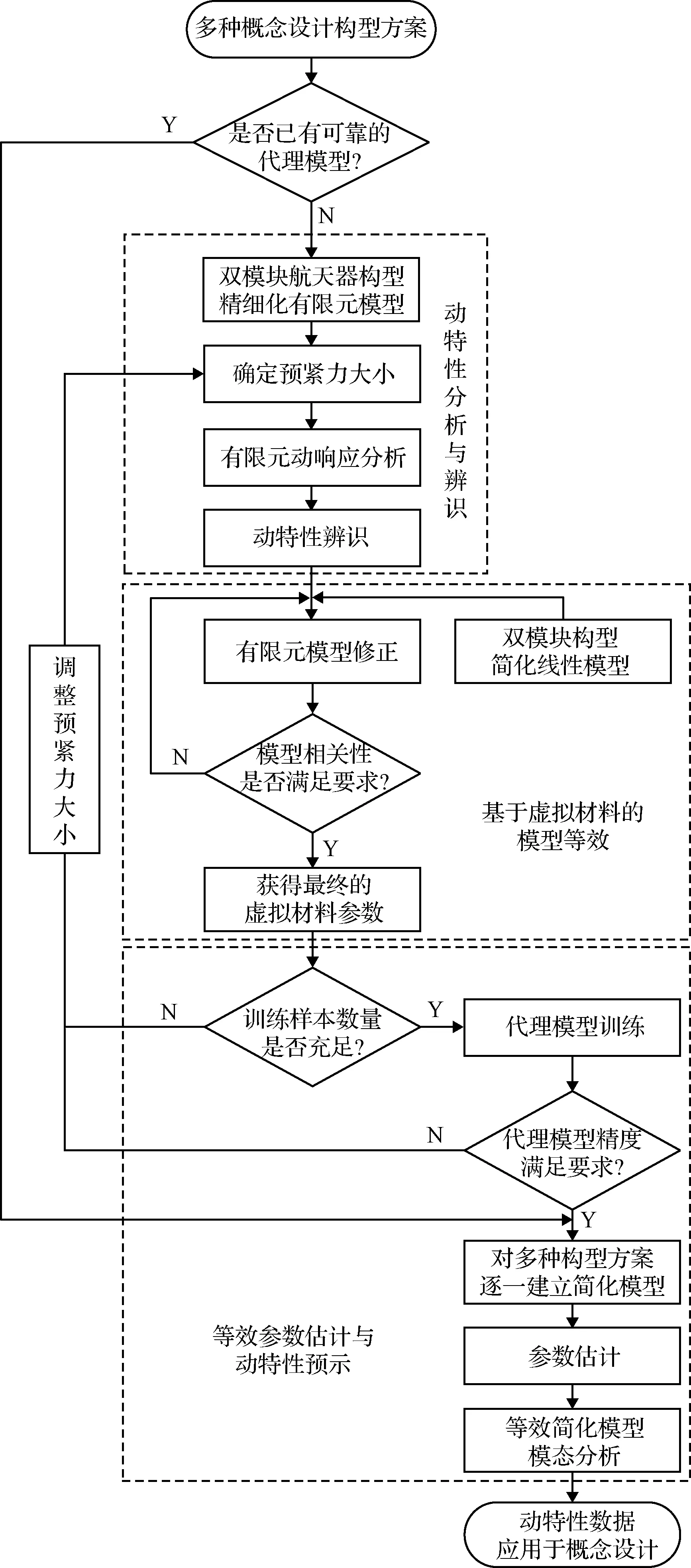
图3 快速预示方法流程

目前工程上大多基于结构线性化假设进行结构动特性辨识，应首先通过结构的线性化检测，确认分析对象模型能完成快速预示方法的后续步骤。目前常用的结构线性化检测方法包括：时域方法(时间序列检验、输出均值检验及平稳性检验等)；频域方法(Hilbert变换检验、频响函数检验及Lissajous检验)；幅值域方法等[24]，本文采用Hilbert变换(HI)检验方法，该方法的基本思想是线性结构频响函数H(ω)的实部服从于虚部的Hilbert变换，如式(1)所示：

Re(H(ω))=HI{Im(H(ω))}

(1)

经过线性化检测确认能近似为线性系统的结构，可基于线性化假设进行动特性辨识，获得包括固有频率、模态振型在内的结构动特性数据。

2.2 基于虚拟材料的模型等效

动特性快速预示的根本途径是在预紧力确定的前提下，使用简化模型代替复杂且计算成本高的精细化模型进行动特性预示。简化模型省略标准对接装置的细节特征，并将连接处的导热盘固连，可直接进行模态分析。

本文利用动特性数据，基于模型修正技术并引入虚拟材料，以完成精细化模型的等效，流程如图4所示。虚拟材料指的是以模型静、动力学特性为导向，在简化模型连接处设置的虚拟介质，模型修正中利用虚拟材料的材料属性参数实现对连接结构的等效模拟[25-26]。

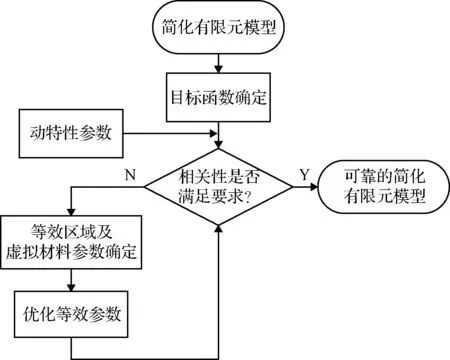
图4 模型等效流程图

对于模型修正问题，需确定修正目标函数、引入虚拟材料的等效区域和等效参数，可统称为模型修正前处理。本文根据动特性辨识所得数据，确定修正目标需考虑固有频率和模态置信准则(MAC，量符号记为M)，目标函数J(p)表达式为

(2)

式中：p=[p1,p2,p3,…,pb]T表示模型等效参数；k为考虑的模态阶数；wfreq,i及wshape,i分别为第i阶固有频率及模态振型对应的权重值；fsim,i(p)及fdyn,i(p)分别为简化模型及动特性辨识所得第i阶固有频率；Mi(p)为简化模型振型与动特性辨识振型的第i阶MAC值，表达式为

(3)

式中：φdyn,i及φsim,j分别为动特性辨识所得第i阶振型及简化模型第i阶的振型。

为保证模型等效的能力与效率，通过灵敏度分析等量化分析方法，先后选取对结构固有特性影响显著的等效区域与参数。首先根据工程经验初选在物理上存在疑问且与模型特征相关的区域[27]，再分别对备选区域材料弹性模量按比例上下浮动，对结构固有特性特征量进行比较，选取对特征量影响更明显的区域。

对于结构第i阶模态，关注的特征量为ai，则对应的归一化等效区域影响系数Di表达式为

(4)

通过对比备选区域的影响系数，可确定模型等效区域。等效参数一般为材料属性参数等，利用灵敏度分析实现选取，设简化有限元模型备选等效参数为p且共有n个量，特征量c为等效参数的隐函数。当p发生小扰动时，第i阶特征向量ci有一阶泰勒展开式[28]，并可进一步改写为矩阵形式

(5)

SΔp=Δc

(6)

式中：Δp为备选等效参数改变量，Δp=[Δp1,Δp2,…,Δpn]T；Δc为特征量改变值，Δc=ci(p+Δp)-ci(p)；S为灵敏度矩阵，其表达式为

(7)

式中：m为特征量个数；c一般取为结构的固有频率及MAC值，也可根据模型等效的具体需求调整。

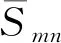
(8)

式中：Δqn为修正参数变化的比例。

通过上述灵敏度分析，确定对特征量影响显著的参数，即完成模型修正前处理。将有限元模型修正问题表述为式(9)所示的标准优化数学模型。可采用遗传算法(GA)等优化算法求解，得到简化模型虚拟材料区域的等效参数，完成对精细化模型的等效模拟。

(9)

式中：pj_min和pj_max分别为第j个等效参数的下界和上界。

2.3 等效参数估计与动特性预示

为在概念设计中对模块组成形式、对接装置预紧力确定的新构型方案实现动特性快速预示。基于动特性辨识结果，对不同预紧力情况的航天器构型进行模型等效，依据适合所选代理模型特点的试验设计方法，获得一定数量数据后，即可构建代理模型以实现等效参数估计。根据可重构航天器动特性快速预示方法的需求，代理模型输入为预紧力的取值，输出为等效模型的虚拟材料参数值。代理模型构建与交叉验证的流程如图5所示。

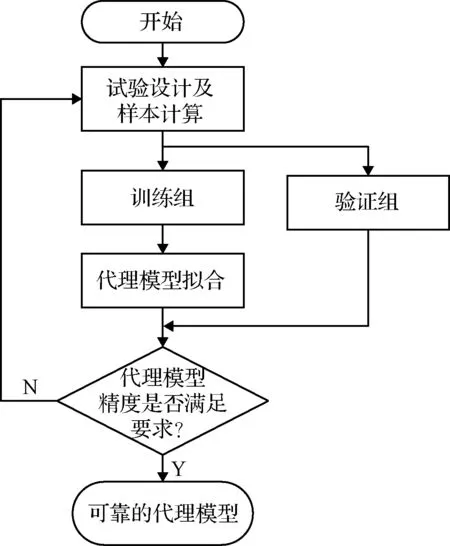
图5 代理模型构建及验证流程

获得满足要求的代理模型后，由于可重构航天器中存在非线性因素的对接装置结构形式统一，使用已有的代理模型，对输入的多种构型方案简化模型等效参数分别做出估计。形成的等效简化模型可通过有限元模态分析获得动特性数据，无需再进行动特性分析与辨识及基于虚拟材料的模型等效。在待分析构型方案众多的概念设计阶段，特性分析耗时将对设计进度产生重要影响。利用本文方法能高效实现航天器动特性的预示，为设计迭代工作提供效率保障。

3 仿真校验

3.1 典型可重构航天器建模

对典型可重构航天器模块进行有限元建模，航天器模块的承力结构和外壳材料均采用2A12铝合金，对接装置底部支架材料选用Ti-TC4钛合金，传热部件材料为铜合金，其余材料均为2A12铝合金，具体材料参数如表1所示。

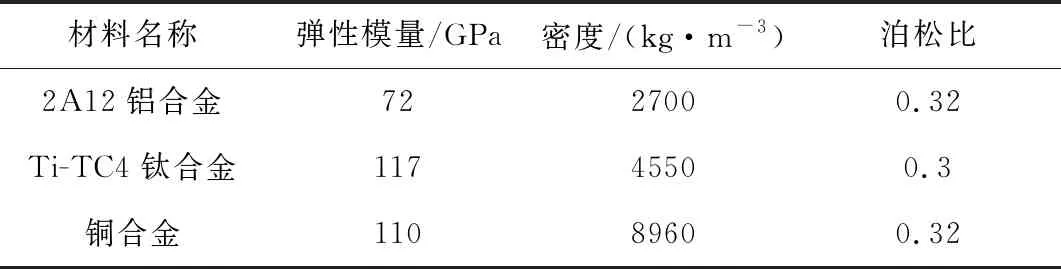
表1 可重构航天器材料参数Table 1 Material property of reconfigurable spacecraft

图6 可重构航天器有限元模型

模块内部其他有效载荷以等效非结构质量的形式分布在对应结构上，使用四节点减缩积分壳单元进行建模，得到的模型如图6所示。单个模块总重约为35 kg，外包络形状近似于边长为427 mm的正方体。根据对接装置类型，可分为左侧的被动端模块和右侧的主动端模块。

本文在考虑模块尺寸及重量的前提下，参考国内外同类航天器对接装置预紧力设计[18,30]，确定预紧力范围为250 N～1200 N。为研究不同预紧力下的航天器构型动特性，需将预紧力在一定范围内变化。以温度载荷法为等效手段施加预紧力[31]，将温度梯度载荷加载于主动端对接装置传力杆上，传力杆形变引起锁紧叶片、锁紧盘和导热盘间的接触挤压，所产生预紧力FT与温度载荷ΔT之间的关系为

(10)

式中：E为锁紧叶片、锁紧盘材料弹性模量；d，D分别为锁紧叶片、锁紧盘的内径和外径；α为传力杆材料热膨胀系数。

3.2 动特性预示

根据本文提出的可重构航天器动特性快速预示方法，利用双模块航天器构型获取非线性因素对于结构的影响，进行动特性分析与辨识。对预紧力取最小值时的航天器构型进行线性化检测，结果如图7所示。构型频响函数实部与虚部的Hilbert变换吻合，特别是在峰值点的吻合程度较高，说明对接装置预紧力为保证航天器间的紧密可靠连接，使得航天器构型中局部存在的接触、摩擦因素对整体结构影响有限，该结构能近似为线性系统，可基于线性化假设进行动特性辨识。

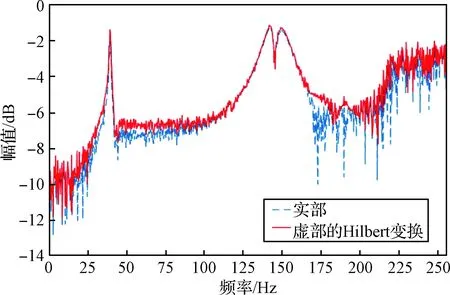
图7 结构线性化检测结果

利用PolyMax方法[32]对系统动特性参数进行辨识，以对接装置预紧力取600 N为例，获得结构动特性参数如表2所示，双模块航天器构型为对称结构，故其存在频率相同、振型方向不同的弯曲模态。

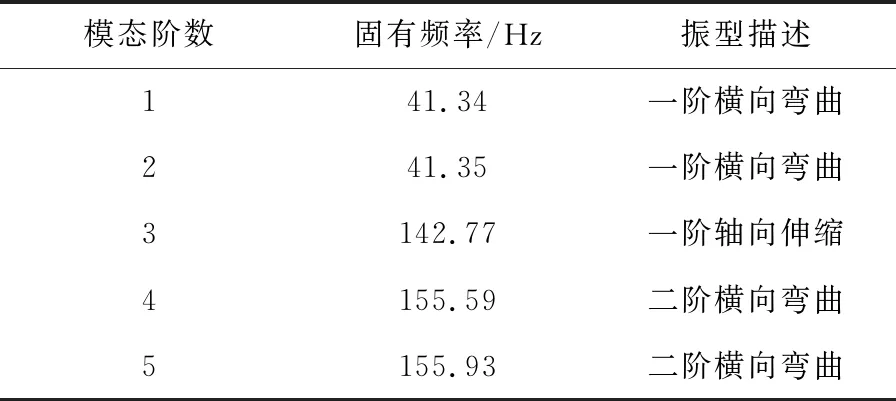
表2 辨识获得的结构动特性参数Table 2 Identification result of structural dynamic characteristics

本文建立的双模块航天器构型简化模型如图8所示。以工程经验初选模型等效区域，再结合灵敏度分析方法，确定等效区域为简化模型连接导热盘处的环状区域。为保证模型等效的效率，将等效区域平均划分为4个等效参数独立的子区域，其虚拟材料设置为二维各向异性材料。以固有频率和MAC值为特征量，通过灵敏度分析选取材料属性矩阵中的3个对角元素为等效参数，等效参数共计12个。

以预紧力取600 N的构型为例，利用遗传算法，对所建立的构型简化模型基于虚拟材料进行模型等效，以精细化模型辨识结果为参考，等效处理前后简化模型固有频率误差、MAC对比如表3所示。

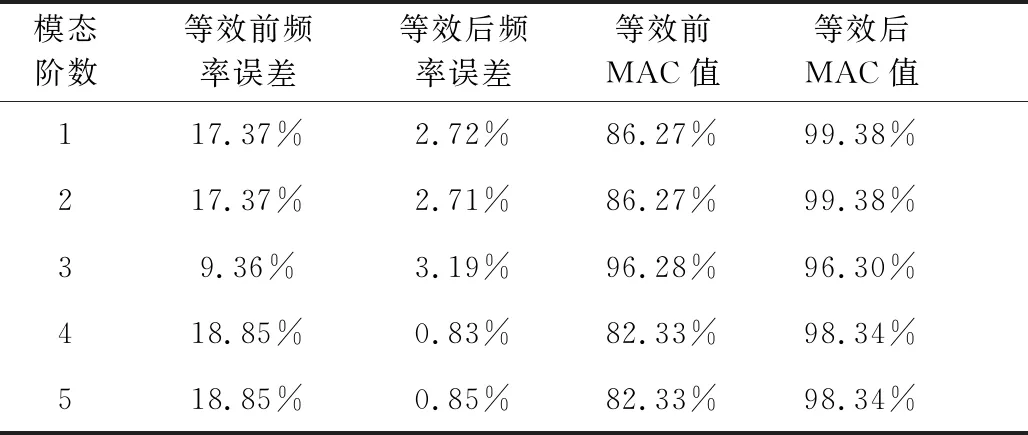
表3 模型结构动特性误差对比Table 3 Structural dynamic characteristics comparison of models

从表3可以看出，等效处理后的简化模型精度满足工程中固有频率误差小于5%，MAC值大于90%的标准[33]，实现了精细化模型的等效。

基于动特性快速预示方法流程，在对接装置预紧力取值范围内形成一定训练样本并构建代理模型。选用Kriging代理模型，其为针对空间分布数据的无偏最优估计插值模型[34]，采样方法为拉丁超方设计方法(LHD)，通过精度验证其相对均方根误差(RMSE)均在3%以下，满足工程应用要求。

结合文献[6]中对于可重构航天器的设计思想，本文设计形成如图9所示的构型方案，该构型可用于通信、遥感等空间任务，可重构航天器所具有的在轨组装、模块化等特点降低了对于运载体的尺寸要求，提高了航天器的任务灵活性。

图9 构型方案示意图

以构型方案预紧力大小取450 N为例，获得结构动特性数据的方法包括三种：本文提出的动特性快速预示方法、将模块连接处固连且不进行等效处理的简化模型模态分析、使用构型精细化模型的动响应分析及动特性辨识。上述三种方法所得动特性数据对比如表4所示。

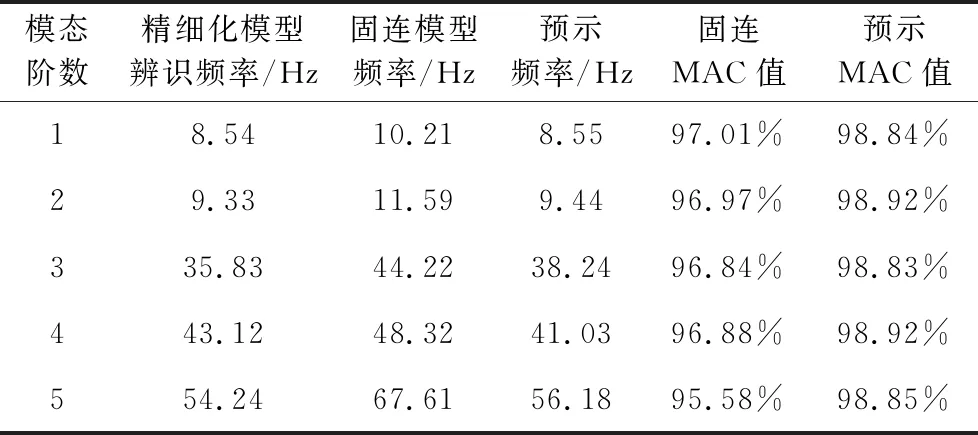
表4 结构动特性结果对比Table 4 Comparison of structural dynamic characteristics result

上述方法中最后一种基于精细化有限元模型进行分析，动响应分析过程极其耗时，在需要对大量构型方案快速评估的概念设计阶段，该方法将大幅提高概念设计在整个工程任务中的耗时占比，显然不利于发挥可重构航天器设计灵活、面向任务快速拓展等优势。以该方法结果作为标准参考，与其他两种方法计算MAC并进行对比。由表4可知，固连模型与精细化模型所得结果差异较大，无法正确反映出航天器构型的结构动特性。本文提出的动特性快速预示方法单次求解耗时约为70 s，在分析效率高于精细化模型的同时，所得动特性结果准确，能够满足工程上对于构型动特性评估的要求。

4 结 论

针对可重构航天器特点及概念设计方法对结构动特性预示的需求，本文通过动特性分析与辨识、基于虚拟材料的模型等效和等效参数估计形成了预示方法流程。仿真校验表明，该方法能对构型动特性进行准确预示，结果精度符合工程要求。此外，快速预示方法充分考虑可重构航天器概念设计阶段构型方案众多、设计参数含预紧力等特点，有效兼顾了分析的效率与准确性，提供了构型方案特性分析、设计迭代和优化的实现基础。