圆形太阳翼模态仿真与试验研究

吴志培，刘志超，荣吉利，吴跃民，辛鹏飞,5，罗 强

(1.北京理工大学宇航学院，北京 100081；2.中国运载火箭技术研究院, 北京 100076；3.空间物理重点实验室，北京 100076；4.北京空间飞行器总体设计部，北京 100094；5.北京空间飞行器总体设计部，空间智能机器人系统技术与应用北京市重点实验室，北京 100094)

0 引 言

圆形太阳翼是在航天器轻质化及大收纳比的新需求下发展起来的一种新型柔性太阳翼，是一种典型可展开薄膜空间结构；最早于20世纪90年代由美国ATK公司提出，具有重量轻、收拢体积小、展开刚度高、可扩展性强等优点，并已广泛应用于国外的航天器中[1]。由于圆形太阳翼低阶固有频率通常较低，其展开锁定后容易受到太空环境的激励而造成大范围运动，这种运动轻则影响航天器姿态，重则使结构发生破坏。为了避免结构固有频率与外界激励频率相近而造成不可挽回的损失，在实际应用前，通常会对圆形太阳翼进行地面模态试验。然而试验时，结构的模态容易受到重力、重力卸载系统及其他外在载荷环境的影响。因此，对展开锁定状态下圆形薄膜太阳翼的精确模态计算及试验研究是十分有必要且迫切的。

目前，国内针对圆形太阳翼等大面积薄膜结构的计算及试验研究起步较晚。文献[2]剖析了空间太阳能电池阵列包括结构设计、展开机构技术等关键性问题，阵列模型涉及体装式、多板展开式以及柔性展开式等；文献[3-4]均针对充气式薄膜空间结构的展开动力学进行了软件仿真分析；文献[5]以平面薄膜天线为研究对象，通过有限元软件仿真与等效模型解析解相互印证，对系统进行了优化设计及模态分析；三篇文献均对典型的空间薄膜结构进行了研究，但并未以圆形太阳电池阵为研究对象展开相关技术研究分析，包括模态试验及模态灵敏度仿真分析等。在圆形太阳翼研究方面，文献[6]针对UltraFlex太阳翼，利用SAMCEF有限元软件对其展开过程进行动力学仿真分析与模态分析，研究了不同转角驱动函数对其展开稳定性的影响和悬吊卸载系统下的SAMCEF数值模型的准确性和有效性；然而并未对悬吊系统乃至其他影响模态的因素进行较深层次的分析，且文中未提及模态试验内容。文献[7]基于绝对坐标方法建立了刚柔耦合UltraFlex太阳翼动力学模型，完成系统展开稳定性研究，但不涉及模态仿真及试验研究。在圆形太阳翼的试验方面，文献[8]仅针对太阳翼的基板进行了模态仿真分析和试验验证。完整圆形太阳翼的模态仿真分析与试验研究，国内尚缺少此方面的公开文献发表。

国外对圆形太阳翼有关研究起步较早，并多次成功进行了模态计算以及试验研究。针对UltraFlex-175圆形太阳翼模型，NASA及ATK公司首先利用有限元软件ANSYS进行了模态仿真分析，再利用单点激振方式，布置十五个加速度传感器进行数据采集，采用刚性弹簧悬吊太阳翼，对半径为2.55 m的高仿真度圆形太阳翼在真空环境和空气压力环境下进行模态测试，并分析了空气对太阳翼模态的影响[9-11]。然而，其模态试验采用的刚性弹簧及加速度传感器会带来附加质量和刚度的影响，影响了整体模态精度；虽然加速度传感器在理论上能获得更高精度的模态数据，但也因此导致试验布置的测点较少。同时，由于柔性太阳翼的模态密集，试验采用单点激振不容易激起整体模态，导致进行模态辨识时，容易发生模态遗漏。此外，根据NASA已有研究报告，其针对太阳翼模态试验前的模态敏感度分析工作并未展开。综合而言，NASA针对圆形太阳翼的模态试验方案在精度上存在不足，具有可优化的空间。此外，传统的试验模态分析方法建立在系统输入输出数据均已知的基础上，然而由于实际输入信息获取较难，这些方法具体应用存在局限性。采用双点激励和工作模态分析技术[12]可以避免模态遗漏和对输入信息的采集，有效提高测试精度及效率。

在此背景下，本文首先利用有限元软件SAMC-EF对圆形太阳翼进行模态敏感度仿真分析，探究翼面预紧力、约束方式、重力及重力卸载系统等因素对圆形太阳翼模态的影响，求得模拟地面试验状态的圆形薄膜太阳翼的前四阶模态，据此确定模态试验的初始状态，包括约束、悬吊系统等。随后，采用工作模态法，根据确定的模态试验实施方案进行试验布置。测振方式采用激光扫描手段，可布置较多测点。紧接着经验证测试、预试验及正弦扫频试验，对圆形太阳翼的前四阶模态进行测试。最后，根据测试结果对SAMCEF有限元模型进行修正，提高了模型精度。

1 太阳翼模态敏感度仿真分析

利用SAMCEF有限元软件对圆形太阳翼进行数值仿真分析，可与地面模态试验相互印证，提高试验的效率和数据的可靠性并形成理论模型用于指导类似模型的研究。在SAMCEF软件中，翼面所选模拟单元为Membrane单元，无面外刚度。因此首先需要对翼面进行预紧，并对太阳翼进行静力学分析，得到系统质量矩阵和刚度矩阵用于后续的模态分析。太阳翼模态敏感度分析变量主要包括翼面预紧力、约束方式、重力及重力卸载系统等，并可由此确定圆形太阳翼进行模态试验时的试验状态。

1.1 有限元模型

以北京空间飞行器总体设计部研制的一种新型柔性太阳翼为参考模型，有限元模型主要由箱板、碳纤维肋条、太阳毯组成。圆形太阳翼三种有限元模型如图1，图2和图3所示，各结构部件材料参数见

图1 不含支撑车模型

表1。为更加真实模拟实际应用，表1中太阳翼的主要结构，即肋条与翼面，由碳纤维材料和聚酰亚胺膜组成，其弹性模量经过多组试验测试所得。

图2 含支撑车模型

图3 含卸载弹簧模型

表1 圆形太阳翼的材料参数Table 1 Material parameters of Circular Solar Arrays

表2 不同温度载荷作用下太阳翼的前六阶固有频率Table 2 The first six natural frequency of solar arrays under different temperature loads

1.2 翼面预紧力对模态的影响

试验过程中一般以太阳翼面中部的下移量为标准衡量其翼面预紧力。为探究翼面预紧力对太阳翼模态的影响，依次对连接绳施加4组温度载荷，测得太阳翼前六阶固有频率如表2所示。可见，太阳翼前两阶模态对预紧力变化不敏感，且随预紧力增大有减小的趋势；而第4至6阶，模态频率随预紧力增大而增大并在第四阶模态频率上，差值达到10.36%。综合而言，预紧力变化对太阳翼模态的影响程度较大；因而在测试翼片中部下移量时应当足够精确，并且进行数值分析时，得到的静力学状态应当尽量接近实际的试验状态。

1.3 约束方式对模态的影响

圆形太阳翼实际在轨工作状态下，其静止箱板根部通常与航天器相连。由于航天器质量较大，因此可以近似将太阳翼静止箱板根部固支。在地面试验时，常在太阳翼下方安装支撑车以保护太阳翼，但支撑车底座依靠车轮制动，在地面有轻微滑动的风险。此外，支撑车与太阳翼相连的螺栓自身刚度较小且存在连接间隙，此类因素会降低连接刚度进而影响模态分析。为确定试验过程中的太阳翼的约束方式，探究支撑车对圆形太阳翼模态的影响是有必要的。

针对此类状况，设计三种约束方式，分别为有支撑车底座固支、有支撑车底座面内弹簧约束和无支撑车箱板根部固支。不同约束方式下圆形太阳翼的模态频率如表3所示，多种支撑车约束方式均主要影响太阳翼的第一阶模态频率；有支撑车相比无支撑车，第一阶频率差值较大，达到32.89%。而无支撑车的固支方式最接近太阳翼真实应用的约束状态，因此进行地面模态试验时，采用支撑车不能满足要求。

表3 不同约束条件下太阳翼前六阶固有频率Table 3 The first six natural frequency of solar arrays under different constraints

1.4 悬吊弹簧对模态的影响

圆形太阳翼地面模态试验时，为模拟失重环境，通常选用悬吊弹簧作为重力卸载装置并起到保护太阳翼的作用。然而，悬吊弹簧作为附加结构会影响结构的模态。因此，在试验前研究悬吊弹簧对模态的影响十分有必要。参考NASA的UltraFlex-175太阳翼模型，利用SAMCEF软件可对含重力卸载弹簧的圆形太阳翼进行限元建模。文献[6]给出了含悬吊弹簧的圆形太阳翼模态仿真分析结果，并与NASA的ANSYS仿真结果和地面试验结果进行对比；相关误差符合美国TRL6的相关技术标准，证明了含有悬吊弹簧重力卸载系统的圆形薄膜太阳翼有限元模型的准确性和有效性。本节在此基础上，进一步进行了重力场及悬吊弹簧重力卸载系统对太阳翼模态影响的研究。

1.4.1重力场及悬吊弹簧对模态的影响

地面试验时，地面重力场会使太阳翼面下垂并改变太阳翼面预紧力进而影响模态。通过有限元软件SAMCEF对圆形太阳翼进行仿真分析得到重力场及悬吊重力卸载弹簧对圆形太阳翼前六阶模态的影响如表4所示。由此可知，重力作用使太阳翼第1阶模态频率减小，使第2至6阶频率增大；悬吊弹簧的作用则相反，增大了第1阶固有频率，而第2至6阶减小。参考翼面预紧力的影响，重力作用与翼面预紧力作用趋势一致，第一阶降低而大体上呈上升趋势；此外，以无重力环境为对比，由差值百分比发现，重力卸载弹簧可以减轻重力场给系统模态带来的影响。图4为重力场及悬吊重力卸载弹簧同时作用下，模仿圆形太阳翼地面试验所得前四阶模态振型。

1.4.2悬吊弹簧刚度对模态的影响

通过改变重力卸载弹簧的刚度，探究弹簧刚度对于太阳翼模态的影响，弹簧刚度不同时太阳翼的前六阶固有频率如表5所示。由此可知，随弹簧刚度的增大，太阳翼的频率波动变化，且不够明显。对于太阳翼的前四阶模态，当弹簧刚度在7 N/m之内时，刚度的变化导致的模态频率差值在0.59‰之内，可以忽略不计。

表4 有无重力场作用下太阳翼前六阶固有频率Table 4 The first six natural frequency of solar arrayswith or without gravity

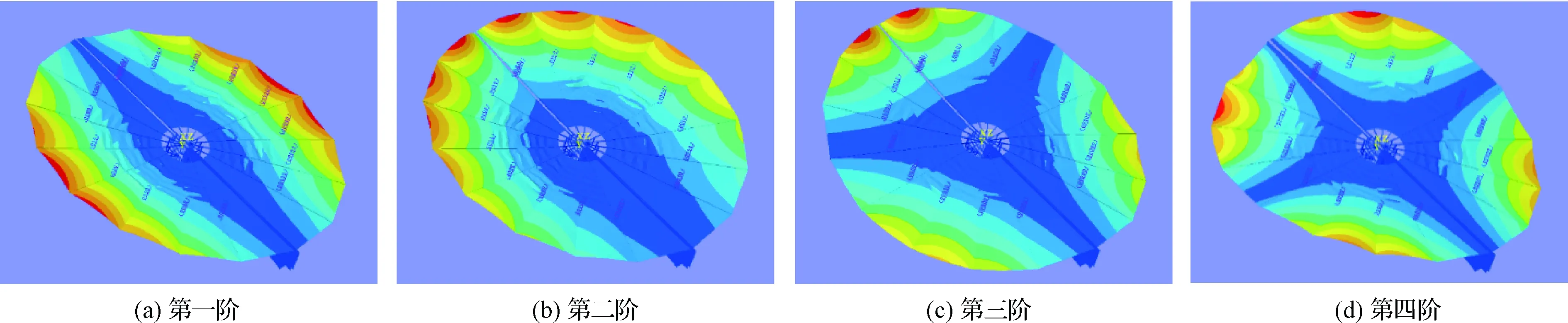
图4 悬吊弹簧作用下太阳翼前四阶模态振型

表5 重力卸载弹簧刚度不同时太阳翼前六阶固有频率Table 5 The first six natural frequency of solar arrays with different suspension spring rigidities

2 太阳翼模态测试试验

根据SAMCEF数值分析的结果，确定了圆形太阳翼模态测试的约束方式，重力卸载系统的选取等关键问题。本次测试基于工作模态法，利用两个激振器同时激振，利用激光扫描测振仪自动采集工作状态的响应，采用正弦扫频测试从而获得圆形太阳翼的前四阶模态振型与固有频率。

2.1 工作模态分析原理

工作模态分析亦常称为环境激励下的模态分析，其优点在于仅需测试振动响应数据，由于这些数据直接来源于结构实际所经受的振动工作环境，因而识别结果更符合实际情况和边界条件，且无需对输入激励进行测试，节省了测试费用。

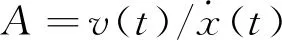
由PSV软件经过快速傅里叶变换得到如下频响函数：

H(ω)=A(ω)exp(jφ(ω))=P(ω)+jQ(ω)

(1)

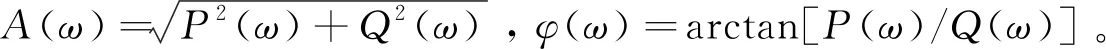
PSV软件处理数据得到的频响函数曲线中，峰值处横坐标即为系统的固有频率，峰值处纵坐标即为归一化后的响应幅值。

2.2 试验件约束与重力卸载系统

根据商业有限元软件SAMCEF数值仿真的结果，柔性太阳翼进行模态测试时的约束状态为静止板根部固支约束。为了实现这种固支约束，应将太阳翼静止箱板的根部与地面固连，由此需要设计与地面连接的夹持装置，夹持装置的设计示意图如图5所示。同时，选用外径为7 mm，内径为5 mm的硅胶管作为重力卸载系统。每根悬吊硅胶管的刚度仅为3.17 N/m；其值小于7 N/m，对系统刚度及模态分析的影响可忽略不计。图6为圆形薄膜太阳翼试验悬吊点分布示意图。

2.3 测振点与测振仪分布

根据有限元软件SAMCEF数值分析结果，测点在1.2 m之外分布密集，之内稀疏，为精确测得圆形太阳翼的模态振型，并提高测试效率，每一根肋条布置6个测点，肋条之间薄膜布置4个测点，图7给出了单片翼片上测点的位置布置示意图，其他翼片上按照同样的布置方式。

利用PSV-400扫描式激光测振仪对圆形太阳翼模态数据进行采集。PSV-400激光扫描仪的扫描角度为40°，因此需要确定激光扫描仪的悬吊高度H，如图8所示，其中激光扫描测振仪的镜头需正对太阳翼的中心，并且满足扫频视角包含整个太阳翼。由图可知H=R/tan(20°)=5.49 m，因此，激光扫描测振仪的镜头必须在太阳翼中心机构正上方5.49 m以上。

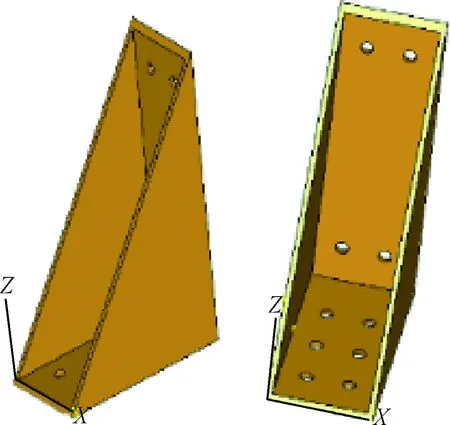
图5 夹持装置

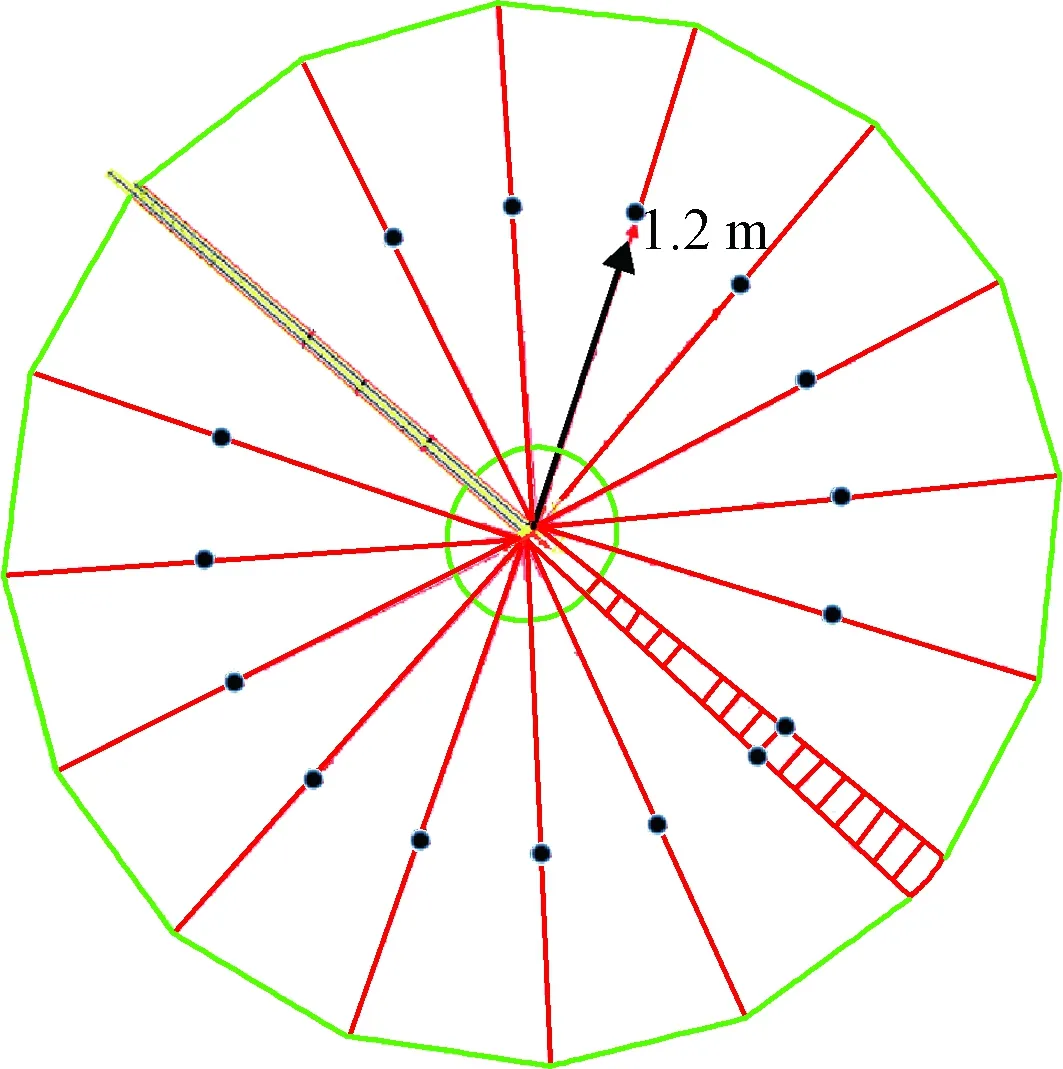
图6 太阳翼悬吊点位置

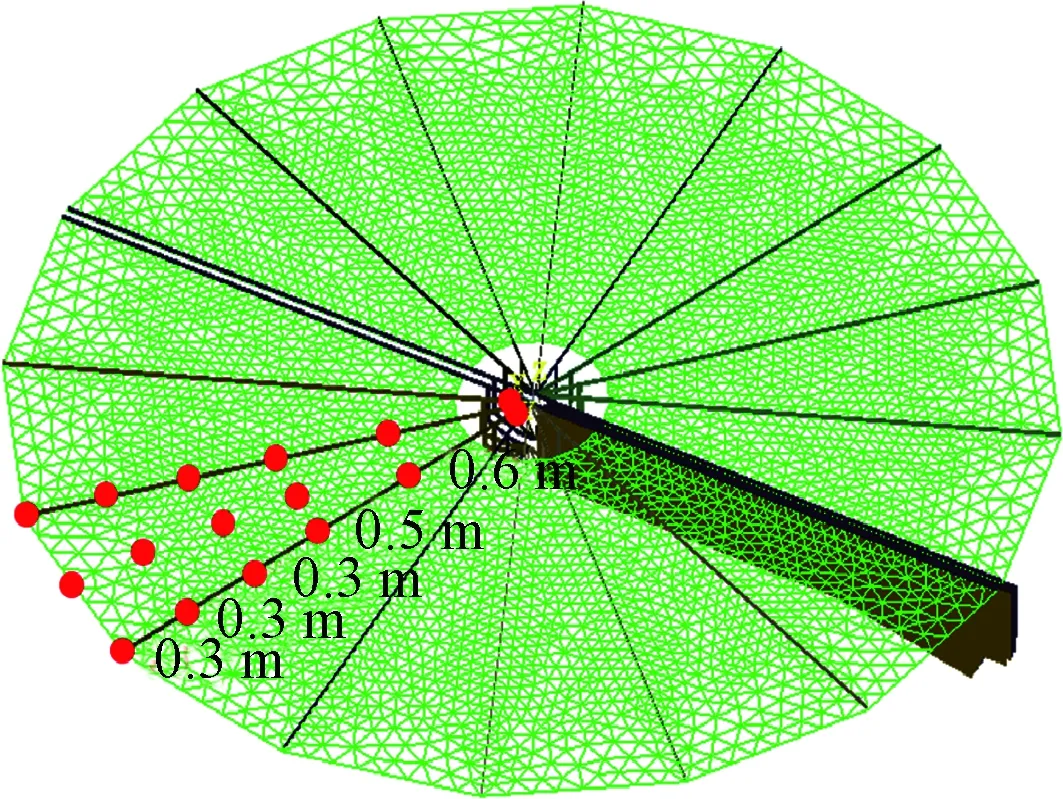
图7 单翼测点位置

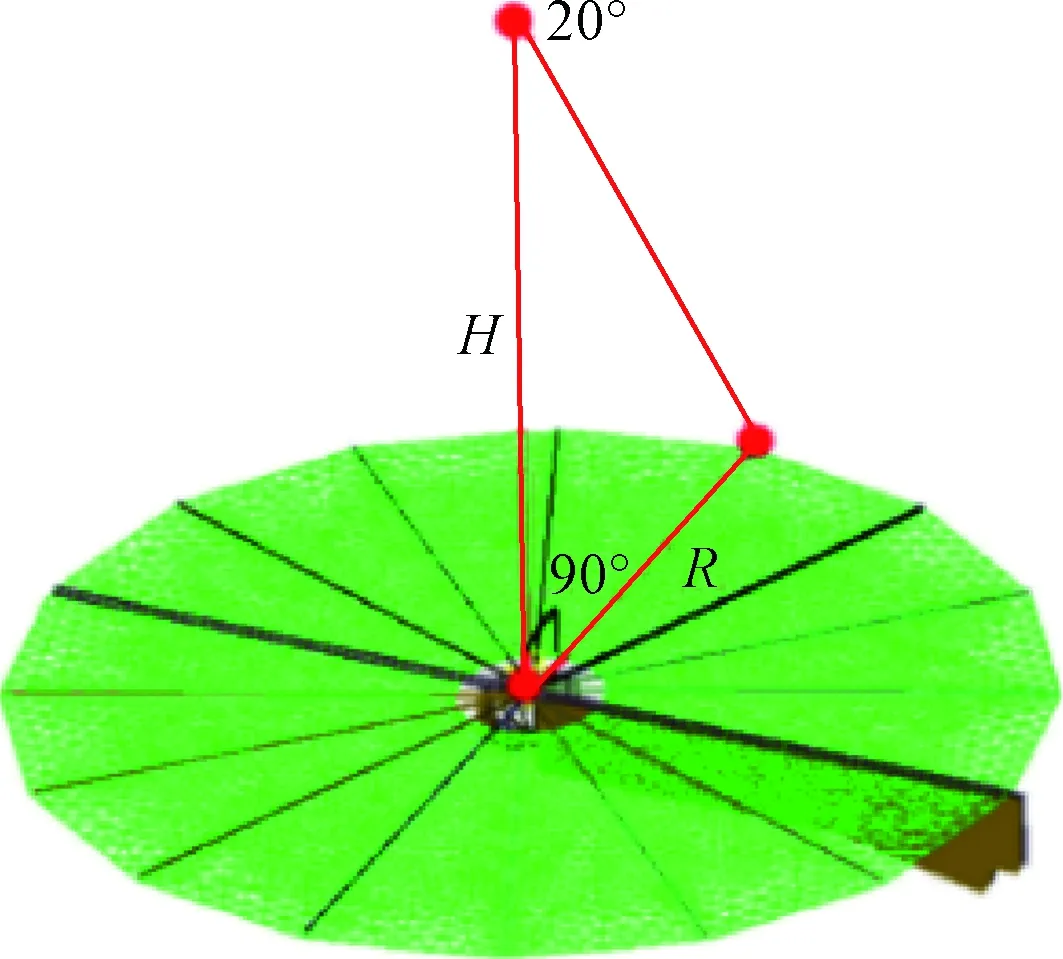
图8 测振仪安装高度

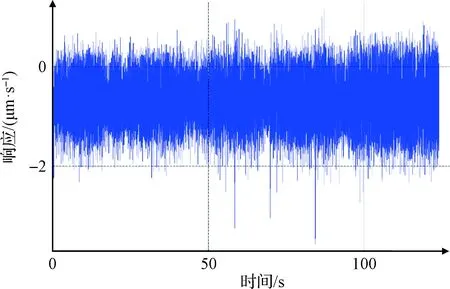
图9 太阳翼静止板根部响应

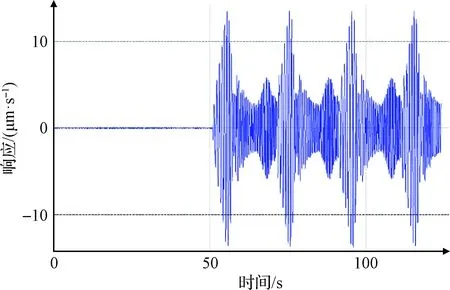
图10 太阳翼翼面响应

2.4 固支约束测试验证

根据SAMCEF分析结果可知，太阳翼静止板根部固定，更加能够模拟太阳翼实际工作的工作状态，对于固支约束的验证是进行后续试验的前提和基础。对太阳翼进行激振时，利用单点激光测振仪测量静止板根部的响应，并与太阳翼面的响应数据对比。测试过程中，前50 s激振器不工作，50 s以后激振器开始激振，太阳翼静止板根部的响应数据如图9所示，太阳翼翼面的响应数据如图10所示。

由图示可知，激振过程中，太阳翼静止板一直有噪声信号却无激振信号，最大速度幅值为3 μm/s；而太阳翼翼面前50 s只有噪声信号，开始激振后，翼面响应最大值为11 mm/s，响应结果相差三个数量级，因此验证了固支边界的有效性。

2.5 正弦扫频测试

首先进行多次预实验优化试验模型。参考预试验结果，为准确识别模态参数、提高测试精度及防止模态遗漏，采用激振器输入为参考信号和两点对称激励的方式。同时，为防止激振器的附加约束作用影响太阳翼的模态振型，将关于箱板对称的两个激振器布置于太阳翼肋条根部，并将激振器的电压幅值降至0.15 V以保护太阳翼。正式测试时，测点共167个；先进行粗扫描，单点扫描时间为16 s，确定太阳翼模态振型的合理性；随后，缩小扫描频率范围，使用更细的扫描分辨率进行精扫描，单点扫描时间为128 s，以获得更精确的太阳翼模态。

利用扫频法进行模态测试时，根据预试验模态测试结果，设计了三种不同工况，如表6所示。每种工况先进行粗扫描再进行精扫描，所对应肋条位置由图11给出。奇数编号的粗扫描，以有限元数值仿真结果作为参考，由试验结果发现Scan1和Scan3分别激发的第二和第三阶模态振型与数值仿真结果基本一致；Scan5激发的第一和第四阶模态振型与数值仿真结果基本一致。由于所测得前四阶固有频率基本处于1～2 Hz以内，因此进一步精扫描时将扫描范围缩小至1～2.2 Hz。最终，偶数编号的精扫描获得系统频响结果及振型如图12和图13所示，相应频率值记录在表7中。

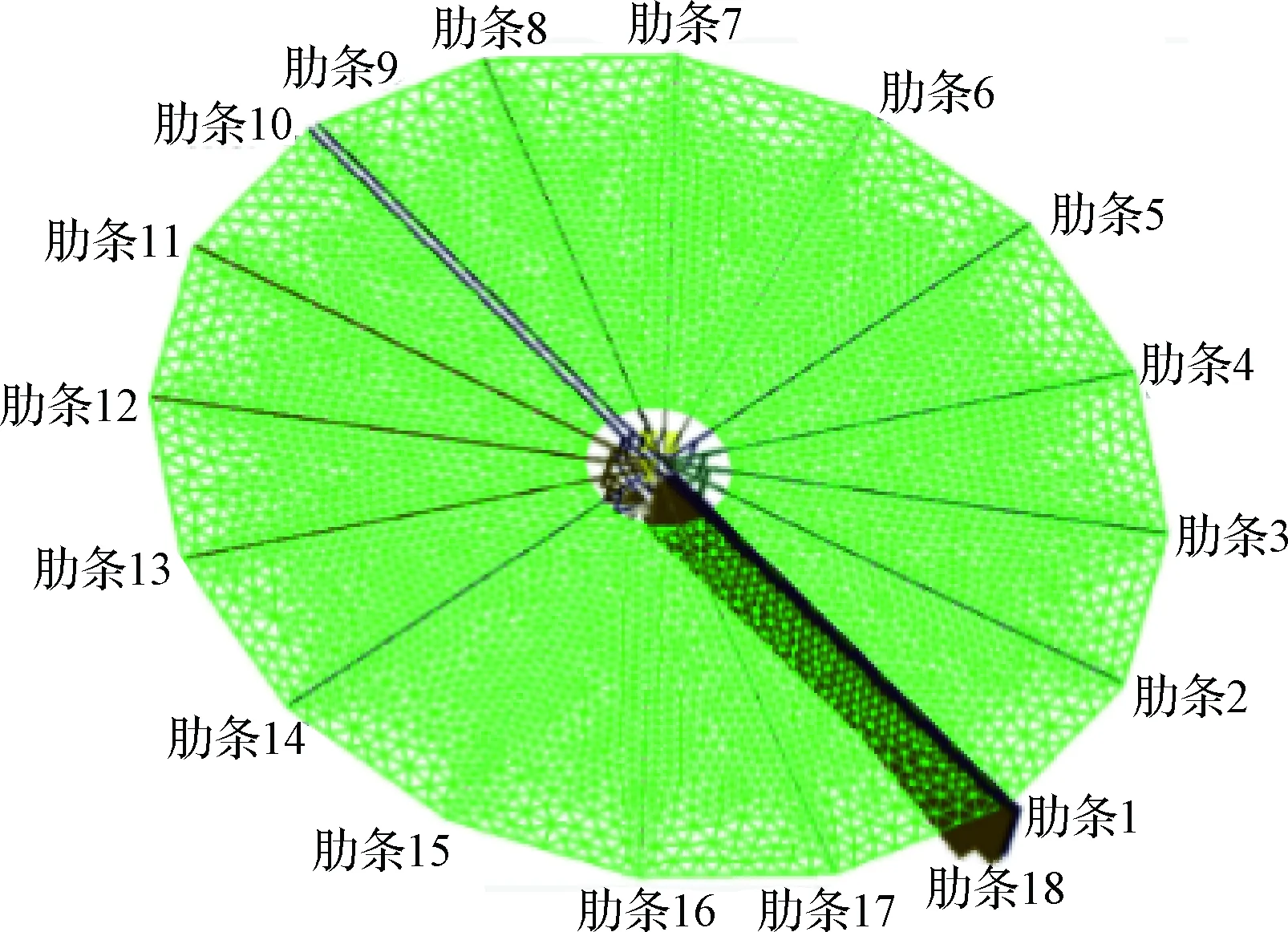
图11 圆形太阳翼肋条编号示意图

表6 圆形太阳翼模态测试工况Table 6 Modal test conditions of Circular Solar Arrays

表7 圆形太阳翼前四阶模态频率Table 7 The first fournatural frequency of Circular Solar Arrays

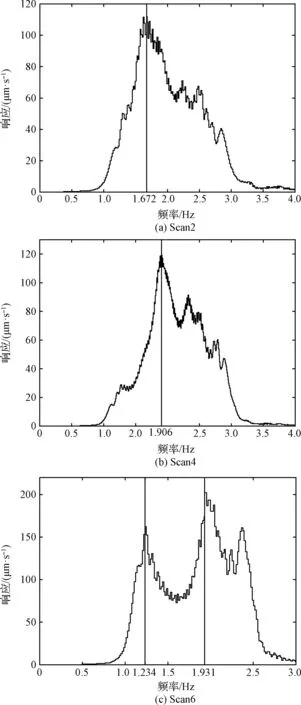
图12 精扫描获得太阳翼频响曲线

3 有限元模型修正

真实太阳翼样机存在机械间隙等使得柔性程度

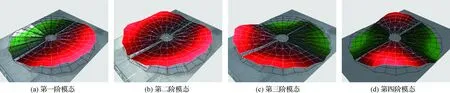
图13 圆形太阳翼前四阶模态

变高的影响因素。仿真时，应针对行进行模型修正以获得更为准确可靠的结果。有限元模型修正的主要方式通过改变系统刚度矩阵或质量矩阵从而影响模态分析的结果。而质量矩阵一般已知，但生产制造及不断收展等因素，系统的刚度矩阵难以测得。圆形太阳翼主要振动模式为离面振动，影响太阳翼模态的因素主要来自肋条和太阳毯。由前期数值分析可知，肋条模量对太阳翼模态频率的影响程度较大，因此可通过适当减小肋条模量以减小系统刚度矩阵，提高太阳翼有限元模型的柔性从而更为精确地仿真实际的地面模态试验状态。

在仿真前，需先调节太阳翼面预紧力使其与样机的试验状态相同，随后进行静力学分析得到刚度矩阵与质量矩阵并进一步开展模态分析。最后，将修正后有限元模型的结果与试验结果进行对比，得到可靠准确的修正模型，为以后类似的太阳翼模态的计算提供参考。

3.1 太阳翼静力学分析

为使数值分析结果与太阳翼试验状态一致，先用激光水平仪，选择翼面4、5、12、13进行下移量测量，所测得四组均值为24.025 mm。随后，对中心肋条绳索施加初始温度载荷20 ℃，并在随后0.1 s内线性下降至10 ℃并保持2.9 s。不断调节竖直向下的加速度使得太阳翼片中部下垂量靠近所测得数据结果。经分析发现，当肋条的弹性模量为32 Gpa、重力加速度为0.4 m/s2时，求得太阳翼Z方向位移结果与太阳翼实际的试验状态一致，可以进行后续的模态分析。

3.2 太阳翼模态分析

经SAMCEF软件计算，获得太阳翼的前四阶模态，修正前后的太阳翼有限元模型所得模态频率与试验数据误差如表8所示。可见，模型修正前，太阳翼前四阶模态频率与试验数据相差较大，其中，相差最大的为第一阶频率，达到了57.3%；经过刚度修正后的有限元模型所得频率与试验数据的误差减到4.16%之内。

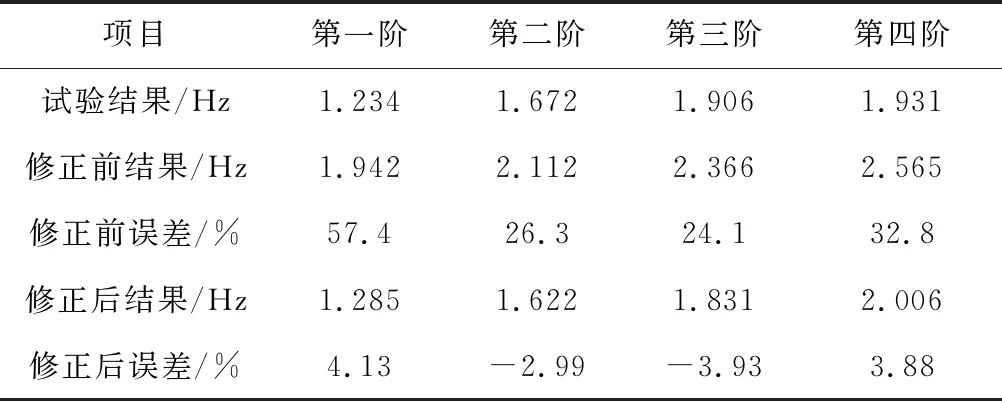
表8 圆形太阳翼模态频率误差Table 8 Thenatural frequency error of Circular Solar Arrays

4 结论

参考NASA对UltraFlex-175太阳翼的模态仿真及地面试验，以北京空间飞行器总体设计部研制的一种新型柔性太阳翼为参考模型，首先利用SAMCEF软件对影响太阳翼模态的敏感因素进行大量仿真分析发现：(1)太阳翼前两阶模态对预紧力变化不敏感，对第4至6阶模态频率影响较大，差值可达到10.36%；所以实际测量翼面下垂量应足够精确，且需在仿真前对模型施加相应预紧力载荷以保证仿真与试验状态高度一致；(2)支撑车约束方式主要影响太阳翼第一阶模态，差值约2.26%；有支撑车相比无支撑车，太阳翼的第一阶模态频率受到较大影响，差值达到32.89%；因此地面试验时，不能使用支撑车机构；(3)重力作用对试验的影响翼面预紧力一致；含悬吊弹簧的重力卸载系统可有效减轻重力作用对模态的影响；此外，研究发现，当弹簧刚度小于7 N/m时，其对太阳翼模态的影响小于0.59‰，可忽略不计。其次，结合仿真分析结果，采用激光扫描测振仪、双点激励方式以及硅胶管悬吊系统，先通过预试验优化了激振源等相关参数，再经过多次正弦扫频测试高效、精确地获得太阳翼前四阶模态振型与固有频率。相关试验方法首次应用于圆形太阳翼中，方案与NASA的太阳翼模态试验不同，且更为合理。最后，根据试验结果，所提供的一种简单有限元数值模型修正思路，可使修正后的数值仿真频率误差从57.3%下降至4.16%，符合测试相关标准的要求。