航天器太阳能电池阵驱动系统激扰因素辨识与扰动机理分析
2021-01-10朱仕尧雷勇军
朱仕尧,雷勇军,郭 欣
(国防科技大学空天科学学院,长沙 410073)
0 引 言
航天器太阳能电池阵驱动系统(Solar array drive system,SADS)一般由太阳能电池阵和太阳能电池阵驱动装置(Solar array drive assembly,SADA)两部分组成。随着航天任务对航天器性能要求的不断提升,SADS运转而产生的持续微幅扰动逐渐成为影响航天器高分辨率对地成像和远距离激光通信等核心性能的关键因素之一。
国内外学者对SADS驱动扰动问题开展了卓有成效的研究。欧空局于1989年在Olympas卫星上进行在轨测量[1],通过姿态角速度功率谱曲线发现SADS扰动同时包括低频和高频扰动成分。文献[2-4]建立了较为详细的直接驱动型驱动装置和太阳能电池阵动力学模型,其中考虑步进电机齿槽效应和负载柔性等因素。Sattar等[5]和Chen等[6]研究了带有刚性和柔性负载的驱动系统扰动特性问题,其中柔性负载采用集中参数模型模拟,并对步进电机进行线性化处理。Zhou等[7]提出了一种面向驱动控制的间接驱动系统动力学模型,并分析了齿隙和摩擦等齿轮传动系统非线性因素对电机速度稳定性的影响。Yang等[8]搭建了驱动装置与小惯量刚性负载系统动力学试验平台,并对电磁刚度和阻尼进行试验测试研究。Li等[9]将惯性负载与驱动装置之间增加柔性板结构,用于调节一阶扭转振动模态,并研究了扰动力矩频谱分布规律。程俊波等[10]建立了含永磁同步电机的SADS系统模型,采用模糊控制克服非线性摩擦影响,从而减少电池阵振动扰动。于登云等[11]采用固定界面模态综合法建立驱动系统模型,并总结了电流噪声和控制参数选取不当是引起扰动的主要原因。上述研究侧重关键部件的模型细化,并直接从扰动频谱特点判定激扰因素,但SADS扰动的分布频段较广、激扰因素较多,需要从系统模型出发分析扰动产生的本质原因、主要激扰因素以及其对扰动时频特性的影响。
本文在SADS扰动特性[12-13]和模态特性分析[14]基础上,综合考虑太阳能电池阵、驱动装置、驱动控制和减速装置等内部非线性因素及相互耦合作用,建立系统级驱动系统动力学模型,并通过地面试验验证其正确性;在此基础上,利用还原论思想,削减各种影响因素将驱动系统退化为无扰动的平稳运动状态,解释扰动产生的必要条件;进一步辨析激起驱动系统扰动的主要激扰因素,并定量分析各种因
素的影响规律,从而说明太阳能电池阵驱动系统的扰动机理问题。
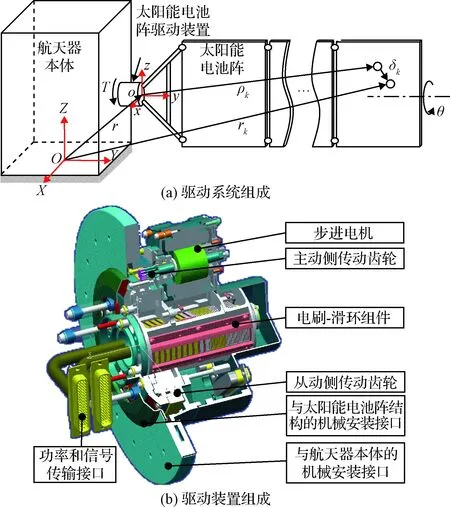
图1 太阳能电池阵驱动系统组成示意图
1 太阳能电池阵驱动系统动力学建模
典型太阳能电池阵驱动系统如图1所示,其中驱动装置主要包括驱动控制器、步进电机、电刷-滑环组件以及齿轮减速器等部件。建模假设如下:1)航天器本体结构为刚性体,并约束刚体位移和忽略推进剂消耗;2)忽略由驱动控制微处理器“数电-模电”转换引入的系统误差;3)忽略步进电机绕组磁滞、磁饱、互感效应等因素,且绕组自感参数不随转子位置变化;4)只考虑齿轮减速器在驱动方向的变形和位移;5)在小变形情况下,忽略太阳能电池阵基板和展开锁定装置的材料和连接非线性;6)电刷-滑环间摩擦远大于步进电机轴承摩擦。图2说明SADS工作流程可分为驱动控制、驱动执行机构以及太阳能电池阵等三部分。

图2 太阳能电池阵驱动系统典型工作流程
1.1 驱动控制模型
如图2所示,驱动控制包含参考电流生成器和绕组电流控制器两部分,分别实现转速开环控制和电流闭环控制功能。参考电流生成器根据脉冲驱动信号生成细分参考电流;绕组电流控制器将参考电流和绕组电流[15-16]的误差作为反馈,利用PI控制律调整电机绕组中驱动电压,保证绕组电流随参考电流变化:
(1)
(2)
(3)

1.2 驱动机构模型
如图2所示,在驱动电压作用下,驱动执行机构根据太阳能电池阵实际转角偏差调整驱动力矩。对于含有内啮合直齿轮减速传动机构的间接驱动型驱动装置,小齿轮对应步进电机驱动主动轴,其转速为步进电机的转速;大齿轮对应太阳能电池阵从动轴,其转速为太阳能电池阵的转速,如图3所示。
主动轴在电机力矩、啮合力矩以及电机转子惯性力矩作用下达到平衡:
(4)
式中:rb为小齿轮基圆半径;Jm为电机转子轴转动惯量;Te为定转子之间的电机力矩;Fg为齿轮传动力。对于两项混合式步进电机,可根据虚功原理得到电机力矩[14]:
(5)
式中:Kf为电磁力矩截断阶数;Nb为驱动拍数;Lmk和Lfk分别为定子绕组和虚拟转子绕组第k阶电感系数;前两项是由定子绕组和转子永磁体作用产生的电磁力矩,第三项是由定转子轮齿相互作用引入的齿槽力矩,其中含有驱动倍频成分。

图3 齿轮传动部件传动关系
此外,齿轮之间的动态啮合力与轮齿间相互配合密切相关,可以采用图3所示的啮合弹性力和阻尼力表征齿面间的动态传动力Fg(t):
(6)
式中:kg(t)为时变啮合刚度,其傅里叶级数展开为:
kg(2k)sin(kNtθm)]
(7)

(8)
其中,Δg为静态传动误差,其可以表示为[17]:
Δg(t)=rbθm-rfθa+e(t)=rbθm-
(9)
式中:θa为太阳能电池阵转角,rf为大齿轮基圆半径,e(t)为静态传动误差,ek为静态传动误差的谐波项幅值,Nt为小齿轮齿数。
从动轴在驱动力矩Ta、摩擦力矩Tf和齿轮传动力矩作用下达到平衡,其中从动齿轴摩擦力矩[18]主要由电刷-滑环组件提供:
Fgrf-Ta=Tf=σaωa+[Tc+(Ts-
Tc)exp(-ωa/ωs)]sgn(ωa)
(10)
式中:rf为从动轴转动惯量,σa为黏性摩擦系数,ωa为太阳能电池阵转速,Tc为库伦摩擦力矩,Ts为最大静摩擦力矩,ωs为stribeck临界转速。
1.3 太阳能电池阵模型
如图2所示,太阳能电池阵在驱动力矩作用下首先发生刚体转动,由此产生运动惯性力会激起结构柔性振动,并且振动引起的模态惯性力又会反向影响附件的刚体转动规律。根据虚功原理可以得到太阳能电池阵结构刚柔耦合振动微分方程[14]:
(11)
式中:Ha为模态角动量矩阵H的第二行向量,Ja为转动惯量矩阵J的第二个对角元,Ta为力矩向量T的第二个元素,η为太阳能电池阵模态坐标。
太阳能电池阵在三个平动和两个转动方向的广义约束力向量(即拉格朗日乘子向量λ)可以表示为:
(12)
式中:S和P为电池阵的静矩和模态动量矩阵。
1.4 系统模型组集
将式(10)中的驱动力矩Ta代入式(11),并与式(4)中的主动轴平衡方程联立得到SADS动力学方程:
(13)
1.5 试验验证
1.5.1扰振特性试验
如图4所示,试验对象由驱动装置(相关参数见文献[14])、太阳能电池阵模拟件及相关连接件组成。由于太阳能电池阵为多铰链连接结构,且持续转动,难以进行吊装,因此设计两块构型相同(尺寸为163 mm×400 mm×5 mm)的金属薄板模拟其在驱动方向的质量和刚度特征,使模拟件满足转动惯量(18 kg·m2)和频率(固支基频0.8 Hz)等效原则。在模拟件轴线方向配置吊装组件卸载重力,以减小结构重量对驱动装置轴承压力,使其更接近在轨状态。受限于结构件尺寸较大,试验室尚不具备模拟高真空和温度梯度等空间环境的能力。测试系统由Kistler测力平台、Polytec激光测振仪、信号放大器、数据采集器、计算机和驱动装置控制器以及试验数据分析软件等组成,如图4所示。测力平台与驱动装置固定连接,用于测量驱动方向扰动力矩分量。将激光测振仪测点设置在太阳能电池阵刚性转接工装上,在低转速和忽略工装弹性变形前提上,可通过测点线速度比例换算得到电池阵实际转速。测量数据分别经过信号放大器和测振仪后置端进行处理,并利用数据采集器传递给计算机;外置驱动器用于产生驱动装置所需驱动信号,控制太阳能电池阵转动和停止。

图4 驱动系统扰动特性测试系统
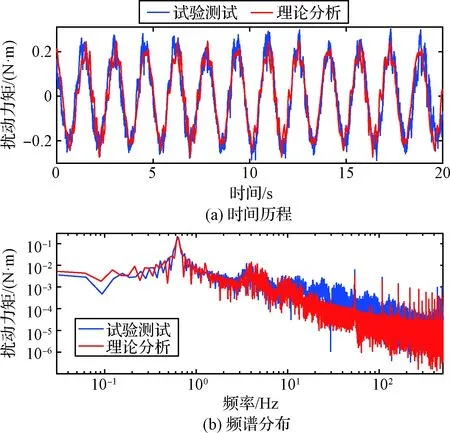
图5 稳态扰动力矩分析结果与试验测试数据
1.5.2试验结果分析
选取驱动系统转速稳定后的扰动力矩响应,经过消除趋势项等数据预处理后得到离散时域数据,并利用傅立叶变换获取对应的频域数据。通过调整步进电机的电磁力矩系数修正驱动系统一阶固有频率,使其更接近试验测试数据;并利用频谱分布特点,在系统模型中设定第1,3,16,17和18阶电磁力矩成分,并对力矩幅值优选得到取值分别为0.054 N·m,0.054 N·m,0.027 N·m,0.027 N·m和0.027 N·m。扰动力矩分析结果与试验数据如图5所示,其中稳态扰动力矩时间历程和频谱分布曲线与试验结果非常接近,相对误差小于10%,如表1所示。综上,所建立的系统动力学模型可以较为准确地预估驱动系统的稳态扰动规律。

表1 理论分析和试验测试结果对比Table 1 Comparison of disturbance characteristics between analysis results and experiment data
2 驱动系统激扰因素辨析
在驱动方向上,驱动系统对航天器本体的扰动力矩等于太阳能电池阵驱动力矩的反作用力;在非驱动方向上,广义扰动力等于航天器本体对驱动系统的约束力。根据力矩平衡方程式(11)和广义约束力表达式(12),得到驱动系统对航天器本体的广义干扰TD:
(14)
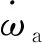
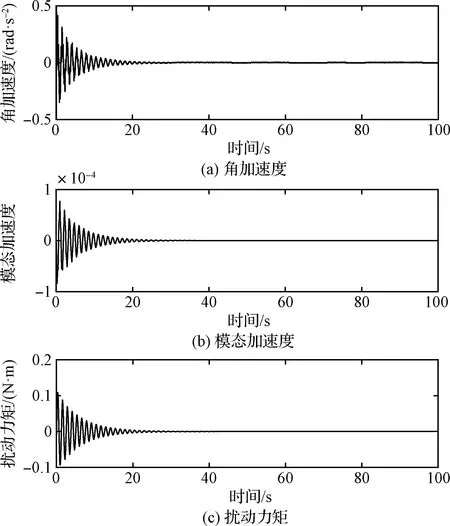
图6 平稳运动假设条件下的驱动系统响应时间历程曲线

3 激扰因素的扰动特性分析
本部分通过构建单一激扰因素作用环境,逐一分析各激扰因素的扰动特性。在对线性因素分析时会引入系统固有频率予以辅助,以某型卫星太阳帆板结构为例,其质量39.4 kg,绕驱动轴线转动惯量为21.5 kg·m2,固支状态下一阶扭转频率为1.813 Hz;与直接驱动型SADA(驱动力矩为2.1 N·m,电机齿数为300)组成驱动系统后,由于电机转动方向的电磁刚度影响,系统整体的一阶扭转频率降为0.796 Hz。
3.1 电流细分激扰特性分析
整步驱动的步进幅度较大,每次步进所激起太阳能电池阵转角和振动幅度也相对较大,会在一定程度上影响系统运动规律。现代驱动装置往往应用电流细分技术对步进角度进行细分,但是细分步进仍然会引起系统角加速度的脉冲变化,影响驱动系统的扰动规律。如图7所示,电流细分引起的扰动力矩变化具有周期性变化规律,每个细分微步均会引起扰动力矩突变,并伴随出现最大扰动力矩。扰动幅度随着细分数的增大而逐渐减小,扰动成分主要分布在细分频率附近,且扰动频率基频(即细分频率)随细分数增大而正比例放大。

图7 细分驱动扰动特性分析
3.2 非线性电磁场激扰特性分析
3.2.1齿槽力矩激扰特性分析
步进电机的定子和转子均为多齿结构,在转动过程中两者之间的轮齿相对位置周期性变化,导致齿隙磁通量发生周期波动,引入具有高阶谐波成分的齿槽力矩。如图8(a)所示,齿槽力矩所激起的扰动力矩均为周期变化,但不同幅度的齿槽力矩所激起扰动的变化规律有所不同;随着齿槽力矩幅值增大,扰动力矩波动幅度逐渐放大,并且多频叠加振动效果更加明显;如图8(b)所示,扰动成分主要分布在前几阶激扰频率处;如图8(c)所示,在所有齿槽激扰阶次工况对比中,扰动力矩幅度均随激扰幅值增大而增大,但明显呈现非线性对应关系;当激扰频率或倍频与系统扭转模态固有频率接近时,扰动幅度明显增大。

图8 齿槽力矩扰动特性分析
3.2.2高阶电磁力矩激扰特性分析
在Δθm取值较小,且较为稳定时,电磁力矩一阶分量可以近似认为是角度误差的比例控制环节,保证驱动负载按照指定的驱动规律运动:
Te1=Lm1ImNmifsin(NmΔθm)≈Lm1ImNmifNmΔθm
(15)
然而,步进电机在生成一阶电磁力矩的同时也会产生高阶电磁激扰力矩分量。高阶电磁力矩表现为随角位移变化的正弦函数关系:
Tek=kLmkImNmifsin(kNmθm-Nmθm+NmΔθm)
(16)
如图9(a)所示,电磁激扰作用下所产生的稳态扰动力矩均呈现周期性变化特点;当激扰阶次较低时,所激起的结构模态振动响应较小,单频振动特点明显;当激扰阶次增大至五阶之后,扰动力矩表现为多种频率波动的叠加;如图9(b)所示,扰动成分集中在电磁激扰频率及其倍频附近,并且频谱峰的取值和数量均随着激扰阶次的提高而逐渐增大或增多;当激扰频率的高倍频与系统一阶扭转频率较为接近时,其频率分布幅值会明显增大,例如:六阶激扰时的激扰频率与系统一阶扭转频率接近,其对应的频谱峰值可能会超过激扰频率。在所研究范围内,扰动幅度均随着激扰阶次和幅度的提高而逐渐升高,如图9(c)所示。

图9 高阶电磁力矩扰动特性分析
3.3 齿轮传动激扰特性分析
3.3.1齿轮啮合刚度和阻尼的激扰特性分析
与直接驱动不同,间接驱动型驱动装置内部包含齿轮减速环节。在齿轮啮合过程中,轮齿啮合刚度和啮合误差会随着轮齿间相对位置改变而周期性变化,所以啮合刚度和啮合误差会引起系统刚度或运动位移的波动,导致驱动系统发生参数自激振动,引起不平稳运动并产生系统扰动。
考虑一阶啮合刚度和啮合误差变化情况下的稳态扰动力矩如图10(a)和图10(b)所示,其中k0和e0分别为2×106N/m和0.01°,且k1/k0=e1/e0=0.1。啮合刚度引起的稳态扰动力矩具有周期变化特点,每个周期内的扰动力矩具有啮合频率及其倍频两种波动频率;类似地,啮合误差所引起的稳态扰动力矩同样具有周期变化特点,但每个周期内部的扰动力矩仅包含齿轮啮合频率一个主要波动频率。如图10(c)所示,在所研究的参数范围内,扰动力矩幅值均随啮合刚度和啮合误差的时变分量与恒定分量的比值(即k1/k0和e1/e0)的提高而逐渐显著增大。

图10 时变啮合参数扰动特性分析
3.3.2齿轮啮合间隙的激扰特性分析
齿轮主动轮齿和被动轮齿之间的配合间隙是引起齿轮传动非线性的重要因素之一。图11(a)给出了只包含齿侧间隙因素情况下的系统响应时间历程曲线,其中齿侧间隙为0.001 m。不难发现在起动阶段,主动轮齿和被动轮齿之间的相对位移迅速达到间隙上限(即发生齿侧碰撞),并在0.8 s附近分离后又发生二次碰撞,导致扰动力矩迅速增大;在系统阻尼作用下,扰动力矩逐渐衰减,轮齿间相对位移始终保持在间隙上限,稳态扰动力矩逐渐趋近于零,说明齿侧间隙因素只会改变起动阶段的扰动特性,不是引起系统稳态扰动的直接因素。
然而,齿槽间隙仍然是影响系统扰动特性的重要因素。如图11(b)和图11(c)所示,当齿侧间隙为0.002 mm时,一阶齿槽激扰幅度变化会导致系统响应规律明显改变:1)激扰幅度为0.2 N·m时,主动和被动轮齿之间的相位位移始终为间隙上限,没有出现啮合面分离现象,扰动力矩连续稳定变化,并呈现单频率周期波动变化特点。2)激扰幅度增大至0.4 N·m后,主动和被动轮齿之间的相位位移大部分时间内处于间隙上限,但在特定时间节点位置出现周期性的瞬时减小并迅速恢复,即出现齿侧分离和碰撞;此时扰动力矩仍呈现周期性波动特点,但在齿侧再次碰撞时会明显提高。3)激扰幅度进一步增大至0.6 N·m,主动和被动轮齿之间的相位位移在间隙上限和下限间周期变化,即主动轮齿与前一被动轮齿分离,并与后一被动轮齿发生碰撞;当主动轮齿与被动轮齿再次配合时,扰动力矩会瞬时增大,然后迅速减小,扰动幅度明显大于前两种情况。
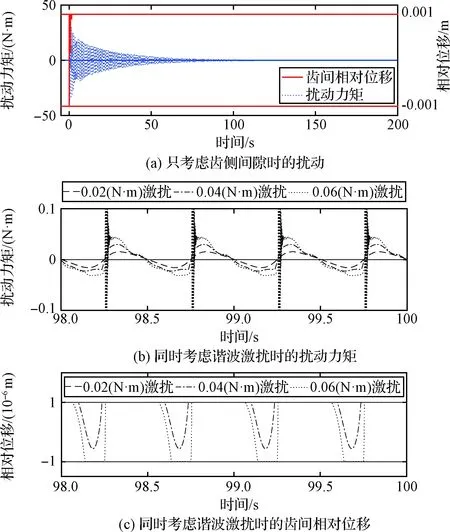
图11 考虑齿侧间隙情况下的驱动系统响应时间历程曲线
4 结 论
针对太阳能电池阵驱动系统扰振机理问题,本研究分析了诱发扰动的前提条件、系统主要激扰因素以及各类激扰的时频域特点,对航天器驱动系统振动抑制具有重要的参考价值。主要结论如下:
1)所建驱动系统动力学模型考虑了内部耦合关系、非线性因素以及参数时变特性,并通过地面试验验证了模型正确性。
2)转动角加速度和振动加速度不同时为零是引起驱动系统扰动的前提条件;电流细分、齿槽效应、高阶电磁力矩分量、齿轮啮合状态时变等因素为驱动系统的主要内部激扰因素。
3)激扰因素激起的扰动力矩一般均具有周期性;扰动成分集中在激扰频率及其高倍频附近;扰动幅度随电流细分数增大而减小,随齿槽激扰幅度、电磁激扰幅度和啮合参数变化幅度增大而明显提高。
