非等距网格上一维对流扩散方程的保正格式

兰 斌, 王 涛

(1- 北方民族大学数学与信息科学学院，银川 750021;2- 宁夏智能信息与大数据处理重点实验室，银川 750021)

1 引言

对流扩散方程是一类基本的运动方程，其广泛应用于很多领域，如环境科学、能源开发、流体力学和电子科学等.在考虑辐射流体运动过程中，随着温度上升，光辐射逐渐在能量传输中占据主导地位，引起物质状态发生变化，变化的物态又反过来影响能量的传输.这是一类多介质大变形非线性耦合特征鲜明的复杂问题，研究内涵十分丰富，目前严格的理论研究难度大、进展较少，且实验研究受实验条件和成本的制约，因此，数值模拟是主要的研究手段.另外，在实际应用中，对具有极高密度比的物质界面分辨精度的要求非常苛刻，通常需要在拉氏(Lagrange)网格上进行计算；然而，在这个过程中，网格可能会随着流体的运动而发生扭曲和变形，甚至有凹网格和翻转网格的出现，这种大变形网格给具有间断问题的非线性能量方程组的数值求解带来极大困难.而现存的很多格式在求解该类问题时存在很多问题，诸如计算过程不收敛或收敛很慢，计算精度大幅度下降，出现非物理解或数值振荡等等，最后导致数值结果失真而失去意义.另外，为适应一些实际问题的求解，诸如能量传输问题，要求温度非负；质量传输问题，要求浓度非负等等.因此，对于离散格式来说，保正性是一个关键点.在输运与热传导中，一个不满足保正性要求的格式很可能会违反热力学第二定律的熵条件，引发热流从低温区流向高温区.Sharma 和Hammett[1]指出，在温度变化较大的区域内，容易导致温度出负；但对于格式的健壮性来说，温度的正性是必须的.

采用经典的有限差分法或标准的有限元法往往得不到我们想要的结果.比如，传统的迎风格式会因计算精度过低而易出现假扩散现象；而中心差分格式在一定条件下易引起非物理性的数值振荡等等.为适应不规则区域问题的求解，采用有限体积法，即以方程的守恒形式出发，对计算域作一系列网格单元(控制体)剖分，然后在每个单元上进行积分，通过散度定理将其转化为单元边上的积分形式，再对边上的通量作相应的离散.此方法能够适应于各种守恒型问题的数值模拟，它能始终保持数值通量的局部守恒性，这一特性能够清晰地显示出它的优越性.

近年来，科研工作者对扭曲网格上对流扩散方程满足保正性要求的离散格式做了大量的工作.Le Potier[2]在非结构三角形网格上提出了一个适用于强各向异性扩散系数的单元中心型非线性格式，但该格式只有当时间步长充分小的时候，系数矩阵才能在网格没有限制性条件下满足单调性.Lipnikov 等人[3]发展了Le Potier 的非线性格式，但却依赖于扩散系数以及网格单元本身.后来，Yuan 和Sheng[4]提出任意星形网格上求解扩散方程的保正格式，且不需要对所选取的多边形网格附加任何的正则性等限制性条件，同时，可很好地处理间断、各向异性等问题，并显式的给出了单元边上法向通量的离散表达式，因此，从总体上大大地改进和推广了上述的格式.Lipnikov 等人[5]基于文献[4]中关于向量的分解办法，给出一种不需要任何顶点辅助未知量的非线性两点通量逼近方法.文献[6]指出，已存在的部分单元中心型保正格式要求假设辅助未知量非负，但这并不一定总是成立，尤其是涉及到大变形网格情形.后来，文献[7]构造了一新的完全保正格式，即在无需假设辅助未知量非负的前提下可满足保正性要求.关于对流项的离散，也出现了大量的工作[8-16]，他们在离散过程中，为避免数值振荡，大都需要引入限制子技术，而部分问题的求解伴有降阶情形.因此，文献[17]提出了一种新的不含限制子技术的对流扩散方程的保正格式.

现考虑如下一维稳态对流扩散方程

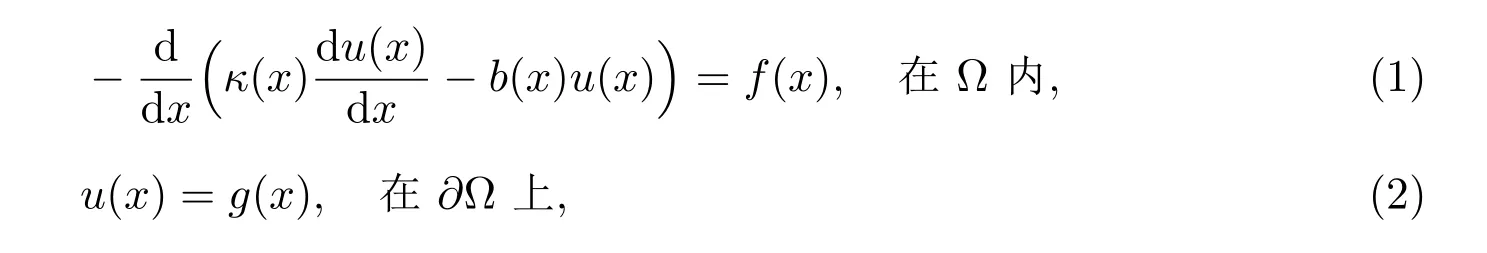
其中Ω 代表有界区域[l1,l2]，∂Ω 是其边界，κ(x), b(x)分别是扩散项和对流项的系数，f(x)为源项.

本文拟构造任意非等距网格上的保正格式，旨在揭示文献[15-17]中关于2D 对流扩散方程保正格式构造的机理.其中，扩散通量的离散在非等距网格上是线性的，而在等距网格上，当扩散系数为标量时可退化为标准的二阶中心差分格式；而对流通量的离散，为避免数值振荡，对区间端点值的逼近，可在上游单元中心处作Taylor 级数展开，然后利用相关辅助未知量完成梯度值的重构，将计算精度提高到二阶，并对出负单元作正性校正，以满足格式的保正性要求.

2 通量离散

将区间[l1,l2]任意剖分为互不重叠的子区间Ii:= [xi−1/2,xi+1/2], i = 1,2,··· ,N，即

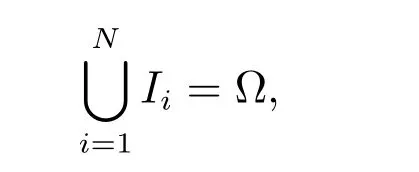
Ii∩Ij当i ̸=j 时最多只有一个交点，如图1 所示，其中x1/2=l1, xN+1/2=l2.

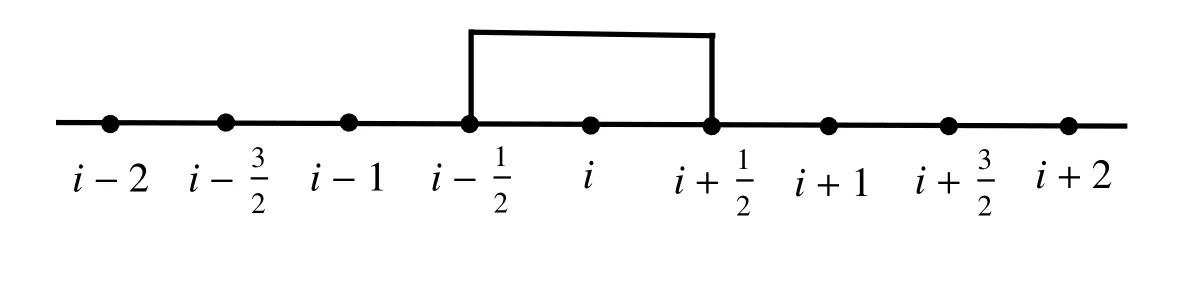
图1 网格模板图

定义hi= xi+1/2−xi−1/2, i = 1,2,··· ,N，而h = max{hi, i = 1,2,··· ,N}，对方程(1)在区间Ii上进行积分，即

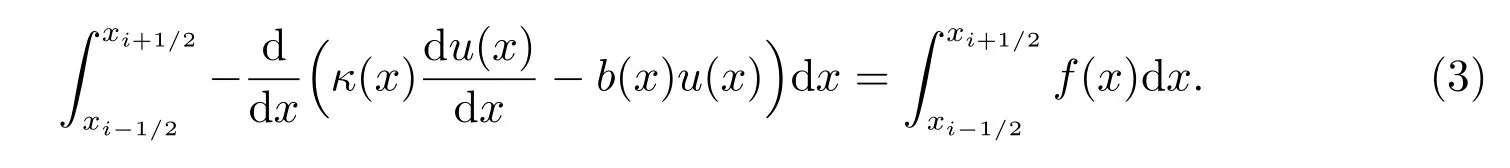
利用格林公式，得到

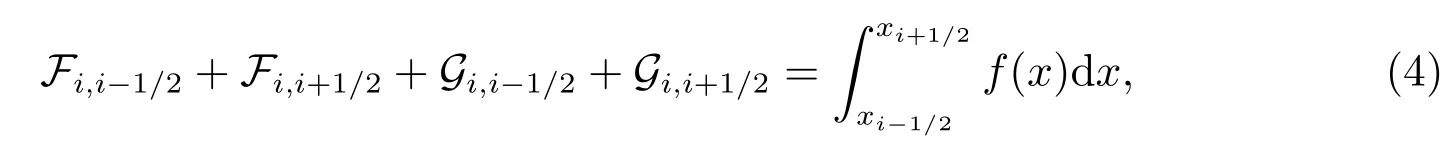
其中

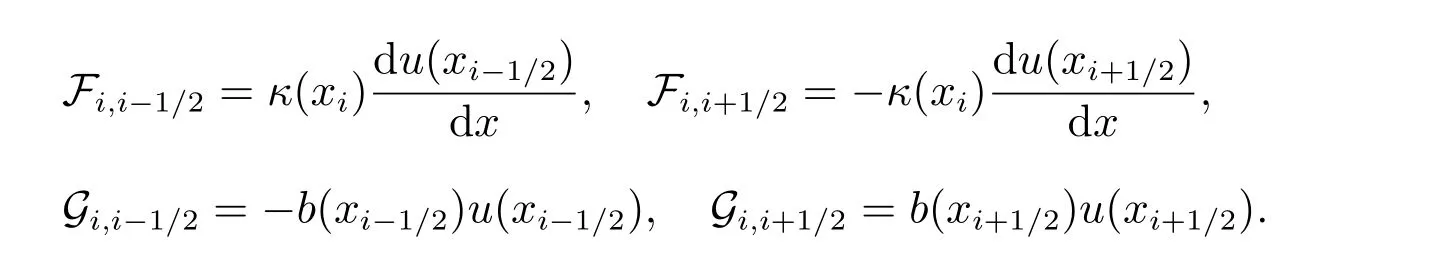
2.1 扩散通量

考虑扩散通量的离散.可定义方程(4)中的前两项为

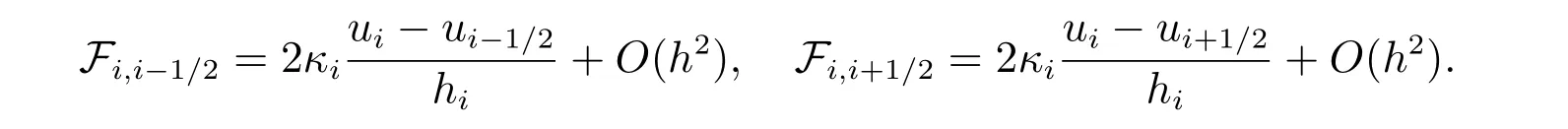
略去上两式的高阶项后，扩散通量的离散形式可定义为如下具有二阶精度的表达式，即

在两端点处给出通量的守恒型条件，即

为保证区间端点处通量的守恒性，即有

于是，可分别解得区间端点值，即

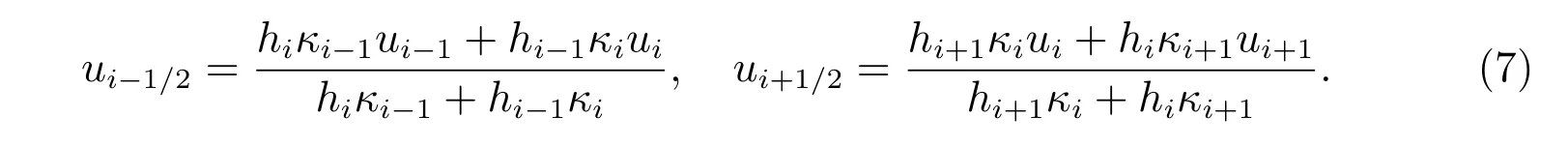
然后，将式(7)代入式(5)中，经整理，可得

最终，扩散通量的二阶离散格式可整理为

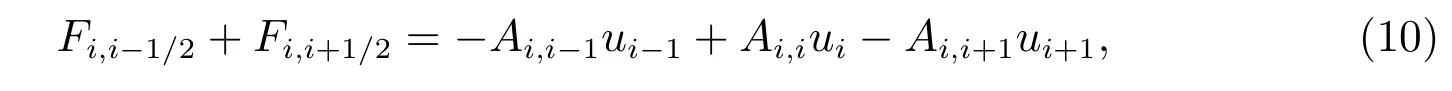
其中

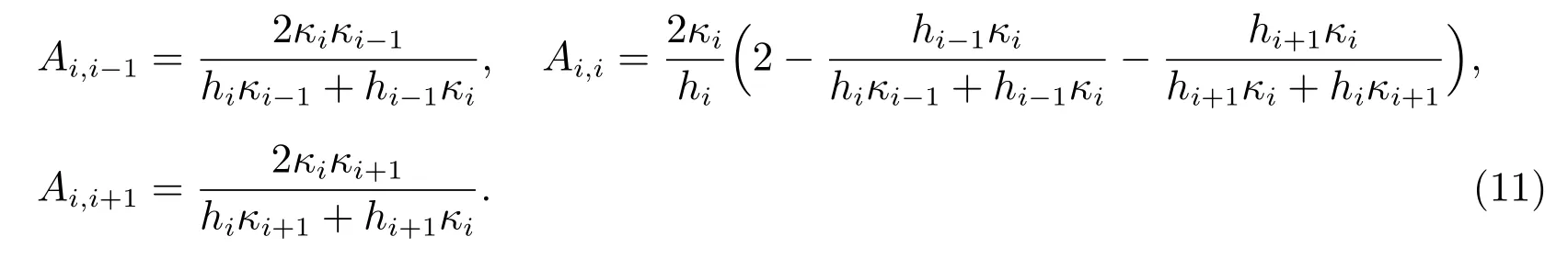
易证，线性方程(10)中的系数Ai,i−1, Ai,i, Ai,i+1均为正，且格式满足离散极值原理.

接下来，考虑边界单元的情形.当i=1 时，由上述推导，可得

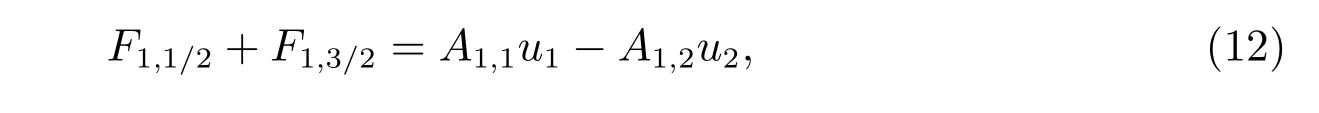
其中

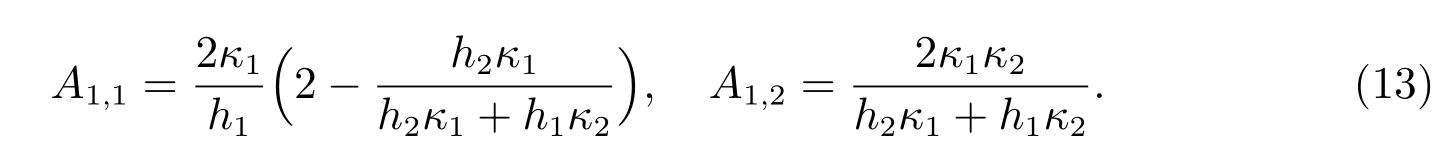
同理，当i=N 时，有

其中

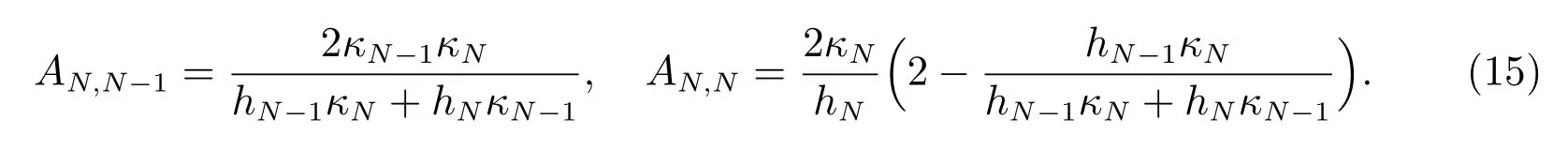
特别指出，如果是等距网格剖分，且扩散系数是一个常数κ0，那么式(10)可写成

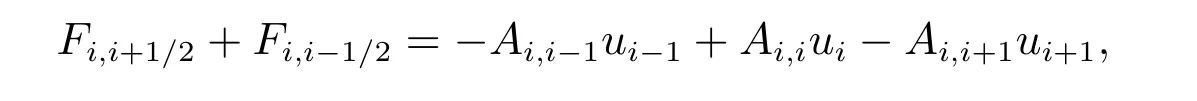
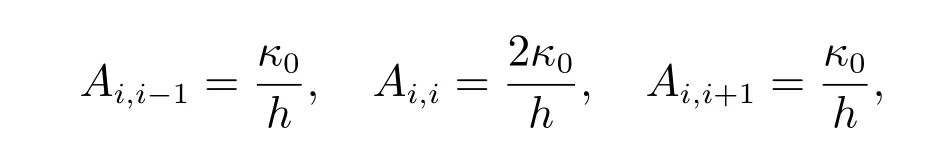
其中即格式退化为标准的二阶中心差分格式.

2.2 对流通量

由方程(4)出发，有

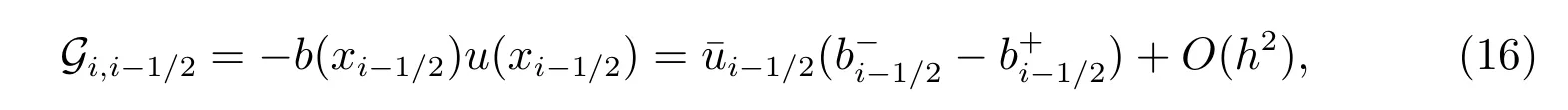
其中

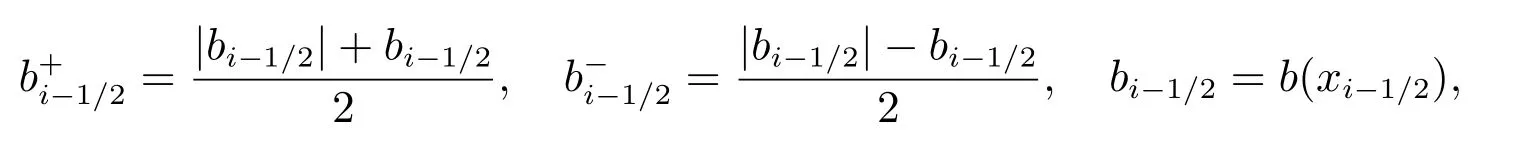
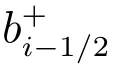
同样地

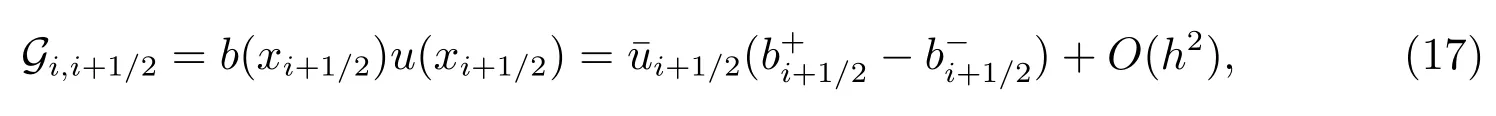
其中

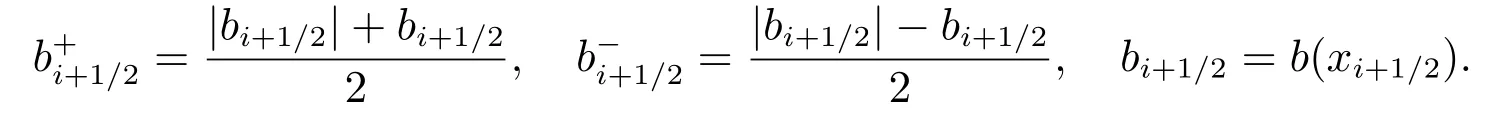
于是，为匹配精度，对端点值的逼近可利用Taylor 级数展开法，在上游单元中心处进行展开至保留梯度项，即

类似地，可得

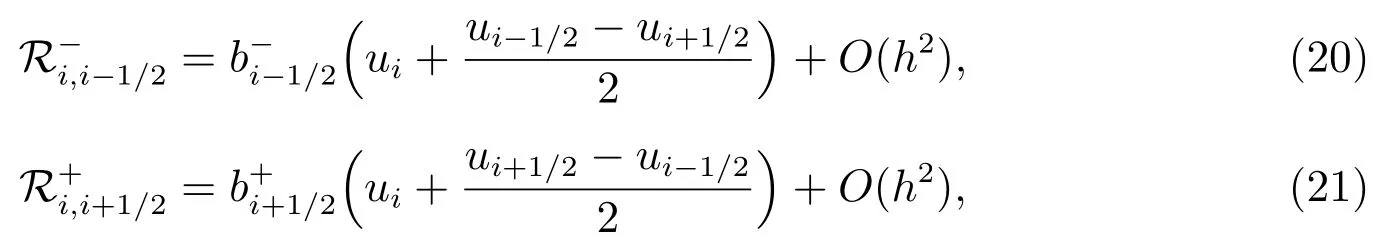
略去式(19)-(22)中的高阶项后，连续对流通量(16),(17)求和后的离散格式可表示为

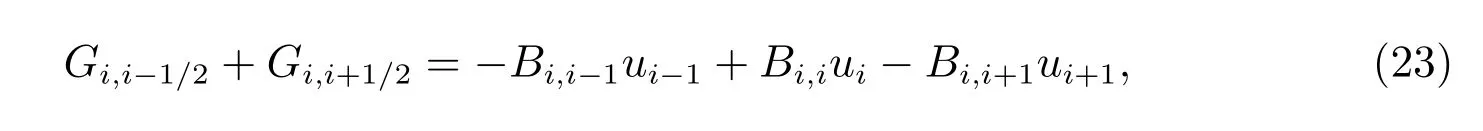
其中

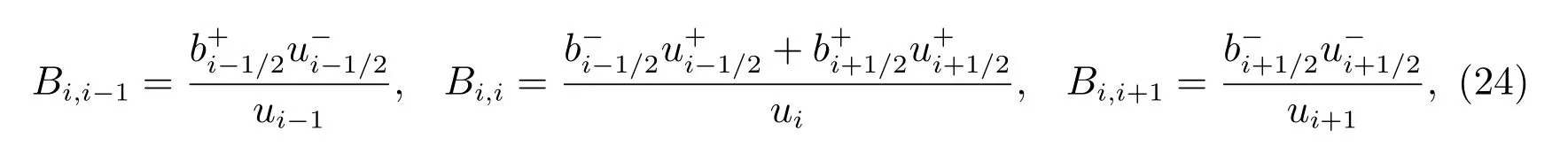
并且

其中ui−1/2, ui+1/2等节点值的计算可由式(7)给出.

再考虑边界单元.当i=1 时，由上述推导，可得

其中

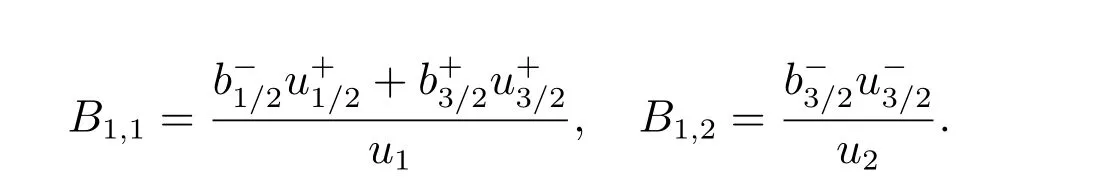
同理，当i=N 时，有

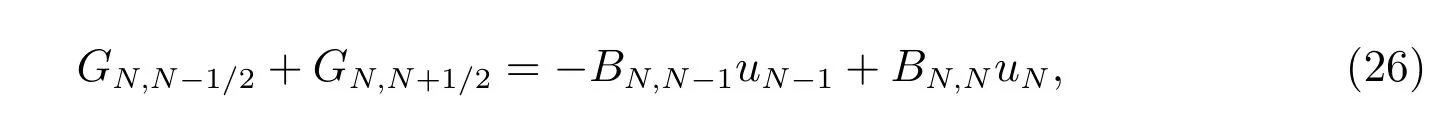
其中

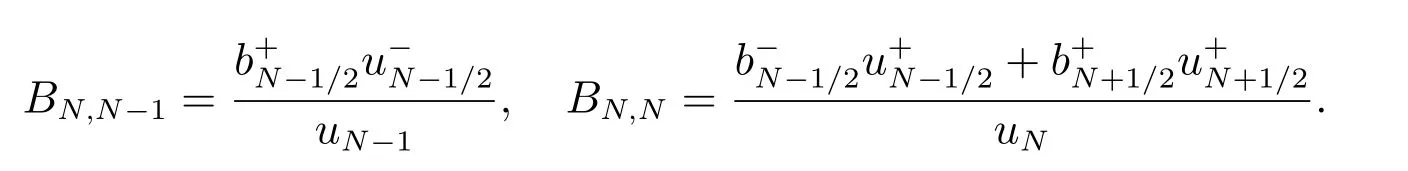
注1 为达到保正性要求，方程(23)中的相关系数必须满足保正性要求，即

2.3 保正格式

2.3.1 有限体积格式

结合扩散通量的离散(10),(12)和(14)以及对流通量的离散(23),(25)和(26)，方程(1)和(2)的有限体积格式可以写成如下形式

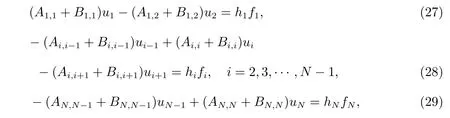
其中fi=f(xi), i=1,2,··· ,N.

2.3.2 非线性方程组

令U 为待求未知量所组成的向量，很显然，三对角方程组(27)-(29)所形成的系数矩阵是非线性的，记为A(U)，那么，该方程组可表示为

而非对称系数矩阵A(U)满足如下性质：

1) A(U)的所有主对角元素为正；

2) A(U)的所有非主对角元素为非正；

3) A(U)中所有列和均非负，并且至少存在一个列和的值为正.

因此，A(U)是按列弱对角占优的.我们采用Picard 非线性迭代方法求解非线性系统(30)：任意选取较小的值Enon> 0 以及任意初始向量U0> 0，使用非线性迭代指标s=1,2,···，重复执行以下过程：

1) 求解A(Us−1)Us=F；

2) 如果

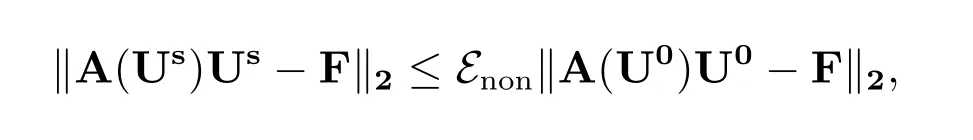
则计算终止.

对于线性方程组A(Us−1)Us= F，可采用Gauss-Seidel 迭代法进行求解，直到残差小于给定的值Elin，则计算终止.

2.3.3 算法

在这里，将给出具体的算法描述.

1) 任取初始U0>0, Enon和Elin.

2) 当s=0 时，

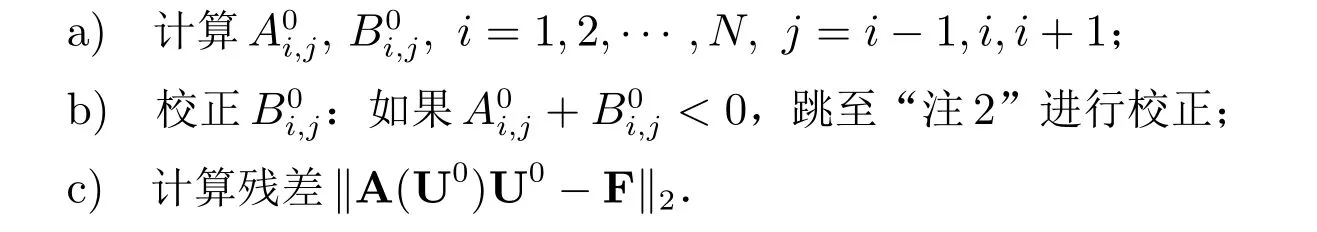
3) 当s=1,2,··· 时，

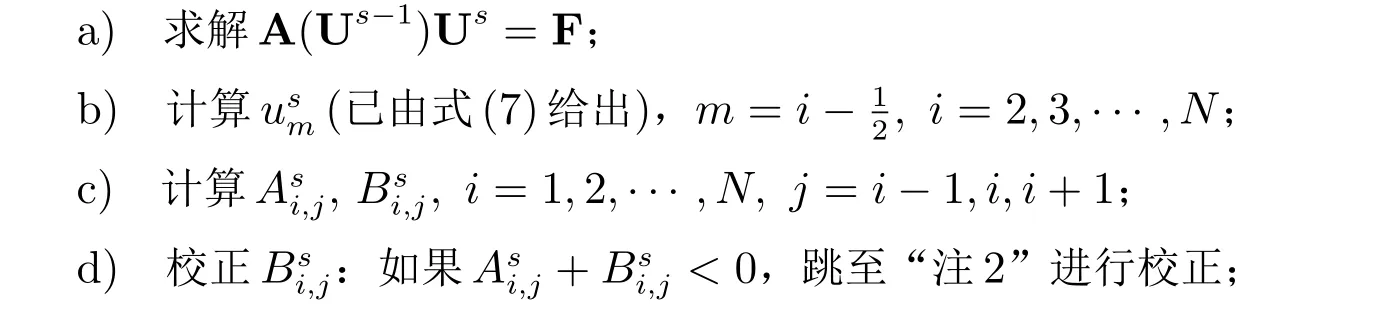
e) 计算残差‖A(Us)Us−F‖2；

f) 当‖A(Us)Us−F‖2≤Enon‖A(U0)U0−F‖2时，则跳至4)，否则返回至3).

4) 终止.

2.3.4 保正性

在证明保正性前，首先引入如下引理[4,18].

引理1 对于满足aii> 0(1 ≤i ≤n)和aij≤0(1 ≤i, j ≤n, i ̸= j)的不可约矩阵A=(aij)n×n，如果A 是按列弱对角占优的，即

且至少有一个不等式是严格大于0 的，则矩阵A 是一个M 矩阵[19,20].

于是，有如下定理成立.

定理1 令F ≥0, U0≥0，假设Picard 迭代中的线性方程组可以精确求解，则所有迭代向量Uk均为非负向量，即Uk≥0.

证明 在第2.3.2 小节中，我们给出了系数矩阵A(U)的一些性质.因此，它的转置满足引理1 中的条件，即AT(U)是一个M 矩阵，也即(AT(U))−1的所有元素均非负.因此，由(AT(U))−1= (A−1(U))T可知，A−1(U)也是非负的.如此，对任意的U ≥0, A(U)是一单调矩阵.

由于任意初始非负向量U0≥0，现假设正整数k0> 0，成立Uk0−1≥0.于是，系数矩阵A(Uk0−1)是单调矩阵，也即A−1(Uk0−1) ≥0 恒成立.当F ≥0 时，我们得到方程A(Uk0−1)Uk0= F 的解向量Uk0是完全非负的，即有Uk0≥0.因此，更具一般性地成立如下结论

Uk≥0, ∀k ≥0.

3 数值实验

本节将用两组不同算例的数值结果来验证本文格式的有效性.首先，引入L2范数

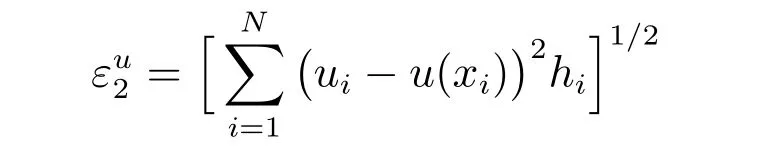
来定义计算解的截断误差，并取εnon= 1.0E −6 及εlin= 1.0E −10.而收敛阶可由如下公式给出，即

其中N1和N2分别代表不同的网格单元数，而Error(N1)和Error(N2)分别代表其对应的L2误差.对计算域作任意网格剖分，对任意内节点坐标x，可取

x:=x+σξxh,

其中ξx为介于−0.5 到0.5 之间的随机数，σ ∈[0,1]为扰动参数，h 为等距网格情形时的步长.

取Ω=[0,1]及b=1.0，问题的精确解以及扩散系数为

其中c=1,100; k0=1.0,10−6.

为了验证格式的精确性，我们将分别在等距网格和非等距网格上进行问题的求解.表1 至表4 分别给出了当扩散系数连续和间断时，在不同网格上数值解的L2误差及其对应精度的比较.

从四个表中数据可以看出，无论是在等距网格上还是非等距网格上，当扩散系数连续(c = 1)和间断(c = 100)时，均随着扩散系数的降低，即问题的求解由扩散占优逐渐向对流占优情形转变的过程中，数值解的精度均可达到二阶.表明本文格式适用于任意网格上扩散占优和对流占优问题的求解.现取网格数为48 时，在四种情形下，数值解的最小值均为4.085E −2，即格式满足保正性要求.图2 给出了非等距网格上，当网格点数取24，k0=10−6时，扩散系数连续(图左)和扩散系数间断(图右)时的计算结果示意图，可以看出，计算解与精确解吻合得很好.

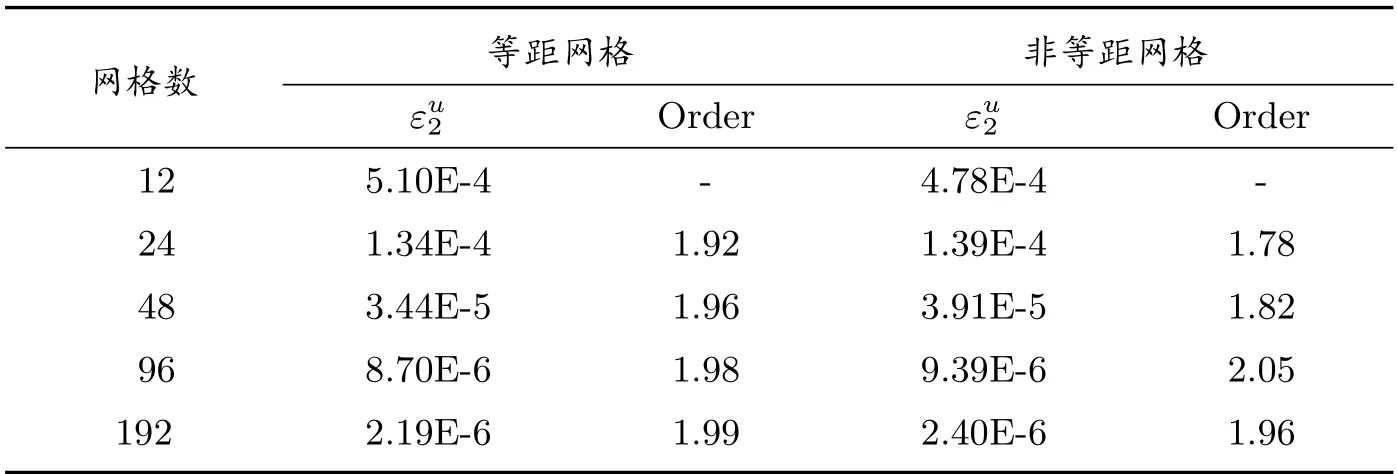
表1 扩散系数连续时的计算结果(c=1, k0 =1.0)

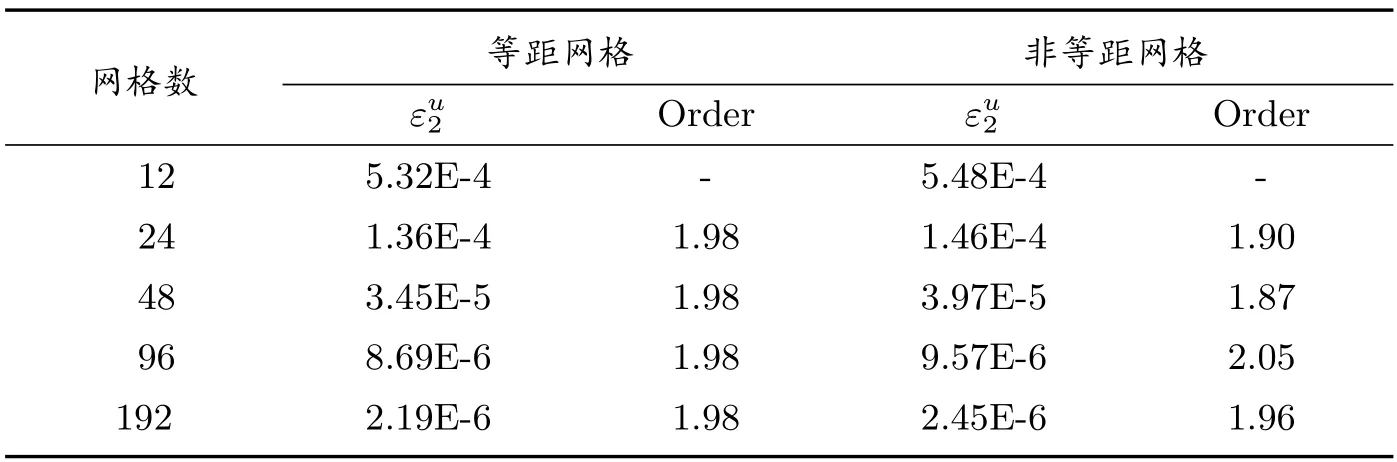
表2 扩散系数连续时的计算结果(c=1, k0 =10−6)

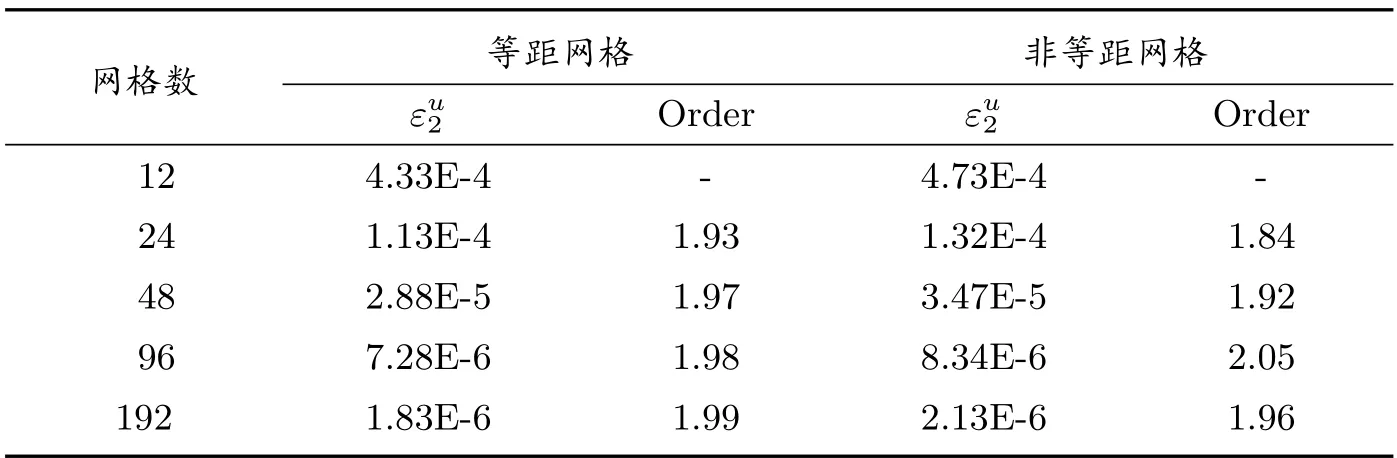
表3 扩散系数间断时的计算结果(c=100, k0 =1.0)

表4 扩散系数间断时的计算结果(c=100, k0 =10−6)

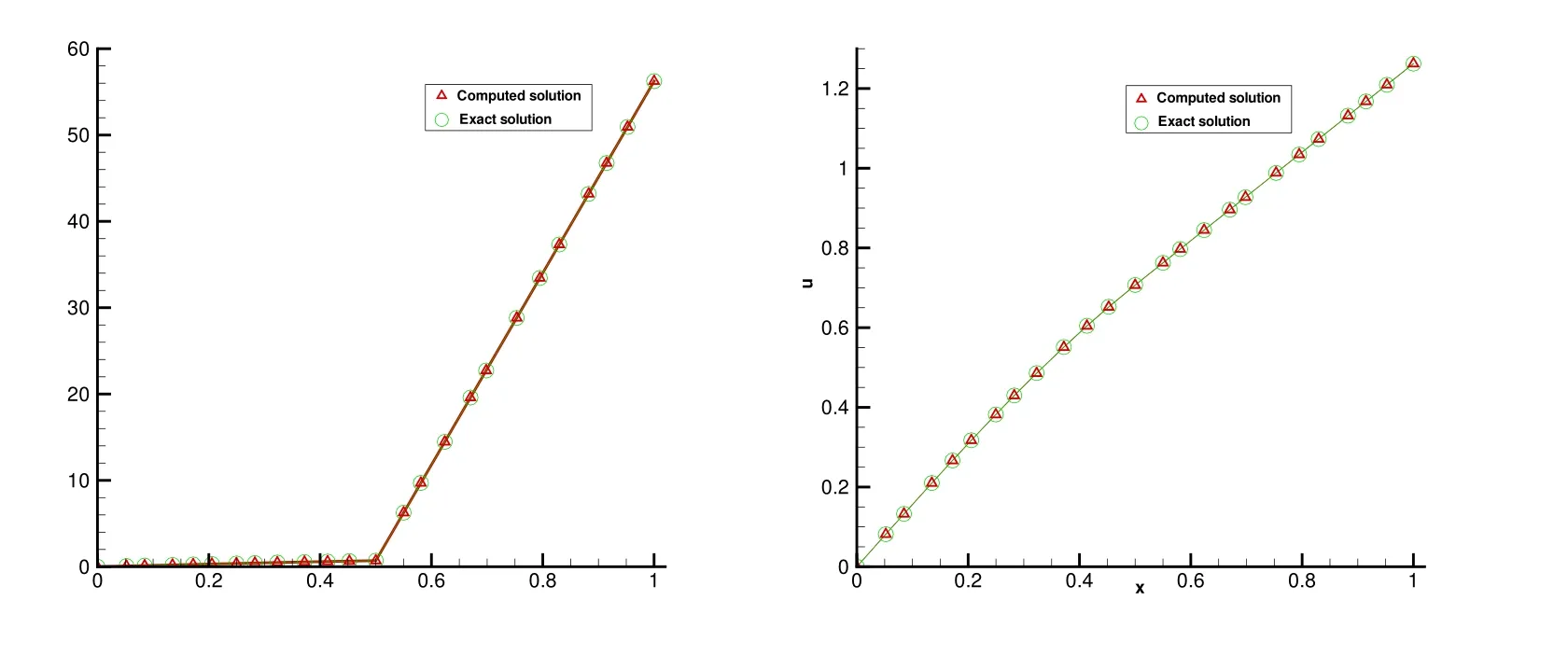
图2 非等距网格上计算结果示意图

4 结论

本文构造了任意非等距网格上一维稳态对流扩散方程的保正格式. 其中，关于扩散项的离散，在等距网格上，当扩散系数为标量时，任意内区间两端点处的扩散通量可退化为标准的二阶中心差分. 而对流项的离散，在处理区间端点值的逼近时，为避免数值振荡而使其保持迎风特性，并提出一种新的方法使格式精度整体提高到二阶. 该方法在上游单元中心处作泰勒级数展开，通过相关辅助未知量以完成梯度的重构，并对出负情形作正性校正，使得格式满足保正性要求.

该格式只含有区间单元中心未知量，并满足区间端点处通量的局部守恒性. 数值实验表明，本文格式对于处理扩散占优、对流占优问题，扩散系数连续和间断情形均具有良好的适应性，并保持二阶精度；并且，当网格退化为等距网格时，计算精度并未受到影响，这表明本文格式不受网格限制，可进行任意非等距网格剖分.