多源柔性电网灾变恢复智慧预案优化评估
2021-01-09蔡振华陈东海房鑫炎李亦凡
蔡振华,陈东海,金 力,房鑫炎,李亦凡
(1.国网浙江省电力有限公司宁波供电公司,浙江 宁波 315000;2.上海交通大学电子信息与电气工程学院,上海 200240)
0 引言
近年来,随着各种电力新技术的发展,电网可再生能源渗透率逐渐提高,交直流混联电网多模式运行,特高压受端电网受电率不断提高,短路比不断下降。相较于传统电网,当下电力系统的拓扑结构更加复杂,其稳定性受到了一定程度的影响。这种电网运行方式会带来诸如特高压换流站换相失败、电力电子设备谐波干扰、柔直异步并网等新的安全隐患问题,更容易导致电网大面积停电等灾变事故的发生,造成更大的经济损失与更广泛的社会影响。
灾变恢复智慧预案作为电力系统应对大面积停电事故的主要措施之一,具有重要的研究和实用意义。目前对电网的灾变恢复预案体系已经有大量研究。文献[1]通过对电网应急能力进行时空维度的拆解,构建了电力系统灾变恢复的动态评价指标体系,实现了对文献[2]中的静态指标体系的补充。文献[3-4]对配电网应对极端灾变的恢复力指标进行了研究,使电网对发生概率小但是破坏性大的极端事件有更好的应对能力,是对小概率情况下电网灾变恢复预案的补充。在指标体系建立和算法研究方面,文献[5]提出D-AHP(基于D 数理论的层次分析法)作为降低专家主观性的方法。文献[6]通过主、客观赋权结合的方法,提高了赋权的客观性。文献[7]提出结合TOPSIS(逼近理想解排序法)与直觉模糊熵的评估模型,根据决策者的风险系数进行调整,可靠性更高。但这些预案的有效性和可行性都不高,其主要原因可以归纳为:基于事件触发的预案流程时间尺度的单一性、滚动预案的静态特性、预案执行的可用资源的局限性。
综上所述,当前对电网灾变恢复预案的研究存在不足之处。本文针对多源融合的柔性电网特征,结合态势感知技术,完善预案的关联性和有效评估,以实现真正意义上的智慧恢复预案,主要包括:多源支撑的源网荷储协调机制;基于多时间尺度的预案动态特性;出力特性及负荷特性的高匹配度;能量路由器及能源物联网的应用。
本文在传统电网灾变恢复预案评估体系的基础上,增加针对新型电网特色的分层指标,建立在多馈入的新型电网结构下,电力系统灾变恢复预案的动态评价指标体系。采用D-AHP 与Poisson 分布对各级指标和时间序列的权重进行赋值,采用TOPSIS 计算各项指标的评估结果与实时数据的欧氏距离和贴近度。最后,以某一区域电网下不同灾变恢复预案的对比评估作为仿真算例,对本文所提灾变恢复预案的评估体系以及模型算法的有效性与可行性进行验证。
1 多源柔性电网灾变恢复智慧预案评价指标体系
1.1 时间维度分解
电力系统灾变恢复预案通过基于时间维度的阶段划分获得动态指标。根据灾变情况的发展过程,电力系统的运行状态可以分为以下几个阶段(见图1):正常运行阶段,0<t<t1,t>t3;灾变阶段,t1<t<t2;灾变恢复阶段,t2<t<t3。

图1 灾变过程时间维度
每个阶段,电力系统对灾变的评判指标不是一成不变的,不同时期每个指标的权重应该不同。以电力系统灾变恢复能力作为零级指标,从时间维度对整个过程进行拆解,将灾变前预防阶段的控制能力、灾变发展阶段的严重度、灾变恢复阶段的恢复力作为评价指标体系的一级指标,同时也作为本文评价指标体系的时间序列。
1.2 多源柔性电网的灾变恢复智慧预案
随着电力技术和通信技术的快速发展,传统电网已经逐渐被新型的多源柔性电网所取代,灾变恢复预案也逐渐变得智能化。
(1)随着电网的新能源渗透率提高,配电网结构从传统的单向潮流辐射式电网变成了多向潮流的多源融合新型电网,多源接入给区域电网的灾变恢复带来了巨大影响。在灾变恢复过程中除了考虑传统的网架重构与负荷恢复以外,还需要协调支撑电源与网架、负荷之间的功率匹配问题,以“源网荷储”作为协调机制统筹规划。同时,分布式能源的功率预测水平也是决定灾变恢复调度预案准确性的关键因素之一。
(2)特高压交直流混联工程的投入,使得特高压受端电网的受电比例不断提高,对特高压直流逆变站的故障监测措施能够保障特高压受端电网的电能稳定。
(3)能量路由器作为能源互联网实现协调调度的控制单元,获得了广泛的应用。其基于电力电子设备实时通信的控制方式,使得电网的调度指令传递速度获得了巨大提升。在电网灾变恢复预案的评估中,能量路由器的控制力能够很大程度影响电网灾变恢复能力。
(4)大数据和5G 通信时代下,新型电网的数据量大幅上升,电网对数据的处理分析能力将很大程度上影响灾变恢复过程中决策判断的速度与准确性。基于大数据分析、人工智能手段以及5G通信技术的智慧型预案将取代传统恢复预案,成为主要的灾变恢复预案体系。
1.3 新型柔性电网的灾变恢复智慧预案评价指标体系
综上分析,可以形成如表1 所示的新型柔性电网灾变恢复预案评价指标体系。
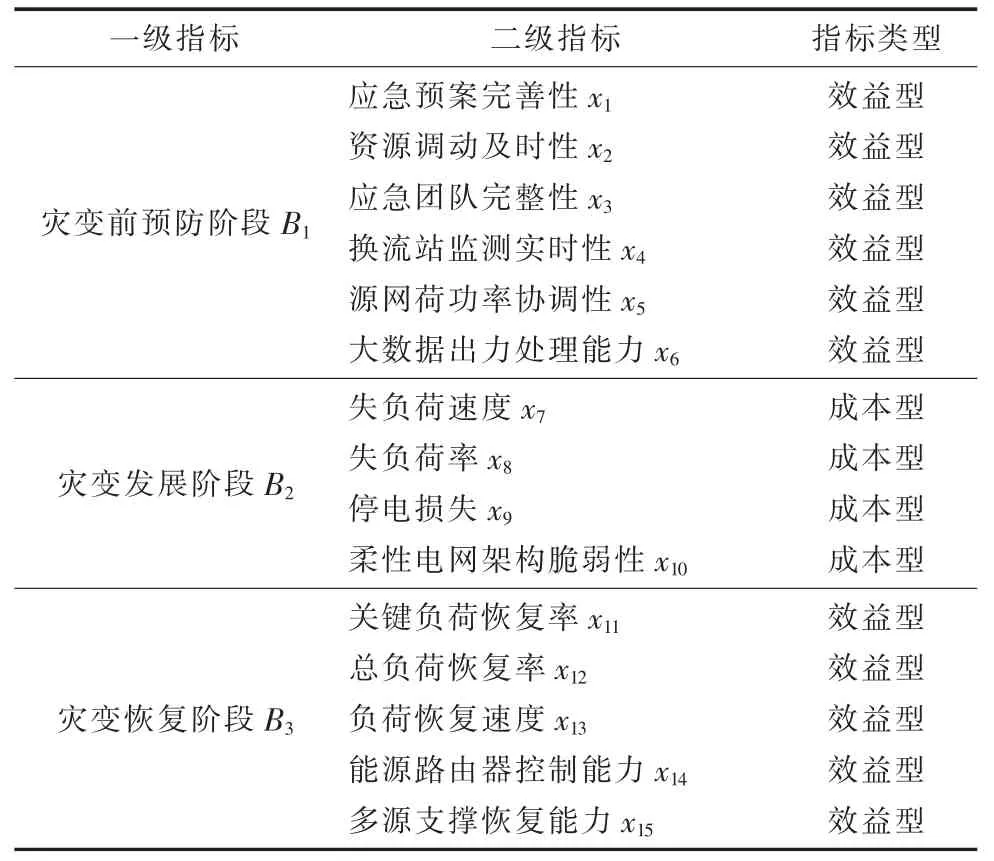
表1 新型电网灾变恢复预案评价指标体系
2 综合权重模型
2.1 D-AHP
D-AHP 是基于D 数理论对AHP 进行改进的一种分析方法[5]。D 数理论继承了D-S 证据理论在处理不确定性信息方面的优势,并且能够处理信息不完整的情况,具备更大的应用范围,已经在不同领域广泛应用。关于D 数的定义见文献[8]。
D-AHP 在传统AHP 的基础上,通过D 数偏好关系求解指标权重,对存在不确定信息的主观评价体系进行求解,有效降低评估过程中的专家评价主观性对结果的不利影响。本文构建的电力系统灾变评价体系层次结构模型如图2 所示。
D-AHP 计算指标权重步骤如下:
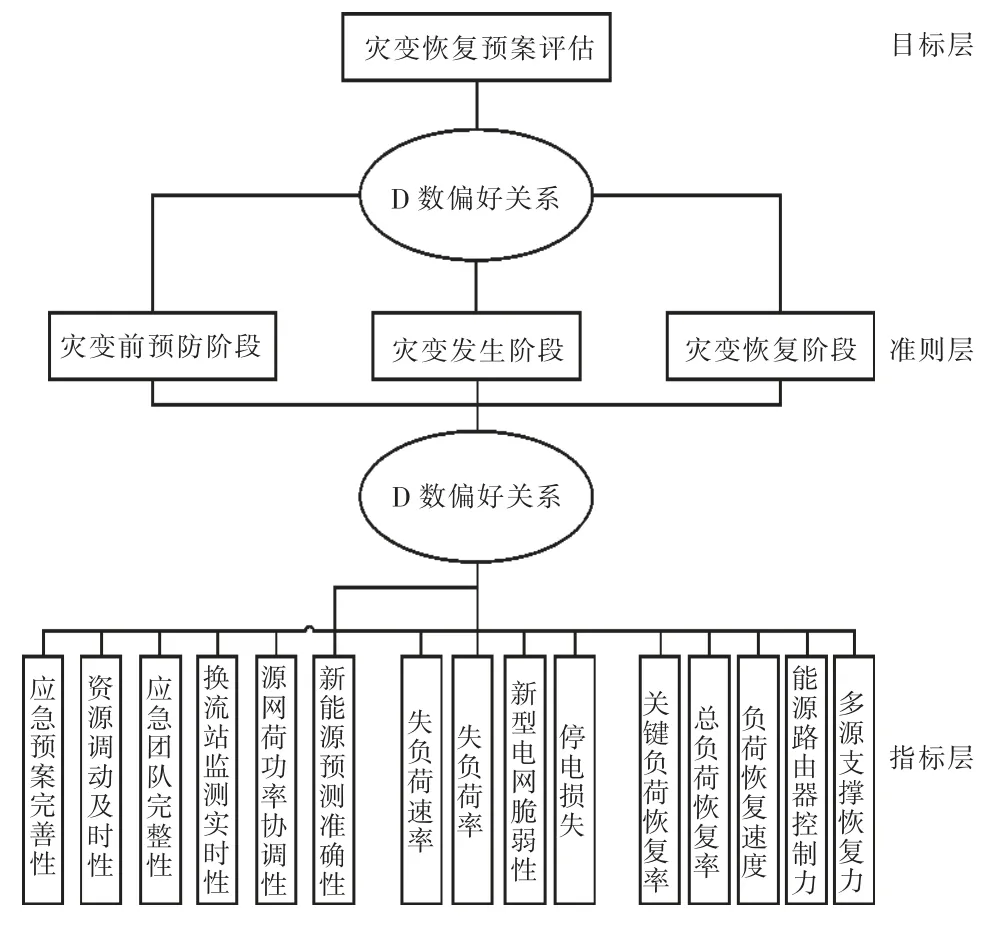
图2 灾变恢复预案评价体系层次结构模型
Step1,专家们对指标进行成对比较评价,以偏好关系表达对各个指标的重要程度,构建D 数偏好矩阵RD。
Step2,利用公式将D 数偏好矩阵RD转化为实数矩阵RC。
Step3,构建基于实数矩阵RC的概率矩阵RP[8]。
Step4,计算概率矩阵RP中每行的和并按大小排序,根据矩阵排序得到三角化矩阵。
Step6,计算各指标的相对权重。
在计算权重时,不一致系数为:

式中:n 为成对比较的指标个数。D-AHP 的不一致系数常见取值范围为小于0.1。
2.2 Poisson 分布确定时间权重
电力系统灾变是一个动态循环的过程,想要对整个系统灾变状态进行全面客观的评估,就要将时间序列赋予一定权重,纳入考虑因素。所赋予的权重应具有以下特征:
(1)权重序列应该是一个离散序列,可以根据时间序列进行调整。
(2)对于每个阶段来说,当前阶段的重要程度显然更高,并且在当前阶段之后的阶段比当前阶段之前的阶段更重要。
(3)权重之和为1。
文献[9]通过主观法定义时间权重,该方法主观性过高,且不够准确。文献[10]中TOWA(时序加权平均算子)与TOWGA(时序加权几何平均算子)的时间序列权重赋值办法采用专家评判指标,同样具有主观性强的缺点。Poisson 分布是概率学中用于描述单位时间内随机事件发生次数的一种方法,在现实生活中大多数情况都服从于Poisson分布。本文中采用Poisson 分布的正态函数对时间权重进行赋值,相比于主观法赋值,它有更好的通用性与准确性。因为电力系统灾变是一个动态循环的过程,定义a3为与当前电力系统阶段最为接近的时间序列,例如研究电力系统灾变恢复预案时,预防状态为时间序列a3,灾变阶段为a1,恢复阶段为a2。
权重η 计算公式为:
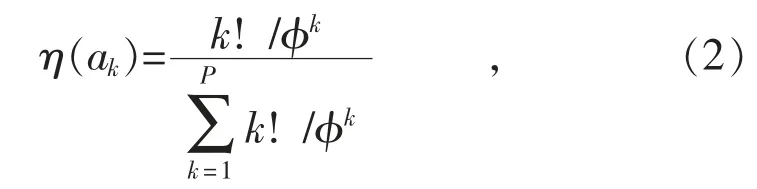
2.3 TOPSIS[5]
TOPSIS 是一种常用的综合评价方法,可充分利用原始数据的信息,其结果能精确反映各评价方案之间的差距。
TOPSIS 的一般步骤如下:
Step1,专家组h={h1,h2,…,hm}评判指标集U={U1,U2,…,Un},获得初始评判矩阵MA=[aij]m×n,即

Step2,将初始评判矩阵中所有指标aij转化为极大型指标bij,即指标正向化。
对于极大(效益)型指标:
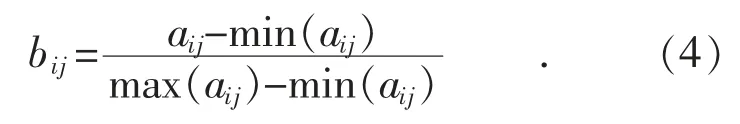
对于极小(成本)型指标:
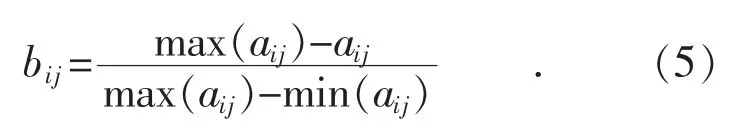
由此,可获得标准化矩阵MA=[aij]m×n,MB=[bij]m×n。
Step3,构建加权后的标准化矩阵,即将评价指标与标准化矩阵MB的指标实际数值对应相乘,获得加权矩阵MC=[cij]m×n。
Step4,定义最优解和最劣解,并计算欧氏距离,确定最优方案和最劣方案。
定义最大值:
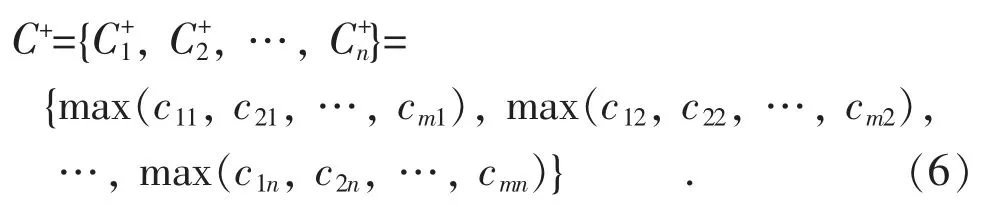
定义最小值:


Step5,计算每个样本未归一化的得分,然后完成对每个样本的优劣排序,最后进行归一化处理:

3 算例验证分析
为了验证本文所提的评价指标体系能够有效评估新型多源柔性电网的灾变恢复智能预案,以某个具备新型多源柔性电网结构的区域电网作为算例,针对A,B,C 3 种恢复预案,采用本文所提评价指标体系进行评估分析,各指标评估情况见表3。
方案A:该区域电网十几年前的传统电网灾变恢复预案。此灾变恢复预案针对的是十几年前的传统电网,当时的电网没有大数据与智能化,也没有多源柔性电网的结构特征,因此该方案在传统性指标{x1,x2,x3,x7,x8,x9,x11,x12,x13}方面的评估结果较好,在多源柔性电网以及大数据智慧预案指标{x4,x5,x6,x10,x14,x15}方面的评估结果较差,或者几乎处于空白状态。
方案B:该区域电网数年前的多源柔性电网灾变恢复预案。由于电力技术的进步与电网要求的提高,方案B 比方案A 在传统性指标{x1,x2,x3,x7,x8,x9,x11,x12,x13}方面的评估结果有少许提升,在多源柔性电网指标{x4,x5,x10,x15}方面的评估结果较好,在大数据与智能化指标{x6,x14}方面的评估结果较差。
方案C:该区域电网当代的新型多源柔性电网灾变恢复智慧预案。相比于方案A 和方案B,方案C 在本文构建的评估体系中各项指标均表现优越。
具体步骤如下:
(1)D-AHP 层次结构构建。
构建D-AHP 层次结构模型,如图3 所示。
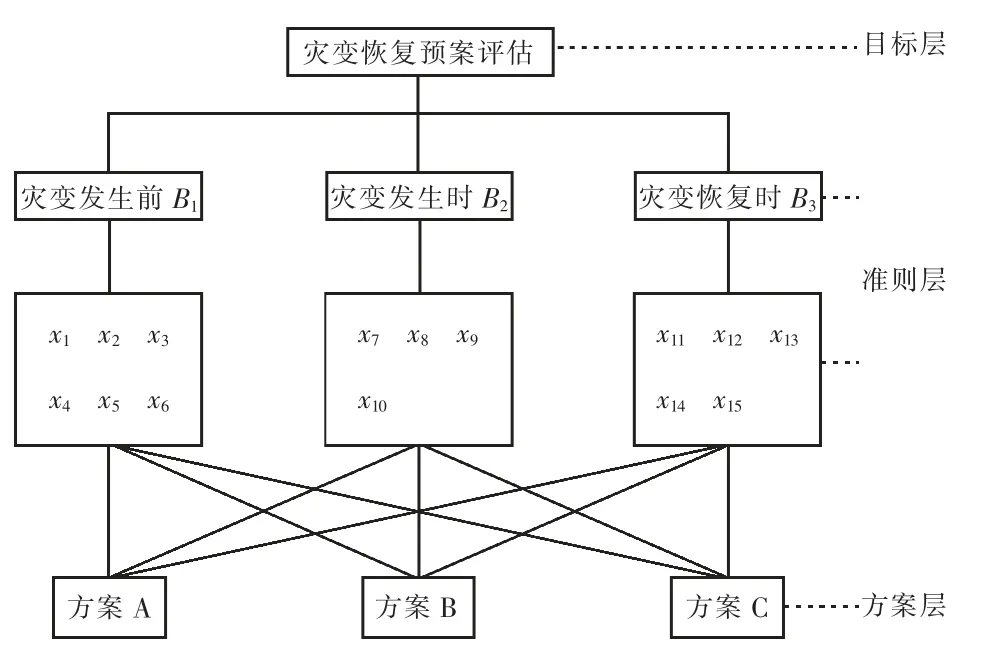
图3 D-AHP 层次结构模型
(2)D-AHP 权重计算。
邀请电力系统灾变领域研究可信度较高的10 位专家为本文的所有指标两两打分比较。使用D数理论对专家信息进行汇总,获得D 数偏好矩阵RD,矩阵和求解过程见附录A。
同理,二级指标相对于准则层一级指标的权重也可以通过D-AHP 求得,具体步骤同准则层一级指标,本文中不再赘述。计算结果见表2。

表2 各指标权重数值
(3)时间权重计算。
根据时间序列的Poisson 分布求得{a1,a2,a3}的权重为={0.200 0,0.266 7,0.533 3},选取φ=1.5。在灾变预防阶段,即预防阶段为时间序列a3,灾变阶段为a1,灾变恢复段为a2。经过时间序列权重与D-AHP 获得的一级指标权重线性加权,标准化处理以后,得到一级指标权重={0.518 8,0.288 7,0.192 5}。
(4)应用TOPSIS 进行排序。
根据本文的指标体系,组织专家对方案层3个方案的定性指标进行评估打分,通过SCADA系统统计定量指标,并统一标准化处理为区间[0,1]的数据,如表3 所示。
对各项指标结合表2 的综合权重进行加权,取处理后的各项指标最大、最小值分别作为正、负理想解,根据TOPSIS 计算公式,得到如表4所示的欧氏距离和贴近度。

表3 各方案的指标评估打分
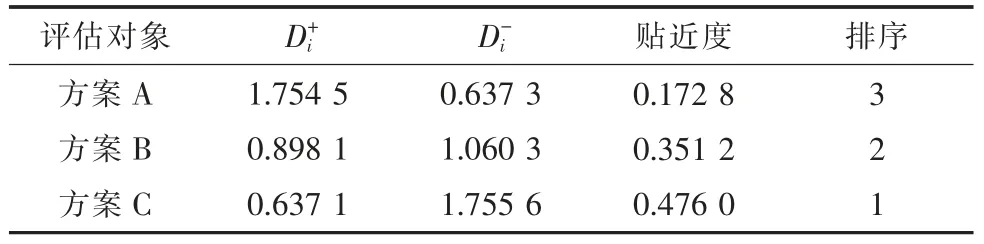
表4 各方案的欧氏距离和贴近度
由表4 的计算结果可以得出结论:对于该区域电网,A,B,C 3 个灾变恢复预案对比结果为C>B>A。本文所提的评价指标体系能够评判灾变恢复预案对新型电网的适用性,能够对新型电网下的灾变恢复智慧预案作出全面的评估,对新型电网的灾变恢复智慧预案有指导性作用。
为了验证本文所提的基于D-AHP 与Poisson分布确定指标专家权重与时间权重的综合指标建模方法的科学性与优越性,应用传统AHP 建立指标权重模型与本文方法进行分析对比,指标权重计算结果如图4 所示。
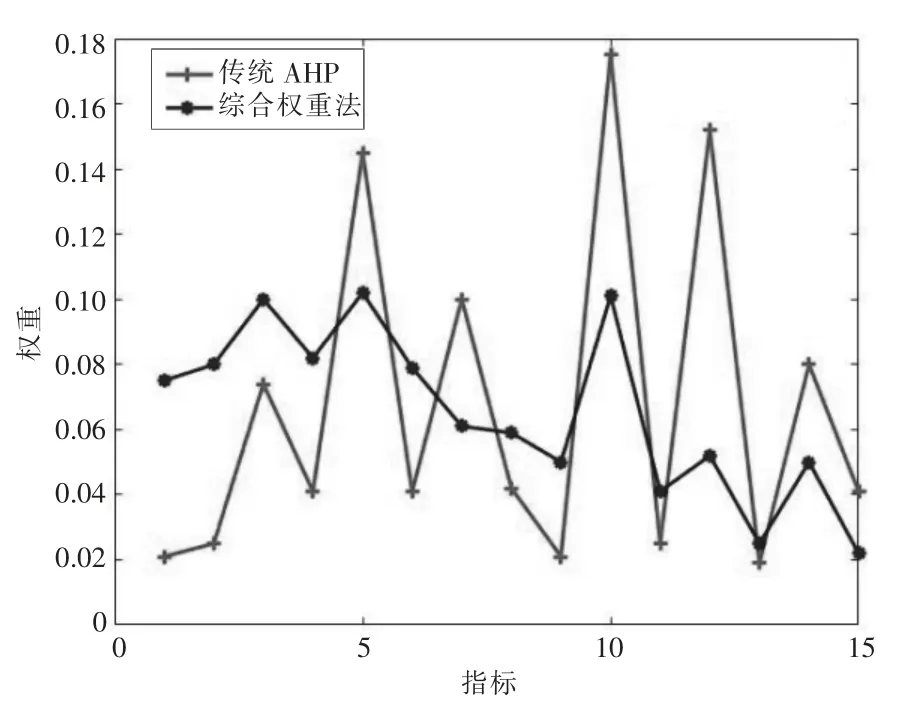
图4 本文方法与传统AHP 指标权重对比
根据图4 的指标权重曲线可知,传统AHP指标权重的波动明显偏大,专家主观性强,而本文所提综合权重法得到的指标权重更加平均,专家主观性被最大程度地降低。同时,时间权重的加入使得综合权重指标在灾变预防时期的指标权重更大,符合本文所提时间权重指标存在的意义,更加符合实际情况。采用TOPSIS 对AHP 确定的指标权重的各方案进行计算,各方案欧氏距离和贴近度排序结果为C>B>A,与本文所提方法的结论相同,证明了本文所提方法的科学性。
4 结语
本文针对传统灾变恢复预案无法适应新型电网的问题,在传统的恢复预案评价指标体系的基础上,综合分析新型多源柔性电网、灾变恢复智慧预案,增加了新型电网的特征指标,并提出了一种结合D-AHP 专家评估权重和Poisson 分布的正态时间权重的动态评估模型,采用TOPSIS求解。算例结果表明,本文建立的多源柔性电网灾变恢复智慧预案评价体系能够适应当前的多馈入新型电网结构下的灾变恢复智慧预案,具有较大的现实意义。对比传统赋权法,本文所提综合权重赋值法的结果具有主观性减弱、更符合实际时间分布的优势。
附录A


B1B2B3每行的和

根据概率矩阵RP可以对各指标排序B2≻B1≻B3,获得对灾变状态的评估结果影响程度由高到底依次为灾变的严重程度,灾变发生前应急预防,灾变恢复能力。


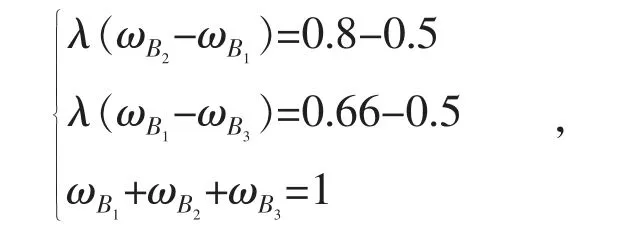
式中:λ 为信息可信度[12];为第i 个一级指标的权重。因为专家可信度足够高,令λ=2,由此得到指标权重取值为:=0.31,=0.46,=0.23,与从概率矩阵得出的指标重要度排序吻合。
