基于宽负荷调峰技术的电网频率弹性提升方法研究

李云鹏，杨秦敏，张志祥，徐 石

（1.浙江大学 控制科学与工程学院，杭州 310027；2.国网浙江省电力有限公司杭州供电有限公司，杭州 311300；3.杭州电力设备制造有限公司，杭州 311300）

0 引言

电力是现代工业社会经济的发展动力和物质基础，能源类型及其使用方式的革新深刻影响着人类[1]。因此，电力基础设施在源、网、荷、储各个环节都需要安全、稳定、高效地运行与管理，以保障医疗、通信、运输等关键部门的电力供应[2]。然而，中国广袤的国土面积和多变的地理环境客观上促成了目前“集中式生产、远距离传输”大电网的现状[3]，电网频繁受到自然灾害影响，具有一定的脆弱性。另一方面，随着可再生能源的大规模并网，风能、光能、潮汐能、地热能等可再生能源固有的随机特性和间歇特性在加剧了电网频率波动的同时也增加了电网的脆弱性，严重阻碍了高质量可再生能源及时消纳[4]。因此，为了保证电网逐步向互动、自愈、高安全性与高可靠性发展[5]，电网弹性提升技术的研究受到学术界越来越多的关注[2，4-8]。

1 研究现状

1.1 电网弹性提升技术研究现状

“弹性电网”的提出和发展为电网电气参数稳定性和恢复力提供了科学的理论框架和参考[9]。学术界引用“弹性”的概念来衡量电力系统应对突发灾害的抵抗能力和恢复能力。现有文献中，为了实现电网弹性的有效提升，学者们分别在源、网、荷、储等环节开展深入研究，提出了多种技术解决方案。

文献[2，10-12]系统地研究电网的弹性评估问题，完成了电网脆弱性以及恢复过程的建模并结合模型进行电网弹性评估和优化。在文献[13]中，一种参数化的控制框架被提出以实现同步发电机在电网偶发极端情况中的稳定控制。文献[8]则通过添加冗余线路、断路器、发电机和变压器并建立了一种易于处理的模型以优化改善电力输送系统。相应地，在文献[14]中，提出了一类分布式多智能体微电网，用分布式发电策略提高弹性电力系统的自愈能力。文献[15]设计了一种包含抽水蓄能机组参与的主动发电控制方法，通过调整切换蓄能电站的工作状态实现机组输出功率的阶跃变化。这一方案使得抽水蓄能机组与火力发电燃煤机组能够共同参与系统的频率控制，提高了电网频率的弹性。文献[16]研究了微电网与分布式电源在配电网的弹性指标与提升方法，提高了配电网在极端事故下的弹性。文献[17]研究了微网在孤岛模式下，电源供电中断时引入超级电容等快速储能设备以缓解孤岛电网频率骤然下降，减少低频低载次数。此外，运用电价交易手段[18-20]来引导用户用电行为，拓展可控负荷类型和规模进而抑制尖峰负荷产生也作为一种支撑电网弹性的方式被广泛研究。

虽然上述技术方案均可在一定程度上改善电网频率弹性，但随着可再生能源并网比例进一步提高，系统仍将面临频率波动特性大、动态电气参数下降、调频容量不足等问题。结合我国现有能源秉性以及燃煤发电机组的可观储量，选择从发电源头端改进提高燃煤发电机组的负荷响应速度及范围，以缓解消纳高弹性电网中大规模可再生能源接入可能导致的频率波动特性大以及动态电气参数特性下降等问题，具有现实意义及研究价值。

1.2 燃煤机组调峰控制研究现状

就燃煤机组调峰技术而言，协同控制系统的控制是调节负荷的关键，其在现有研究中的控制算法大致可分为两类：

第一类是以传统PID 控制算法及基于PID 的衍生线性算法，包括串级PID[21]、模糊PID[22]、基于内模的PID[23]等，实现了较好的控制性能，但抗干扰能力较弱。随着机组调峰负荷指令跨度增大时效性要求提高，缓慢且不稳定的机组输出功率调节无法缓解可再生能源随机性给电网带来的负面影响。

第二类是以先进控制理论为基础的非线性控制算法，包括鲁棒控制[24]、基于无源控制理论的控制[25]、预测控制[26]、自适应控制[27]等。这类算法虽然一定程度上改善了协同控制系统的负荷响应性能，但就大范围快速的负荷响应而言，无法保证在预设收敛时间内快速稳定。因此，为了进一步提高负荷响应速度进而提升电网频率弹性，需要设计预设系统性能的先进控制算法。

2 控制系统建模

2.1 超超临界燃煤发电机组非线性模型

为更加符合真实燃煤机组工作状态，引入一个多输入、多输出耦合非线性系统模型[28]设计控制器，其机组建模结构如图1 所示。

对机组建模得到三阶非线性系统[28]：

图1 燃煤发电机组建模

式中：c0，c1，c2，j1，j2，l，hfw为系统已知参数；k0，k2为系统未知参数；x1为进入直流锅炉的实际煤量；x2为汽水分离器出口的蒸汽压力值；x3为汽水分离器出口的蒸汽热焓值。

超超临界直流炉汽轮机系统的3 个控制输入分别为：u1为磨煤机给煤指令；u2为总给水量；u3为汽轮机阀门开度。此外，状态空间表达式中的函数为：f（v）=43.22v-31.84，g（v）=0.13v0.882，h（v）=-8.96v+3 717.4。系统输出可描述为：

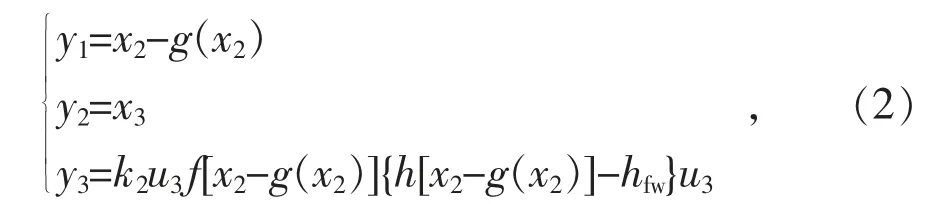
式中：y1为主蒸汽压力；y2为主蒸汽热焓；y3为汽轮机输出功率。

2.2 控制目标

为保证负荷响应稳定性和时效性，所设计控制算法需实现：燃煤机组控制系统各个输出稳定有界，且最终收敛至期望值附近的紧集，即yi→yid，i=1，2，3；燃煤机组各个输出在预设时间Ti，i=1，2，3 内收敛。

3 控制器设计

3.1 模型反馈线性化

定义如下标识符号：b1=1/c0，b2=（hfw-j1）/c1，b3=（hfw-j2）/c2，θ1=k0/c0，θ2=k0/c2，θ3=k2。

使用状态变量拓张技术，令：

结合式（1），（2）和（3），将系统改写为：

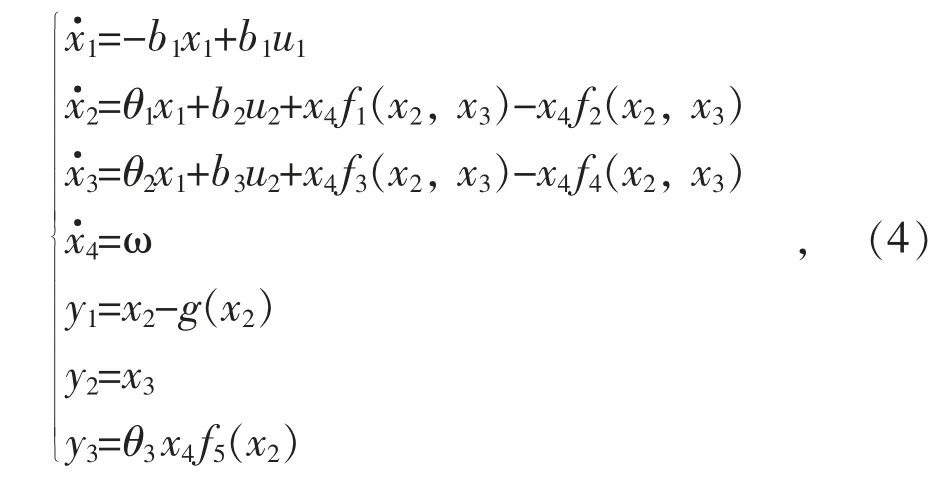
其中

运用反馈线性化技术将系统动态模型转化为精确线性化模型：

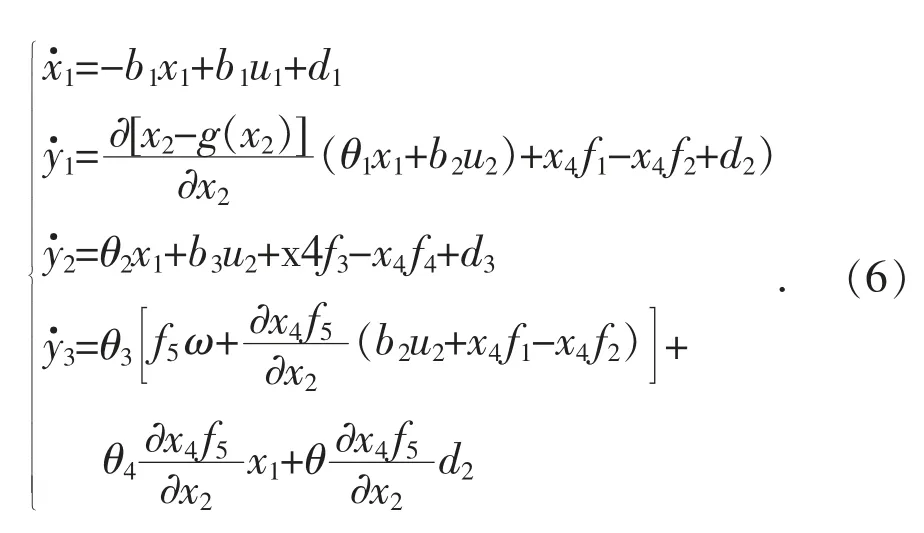
3.2 预设时间收敛的控制算法设计

设定系统控制目标值并定义跟踪误差。定义为y1d主蒸汽压力设定值；y2d为主蒸汽热焓期望值；y3d为汽轮机功率期望值。定义e1=y1-y1d为主蒸汽压力跟踪误差；e2=y2-y2d为主蒸汽热焓跟踪误差；e3=y3-y3d为汽轮机功率跟踪误差。

设计预设时间快速稳定时间轨迹函数μi（t），i=1，2，3，4，表示为：

式中：Ti，i=1，2，3，4 为预设时间。

对其求导可得：

设计中间转换函数wi（t），表示为：

对其进一步求导可得：

设计一类时变非线性K 类函数Ψi（x），i=1，2，3，4 满足：

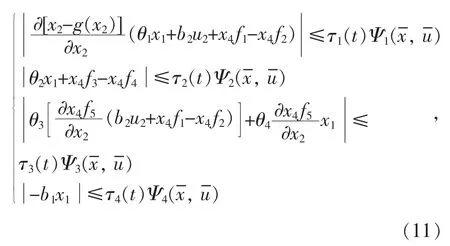
式中：τi为未知有界结构不确定性系数；Ψi为待定连续正定函数，且=x1，x2，x3，=u1，u2，u3。实际控制器中选择：

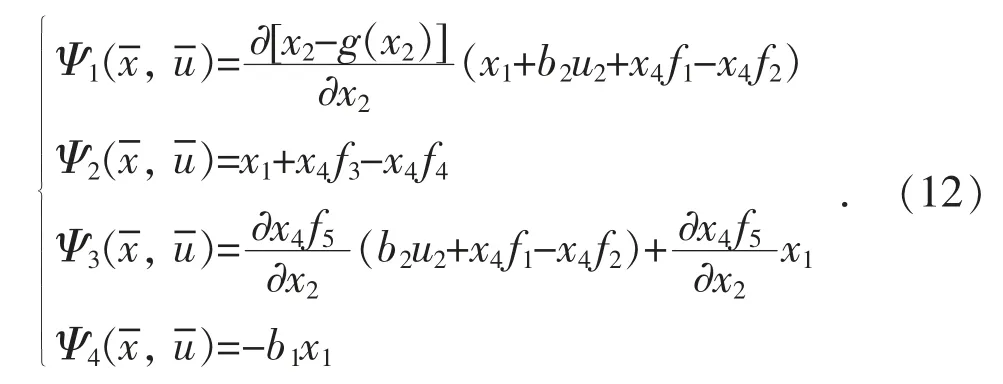
首先对机组中的给水指令u2和阀门开度u3设计预设时间内快速稳定的超超临界燃煤机组自适应控制器为：

式中：kc2，kc3，λ2，λ3为可调控制增益。

接着对机组给煤指令设计控制器，注意到变量x1，y1的动态可组成严格状态反馈系统，因此用反步法分别设计虚拟控制率α1和实际控制信号u1。令e4=x1-α1，得到：

式中：kc1，kc4，λ1，λ4为可调控制增益；Ti，i=1，2，3，4 为预设收敛时间；mi，i=1，2，3，4 为可调时间函数轨迹参数。

类似于文献[29]，根据李亚普诺夫稳定性理论，对机组各个输出选择李雅普诺夫函数，i=1，2，3，4，即可定量证明，i=1，2，3，4，并且机组闭环系统的信号有界。最后，所设计控制器逻辑如图2 所示。

4 仿真分析

通过在MATLAB 中搭建的机组仿真模型，验证所提预设收敛时间的自适应控制算法的有效性。为更加贴近机组真实工作状态，分别在x1，x2，x3的动态中加入连续时变干扰d1，d2，d3。不同负荷段为0＜t＜100；d1=d2=d3=0；100≤t＜300；d1=0.001sin0.1t，d2=0.002sin0.1t，d3=0.03sin0.1t；300≤t＜500；d1=0.01sin0.1t，d2=0.05sin0.1t，d3=0.03sin0.1t。设定机组按照阶跃负荷指令先从720 MW 上升至850 MW，再上升至930 MW。机组在初始零时刻y1（0）=20.6，y2（0）=2 712，y3（0）=720。在仿真模型中涉及的燃煤机组参数见表1。

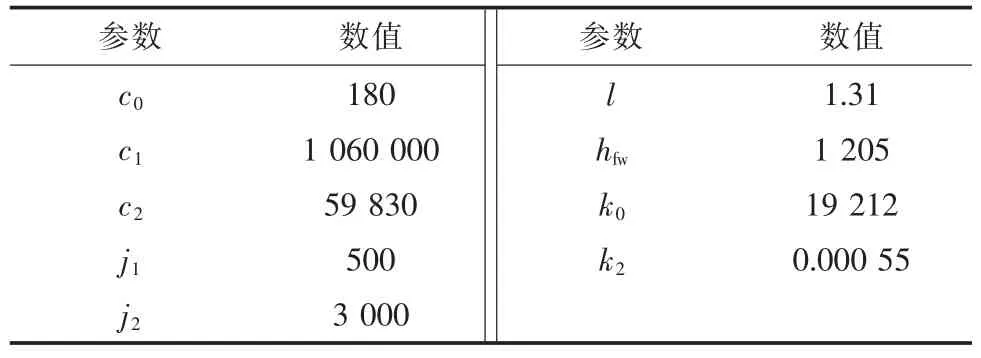
表1 燃煤机组系统参数

仿真验证了所提预设时间快速收敛的自适应控制器可保证燃煤机组各个输出的稳定控制，不仅对建模精度的要求进一步降低，且可抵抗一定的非结构性不确定性。为了进一步验证所提算法在预设时间收敛以及抵抗干扰方面的优越性，增加传统的基于模型的FL（反馈线性化控制）[30]以及PID 算法作为对比，各控制器增益见表2。图3为机组输出的负荷响应对比，图4 是机组实际状态变量对比，图5 是跟踪误差对比。从仿真结果中看出由于PID 算法不基于系统模型仅根据误差设计，在对多变量耦合的复杂多输入、多输出系统中的控制效果最差，在瞬态响应初期甚至反方向调节造成超调量进一步增大。并且抵抗外部干扰的能力较差。对于基于模型的FL 算法而言，虽然其控制精确度得到提高，但是依然无法实现较好的干扰抵抗效果及预设时间内收敛。然而，在本文所设计控制算法作用下，机组可在系统部分动态参数未知且存在外部干扰的情况下快速地对大范围阶跃变负荷指令的工况下实现高精度稳定输出控制。机组各状态变量及输出变量有界稳定，既保证了变负荷工况的控制效果，又能在规定的预设时间内收敛，提升负荷响应精度和对电网负荷指令响应的时效性，进而提升电网弹性。

图2 控制器框图

表2 控制器增益

图3 机组变负荷输出响应

图4 机组变负荷状态变量响应

图5 机组变负荷输出跟踪误差

为进一步分析电网频率弹性的提升，结合文献[30]中所用同步发电机简化模型分析机组输出功率快速响应对电网频率的改善。引入=k（PMPE-PL），其中fg表示电网频率，k=9.615 385×10-11为发电机固有参数，PM，PE，PL分别表示总电机机械功出力，电网总耗电功率和由于灾害、故障导致的部分可再生能源发电端发电出力。假设由于灾害或故障导致电网频率瞬时下降至59.5 Hz，故障造成PL=65 MW。故障发生后电网立即下达指令要求火力发电端立即以130 MW 功率增量补偿直至频率恢复正常。机组面临的外界干扰及参数选择与之前仿真相同，得出不同机组控制算法下电网频率变化对比曲线如图6 所示。相较于传统反馈线性化算法和PID 算法，所提算法在105 s附近即可恢复至额定功率，而相同时间内其它对比算法由于功率补偿不充分并不能及时提升电网频率。相同条件电网频率的弹性得到有效提升。

5 结论

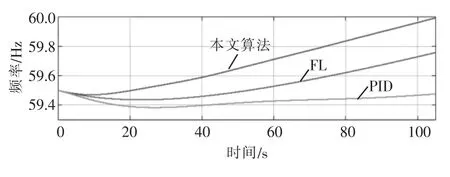
图6 频率响应对比

为改善大规模可再生能源接入下电网频率的弹性，本文针对超超临界燃煤机组协同控制系统设计了一种可预设收敛时间的自适应控制算法实现机组快速变负荷指令下的精确调峰。仿真对比结果验证了机组输出功率可在预设时间内精确响应调峰负荷指令并具有抵抗外界干扰的能力。随后结合简化电力系统频率模型验证了电网频率弹性得到有效提升。