黄土路基补强分层压实度检测方法

2021-01-09周志军张志鹏郭涛徐天宇

铁道科学与工程学报 2020年12期

周志军, 2，张志鹏，郭涛，徐天宇

黄土路基补强分层压实度检测方法

周志军1, 2，张志鹏1，郭涛3，徐天宇1

(1. 长安大学公路学院，陕西西安 710064；2. 西安长大公路工程检测中心，陕西西安 710064；3. 中土集团福州勘察设计研究院有限公司，福建福州 350013)

为了快速有效地检测路基分层压实度，以黄土路基为例，提出通过液压夯实机的夯击补强作用来检测路基分层压实度的思路。基于分层压实理论，建立液压夯实的基本模型并推导了夯前和夯后分层压实度的关系，设计并开展液压夯实足尺模型试验。研究结果表明：深度超过约1.5 m时，压实效果可以忽略；路基分层界面沉降量和表层夯沉量具有阶段性变化特征，分别以0.8～1.2 m和6～9击为界限。引入有效压实深度的概念并建立其回归公式；采用回归方法得到了表层夯沉量、有效压实深度和分层界面沉降量之间的玻尔兹曼函数关系；采用线性回归方法得到了夯后分层压实度与分层界面沉降量及表层夯沉量之间的关系；推导出夯前路基分层压实度计算公式，形成了黄土路基补强分层压实度检测方法。将液压夯实法运用于实体工程，其计算结果和灌砂法检测结果的误差在2%以内。

道路工程；黄土路基；液压夯实法；模型试验；有效压实深度

黄土广泛分布于世界各地，约占全球陆地面积的10%[1]。黄土具有疏松、湿陷的特性，因此需要严格控制黄土地区路基质量[2]。而路基压实度是评价路基质量的重要参数，直接关系到路基的工作性能和使用寿命[3]。因此，对路基压实度的控制和检测具有重要意义。目前我国常用的压实度检测方法包括环刀法、灌砂法、灌水法等，均是采用简单的等效原理，将土体的特征参数与标准物质进行换算，进而获得简单直观的测量数据，从而计算压实度的基本数据以得到压实度值[4]。这些方法简单高效，经过了长期的发展与实践。但是随着公路施工技术的不断发展，对压实度的控制愈发严格，现有的现场检测压实度的方法存在许多的问题与不足，如可靠性差、检测费时费力、成本高等问题，且检测局限于路基表层，无法检测分层压实度，已不能满足快速发展的交通土建工程的需求。因此，需要研究新的路基压实度检测技术。液压夯实机自1990年由英国BSP公司成功研发[5]，经过近30 年的发展，在旧路基改扩建夯实补强、建筑垃圾路基填筑补强、三背路基夯实补强及路面表层微裂破碎等方面得到了广泛应用，形成了较完整的液压夯实法加固补强路基的体系[6−12]。司癸卯等[13]对液压夯实机的压实效果和影响范围进行了研究；刘本学等[14]基于动力碰撞理论对液压夯实机的作用机理进行了分析研究；冯雄辉等[15]基于ADINA有限元分析软件建立了不同深度下液压夯实机处理高速公路台背的模型，认为夯实作用区域的应力呈“八”字型向下传播。相关研究成果对于工程的建设具有重要参考意义，但研究方向多局限于路基补强，对液压夯实机的夯实效果研究不够深入全面，缺乏指导实际工程的理论方法。本文通过室内足尺模型试验，分析液压夯实作用下黄土路基各物理力学参数的变化，建立土体特征参数的联系，确定各计算参数值，形成了通过液压夯实法检测黄土路基压实度的体系，为黄土地区的路基压实度检测提供了参考和指导。

1 分层压实理论

假定夯击过程中，一定深度范围Δ内的土体被压实，含水率保持不变且接近最佳含水率，建立如图1所示基本模型。经压实后土体压缩量为Δ。由于土体发生侧向挤出，实际压缩量小于Δ，因此引入修正系数，将土体实际压缩量表示为Δ。的值介于0～1之间，并随着深度变化而变化。

根据路基压实度定义和土的干密度定义[16]，有：

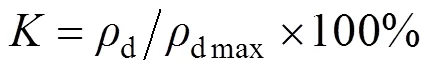
式中：为路基压实度；d为土的干密度；s是土粒质量；dmax为土的最大干密度；为土体体积。

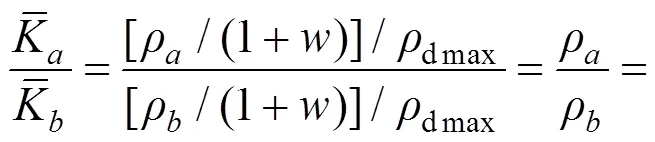
(3)

将路基按每土层厚度为进行分层，将每层土体从上向下依次编号为0，1，2，3，…，，如图2(a)所示。则每分层土体上层界面深度=，下层界面深度=(+1)，=0，1，2，3，…。夯击之后，如图2(b)所示，上层界面深度变为i+s，下层界面深度变为(+1)+(i+1)d，s为分层界面处的沉降量。夯前土层厚度Δ=，夯后土层厚度Δ1为下层界面深度与上层界面深度之差，即：

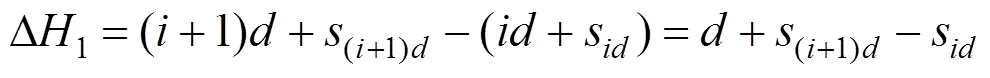
则土层压缩量为

联立式(3)，取Δ=即可得到：

为了探究夯击前后黄土物理指标的变化情况并获取相关参数，本文进行了足尺模型试验，探究液压夯实机夯击作用下各个试验指标的变化规律与相互关系，从而完善路基补强分层压实度检测方法。

2 试验设计与方法

2.1 土样基本物性

试验用黄土土粒细小，含少量粉土和黏土，大部分粒径在0.074～0.25 mm之间。土质均匀，结构疏松，含水率低，含有少量钙质结晶，具有典型的陕西黄土特征。在试验土槽取得原状土后，进行室内试验确定土体基本物理性质指标如表1和表2 所示。

表1 试验黄土基本物理性质指标

表2 黄土压缩试验

2.2 模型试验设计

本试验所采用的夯击补强设备为西安长大公路养护技术有限公司研发的HHT-66液压夯实机，设备尺寸为1 359 mm×1 350 mm×3 725 mm，夯锤尺寸为700 mm×700 mm，最大夯击频率为30次/min，最大夯击能量为66 kJ。

如图3所示，试验是在8 m×8 m×1.8 m的模型路基上进行的[17]。路基共分为6层，每层厚0.3 m。路基表面共设12个夯点，每个夯点对应不同的落锤高度和夯击次数。夯锤的落锤高度分别为2.2 m(工况1)、1.6 m(工况2)和0.7 m(工况3)，对应的夯击能分别为66，48和21 kJ。夯击次数分别为3击、6击、9击和12击。夯点尺寸为0.7 m×0.7 m，与夯锤尺寸相同。相邻夯点间距为1 m，既方便液压夯实机连续工作，同时保证夯点之间不发生相互作用[18]。

路基填筑过程中，于各分层界面处铺撒大白粉对标记分层界面进行标记；在夯点及其正下方的各分层界面处埋设沉降钉，通过水准仪测量记录其初始标高；每层各选3处位置用灌砂法测量填土压实度，取均值作为分层压实度。夯击结束后，从路基顶面开始对夯点逐层开挖，用灌砂法进行夯后分层压实度检测，并用水准仪测量沉降钉高程变化以确定夯后各分层界面沉降量。

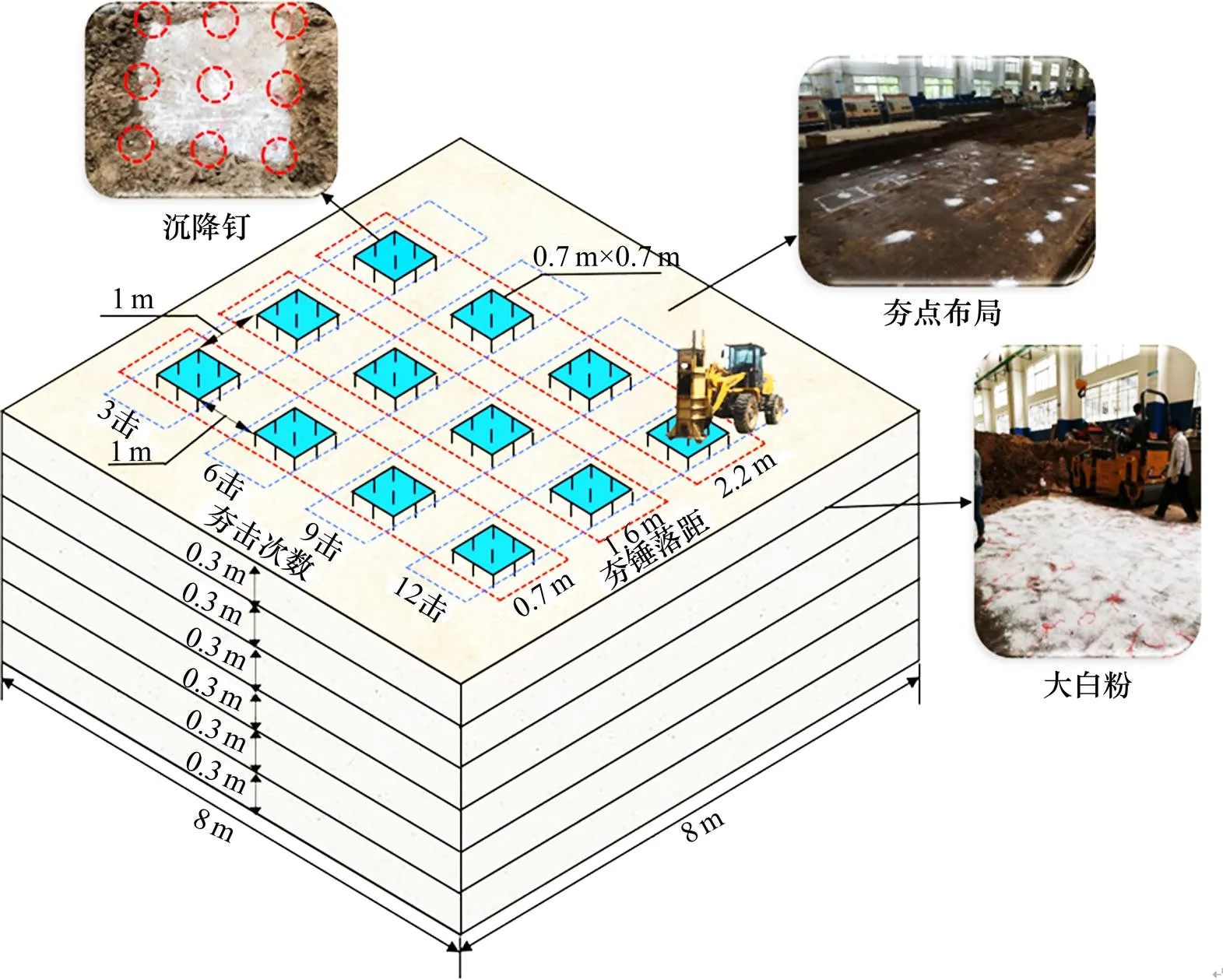
图3 试验分层路基模型

3 数据处理与回归分析

3.1 压实度与沉降量变化规律

表3列出了各夯点处的分层压实度。结果表明，夯锤落距对分层压实度有显著影响。随着深度的增加，压实度的增加值明显减小，当深度达到一定范围(1.5～1.8 m)时，压实效果可以忽略不计。当夯击次数为3时，各层路基的压实度均显著提高，且随着夯击次数的增加，分层压实度增长速率减小。结果表明，夯击次数对路基压实度的改善作用有限，这可能是由于路基初始压实度较大和土体发生回弹所致[19]。

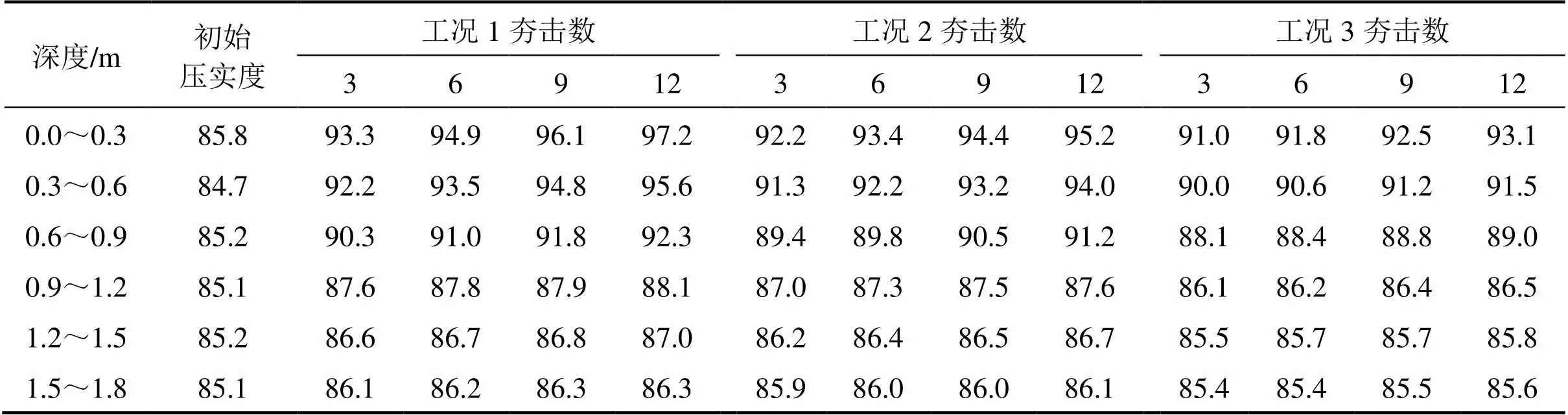
表3 不同夯击次数下分层压实度

图4描绘了各夯点处分层界面沉降量和表层夯沉量的变化曲线。结果表明，分层界面沉降曲线在不同夯锤落距和不同夯击次数下表现出相似的趋势，按深度可分为快速变化区(0～0.9 m)和稳定区(0.9～1.8 m)。快速变化区分层界面沉降量较大，随着深度的增加，沉降迅速减小，且受夯击次数的影响较大。在稳定区，分层界面沉降量较小，随深度增加而缓慢减小，且受夯击次数的影响不明显。随着夯击次数的增加，表面夯沉量增幅下降。当夯击次数达到一定值时(工况1和工况2约为6次，工况3约为9次)，表面夯沉量基本稳定。

(a′)，(a″) 工况1；(b′)，(b″)工况2；(c′)，(c″)工况3

3.2 有效压实深度

由于夯击能量的吸收和消散，随着深度的增加，土体的沉降和压实度增幅均逐渐减小，当深度超过某数值后，夯击的压实效果已经不明显。因此，可以认为只有该深度范围内的土体被有效压实，记为有效压实深度。取压实度值提高≥3%的范围内为有效压实深度，如图5所示。在本试验中，以测得的各层平均压实度为各层中点深度处压实度；由于压实度变化较小，可假设压实度的变化为线性变化[20]，以此确定有效压实深度。

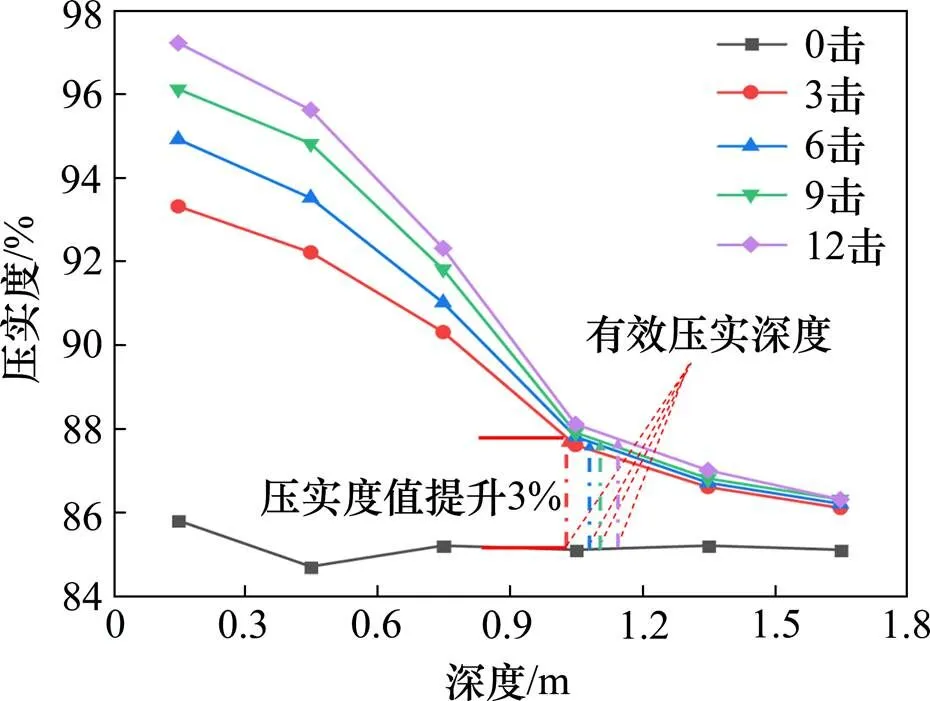
图5 工况1有效压实深度

根据试验所确定的不同工况下的有效压实深度，回归得到有效压实深度与表层夯沉量0之间的关系：

其中：0为初始有效压实深度，与锤重和落距有关；为修正系数。回归计算结果见表4。

表4 有效压实深度回归结果

3.3 分层界面沉降量与深度的关系

模型试验得到的不同工况及不同夯击次数下分层界面沉降量随深度变化的曲线，均具有S型函数的趋势。经回归分析，S型函数中玻尔兹曼函数[21]与分层界面沉降量曲线具有极高的相似度，如式(8)所示：

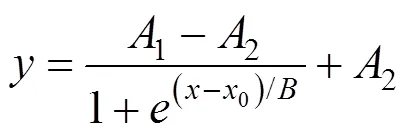
将分层界面沉降曲线按玻尔兹曼函数拟合，如图6为工况1夯击6次情况下的分层界面沉降量与玻尔兹曼函数的拟合情况。

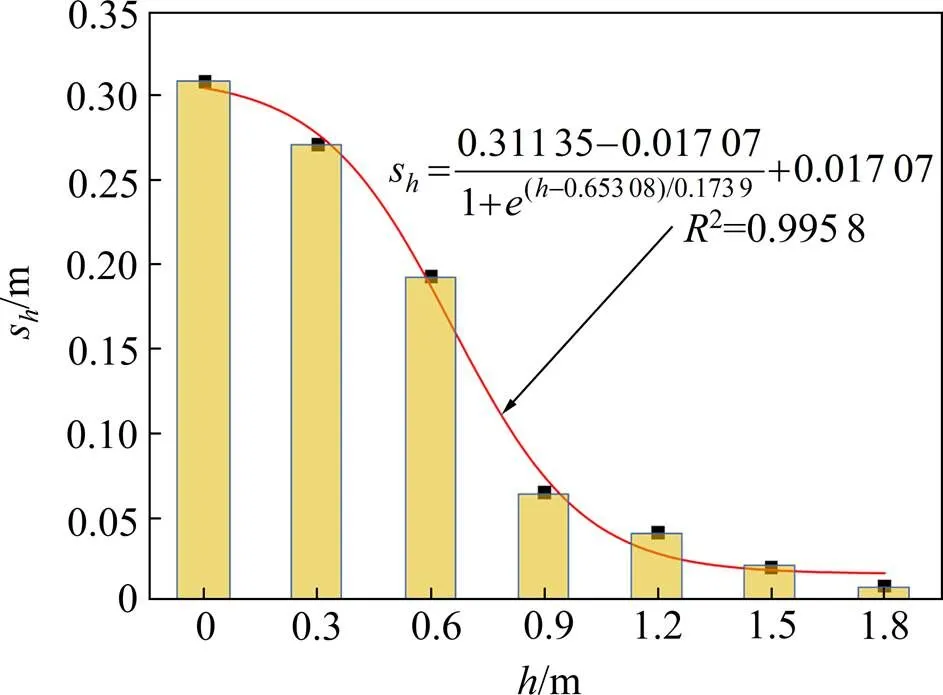
图6 分层界面沉降量拟合曲线(工况1，6击)

分析发现，系数1与表层夯沉量0相似，0接近有效压实深度。推测路基在深度处的沉降量s与有效压实深度及表层夯沉量0相关，从而在玻尔兹曼函数的基础上进行修正，引入曲线拟合系数，和，定义出s与的关系：

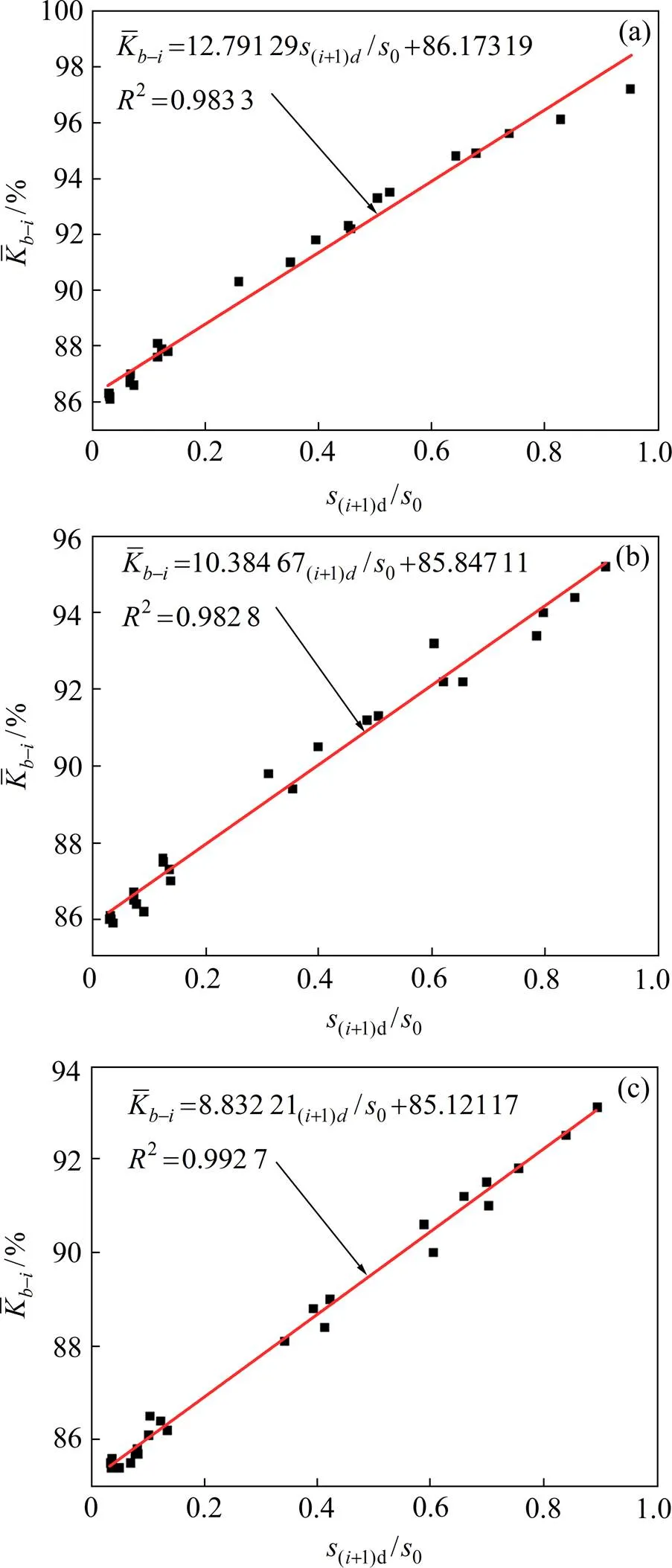
表5为不同工况和不同夯击数下玻尔兹曼函数各拟合参数的取值。通过分别对，和进行线性回归分析，发现表层夯沉量0与修正系数线性相关，有效压实深度与修正系数和线性相关，如图7所示。其拟合得到的计算式如下所示：

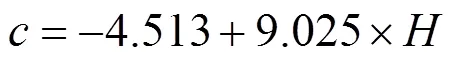
因此，可以利用表层夯沉量与有效压实深度计算修正系数，和。

表5 有效压实深度回归结果

3.4 分层压实度与分层界面沉降量的关系

将夯后各分层压实度值按深度变化绘制曲线，与分层界面沉降量曲线进行对比，发现两者具有较为相似的变化趋势，如图8所示。

进一步地，对各分层压实度值与分层界面沉降量与表层夯沉量之比进行回归分析，其关系符合关系一元线性模型。因此可按下式获取各分层压实度值：

其中：和为拟合系数，根据工况确定取值。

3种不同工况下的拟合情况如图9所示。

3.5 分层土体压缩量修正系数

根据式(6)可得：

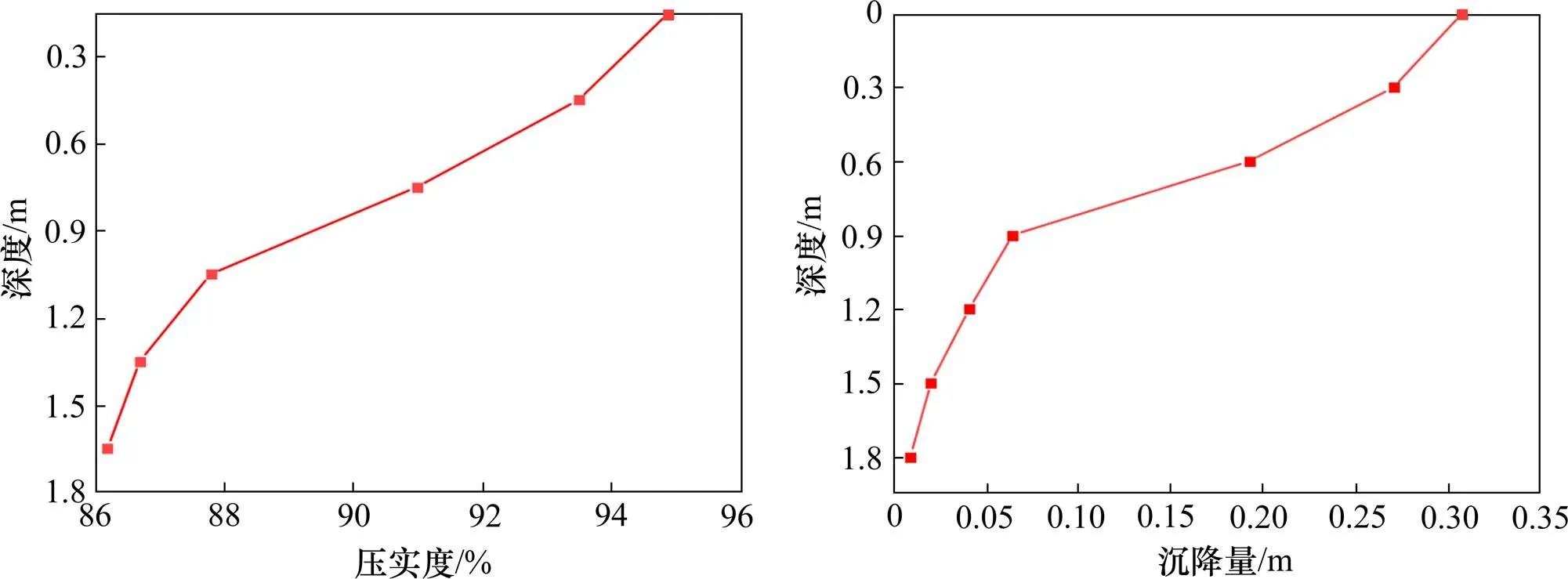
图8 分层压实度曲线和分层界面沉降曲线(工况1，6击)

(a) 工况1；(b)工况2；(c) 工况3

通过对夯前、夯后压实度及夯前深度与夯后深度数据的回归分析，确定各分层的压缩量修正系数如表6所示。

3.6 计算夯前分层压实度

通过计算得到夯后各分层压实度、各分层界面处沉降量后，结合各分层压缩量修正系数，就可以得到夯前路基各分层压实度，如下式所示：

表6 分层修正系数回归结果

至此，实现了计算分层压实度的目标。液压夯实法检测黄土路基压实度的流程可由图10概括表示。

4 应用实例

运用液压夯实法，对某路基工程进行压实度检测。使用压路机对填筑路基进行初次压实，然后选取A、B、C三点，按工况1进行夯击，通过液压夯实机监控设备观察并记录每一击的夯沉量。为保证土体得到充分压实，当单击夯沉量增量小于10 mm时，停止检测，记录数据如表7所示。

图10 液压夯实法检测黄土路基压实度流程图

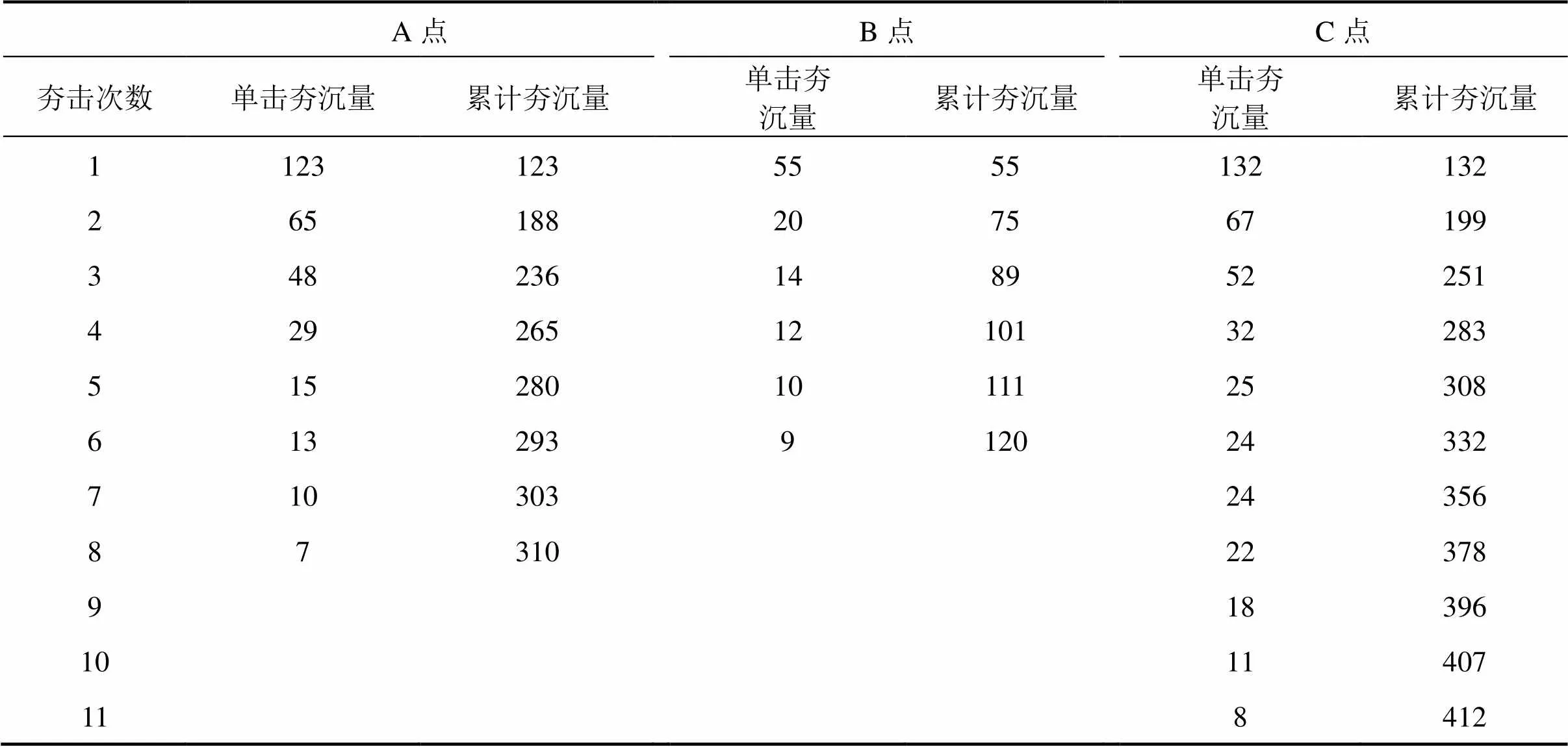
表7 表层夯沉量记录

根据液压夯实法计算，计算过程和结果如表8～11所示。

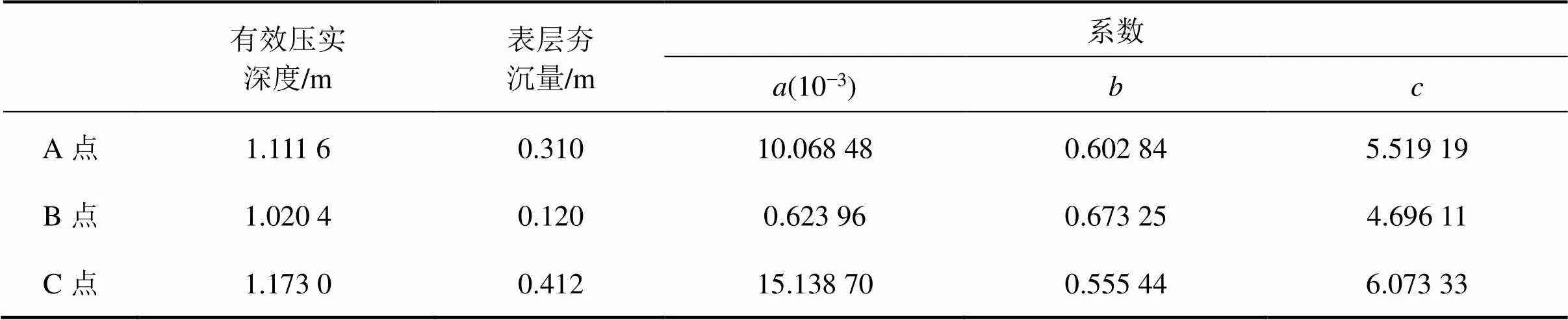
表8 系数计算表

表9 分层界面沉降量计算表

表10 夯后分层压实度计算表

将计算所得结果与灌砂法所得结果对比，如表12所示，其误差均小于2%，说明本文的计算方法是合理可靠的，可以运用此方法检测黄土地区路基压实度，也为黄土地区压实度检测工程提供了经验和指导。

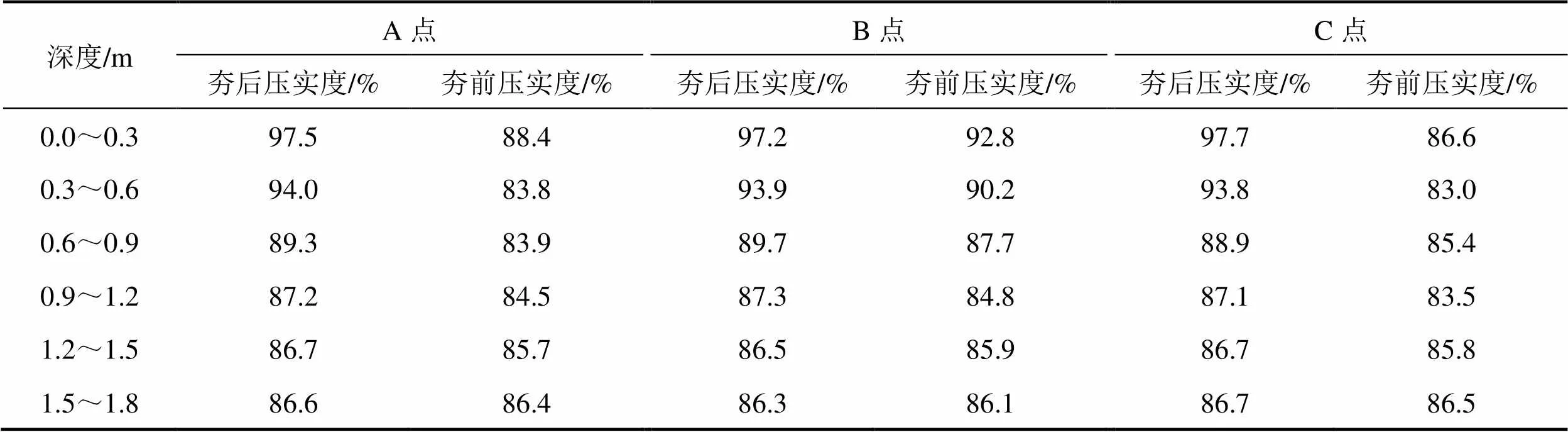
表11 夯前分层压实度计算表

表12 计算数据和实测数据对比

5 结论

1) 根据分层压实理论，推导了液压夯实法检测路基分层压实度的公式，建立了通过分层界面沉降量确定分层压实度的模型。

2) 随着深度增加和夯击次数提高，路基分层界面沉降具有阶段性变化特征，分别以0.8～1.2 m和6～9击为界限。压实度提高值随深度增加迅速衰减，引入有效压实深度的定义，其取值和落锤高度、表层夯沉量相关。

3) 液压夯实法得到的路基分层沉降曲线符合玻尔兹曼函数特征，其参数，和与表层夯沉量和有效压实深度有关；分层压实度值和分层界面沉降量有关，通过回归分析分别得到各参数的函数关系式。

4) 通过实际工程验证，证实该计算方法可靠，为黄土地区路基分层压实度检测提供指导和经验。

研究成果为路基分层压实度检测提供了新的思路，对黄土地区的路基补强检测工程具有指导意义。由于路基土体具有多样性，通过试验数据回归总结得到的计算方法仅适用于陕西地区一般黄土，在检测前建议先对路基土进行试验以获取更为准确的参数值。适用于其他土质的路基分层压实度检测的液压夯实法还有待进一步研究。

[1] ZHOU Zhijun, ZHU Shanshan, KONG Xiang, et al. Optimization analysis of settlement parameters for postgrouting piles in loess area of Shaanxi, China[J]. Advances in Civil Engineering, 2019(12): 1−16.

[2] Smalley I J, Jefferson I F, Dijkstra T A, et al. Some major events in the development of the scientific study of loess[J]. Earth Science Reviews, 2001, 54(1): 5−18.

[3] Regehr J D, Milligan C A, Montufar J, et al. Review of effectiveness and costs of strategies to improve roadbed stability in permafrost regions[J]. Journal of Cold Regions Engineering, 2013, 27(3): 109−131.

[4] LI Zhen, WANG Zhengjun, XIONG Aoyun. The applicability of soil density gauge in the detection of non-cohesive soil[C]// IOP Conference Series: Earth and Environmental Science, 2019(300): 4.

[5] Rabab A, Wassel A B, Amer A, et al. Finite element model to simulate ground improvement technique of rapid impact compaction[J]. Proceedings of the Institution of Civil Engineers-Ground Improvement, 2019(172): 44−52.

[6] Vink J W, Dijkstra J W. CDC Compaction at berth 9 quay extension Felixstowe, UK[J]. Procedia Engineering, 2016(143): 1468−1476.

[7] 工程机械行业“九五”计划及2010年设想[J]. 机电信息, 1996(8): 6−10. “Ninth Five Year Plan”of construction machinery industry and 2010 plan[J]. Electromechanical Information, 1996(8): 6−10.

[8] Erem’Yants V I, Uraimov M. Dynamics of hydraulic vibration machine for soil compaction[J]. Journal of Machinery Manufacture and Reliability, 2009, 38(5): 425−430.

[9] 曹斌. 高速液压夯实机及其军用前景[J]. 工程机械与维修, 2005(4): 86−87. CAO Bin. High speed hydraulic compactor and its military prospect[J]. Construction Machinery and Maintenance, 2005(4): 86−87.

[10] 苏庆波, 李斌. 液压夯实在G205线国道改造工程中的应用研究[J]. 山西建筑, 2013, 39(14): 123−125. SU Qinbo, LI Bin. Study on the application of hydraulic compaction in the reconstruction project of National Highway G205[J]. Shanxi Architecture, 2013, 39(14): 123−125.

[11] 王菲. 高速液压夯实机在公路路基工程中的应用[J]. 交通世界(建养.机械), 2014(5): 74−75. WANG Fei. Application of high-speed hydraulic compactor in highway subgrade engineering[J]. Transportation World (Construction and Maintenance. Machinery), 2014(5): 74−75.

[12] Adam D, Kopf F. Operational devices for compaction optimization and quality control-(Continuous compaction control & light falling weight device)[C]// Proceedings of the Geotechnics in Pavement and Railway Design and Construction, 2004: 97−106.

[13] 司癸卯, 张燕飞, 张成. 快速液压夯实机在地基处理中的应用分析[J]. 中国工程机械学报, 2013(2): 87−90. SI Guimao, ZHANG Yanfei, ZHANG Cheng. Analysis of rapid hydraulic compactor in foundation treatment application[J]. Chinese Journal of Engineering Machinery, 2013(2): 87−90.

[14] 刘本学, 郝飞, 张志峰, 等. 高速液压夯实机动力学模型试验[J]. 长安大学学报(自然科学版), 2009(1): 99−102.

LIU Benxue, HAO Fei, ZHANG Zhifeng, et al. Dynamic model test of high-speed hydraulic compaction[J]. Journal of Chang’an University (Natural Science Edition), 2009(1): 99−102.

[15] 冯雄辉, 万智. 台背液压夯实处理现场试验与数值模拟研究[J]. 铁道科学与工程学报, 2013, 10(1): 49−54. FENG Xionghui, WAN Zhi. Field test and numerical simulation of hydraulic vompaction treatment of abutment back[J]. Journal of Railway Science and Engineering, 2013, 10(1): 49−54.

[16] Ashpiz E S, Zamukhovskiy A V. Subgrade strengthening on the sections for cars interchanging with axle load of 25 t and more[J]. Procedia Engineering, 2017(189): 17−19.

[17] Wersäll C, Nordfelt I, Larsson S. Resonant roller compaction of gravel in full-scale tests[J]. Transportation Geotechnics, 2018(14): 93−97.

[18] WU Y K, SANG X S, NIU B. High-speed hydraulic compactor application in the backfilled of bridge platform[J]. Applied Mechanics and Materials, 2012( 212−213): 1201−1204.

[19] Tarawneh B, Matraji M. Ground improvement using rapid impact compaction: case study in Dubai[J]. Journal of the Croatian Association of Civil Engineers, 2014, 66(11): 1007−1014.

[20] Meehan C L, Tehrani F S, Vahedifard F. A Comparison of density-based and modulus-based in situ test measurements for compaction control[J]. Geotechnical Testing Journal, 2012, 35(3): 387−399.

[21] Ladd A J C. Numerical simulations of particulate suspensions via a discretized Boltzmann equation part II. numerical results[J]. Physics of Fluids, 2015, 271(3): 285−310.

Layered compactness detection method of reinforcement the of loess subgrade

ZHOU Zhijun1, 2, ZHANG Zhipeng1, GUO Tao3, XU Tianyu1

(1. School of Highway, Chang’an University, Xi’an 710064, China;2. Xi’an Highway Engineering Testing Center, Xi’an 710064, China;3. CCECC Fuzhou Survey & Design Institute Co., Ltd., Fuzhou 350013, China)

In order to obtain the layer compactness of subgrade more quickly and effectively, this paper took loess subgrade as an example, and proposed the idea of detecting the subgrade layer compactness achieved by the hydraulic compactor. Based on the theory of layered compaction, the basic model of hydraulic compaction was established and the relationship between the initial layered compactness and the compacted layered compactness was deduced. A full-scale model test of hydraulic compaction was designed and carried out. The results show that the compaction effect can be ignored when the depth is more than about 1.5 m. The layered interface settlement of subgrade and ground settlement have the characteristics of stage change, which are bounded by 0.8～1.2 m and 6～9 tamping times respectively. The concept of improvement depth was introduced and its regression formula was established. The Boltzmann function relationship among ground settlement, improvement depth and layered interface settlement was obtained by regression method. The relationship among compacted layered compactness, layered interface settlement and ground settlement was obtained by linear regression method. The calculationformula of the initial layered compactness of subgrade was deduced and the method for detecting the compactness of loess subgrade was formed. The hydraulic compaction method was applied in a practical project, and the error between the calculation result and the detection result of sand filling method was within 2%.

Road engineering; loess subgrade; hydraulic compaction method; model test; improvement depth