随机风速下桥上汽车行车安全可靠性分析
2021-01-09向圆芳王方立韩艳胡朋蔡春声
向圆芳,王方立,韩艳,胡朋,蔡春声, 3
随机风速下桥上汽车行车安全可靠性分析
向圆芳1,王方立2,韩艳1,胡朋1,蔡春声1, 3
(1.长沙理工大学 土木工程学院,湖南 长沙 410114;2.中国路桥工程有限责任公司,北京 100011;3. 美国路易斯安那州立大学 美国路易斯安那州,巴吞鲁日 LA70803)
为了探讨风速的随机性对桥上行车安全可靠性的影响,首先通过CFD数值模拟获得了桥上车辆的气动力系数;基于提出的移动点脉动风速谱,随机生成移动车辆的脉动风速;基于风-车-桥系统耦合振动分析,考虑风速的随机性,建立了一种求解系统失效概率的极限状态函数模型,采用响应面方法对桥上汽车行车安全进行了可靠性评估。计算结果表明:桥上车辆横风失效概率随风速和车速的增大而增大;车速越高,车辆安全行驶对风速的敏感程度越高;基于可靠性理论模拟的概率特征风速曲线能够较合理地评估随机风速下桥上车辆的行车安全性。
风−车−桥系统;CFD数值模拟;随机风速;行车安全;可靠性分析
汽车行驶在强风环境下,所受侧力和升力(侧力和升力是引起行车安全事故的主要原因)急剧增大,容易引发行车安全事故。据不完全统计,我国每年由大风引发的交通事故超过1 600起,直接经济损失达数千万元[1]。当前,横风已成为影响汽车行车安全的重要因素之一。针对桥上汽车行车安全,国内外学者开展了大量研究。Baker[2]最早对风荷载作用下地面汽车行车安全进行了系统研究,并给出了汽车发生侧翻、侧滑等事故的判别准则。CHEN 等[3]通过建立风−汽车−桥梁耦合振动模型,改进了车辆事故风险评估方法。GUO等[4]提出了一种侧风作用下大跨度斜拉桥上汽车行车安全的分析方法。韩万水等[5]建立了风−汽车−桥梁系统耦合振动分析模型,分析了路面粗糙度水平、风速以及干湿雨雪等路面条件对车辆安全行驶的影响,得到了典型车辆在桥梁上安全行驶的临界风速。马麟[6]将驾驶员反应行为模型引入风−汽车−桥梁系统整体运动方程, 得到了不同风速下桥梁上发生行车安全事故的临界车速。韩艳等[7−10]通过数值模拟和风洞试验方法分析了风−汽车−桥梁耦合系统车桥间的相互气动干扰分别对车辆和桥梁气动力的影响,研究表明,考虑车辆和桥梁间相互的气动干扰对于分析桥梁上车辆安全事故发生的类型和临界风速具有重要的意义。以上针对横风作用下汽车行车安全研究主要采用确定性分析方法,并未考虑系统参数以及输入的不确定性。事实上,由于湍流的存在,自然风具有一定的随机性,由此引发的车辆或车辆−桥梁系统振动也是一个随机过程[11]。Snabjörnsson 等[10−11]较早采用概率模型对随机风环境下汽车行车安全事故进行了可靠性评估。然而,这些研究主要是关注地面车辆,并未考虑桥面上行车安全性问题。Kim等[12]利用桥址处的长期风数据以及桥面板和车辆的空气动力特性,提出了一种评估横风作用下桥上车辆行驶风险的方法。庞加斌等[13]通过建立桥面行车高度处的等效风速概率模型,提出了侧风下桥上行车安全概率评估方法。这2种方法均以桥上行车为研究对象,却忽略了桥梁振动对车辆的影响。基于风−汽车−桥梁耦合振动模型,李永乐[14]建立了包含概率统计因子的车辆行车安全评价指标。然而,该研究并未考虑输入的随机性。本文基于风−汽车−桥梁耦合振动并考虑随机风速,建立一种求解失效概率的极限状态函数模型,采用响应面法对桥上汽车行车安全进行可靠性评估。数值算例中,以东平河特大桥为研究对象,分别给出了不同车速和风速下的车辆失效概率,评估了车辆行车安全可靠性。
1 桥上车辆行驶安全性分析方法
风−汽车−桥梁耦合分析中,车辆模型采用拉格朗日原理建立,桥梁模型采用有限元结合模态叠加法建立,车桥间相互作用采用虚功原理建立,风荷载作为外荷载直接施加在桥梁和车辆上。参考文献[15]给出了具体的车辆和桥梁模型及车桥间相互作用关系的推导,则风−汽车−桥梁耦合系统的运动方程为:


以上各式具体含义详见参考文献[16]。
行车安全性分析参考HU等[17]提出的车辆事故分析模型,假定车轮与桥面“密贴”,车体质心相对地面存在侧滑位移,根据力的平衡方程及力和位移的协调条件得到车辆事故分析状态矢量空间方程为:
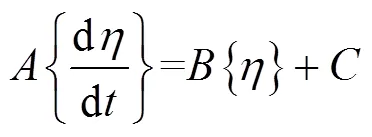
式中:,和的表达式及,的具体含义详见参考文献[15]。
2 车辆气动力荷载计算
2.1 桥上车辆气动力系数的数值模拟
本文以东平河特大桥为研究背景,其主梁断面尺寸如图1(a)所示,车辆三维模型如图1(b)所示。数值模拟时将车辆放置于桥面第一车道,车辆距离桥面中心7.5 m,距离桥梁风嘴前端点10.75 m,桥梁纵向延伸80 m,车辆中心位于桥梁纵向中心位置。
单位:m
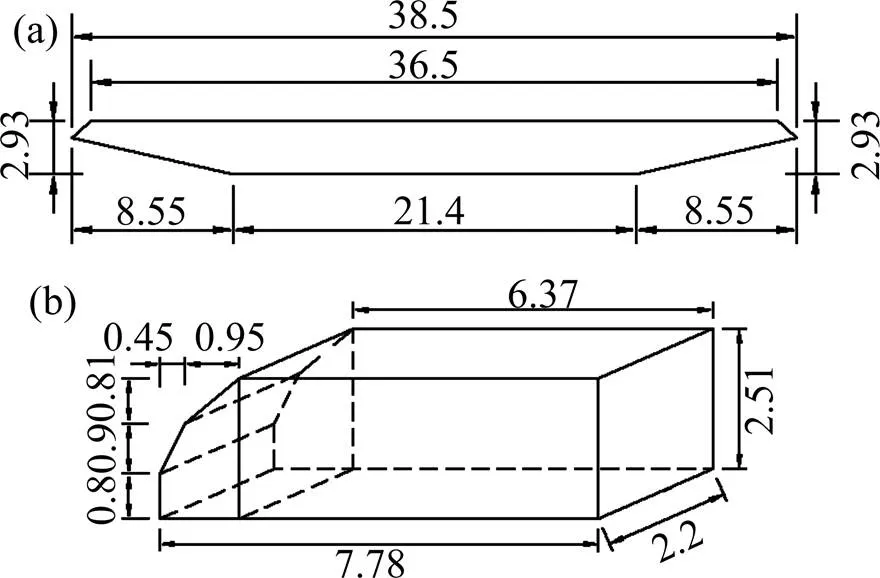
本文采用CFD进行计算分析,在ICEM 中实现网格划分。湍流模型选用SST模型。特征长度取主梁断面的高度,计算域上游入口距主梁断面20,下游出口距主梁断面54,上下边界高度取为20。在ICEM中建立的计算域及车桥模型如图2所示。为满足计算精度要求,整个流场采用全六面体网格,第1层网格高度取0.001 m,车辆的+值为1.8左右,满足计算要求。对总网格数为100万,300万和500万3种网格进行网格无关性测试后,最终确定模型网格数量为300万,车桥网格如图3所示。
图2 计算域及车桥相对位置

图3 网格划分示意图
边界条件的确定:流场入口采用速度边界(Velocity inlet)条件,有风偏角时,采用笛卡尔分量表示合成速度,无风偏角时,切向速度取0,只有法向速度;流场出口采用压力边界(Pressure outlet)条件,相对压力取0;有风偏角时,前壁面采用速度边界(Velocity inlet)条件,后壁面采用压力边界(Pressure outlet)条件,相对压力取0,无风偏角时,前后壁面均采用自由滑移(Free slip)边界;上下壁面采用Symmetry边界。
计算桥上车辆的气动力系数时,参考面积为车辆行驶方向迎风面投影面积,参考高度为车体质心到桥面的垂直距离h,则桥上车辆气动力系数的定义为:





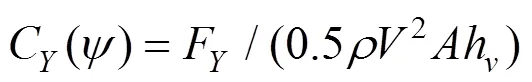
式中:为空气密度,F,F,F,F,F和F分别表示作用在车体质心点的升力、侧力、阻力、侧倾力矩、俯仰力矩和偏转力矩,车辆气动力方向如图4所示;C,C,C,C,C和C分别表示车辆的升力系数、侧力系数、阻力系数、侧倾力矩系数、俯仰力矩系数和偏转力矩系数;表示相对车辆的风速,其偏角为;车速与来流风速的关系如图5所示,其中表示车速;表示自然风速;表示自然风的风向角。


图5 车速与来流风速关系图
图6给出了车辆气动力系数随风偏角的变化关系。由图6可以看出,侧力系数在风偏角为0°最小,随着风偏角的增大而增大。阻力系数随着风偏角先增大后减小再增大,风偏角为15°时阻力系数达到最大值。阻力系数在风偏角为90°时接近0,也就是说当风速方向与车辆前进方向垂直时,车辆基本不受阻力作用,与实际情况符合。随着风偏角的增大,升力系数先增大再减小,并且在风偏角为15°~60°范围内为正值,说明该风偏角范围不利于行车安全。俯仰力矩系数和偏转力矩系数的数值较小,并且呈现出离散性。侧倾力矩系数整体有随着风偏角的增大而逐渐减小的趋势。由于车辆气动力系数是风偏角的函数,与车速和风速无关,根据三角函数拟合得到车辆气动力系数与风偏角的关系式为:



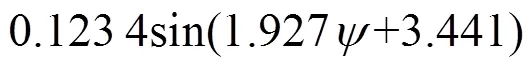
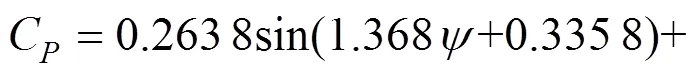
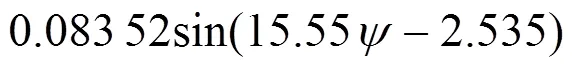


以上各个公式相关系数分别为0.996 5,0.977 7,0.987 7,0.999 7,0.982 2和0.939 8,残差和分别为0.01,0.000 5,0.001 4,0,0.026,0.000 3,拟合效果较好。
2.2 移动车辆的脉动风速模拟
车辆行驶过程中所受的脉动风速仅考虑纵向脉动分量,采用Carrarini[18]提出的横风下移动点脉动风速谱S进行模拟,S具体表达式见式(10)。地表粗糙高度取0=0.05 m,截止频率ω=4 π rad/s;频率等分点数取1 024,衰减系数取7。采用谐波合成法模拟的车速10 m/s,平均风速20 m/s时脉动风速时程曲线如图7所示。
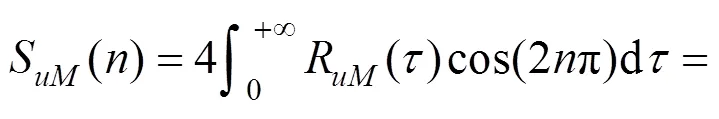

式中:为频率为自相关函数;S为自相关函数; 为纵向脉动风速均方差。,和的表达式详见参考文献[15]。
3 随机风速下行车安全可靠性分析
3.1 行车安全可靠性分析模型
在实际车辆行驶过程中,风−汽车−桥梁耦合系统参数具有不确定性。因此不能确定车辆在给定条件下是否一定行驶安全,只能确定其发生安全事故的概率,即失效概率。


式中:p为失效概率。
式(11)可以调整为:

式(8)给出了车速和失效概率的确定时,车辆安全行驶所能承受的最大平均风速,可以将式(8)看作传统特征风速曲线的推广,称其为概率特征风速曲线(PCWC)[19],即有:


(a) 侧力系数;(b) 阻力系数;(c) 升力系数;(d) 侧倾力矩系数;(e) 偏转力矩系数;(f) 俯仰力矩系数
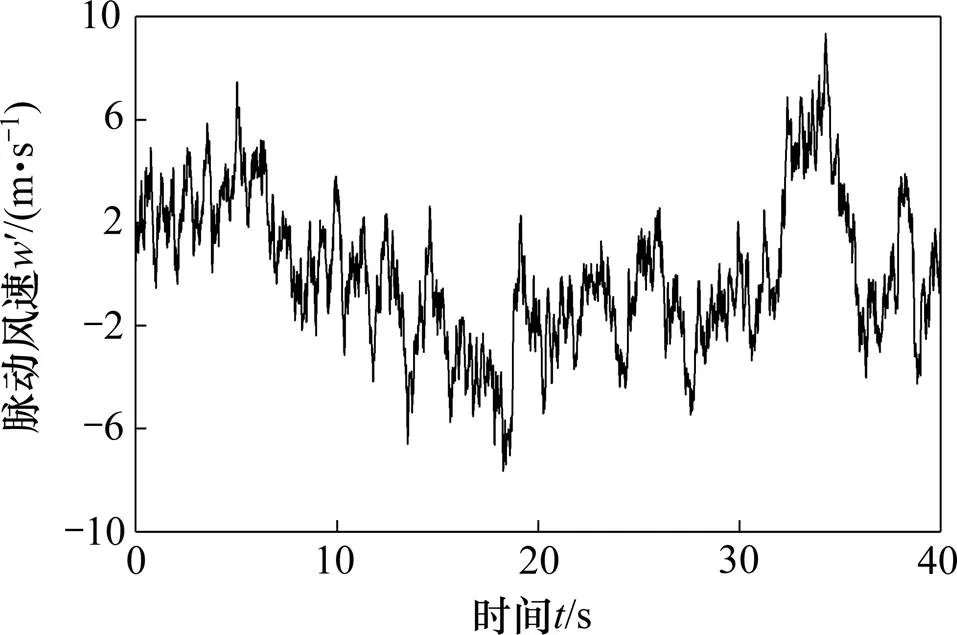
图7 脉动风速时程曲线
3.2 基于响应面法的失效概率的计算
在结构可靠性分析中,用极限状态函数=() (也称为功能函数)来描述系统的状态,失效概率p可以表示为:

在行车安全性分析时,文中以侧滑事故和侧翻事故为评判准则[2]:当滑移超过0.5 m时,则认为发生侧滑事故;当某一车轮的接触力为0时,则认为发生侧翻事故。由于求解车辆的侧滑位移和车轮的接触力的过程非常复杂,在进行可靠度分析时,不能明确给出侧滑极限状态函数或者侧翻极限状态函数的表达式,因此本文采用响应面法求解。其基本思想是用一个相对简单的显式函数来代替复杂的隐式极限状态方程,通过迭代来实现响应面函数的失效概率高度近似于隐式极限状态函数的失效概率。本文选用不含交叉项的二次多项式函数作为响应面函数,响应面函数表达式如下:

式中:为随机变量的个数,,,为系数,求解此方程最少需要2+1个随机试验点。
在行车安全分析中,一旦发生侧滑事故或者侧翻事故,则认为系统失效。研究表明[20],不同车速下系统失效时发生的事故类型不完全相同。因此,在进行行车安全可靠性评估时,有必要综合考虑侧滑和侧翻2种事故类型。本文采用直接Monte Carlo方法求解失效概率时建立一种功能函数的表达方法,即将侧滑功能函数和侧翻功能函数用或的逻辑运算符连接起来,当任意一个功能函数小于等于0时,则输出系统失效。具体计算流程如图8所示。

图8 计算流程图
4 算例分析
4.1 工程背景及计算参数
东平河特大桥主桥总体布置为65+75+268 m,总长408 m,如图9所示。主桥为独塔双跨双索面混合梁斜拉桥。主梁采用全封闭箱型断面和钢-混凝土混合梁设计方案,主梁全宽38.5 m,顶面宽36.5 m。东平河特大桥的气动参数取自文献[20],采用0°攻角下的桥梁气动力系数,阻力系数为0.928 95;升力系数为−0.243 59;扭矩系数为−0.123 72。采用有限元分析软件ANSYS建立桥梁结构的三维有限元模型,结构阻尼比取0.005,计算得到的桥梁结构前10阶动力特性见表1。
文中车辆计算模型采用7个自由度的两轴厢式货车,车体考虑竖向沉浮、绕轴的俯仰、绕轴的侧倾3个自由度,4个车轮分别考虑竖向位移自由度。车辆的动力学参数采用文献[15]中的参数。首先采用模态叠加法进行风−汽车−桥梁耦合振动分析,然后将计算得到的车辆竖向、绕轴的侧倾及绕轴的俯仰动力响应用于车辆事故分析模型,运用四阶龙格库塔算法计算得到车辆的侧滑位移和车轮反力。

单位:cm

表1 东平河特大桥的前10阶动力特性
4.2 响应面法计算失效概率


表2 各试验点的侧滑位移响应
通过表2采用最小二乘法拟合确定车速10m/s时发生侧滑事故的响应面函数为:
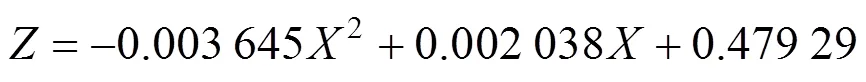
同理可得车速分别20,30和40 m/s时发生侧滑事故的响应面函数分为:
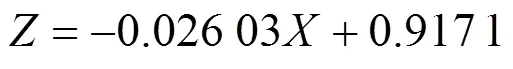

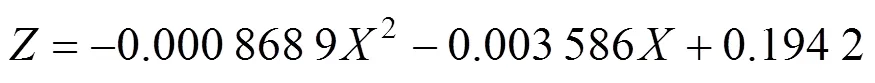
采用直接Monte Carlo方法可计算得到车速分别为10,20,30和40 m/s时对应的不同风速下的侧滑失效概率,同理可得车速分别为10,20,30和40 m/s时对应的不同风速下的侧翻失效概率。
图10给出了不同车速和不同风速下车辆发生侧滑事故和侧翻事故的失效概率。由图10可知,当车速一定时,随着风速的增加,车辆发生侧滑事故和侧翻事故的失效概率均增大;当风速一定时,车速越大,车辆发生侧滑事故和侧翻事故的失效概率均越大。因此,在风速较大的环境中,必须降低行车速度来减小车辆发生侧滑事故和侧翻事故的概率。
基于提出的行车安全可靠性分析方法,综合考虑侧滑事故和侧翻事故,图11给出了随机风环境下行车安全可靠性分析结果。为了与传统的确定性方法的结果进行比较,特征风速曲线(CWC)也在图中给出。由图11可知,当车速为10 m/s时,传统的确定性方法计算得到临界风速为35 m/s,也就说,当风速低于35 m/s时,判定不会发生行车事故;当风速高于35 m/s时,判定会发生行车事故。而基于可靠性分析结果表明,当平均风速低于临界风速时,仍有发生安全事故的可能;当平均风速高于临界风速时,系统也不是一定失效,即不一定会发生行车事故,而是失效概率随着风速增加而增大并逐渐接近于1。由此说明,基于可靠性的分析结果比传统的确定性结果更加符合真实情况。当车速为10 m/s,失效概率由0.001增加到0.99时,车辆安全行驶可承受的最大风速约增加29 m/s;当车速为40 m/s,失效概率由0.001增加到0.99时,车辆安全行驶可承受的最大风速约增加3 m/s。说明车速越高,车辆安全行驶对风速的敏感程度越高,从而车辆在高速行驶时,需要特别注意风速的变化。图11给出了给定失效概率下,车辆安全行驶所允许的最大车速和平均风速的组合。在环境风速确定的情况下,桥梁相关管理部门可以选定一个车辆安全行驶所能接受的最大失效概率,对桥上来往车辆进行合理的限速。
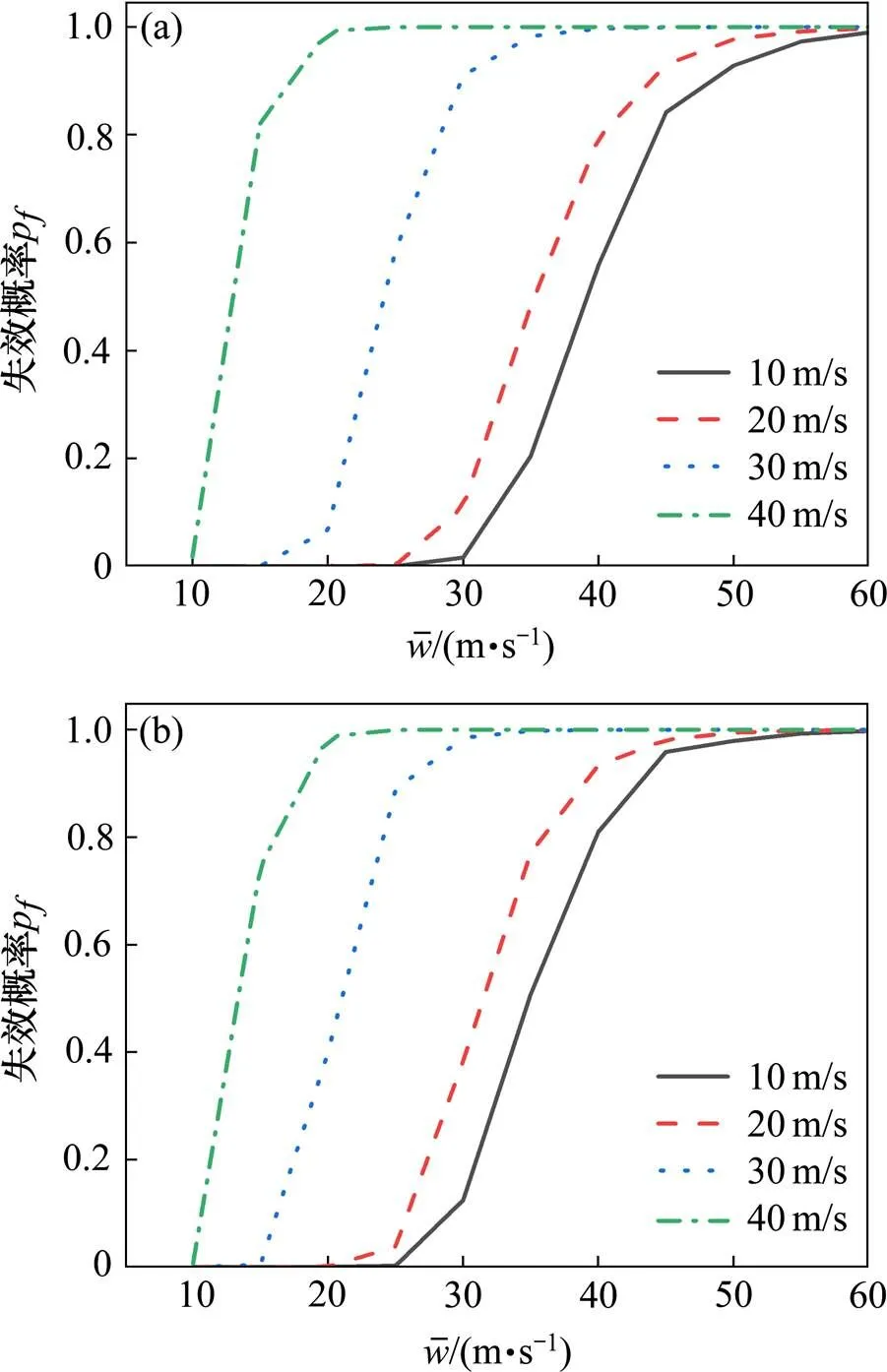
(a) 侧滑失效概率;(b) 侧翻失效概率
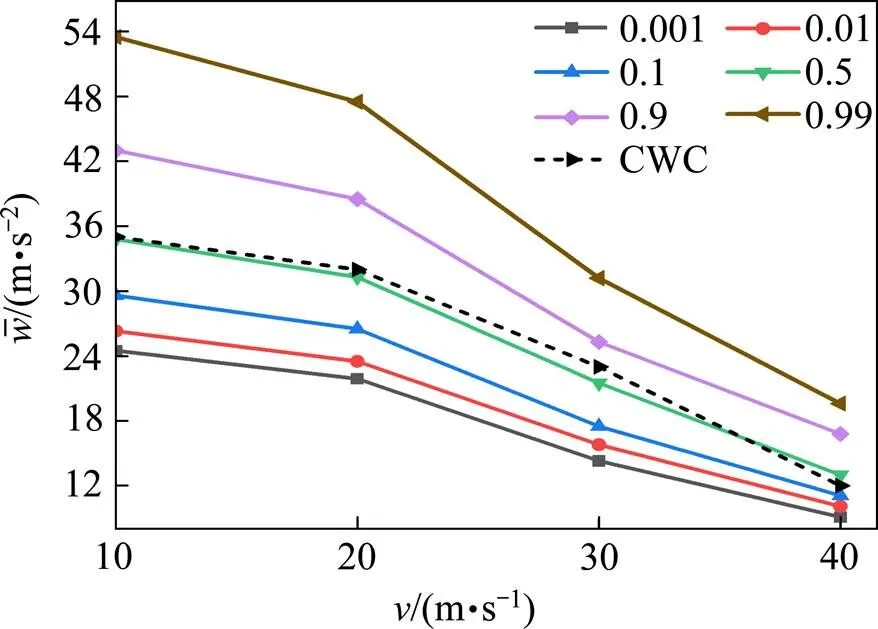
图11 概率特征风速曲线
5 结论
1) 将风速考虑为随机变量,通过功能函数表征桥上车辆行车安全性,利用响应面法计算其失效概率,并以此评价桥上车辆在随机风荷载作用下的安全性,更加符合实际情况。
2) 桥上车辆横风失效概率随风速和车速的增大而增大,车速越高,车辆安全行驶对风速的敏感程度越高。
3) 模拟出车辆的特征风速曲线和概率特征风速曲线,可有效评估车辆在某一固定车速和风速下发生事故的概率。风速一定时,相关部门可选定一个可以接受的最大失效概率,从而对来往车辆进行合理的限速,为桥梁的安全管理提供依据。
[1] 宁贵财, 康彩燕, 陈东辉, 等. 2005~2014年我国不利天气条件下交通事故特征分析[J]. 干旱气象, 2016, 34(5): 753−762. NING Guicai, KANG Caiyan, CHEN Donghui, et al. Analysis of characteristics of traffic accidents under adverse weather conditions in china during 2005~2014[J]. Journal of Arid Meteorology, 2016, 34(5): 753− 762.
[2] Baker C J. A simplified analysis of various types of wind-induced road vehicle accidents[J]. Journal of Wind Engineering Industrial Aerodynamics, 1986, 22(1): 69− 85.
[3] CHEN S R, CAI C S. Accident assessment of vehicles on long-span bridges in windy environments[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2004, 92(12): 991−1024.
[4] GUO W, XU Y. Safety analysis of moving road vehicles on a long bridge under crosswind[J]. Journal of Engineering Mechanics, 2006, 132(4): 438−446.
[5] 韩万水, 陈艾荣. 风−汽车−桥梁系统空间耦合振动研究[J]. 土木工程学报, 2007, 40(9): 53−58. HAN Wanshui, CHEN Airong. Three-dimensional coupling vibration of wind-vehicle-bridge systems[J]. China Civil Engineering Journal, 2007, 40(9): 53−58.
[6] 马麟. 考虑驾驶员行为的风−汽车−桥梁系统空间耦合振动研究[D]. 西安:长安大学, 2008. MA Lin. Three-dimensional coupled vibration of wind- vehicle-bridge system considering driver’s behavior[D]. Xi’an: Chang’an University, 2018.
[7] 韩艳, 胡揭玄, 蔡春声, 等. 横风下车桥系统气动特性的风洞试验研究[J]. 振动工程学报, 2014, 27(1): 67−74. HAN Yan, HU Jiexuan, CAI Chunsheng, et al. Wind tunnel measurement on aerodynamic characteristics of vehicles and bridges under cross winds[J]. Journal of Vibration Engineering, 2014, 27(1): 67−74.
[8] 韩艳, 胡揭玄, 蔡春声, 等. 横风作用下考虑车辆运动的车桥系统气动特性的数值模拟研究[J]. 工程力学, 2013, 30(2): 318−325. HAN Yan, HU Jiexuan, CAI Chunsheng, et al. Numerical simulation on aerodynamic characteristics of vehicles and bridges under cross winds with the consideration of vehicle moving[J]. Engineering Mechanics, 2013, 30(2): 318−325.
[9] 韩艳, 刘叶, 黄静文, 等. 考虑车桥间气动干扰的桥上车辆行驶安全性分析[J]. 湖南大学学报(自然科学版), 2019, 46(7): 76−85. HAN Yan, LIU Ye, HUANG Jingwen, et al. Traffic safety analysis of vehicles on a bridge considering the aerodynamic interference between vehicles and bridge[J]. Journal of Hunan University (Natural Science), 2019, 46(7): 76−85.
[10] Snabjörnsson J T, Baker C J, Sigbjörnsson R. Probabilistic assessment of road vehicle safety in windy environments[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2007, 95(9−11): 1445−1462.
[11] Proppe C, Wetzel C. A probabilistic approach for assessing the crosswind stability of ground vehicles[J]. Vehicle System Dynamics, 2010, 48(Suppl 1): 411−428.
[12] Kim S J, Yoo C H, Kim H K. Vulnerability assessment for the hazards of crosswinds when vehicles cross a bridge deck[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2016, 156: 62−71.
[13] 庞加斌, 王达磊, 陈艾荣, 等. 桥面侧风对行车安全性影响的概率评价方法[J]. 中国公路学报, 2006, 19(4): 63−68. PANG Jiabin, WANG Dalei, CHEN Airong, et al. Probability evaluating method of bridge deck side wind effects on driving safety[J]. China Journal of Highway and Transport, 2006(4): 63−68.
[14] 李永乐, 赵凯, 陈宁, 等. 风−汽车−桥梁系统耦合振动及行车安全性分析[J]. 工程力学, 2012, 29(5): 206−212. LI Yongle, ZHAO Kai, CHEN Ning, et al. Wind- vehicle-bridge system coupling vibration and traffic safety analysis[J]. Engineering Mechanics, 2012, 29(5): 206−212.
[15] HAN Yan, CAI C S, ZHANG J, et al. Effects of aerodynamic parameters on the dynamic responses of road vehicles and bridges under cross winds[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2014, 134: 78−95.
[16] CHEN S R, CAI C S. Accident assessment of vehicles on long-span bridges in windy environments[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2004, 92(12): 991−1024.
[17] HU Peng, HAN Yan, CAI C S, et al. New analytical models for power spectral density and coherence function of wind turbulence relative to a moving vehicle under crosswinds[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2019, 188: 384−396.
[18] Carrarini A. Reliability based analysis of the crosswind stability of railway vehicles[D]. Berlin: Technischen University Berlin, 2006.
[19] HAN Yan, HUANG Jingwen, CAI C S, et al. Driving safety analysis of various types of vehicles on long-span bridges in crosswinds considering aerodynamic interference[J]. Wind and Structures, 2019, 29(4): 279− 297.
[20] 韩艳, 李春光, 董国朝, 等. 东平河特大桥抗风性能研究报告[R]. 长沙: 长沙理工大学风工程试验研究中心, 2017.HAN Yan,LI Chunguang, DONG Guochao, et al. Research report on wind resistance performance of Dongping river great bridge[R]. Changsha: Changsha University of Science and Technology Wind Engineering Experimental Research Center, 2017.
Analysis of vehicle safety and reliability on the bridge exposed to stochastic winds
XIANG Yuanfang1, WANG Fangli2, HAN Yan1, HU Peng1, CAI Chunsheng1, 3
(1. School of Civil Engineering, Changsha University of Science & Technology, Changsha 410114, China; 2. China Road & Bridge Corporation, Beijing 100011, China; 3. Louisiana State University, Baton, LA70803, Louisiana, USA)
This study investigated the effect of the randomness of wind speed on the reliability of the driving safety of vehicles on the bridge. Firstly, the aerodynamic coefficients of vehicles on the bridge were obtained by CFD numerical simulation. The fluctuating wind speed of a moving vehicle was generated randomly based on the proposed fluctuating wind speed spectrum of a moving vehicle. Based on the coupled vibration analysis of the wind-vehicle-bridge system, considering the randomness of wind speed, a limit state function model was established to solve the failure probability, and the response surface method was used to evaluate the reliability of vehicle driving safety on the bridge. The results show that the probability of failure increases with the increase of wind or vehicle speed under crosswinds. Vehicle safety is more sensitive to wind speed as vehicle speed increases. The characteristic wind speed curve based on the reliability theory can reasonably evaluate the vehicle safety under random wind speed.
wind-vehicle-bridge system; CFD numerical simulation; stochastic winds; driving safety; reliability analysis

U447
A

1672 − 7029(2020)12 −3126 − 09
10.19713/j.cnki.43−1423/u.T20200137
2020−02−25
国家自然科学基金优秀青年基金资助项目(51822803);湖南省杰出青年基金资助项目(2018JJ1027);湖南省教育厅优秀青年基金资助项目(16B011)
韩艳(1979−),女,江苏连云港人,教授,博士,从事大跨度桥梁风致振动与振动控制研究、风−车−桥耦合振动与行车安全性研究;E−mail:ce_hanyan@163.com
(编辑 阳丽霞)
