傅科摆的几何分析1)

王睿垠 袁 威 冯 放 金长江

*(东北农业大学文理学院，哈尔滨150030)

†(东北农业大学工程学院，哈尔滨150030)

1851年，傅科 (Jean Foucault，1819–1868年)在200英尺长的绳索上搭建了一个由重铁球构成的单摆来证实地球的自转[1]。傅科观察到，地球的自转会导致单摆的摆动面转动[2]。摆动面转动角度会随纬度变化，每天摆动面(垂直向下看北半球为顺时针)转动角度为 2πsinθ(θ表示摆所处的纬度)，如北极每天转动角度为 2π、赤道处转动角度为 0(如图1所示)。从傅科公开展示他的实验之后，傅科摆在物理学、物理学教育以及科学史中发挥了重要作用[3]，其基本原理还应用到电动力学、核物理学、量子力学、固体力学等其他物理方向[4]。

目前国内很多科技馆都有傅科摆装置，但即使是学过大学物理课程的学生，仍不能很好地理解傅科摆的工作原理。摆平面的转动现象，可以通过大学物理中的旋转参考系和科里奥利力来解释，由于概念较为抽象，因此对非物理专业的学生来说理解摆的行为与地球自转的关系仍然是个难点。傅科摆提供了一个在几何学背景下进行数学建模的典型实例[5]，一些傅科摆的研究由于直接应用黎曼几何方法[6-7]，因此在方法上显得与牛顿力学毫无关联。本文把傅科摆的行为与几何联系在一起，给出了研究傅科摆的几何方法，并且通过与牛顿力学方法比较证明了两种方法的等价性。本文旨在让学生了解几何方法在力学实践的重要性[8]，以期通过傅科摆的几何描述引起读者应用微分几何解决力学问题的兴趣。

图1 地球上不同纬度的傅科摆

1 傅科摆的牛顿力学分析

分析傅科摆的牛顿力学方法，可以参考一些文章和教材[9-13]。给定固定于地球上的体坐标系x，y，z(即观察者自身坐标系)，如图2所示。假设摆的长度L很长，忽略摆球在z方向的位移以及地球转动产生的离心力，可以得到摆球的运动方程

式中，m为摆球的质量，r为摆球的矢径，g为重力加速度，Ω为地球角速度矢量。

图2 傅科摆的坐标系

由于x，y远小于L，T～=mg，可以得到绳索张力T在坐标轴的投影为

式(1)科氏加速度项中

计算时忽略了z方向的位移，即˙z=0。把式(1)向x，y方向投影，根据式(2)和式(3)，可以得到傅科摆的运动方程为

式中，ω2=g/L，ΩZ=Ωsinθ。

取μ=x+iy，式(4)写成微分方程为

考虑到Ωz远小于ω，方程的解为

式中，括号内是没有地球自转影响时摆的运动，而e－iΩzt表示了摆平面如何转动。取μ0=x0+iy0=Aeiωt+Be－iωt，则摆平面的转动方程为

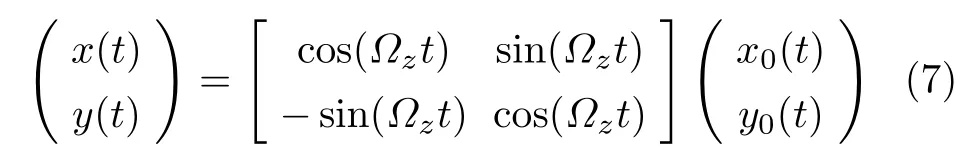
x0(t)，y0(t)为初始条件。地球转动一天的时间为t0=2π/Ω。当地球转动一圈时，由式(7)可以算出摆平面转过的角度为Ωzt0=Ωsinθ(2π/Ω)=2πsinθ。

2 傅科摆的空间解释

与大学物理中用科里奥利力解释傅科摆不同，这里从另一个角度来研究傅科摆。相对于静止坐标系，摆平面在平直空间移动时不会发生任何偏转。假设地球是不转的，傅科摆在球体上沿纬度不变的方向移动一周，对于摆来说，摆平面转动的角度和地球自转的效果是相同的[14]。直观上很容易解释矢量(即摆球速度矢量)沿固定纬度方向的转动[15]。把沿固定纬度的路径外接一个圆锥，圆锥可以拓扑同胚于二维平面，这样圆锥展开面上的直线即为曲面上的直线，球面上矢量的平移如图3所示。

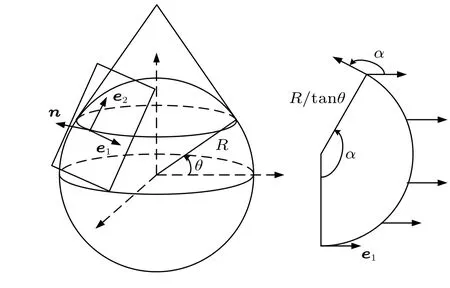
图3 固定纬度的路径

从图3可以看到，地球是圆锥内接球，矢量绕固定纬度走一圈，方向的改变量为α，将圆锥展后可以直接计算结果。圆锥的母线长为R/tanθ，同纬度圆的周长为 2πRcosθ，故矢量转过的角度为α=2πRcosθ/(R/tanθ)=2πsinθ。如果傅科摆处于地球纬度为θ的位置，那么摆平面一天转过的角度为2πsinθ，该结果与牛顿力学的矢量分析结果相同。

3 傅科摆的几何分析

研究傅科摆在任意轨道上的转动时，上述解释不能适用，因此考虑采用微分几何的分析方法来研究傅科摆。

先考虑摆平面在曲面上的偏转问题。二维生物在球面上看球体与鸟在空中看球体是不同的。二维生物仅能感知经度和纬度的二维空间，对于三维空间中的任何事件或物体，二维生物只能通过投影到切平面上来感知。三维向量在地球的切平面上可以写为v=ae1+be2+cn，如图3所示，二维生物只能感知到切平面上的ae1+be2。任何空间中，直线的特征是物体沿该直线匀速运动时，加速度矢量为零。通过类比，二维球面上的直线(测地线)可以定义为：当物体匀速运动并且切于球面的加速度为零时，物体经过的路径为直线。二维生物感知到匀速运动物体在ae1+be2方向的加速度为零(但沿n方向加速度可以不为零)的任何曲线都是直线，可以证明该直线就是球面上的大圆。如果傅科摆的摆球速度矢量平移方向是测地线方向，摆平面是不会转动的，否则会有沿切平面方向的加速度，摆平面一定转动。

再看矢量随坐标线平移的变化，如图4所示。矢量在切平面上的变化，就是几何分析中的协变导数。

图4 矢量沿坐标线的平移

协变导数的定义为：不考虑矢量在垂直切平面方向上的变化，只考虑在切平面内的变化，定义e1在u1方向的协变导数为

从图4看到

式(8)可以写为

e1为切平面上的切矢量，u1为曲面坐标，Γ为克里斯托费尔符号(克氏符)。考虑e1在u2方向以及e2在u1，u2方向的移动，可以写成统一形式

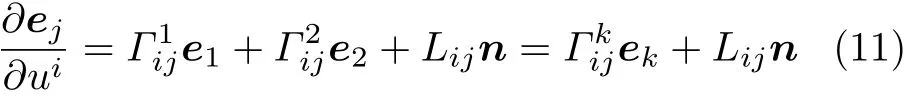
式(11)的第二个等式采用了爱因斯坦求和约定，上下相同的角标代表在所有维度上求和。的三个角标可以考虑如下：i角标为沿该坐标线平移，j角标为平移的那一个切矢量，上角标k为在该切矢量上的投影。

切平面上的任意矢量可以表示为

该矢量的协变导数可以写为

式(13)去掉了在曲面垂直方向的分量，给出了矢量在切平面内的变化，即协变导数给出了二维生物在曲面上运动时感受到的加速度。如果计算出曲面上的克氏符，就可以通过式(13)给出任意矢量沿不同坐标的协变导数，即给出沿坐标线的加速度。下面给出计算克氏符的过程，由式(11)有

其中

gkl为度规张量矩阵。式(14)两边乘以度规张量矩阵的逆矩阵，就可以求出曲面的克氏符。

下面给出傅科摆摆球速度矢量在球面固定纬度上平移即协变导数为零时需要满足的方程。球面上的坐标如图5所示，球面上一点的矢径可以写为

图5 球面上的坐标与切平面上的切矢量

取u1=φ和u2=θ，故球面上的切矢量为

为了后续计算方便，改写为单位矢量度规张量矩阵和其逆矩阵为

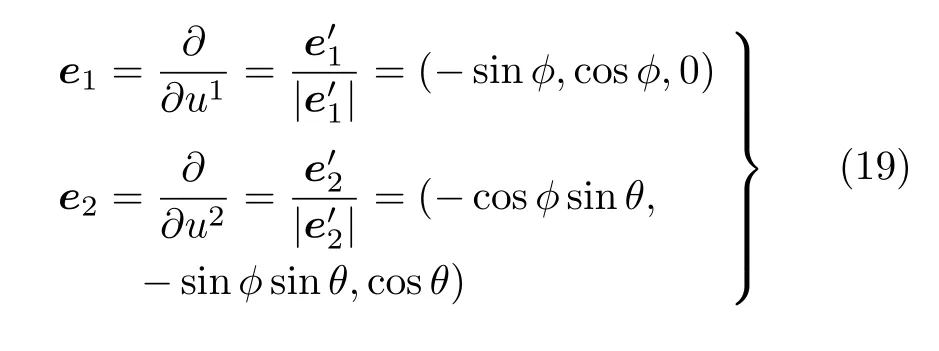
如果速度矢量在切平面内没有变化，意味着二维生物感受到的加速度为零，即沿u1方向的协变导数为零

协变导数为零，则两个分量必须为零，有如下方程

该方程简写为

考虑到这是一个线性系统，参考线性控制理论的结论[16]，如果矩阵A有k个实数特征值，2s个复特征值，式(24)的解为

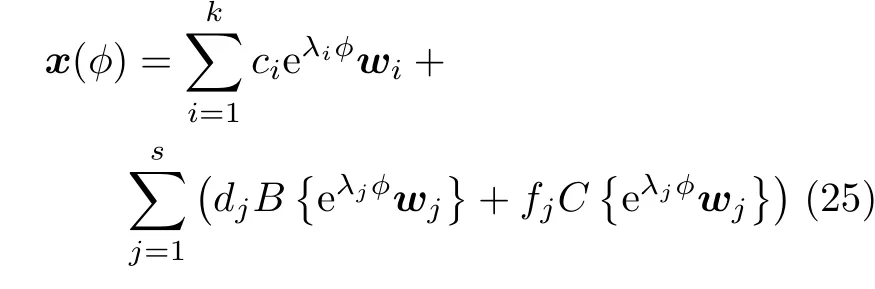
式中，ci，dj，fj为常数；wi为实特征值对应的特征向量；wj为复特征值对应的特征向量；B为取实部；C为取虚部；λi为实特征值；λj为复特征值。

矩阵A的特征值为 (-isinθ，isinθ)，特征向量为 (1，-i)T，(1，i)T，故有比较图5和图2的坐标系，任意矢量的分量取v1=x，v2=y，故方程(23)的解为

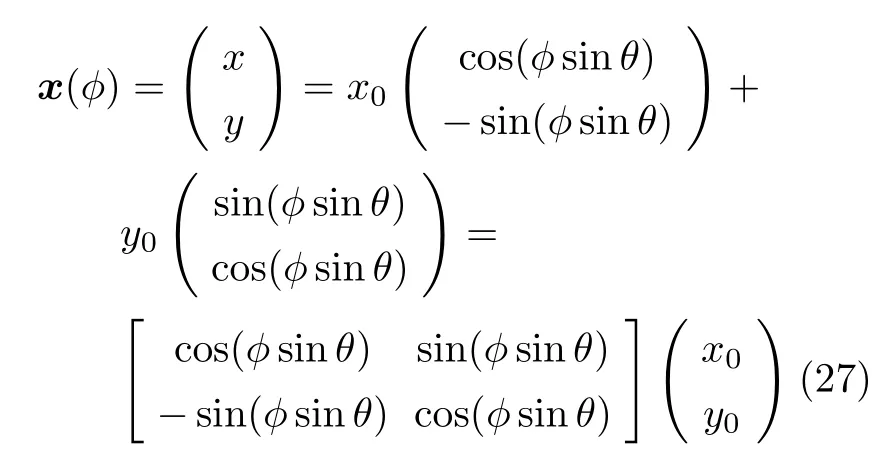
x0和y0为初始值。比较式(27)和式(7)可以得到

即Ωt=φ，这说明几何方法和牛顿力学方法的解是完全相同的。

几何方法说明傅科摆摆平面转动的原因是由于垂直摆平面的方向不受任何力，摆球速度矢量要在球面的切平面上平移，而速度矢量平移的结果就是摆平面要发生转动。

4 傅科摆的几何分析和牛顿力学方法之间的联系

4.1 采用几何法反推牛顿力学方程

虽然几何法给出了和牛顿力学方法同样的解，但是几何方法没有给出傅科摆的牛顿力学方程。因此，本文利用式(27)的解进行反推，推导出摆平面以角速度Ωz转动时的动力学方程。欧式空间静止的局部坐标系为 (t，x0，y0，z0)，摆平面转动时局部坐标系相对静止坐标系的旋转如图6所示，可以给出坐标变换的公式

式中，Ωz为绕z轴的角速度。

设矢量场X=xi(∂/∂qi)，Y=yj(∂/∂qj)，Z=zk(∂/∂qk)；f，g为普通函数，根据协变导数的定义式(13)，容易证明

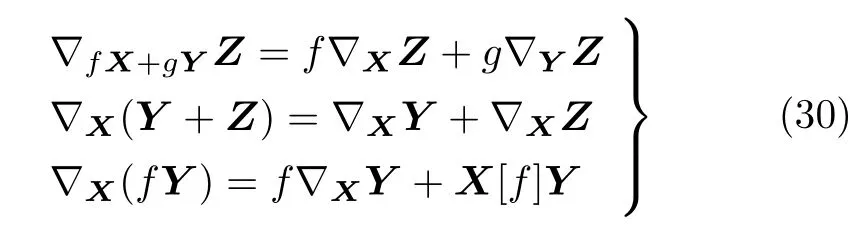
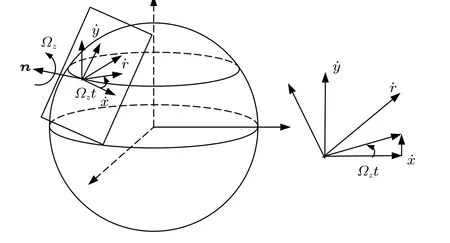
图6 旋转坐标系下的加速度分析

根据式 (30)，可以得到协变导数在不同坐标系下变化规律为

由式(15)知，欧式空间的度规张量矩阵为单位矩阵，则所有，并且由式(29)得到

其逆矩阵为

根据式(32)求出中不为零的克氏符号为

设粒子运动时的轨迹为c(t)=(q1(t)，q2(t)，···，qn(t))，切矢量为

切矢量沿曲线方向的协变导数为处于静止坐标系时，由牛顿定律写出单摆的运动方程为

-ω2x和-ω2y分别为摆球在坐标方向的受力，则方程(35)可以写为

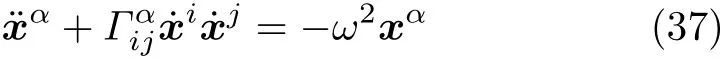
代入式(32)求出不为零的，写成分量形式为

式中，项为离心力，由于地球自转的角速度远小于单摆的角频率，因此舍去该项，式(38)变为

式(39)和牛顿力学方法给出的式(4)完全一样，因此几何方法和牛顿力学方法是等价的。

4.2 结合球面上的矢量平移推导牛顿力学方程

为了更直观理解傅科摆的运动，分析如图6所示，傅科摆摆球在地球上的矢径为r，摆球的运动速度为

根据式(22)给出矢量沿固定纬度的协变导数为

这时取v为速度矢量

式(40)可以改写为

式(42)只考虑了摆球的加速度沿着e1和e2方向，而没有考虑e1和e2随时间的变化，下面考虑e1随时间的变化。从图6可以看到，由于地球转动，e1的变化沿y方向，大小为

同样e2的变化沿x的负方向，大小为

考虑到φ=Ωt，式 (42)的各分量要乘以Ω才能得到对时间的导数，进而得到在切平面的加速度。式(42)和式(44)结合，给出沿x方向的加速度为

同样沿y方向的加速度为

不考虑离心力，仅考虑摆球在坐标方向的受力为-ω2x和-ω2y，式 (45)和式 (46)变为

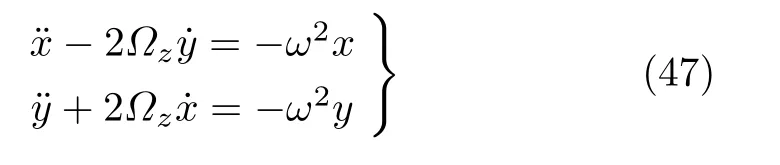
式 (47)仍和牛顿力学方法给出的式 (4)完全一样，并且矢量平移描述的方法更加直观。

5 结论

在傅科摆的研究中，由于几何法不考虑动坐标系为非惯性坐标系下的科里奥利力，因此避免了在特定条件下确定科里奥利力，与牛顿力学方法相比几何法显得更加简洁和抽象。几何方法说明，傅科摆摆平面转动的原因是在球面上平移速度矢量的结果。本文采用几何法和牛顿力学法推导出的运动方程以及方程的解完全相同，证明了两种方法是等价的。