宽带多普勒测速技术中跨周期模糊问题的研究

王俊宇，景永刚，许伟杰

(1.中国科学院声学研究所东海研究站，上海 201815；2.中国科学院大学，北京 100049)

0 引 言

声学多普勒流速剖面仪(Acoustic Doppler Current Profile, ADCP)，是一种利用相位编码调制脉冲技术，向各水层发射多个调制脉冲信号，并接收其反射回波脉冲，再通过复相关测频算法计算各水层对应相干脉冲的多普勒频偏值，进而精确计算出各水层流速值的测速仪器。假设通过换能器向水中发射频率为f0的声脉冲信号，该信号在经过各水层散射体的散射以及海底边界的反射后，将损失一部分能量，而由换能器接收到的脉冲信号，经过一定的处理之后可以计算出回波脉冲的频率f1。根据多普勒原理，当声源与散射体之间具有相对运动的时候，f0≠f1，并且存在以下关系：

其中：fd为多普勒频偏，v为换能器与水中散射体的径向相对速度，c为水中声速，α为发射波束与海底平面的夹角。

宽带声学多普勒流速剖面仪(Broadband Acoustic Doppler Current Profile, BBADCP)，在发射声脉冲时，使用双相(0°和 180°)伪随机编码对其进行相位调制。接收回波脉冲时，利用两个正交的本振信号，分别与接收的回波信号进行解调运算，再通过低通滤波器获得两路正交信号，之后利用复相关测频算法可以计算出对应的多普勒频移，进而可精确测量各水层流速[1]。

在复相关测频算法中，存在测速模糊的问题，即调制脉冲的宽度与所能测量的流速范围存在反比关系。文献[2]中利用时延估计确定复相关测频的模糊区间，这样不可避免地会产生时延估计误差，并且为了保证时延估计误差的精度，需选择高精度的时延估计方法，对采样率和运算量产生更高的要求。本文在此基础上，利用长脉冲信号(重复的短脉冲对)进行测量，结合长短脉冲信号各自的特点，将短编码脉冲信号所测频偏结果作为判别标准，确定长脉冲信号的模糊区间。该方法计算量小，对采样率的要求不高，并且能够在保证较高精度的前提下，完成测速工作。

1 复相关算法

1.1 BBADCP回波脉冲信号处理

在BBADCP中，假设接收回波脉冲sr设为

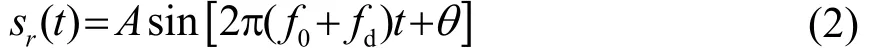
式中：A为回波脉冲的幅值，f0为发射脉冲的中心频率，fd为产生的多普勒频移，θ为发射脉冲的初始相位。之后可以利用两个正交的本振信号对回波脉冲进行正交解调处理，获得I/Q两路实信号，正交解调的过程如图1所示[3]。

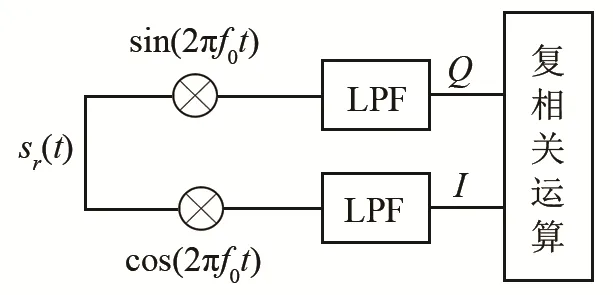
图1 回波脉冲的正交解调过程Fig.1 Quadrature demodulation process of echo pulse

回波脉冲信号的正交解调，即混频过程之后，设计低通滤波器对信号进行滤波，作用是滤掉信号中的高频成分。在滤波完成之后得到信号的同相分量I以及正交分量Q：

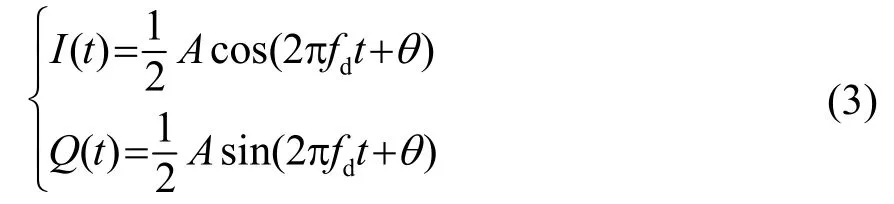
将I/Q两路实信号组合成一个复信号Z(t)，根据采样定理对其采样获得离散信号Zn：

其中：In、Qn为I(t)、Q(t)采样后的离散信号。利用采样后得到的信号计算其复相关函数R(h)，则有[4]：

式中：h是用整形采样数表示的时延，一般情况下，该时延等于所选脉冲信号的长度，N为采样后得到的离散数据点数。即得到：

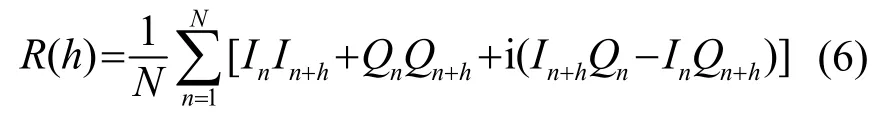
根据多普勒频移计算公式：

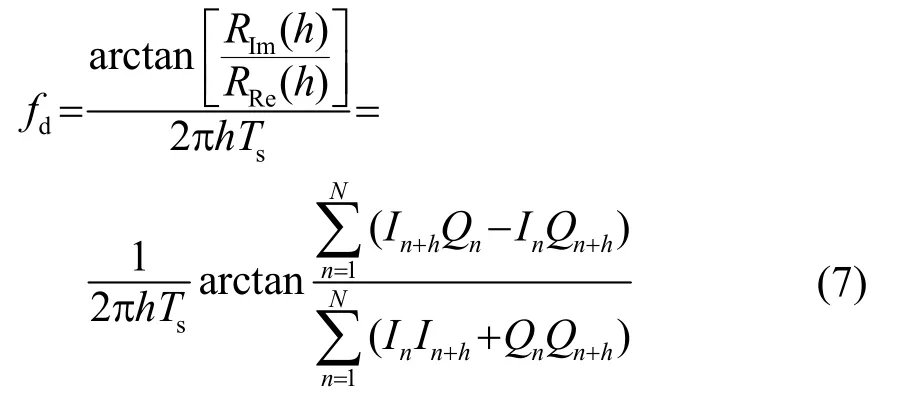
式(7)中：Ts为采样间隔，所求得的fd为回波脉冲与发射脉冲中心频率的偏差值，即多普勒频移，进而可以计算出对应水层的流速[5]。通过以上推导，可以看出复相关法测频的运算量较小，式(7)中仅需要做4N+2次乘法、2N次加法以及一次反正切运算。

1.2 测速精度

因为 BBADCP发射的是由伪随机编码调制的脉冲信号，所以在对回波脉冲进行处理时，需要使用一定长度的脉冲间隔分割信号，即对回波信号在不同深度上分层，并且脉冲间隔的大小应与分层后所得深度单元的大小相同。

由于利用伪随机码对脉冲信号进行编码之后，每一个编码码元的测量值将是独立的，因此，BBADCP按照所使用伪随机码的码元个数，继续将每一个深度单元分割成与码元个数相等的多个小层，每一个小层获得一个流速，之后对该深度单元中所有获得的流速进行统计平均，所得均值即为该深度单元的流速[6]。

因此，伪随机编码信号的码元个数越多，最后所得的速度均值越准确，即测速精度越高。

1.3 模糊问题的产生

对于式(7)，因为反正切函数的性质，复相关测频结果fd被限制于：

记fmax=1/(2hTs)为最大模糊频率，而换能器与水中散射体之间的径向流速V由式(9)可得：

式中：c为水中声速，fd为多普勒频移，f0为发射脉冲中心频率。因此，结合式(8)和式(9)可得径向流速的测量范围为

由式(10)可以看出，相关时延h越大，所测流速范围越小，但随着相关时延的增加，脉冲宽度也随之增长，测速精度则越高。因此，当所测水流的实际速度超过所允许测量的最大有效速度时，就会导致测速结果不准确，在复相关测频算法中表现为跨周期速度模糊的现象。

2 伪随机编码信号性质

同样，由式(8)可以发现，运用复相关测频法所测得的频率值与相关时延h有关，而相关时延的选择受到发射脉冲调制信号的编码所控制，编码信号的长度可以决定相关时延的大小。

对于发射脉冲信号所选用的编码形式，原则是根据实际环境情况来获取回波脉冲信号尖锐的自相关主峰和最小的自相关旁瓣。因此，对于所使用的m序列伪随机码而言，分别研究长度为15阶与4×15阶的自相关函数，如图1所示。

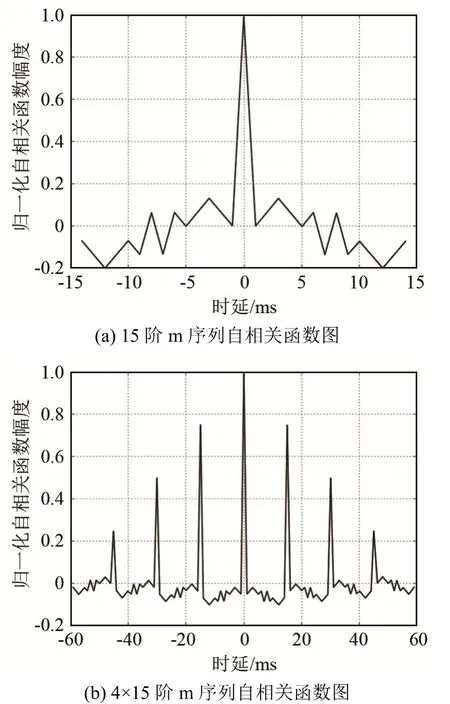
图2 不同长度m码序列的自相关函数图Fig.2 Autocorrelation function graphs of the m code sequence of different lengths

由图2可以看出，m序列越长，其自相关性能越好。而经过 m序列调制后的发射脉冲信号(正弦脉冲信号)，其频谱也在中心频率(600 kHz)处出现主峰值[6]。如图3所示。

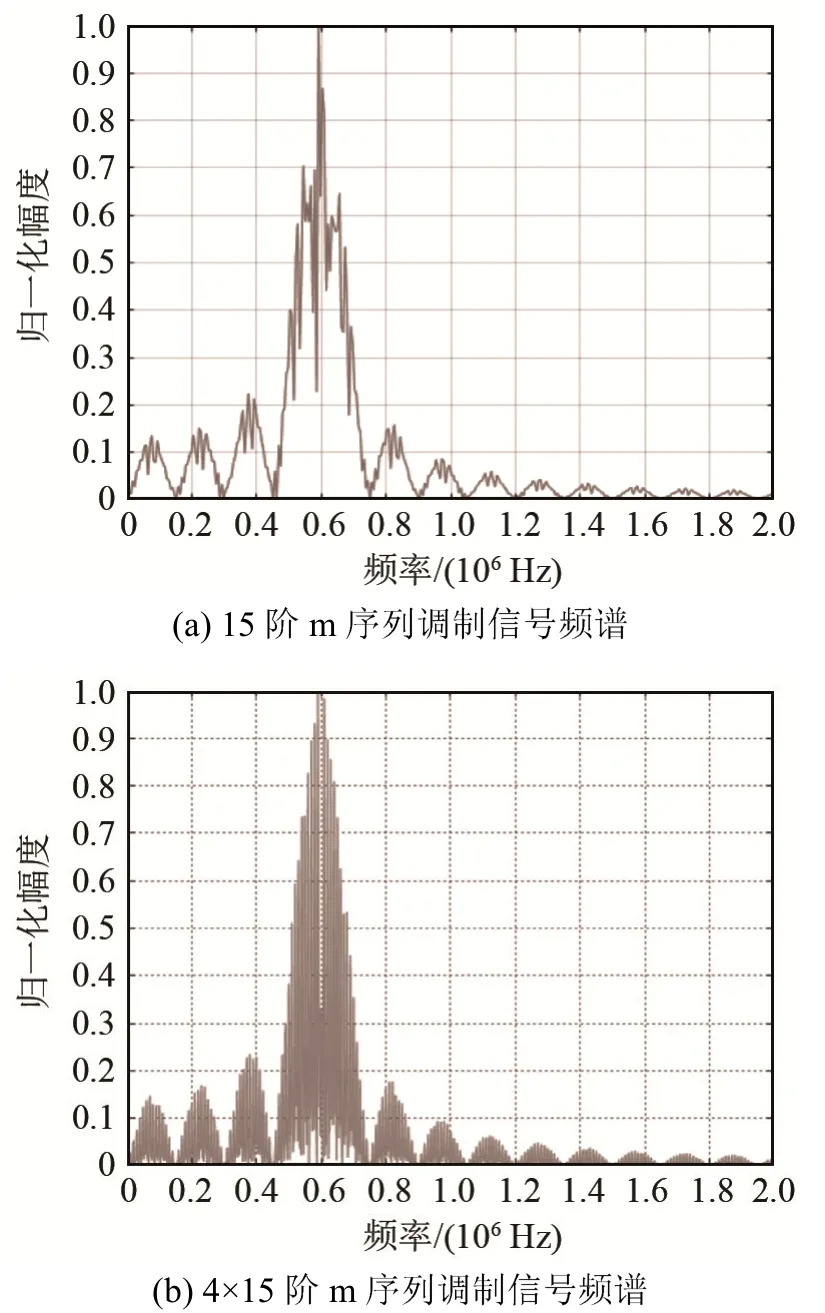
图3 不同长度m码序列调制脉冲的频谱Fig.3 Frequency spectrums of the pulse signal modulated by the m code sequence of different lengths

因此，就理论而言，伪随机编码信号的长度越长，其相关主峰越尖锐，说明其相关特性越好，则在对回波脉冲进行采样处理时，来自各个码元的回波信号将会具有较强的独立性，并且在测量单一水层流速时，测速精度也将越高。但是，随着码元数的增多，编码脉冲信号的长度也随之增加，所能准确测量流速的最大值也相应地减小。

3 长短编码信号选取

在实际测速过程中，实际水流速度的大小是未知的，所以在使用复相关测频算法测速时，会存在测速模糊的可能性，并且，若是为了获得更高的测速精度，则会需要选择较长的编码脉冲信号，但随之所能测速的有效范围会很窄。

设所使用的编码调制信号产生的最大模糊频率为fmax，由式(8)可以发现，复相关法测频方法所得的测频结果呈周期性变化，如图4所示。

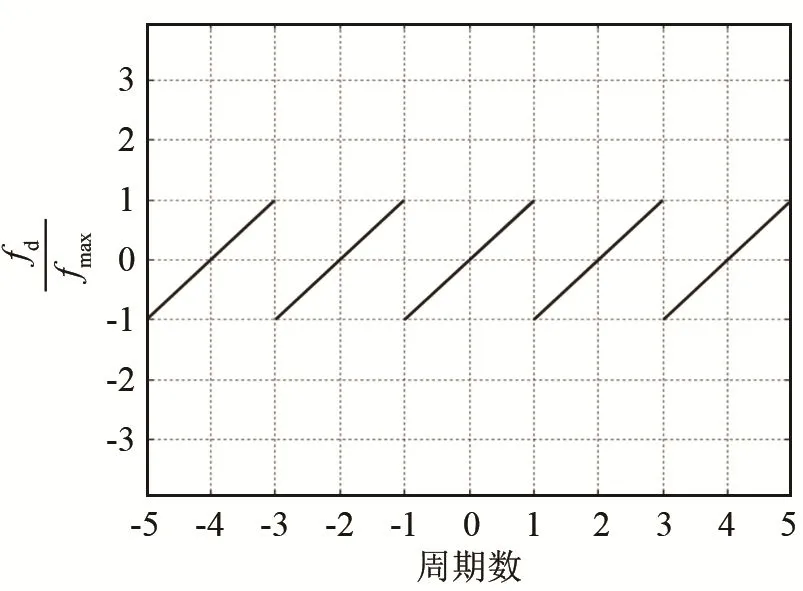
图4 复相关测频偏差的周期性变化图Fig.4 Periodic variation diagram of frequency measurement deviation based on complex correlation

由图4可以看出，复相关法测频结果呈现周期性变化，在超过某一区间的临界值(模糊频率)时，所测结果将由正值变为负值，并继续按照线性变化呈现下一周期的测量结果[2]。

在实际测量时，长编码脉冲信号所能测得的fmax值比短编码脉冲信号的小，但其精度比短编码脉冲信号高。因此，可以先用短脉冲信号在不产生模糊的情况下测出频移的粗略值，再通过长脉冲信号测出一个待定值fd，这个待定值不确定是否模糊，假设其为不模糊的准确频移值，结合图4和式(11)将该值在每一周期内的对应值fd'计算出来：

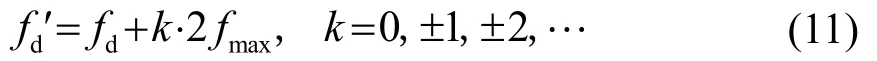
式中：fd为长脉冲信号测出的待定值，k是对应的周期数。之后与短脉冲信号所测粗略值进行对比分析，选取差值最小的一个对应值作为长脉冲信号的测频结果，如图5所示。

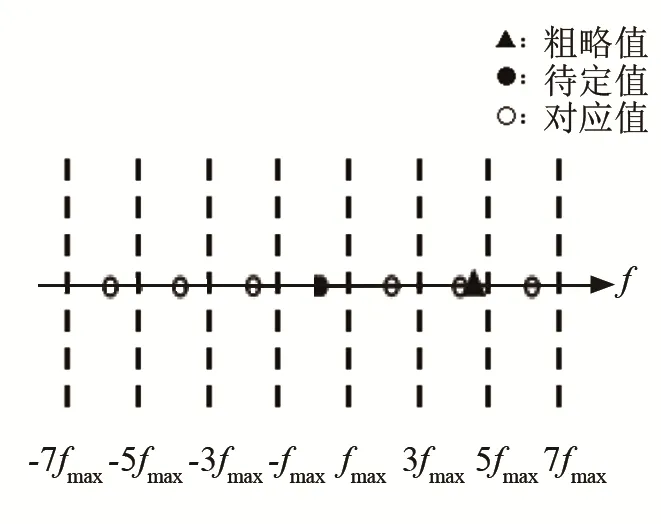
图5 长和短m编码调制脉冲结合的复相关测频法去除频率模糊的图解说明Fig.5 A graphical description of frequency-ambiguity removal for the complex-correlation frequency measurement method combined with long and short m-coded modulation pulses

在实际应用中，发射一段由多个低阶编码脉冲重复合成的长编码脉冲进行测频，在接收脉冲中，取该重复脉冲的第一段低阶短编码估算频偏的范围，之后再利用整段长脉冲结合上述方法计算频偏的精确值。通过该方法计算出的频偏值由于是利用多段低阶编码合成长脉冲编码调制信号后所得，因此具有较高的精度，并且在较低信噪比的情形下，也有较高的精度及准确性。

4 回波信号处理仿真

由上文可知，m序列长度越长，自相关性能越好，但在实际中还需考虑环境噪声以及信号带宽等因素的影响，综合选取调制编码的码元数。

假设发射脉冲的中心频率为 600 kHz，发射脉冲的初始相位设为180°，为方便与63阶m序列进行比较分析，所使用的长短m序列长度分别为15阶以及4×15阶，每段编码序列重复2次形成相干脉冲对，每段编码中，一个码元宽度填充4个周期的正弦波，回波信号的采样率设为中心频率的 10倍，低通滤波器的带宽为 400 kHz，信噪比为20 dB。整个回波脉冲仿真处理流程图如图6所示。

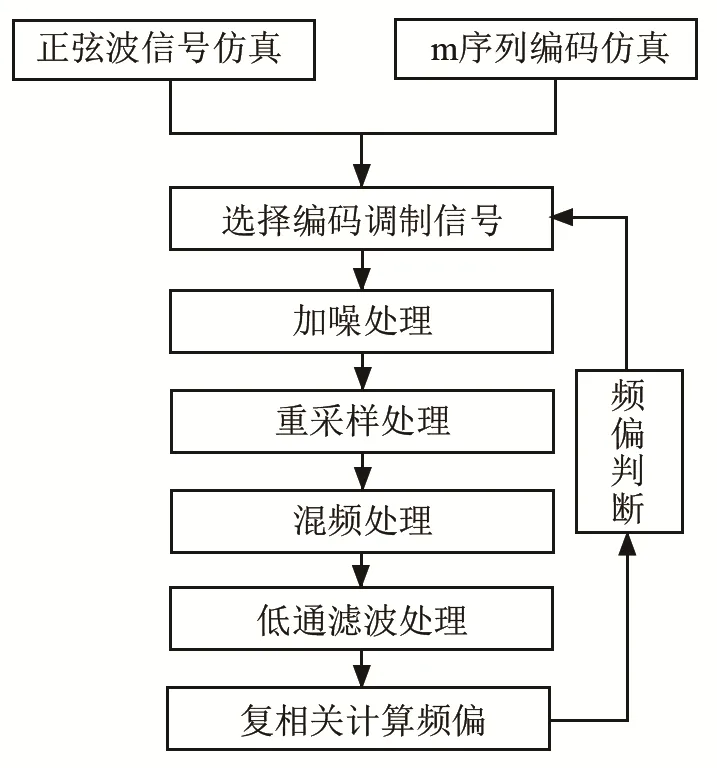
图6 仿真回波信号处理的流程图Fig.6 Flow chart of simulating echo signal processing

根据图6中的流程图，最后仿真处理结果如图7所示。

图7显示了不同长度的编码调制脉冲，利用复相关算法所仿真得到的模糊测频结果。由图7可以看出，所用调制编码信号的序列长度越短，其所能测出的有效多普勒频移范围越宽。另一方面，在两者均不产生模糊频率的情况下，对比两者所测频偏的精度如图8所示。

从图8可以看出，在均不产生模糊频率的前提下，4×15阶m序列的测频结果波动范围比15阶m序列的测频结果波动范围小，所以 m序列的长度越长，测频精度也越高。

在实际测量中，低信噪比环境下的测流精度要求较高。利用上述方法构造4×15阶的长编码脉冲信号，并在5 dB的低信噪比条件下进行测频，获得的结果如图9所示。

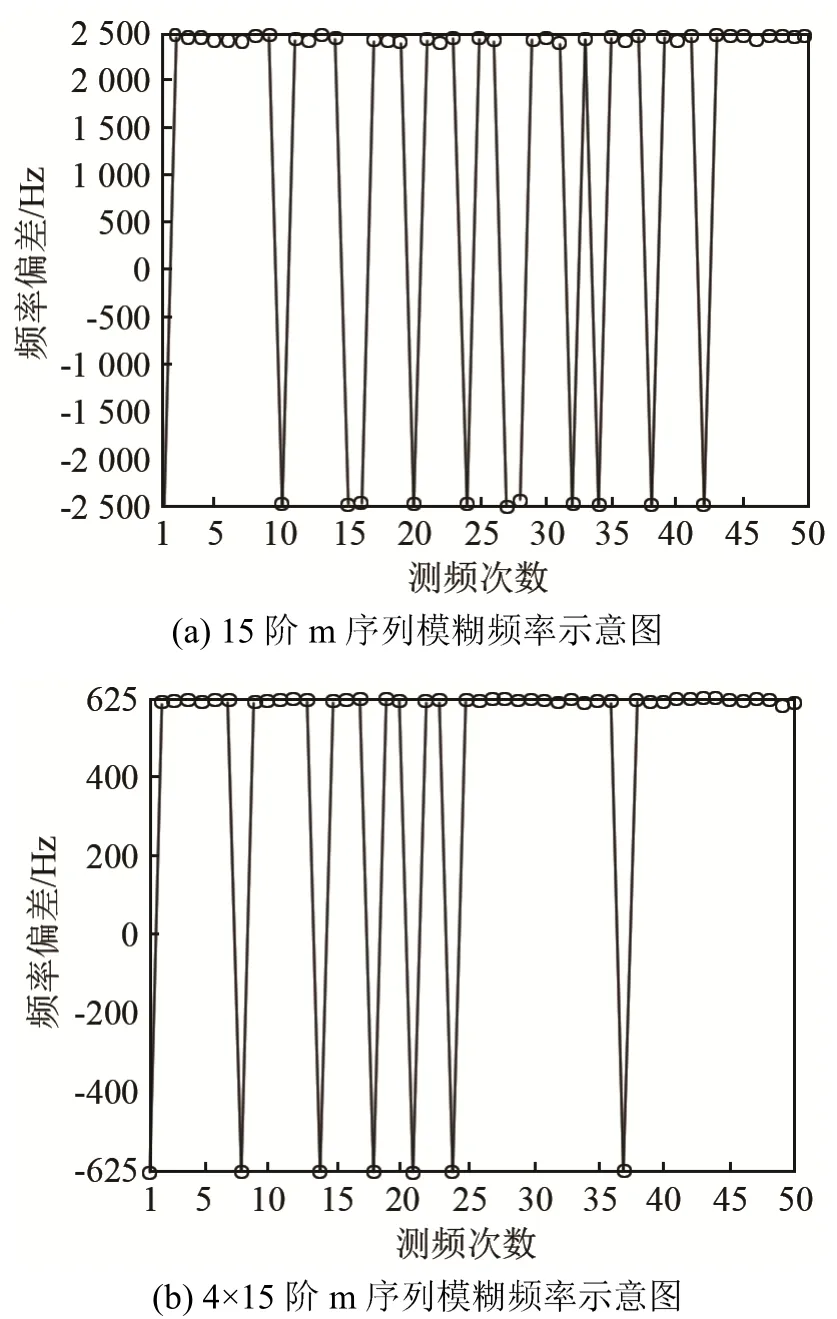
图7 不同长度m编码调制脉冲的模糊频率示意图Fig.7 The ambiguous frequency diagrams of the m coded modulation pulses of different length

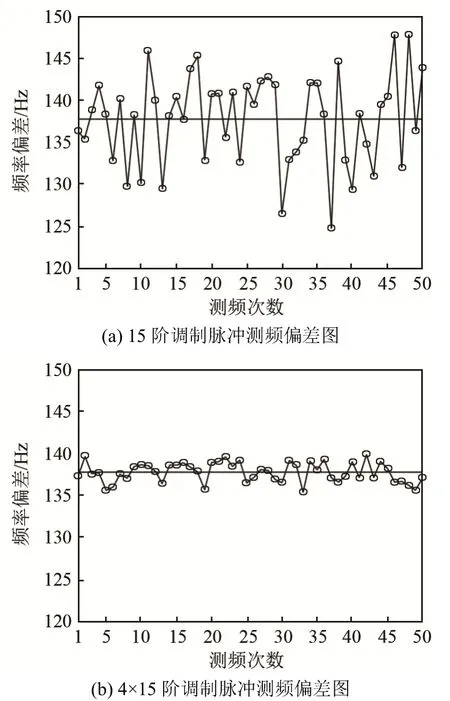
图8 不同长度m编码调制脉冲的测频偏差图Fig.8 The frequency measurement deviation diagrams of the m code modulation pulses of different lengths

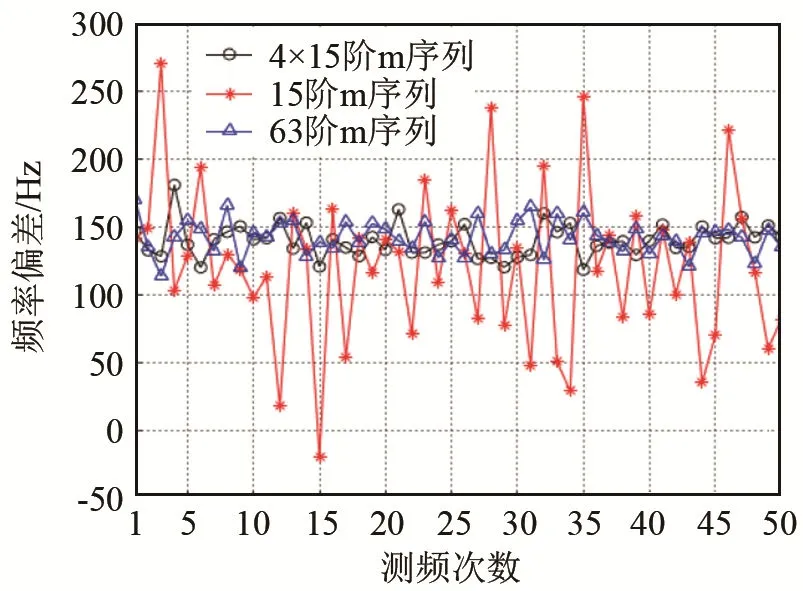
图9 低信噪比下不同长度m编码调制脉冲的测频偏差图Fig.9 The frequency measurement deviation diagram of the m code modulation pulses of different lengths at low signalto-noise ratio

从图9可以看出，4×15阶m序列与63阶m序列的测频结果波动程度相近似，即在低信噪比环境下依然有较高且较为稳定的测频精度，而15阶的短编码脉冲俨然出现了“测不准”的现象，即测频误差太大，无法使用。所以，在需要较好解决测速模糊的前提下，应尽可能使用长的编码序列进行测频。

另外，在高速测流环境下，针对其容易产生的速度模糊问题，结合式(11)来解决，通过仿真可以得到，长和短m编码调制脉冲结合的测频偏差如图10所示。

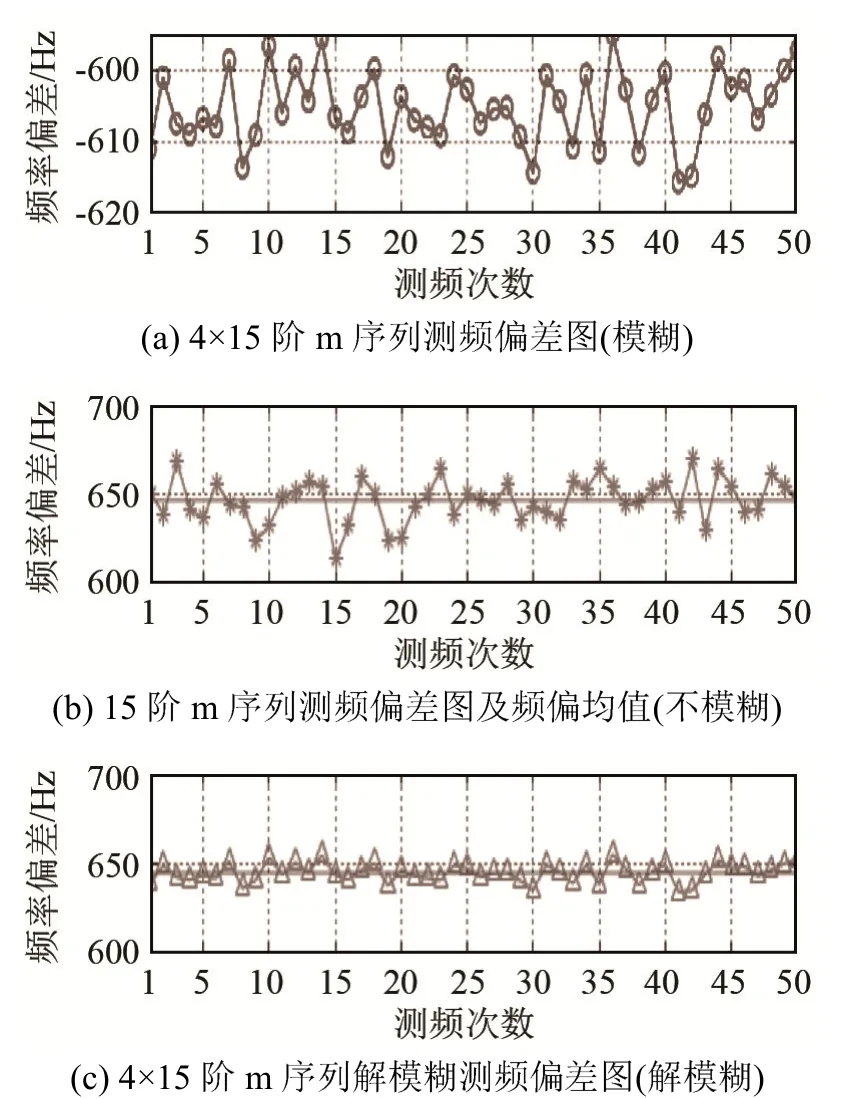
图10 长和短m编码调制脉冲结合的测频偏差图Fig.10 The frequency measurement deviation diagram of the combination of long and short m code modulation pulses

由图10可以看出，利用4×15阶m序列调制信号进行测频时，出现频率模糊的情况可以由本文所运用的方法较好地实现跨周期测频的目的。并且从图中也可以发现，4×15阶m序列的解模糊测频结果比15阶长度的m序列测频结果的波动范围小，即测频精度得到一定程度上的提高。

5 结 论

本文在 BBADCP发射脉冲信号的编码调制选择上，结合了长短编码脉冲信号在宽带多普勒测流中各自的优势，利用短脉冲信号重复构造出相应的长脉冲编码信号，并将其测频均值作为长脉冲信号选择模糊区间的判别标准，在不损失精度的前提下，较好地解决了在使用复相关测频算法时引起的跨周期测频模糊问题，并且在较低信噪比时，也能有较好的测频精度。