海洋中持续泄漏气泡的声学检测

侯 森，胡长青

(1.中国科学院声学研究所东海研究站，上海 201815；2.中国科学院大学，北京 100049)

0 引 言

气体泄漏广泛存在于海洋环境之中，其中海底甲烷水合物自然泄漏及相关开采运输造成的泄漏，往往都具有长时间持续泄漏的特征，不仅会造成经济损失，更容易引发安全和环境问题[1-3]。依据泄漏气泡产生的声学信号作为检测识别方法，具有易于实现、适用性强等特点。

为了实现在实际海洋环境中对气体泄漏的声学检测，很多人对气泡声信号进行了研究。王鑫等[4]对气泡声发射信号进行了分类，并指出当泄漏量较小时，气泡声发射信号以振荡声为主。侯森等[5]基于水合物气泡泄漏时的物理特性，对泄漏气泡振荡特性进行了修正，计算了不同环境下泄漏气泡半径与能量和半径与频率的关系。杜非[6]指出海洋中持续性气泡泄漏具有较强的周期性和重复性，并研究了微量气泡泄漏时的声学特性。吴连军等[7]研究了微弱信号的提取方法，指出频域积累法可以有效提高窄带信号的信噪比。此外，还有很多人对微弱声信号的提取和检测做出了研究[8-10]。

为了解决气泡信号容易被环境噪声遮蔽的问题，本文从气泡振荡特性的研究出发，采用了频域积累的方法进行降噪处理，并针对连续泄漏气泡具有强周期性的特点，通过一种基于时频分析的自适应检测算法，判别有无气泡声信号并对气泡振荡主频率进行检测。通过仿真和实验，验证了本文方法可以在较强干扰的环境中实现对持续泄漏气泡的检测、判别。

1 泄漏气泡声学特性

1.1 气泡动力学模型

当泄漏量较小时，持续泄漏气泡的声信号主要由气泡振荡产生[4]。在构建气泡振荡模型时，做了以下假设：气泡为理想球形、液体不可压缩、忽略海流等因素引起的压力场变化并忽略泡内蒸气压。同时在模型中考虑了液体黏性以及气泡内气体非理想时对气泡振荡的影响。气泡内压强为

其中：P0为环境压强，R0为气泡平衡半径；Pi0为气泡平衡时的内部压强；σ为张力系数。考虑到实际气泡内为非理想气体，引入描述气泡可压缩性的系数β进行修正[5]，则任意时刻下的气体状态方程如式(2)所示：

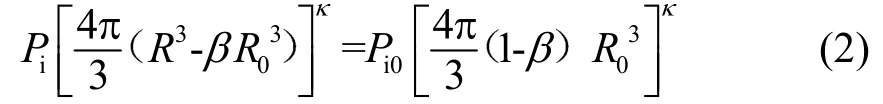
其中：Pi为任意时刻的气体内部压强，R为任意时刻下的气泡半径大小，κ为多方指数。引入粘滞系数u，则任意时刻下气泡外部压强Pout为

假设液体不可压缩，根据能量守恒定理，液体动能的增量等于气泡对液体所做的功，如式(4)所示：

由于式(5)难以求取解析解，本文通过四阶龙格库塔(Runge-kutta)算法进行了特定初值下的数值求解。设环境参数如下：P0=1.01×105Pa；β=0.1；ρ=1 000 kg·m-3；κ=1.4 ；σ=72×10-3N·m-1；u= 8×10-4Pa·s-1。气泡初始半径为平衡半径的 1.2倍，即Ri/R0=1.2。则不同半径气泡的振动如图 1所示，气泡在泄漏时获得初始能量，并围绕平衡半径做振荡衰减。从图 1中可以看出，气泡振动声信号单频特性明显，且能量衰减很快，环境一定时，气泡振荡频率随气泡半径增大而降低；气泡振幅则随气泡半径增大而增大。

图1 不同半径气泡振荡曲线Fig.1 Vibrations of bubbles with different radii

海洋环境中发生的泄漏通常具有持续性，并且有位置固定，压差、漏孔等参数在一定时间内稳定的特点[6]。故同一泄漏点产生的气泡往往具有气泡半径相近、泄漏气泡间隔相对恒定的特点。为模拟海洋环境中持续泄漏气泡的声信号，除采用上文的环境参数外，设生成气泡的平衡半径R0为1.3～1.8 mm间的随机值，气泡生成间隔为0.1 s。图 2所示是理想无噪声的连续气泡声信号，由于气泡能量衰减极快，在时域上表现为振动频率相近的一连串脉冲信号。而当环境噪声能量较强时，气泡声信号易被淹没。在加入信噪比为−10 dB的加性高斯噪声后，噪声背景下的气泡声信号如图 3所示，气泡声信号被环境噪声淹没。在强噪声干扰下，很难在时域上观察出气泡振荡引起的脉冲波形。

图2 无噪声干扰时持续泄漏气泡声信号Fig.2 Bubble sound signal without noise

图3 噪声背景下气泡声信号Fig.3 Bubble sound signal under noise background

1.2 频域积累

针对气泡声信号易被环境噪声淹没的问题，由于气泡声和环境噪声频段重叠，传统的滤波方法难以有效滤除噪声干扰。当气泡持续泄漏时，泄漏产生的声信号主要集中在一定频段范围内，采用频域积累的方法，可以使气泡声能量得到明显加强；而环境噪声的相关性差，经过频域累加后，其能量不容易被积累，故可以有效提高信噪比。频域积累法的主要步骤为：将待处理的信号x(n)分割成M段等长度的信号片段，依次将各信号片段做傅里叶变换并在频域进行累加，基于离散傅里叶变换的的频域累加公式为[12]

其中：xm(l)为第m段信号，L为离散傅里叶变换的点数，表示旋转因子，X(L)为傅里叶变换后的频域信号。将经过频域积累后的X(L)进行反傅里叶变换即可得重构的时域信号波形。对图3进行频域积累降噪处理，重构后的时域信号如图4所示。

由图4和图2的对比可以看出，经过频域积累处理，重构后的声信号可以较好地还原出原信号的时域波形，脉冲峰的间隔及振荡幅值等信息得到了较好保留。由图4和图3的对比可以看出，图4中信号的信噪比有明显的提升，且降噪效果随频域积累次数的增加而提升。

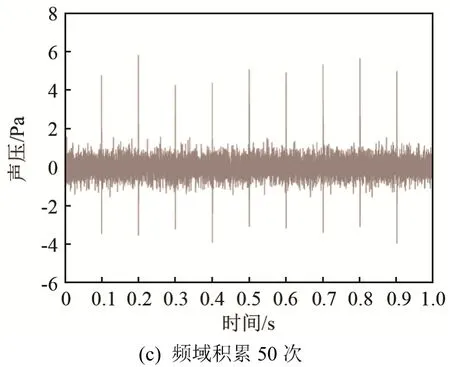
图4 基于频域积累法降噪处理Fig.4 Noise reduction based on frequency domain accumulation

1.3 时频分析

对频域积累前后的声信号做时频分析，如图 5所示。图5(a)为图3中信号的时频图，从图中可以看出，当加入宽带强噪声干扰后，在时频图中难以分辨气泡声信号。图5(b)为图4(c)中信号的时频分析，从图中可以看出，进行 50次频域积累处理后，信噪比明显提高，同时气泡的振荡频率以及泄漏时间间隔等信息保留较好。

图5 频域积累前后时频分析Fig.5 Time-frequency analyses before and after frequency domain accumulation

从图5(b)中可以看出，气泡声信号叠加噪声的模型中，能量随时间的变化在不同的频段处有明显的差异，为此对图5(b)进行了展开讨论，图6和图7分析了不同频段处的能量变化规律。图6(a)为气泡振荡主频段处的时间-能量变化图，由于持续泄漏气泡具有很强的重复性，所以在能量变化上表现出了强周期性。为了描述能量的周期性变化，对时间-能量曲线做了频谱分析，结果如图6(b)所示，时间-能量曲线的频谱具有明显的基频峰和谐波峰，基频和气泡泄漏时间间隔吻合。而非气泡振荡频段的能量变化如图 7所示，可以发现能量随时间的变化具有随机性，时间-能量的频谱中也没有基频峰和谐波峰的对应关系。所以检测特定频段下的能量变化规律可以作为气泡检测的依据，具体方法将在第2节中展开讨论。

图6 气泡声信号主频段处声信号能量随时间和频率的变化Fig.6 Variation of sound signal energy at bubble resonance frequencies with time and frequency

图7 低频段声信号能量随时间和频率的变化Fig.7 Variation of sound signal energy at low frequencies with time and frequency

2 实验数据处理

2020年项目组在某海域进行了海上实验。实验设计图如图8(a)所示，利用高压气泵向单孔导气管供气来模拟海洋中持续泄漏气泡，在出气口下方 1 m处布置水听器和温深仪(Temperature Depth,TD)，并选取了 4个深度测量气泡声信号数据。实验深度变化如图8(b)所示，分别在5.5、16.0、24.0和 36.5 m深度处进行了气泡声信号测量。自容式水听器和温深仪如图8(c)示。实验平台及供气气泵如图8(d)所示，实验过程中通过改变供气压强，保持实验过程压差基本恒定在0.45 MPa。

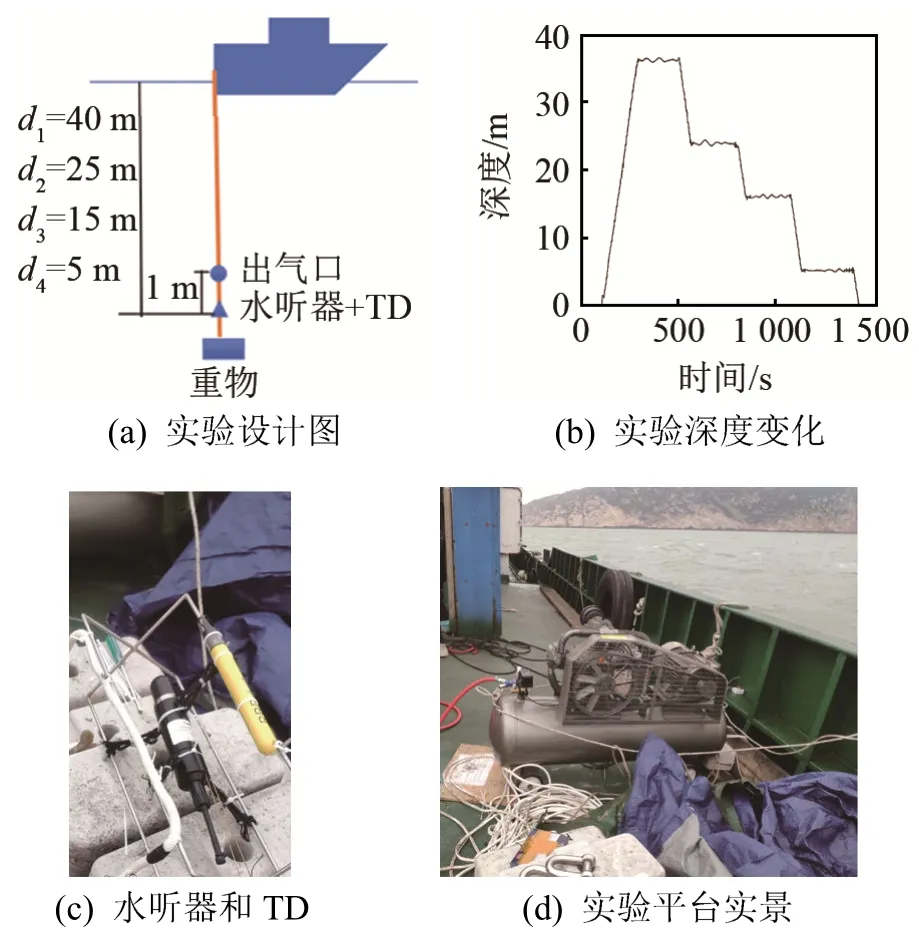
图8 实验场景简介Fig.8 Introduction to the experimental scene

以5.5 m处的声信号数据处理为例，经过滤波等预处理后，接收到的信号如图 9所示。由图 9可见，在实际海洋环境下，气泡信号被环境噪声完全淹没，很难观察到气泡信号特征。运用频域积累的方法进行 30次处理后，结果如图 10所示，从时域上看，信噪比有所提高，可以在部分时段见到气泡形成的脉冲峰，但噪声干扰依然严重。从图 11中的时频图上看，除了一些可能由气泡信号引起的亮点外，低频段的噪声干扰明显，较难区分出气泡信号的能量频段。由此可见，在非理想噪声环境下，频域积累方法结合传统的时频分析不能有效检测气泡声。

图9 预处理后海洋环境中声信号图Fig.9 Sound signal in marine environment after preprocessing

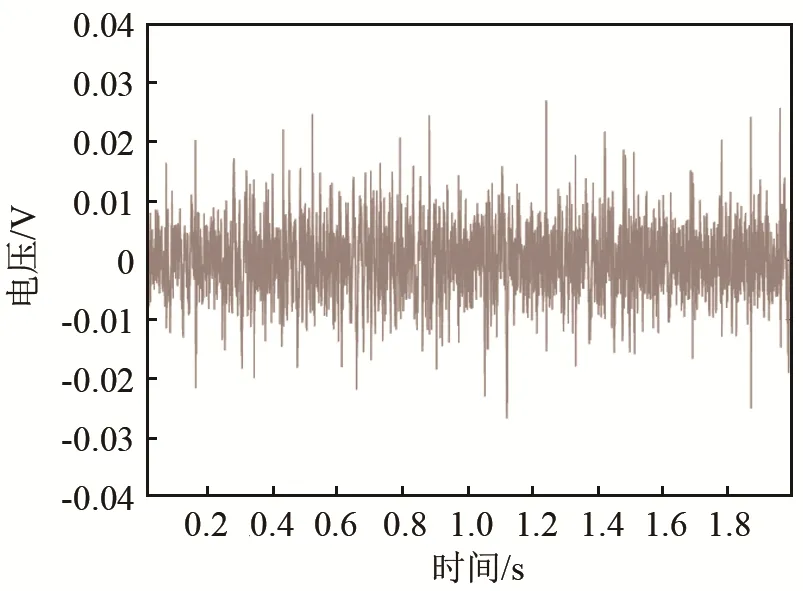
图10 频域积累后气泡声信号图Fig.10 The bubble sound signal after frequency domain accumulation

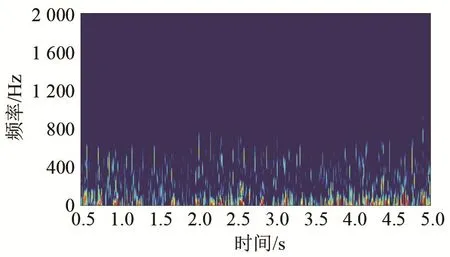
图11 频域积累后气泡时频图Fig.11 Time-frequency analysis of the bubble sound signal after frequency domain accumulation

为了在较强干扰下对气泡振荡频段进行检测，本文基于1.3节中的内容采用一种自适应检测算法对气泡声信号进行搜索判别。为了方便区分，下述算法中F表示声信号的频率，f表示为时间-能量频谱图中的频率。

(1) 假设Fi为待检测的声信号频率，计算声信号在Fi处的时间-能量变化关系并做频谱分析。对时间-能量曲线的频谱做归一化处理，并设[fmin,fmax]为搜索区间，进行峰值检测。

(2) 从低频峰开始遍历搜索区间内的峰值，将第一个峰值f0设为基频，并进行谐波检测。搜索[nf0−∆f,nf0+∆f]区间内是否存在对应的第n次谐波峰(n=1,2,⋅⋅,5)。若5次检测中存在3次以上谐波峰，则认为可能存在气泡并记录下来；若谐波峰少于3次，则记结果为空，更换基频f0重复此步骤，直到遍历搜索区间内所有峰值。若最后结果仍为空，则认为该频率Fi下无气泡。

(3) 对输出结果为可能存在气泡的频率值Fi进行结果检验。如果其邻近频段输出结果同样为可能存在气泡，则认为该频段为气泡振荡频率；如果邻近频段结果是无气泡，则认为Fi处的输出结果是虚警予以剔除。

图12 气泡声信号自适应检测流程图Fig.12 Flowchart of adaptive detection of bubble sound signal

上述检测算法流程如图12所示。其中考虑到步骤(2)中，基频f0的误差会给高次谐波检测带来较大影响，在每次检测到谐波后，对基频f0进行修正，修正公式为

其中：fn0为第n次谐波检测后对基频的修正值；fn为检测到的第n次谐波的频率。

根据声信号主要能量的频段范围，对频率F在0.1～1.5 kHz范围内的声信号进行了检测。设置参数如下：fmin=2 Hz，fmax=100 Hz，∆f=1 Hz。代入上述算法，对不同频率下有无气泡进行了检测。

不同频段处的声信号时间-能量及频谱变化如图 13、14所示。通过图 13可以发现，气泡振荡频段附近的时间-能量曲线，波形有较明显的周期性，时间-能量的频谱具有较为明显的基频峰和谐波峰，如图中箭头所指；而在噪声干扰较强的频段，如图 14所示，能量随时间变化没有明显的周期性，且其频谱无谐波特性。通过检测算法可以明显区分。

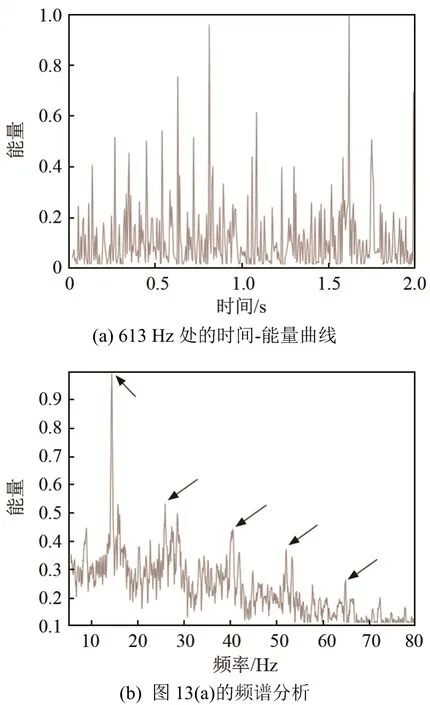
图13 存在气泡频段的声信号能量随时间和频率的变化Fig.13 Variation of sound signal energy at bubble resonance frequencies with time and frequency

图14 低频段处声信号的能量随时间和频率的变化Fig.14 Variation of sound signal energy at low frequencies with time and frequency

经过本文算法在不同深度下检测得到的气泡声频率如表1所示。表1中第二列为检测结果存在气泡的频段范围；第三列为第二列数据的中值，近似认为是气泡振荡的主频率；第四列数据为不同深度气泡声频率与5.5 m深处气泡频率的比值。Minneart[13]指出气泡频率是气泡半径和压强的函数。由于漏孔大小及内外压差恒定，不同深度的气泡半径仅由环境压强单一决定。故在本实验环境下，可以由不同深度下的环境压强经 Minneart频率公式计算得到频率比值，如表 1中第五列所示。通过表 1中数据可以看出，本文方法检测得到的气泡声频率随深度变化的趋势与理论值较为吻合，表明了本文方法在实际海洋环境中检测提取气泡声信号的有效性。

表1 不同深度下气泡声频率Table 1 Bubble sound frequencies at different depths

3 结 论

实际海洋环境中的泄漏气泡声信号，声能量较弱，频谱与其它环境噪声频谱重叠，传统方法较难将气泡声信号分离检测出来。本文首先通过频域积累的方法，进行了降噪处理，提高了信噪比。并在此基础上，基于持续泄漏气泡在气泡振荡主频段附近能量存在强周期性的特点，采用一种基于时频分析的自适应检测算法，对不同频率的声信号进行有无气泡声的检测，最后对所有频率检测结果进行汇总，得出气泡声的频段范围。对海上实验数据的处理表明，本文方法可以较好地实现对气泡声信号的检测和提取。