矩形板辐射体弯曲振动的轴向声场计算
2021-01-08贺西平
李 娜,贺西平
(1.陕西师范大学物理学与信息技术学院,陕西西安 710119;2.宁夏医科大学理学院,宁夏银川 750004)
0 引 言
由纵向振动换能器与弯曲振动辐射体组成的纵弯超声辐射系统,兼具纵振换能器大功率、高效率与弯振辐射体低辐射阻抗、大辐射面等特点,在超声悬浮、食品加工过程中的干燥和除泡、污泥处理、超声空气除尘等大功率气介质超声领域获得了应用[1]。
在弯曲振动辐射体辐射声场中,辐射体附近声压与质点速度不同相的区域称为近场,在该区域内辐射体轴向声压随与辐射体几何中心间距的增大有较大的、无规律的起伏变化。辐射体远处声压与质点速度同相时的声场称为远场,在该区域辐射体的轴向声压与距声源几何中心的距离成反比,即声压随轴向距离的增加而缓慢衰减[2-3]。实际应用中需要根据具体需求,选择恰当的工作区域。如近场悬浮技术,其工作机理是在换能器与被悬浮物体之间形成高强度声场,利用声场平衡被悬浮物自身的重力,使其被悬浮在一定的高度上,但是近场具有声压分布不均匀、起伏变化较大的特点,因此对于近场声压分布规律的研究显得尤为重要[4]。文献[5-7]中利用数值方法计算了活塞圆盘辐射体、固定及简支边界条件下的圆盘辐射体近场区域轴向声压,并对这三种辐射体的轴向声压进行了比较分析,为弯曲振动圆盘辐射体的应用提供了理论基础。Sadayuki等推导了平面圆盘弯曲振动所产生的近场声压分布的数学表达公式[8]。文献[9-12]中利用叠加法和高斯数值积分算法,计算了自由边界条件弯曲振动圆盘辐射体及具有比平圆盘辐射体指向性更加尖锐的阶梯圆盘辐射体的声场分布,并以二阶梯圆盘为例计算了其轴向声压随距离的变化关系,对设计的二阶梯、三阶梯和四阶梯圆盘的轴向声压进行了测试,验证了理论计算的正确性。
弯曲振动矩形辐射体的振动模式复杂,边界自由时没有解析解,但其振动模态中有节线平行于长边或宽边的条纹模态,与圆形弯振辐射体相比,处于条纹振动模态下的矩形辐射体的位移分布比较均匀[13-15]。本文利用数值方法结合有限元方法,推导了计算自由边界矩形板辐射体轴向声压的公式,该公式适用于任意形状平面状辐射声源,对阶梯厚度等于辐射介质中半波长的阶梯形辐射体也适用。
1 矩形板辐射体轴向声压计算
假设弯曲振动矩形板辐射体被嵌置在无限大刚性障板上。以辐射体上表面中心为坐标原点建立直角坐标系,如图1所示。
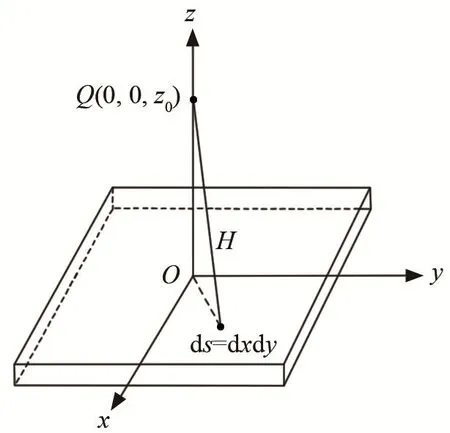
图1 辐射声场计算示意图Fig.1 Schematic diagram of radiation field calculation
辐射体向障板前面的空间辐射声场,观察点Q(0,0,z0)位于z坐标轴上,取辐射体表面某一微元ds(x,y,0),其面积ds=dxdy,则ds在Q点产生的声压为
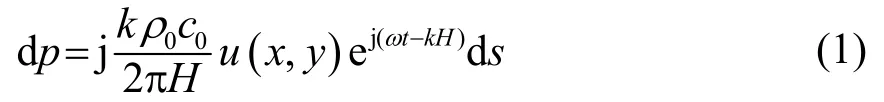
式中:H为ds与观察点Q之间的距离,;u(x,y)为ds的振速幅值。积分可得整个辐射体产生的辐射声压:
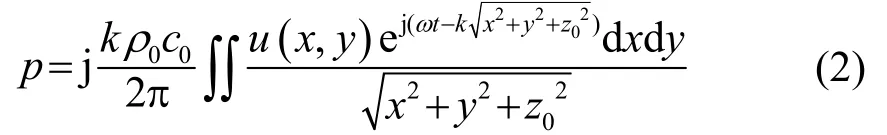
利用欧拉公式展开式(2)得:
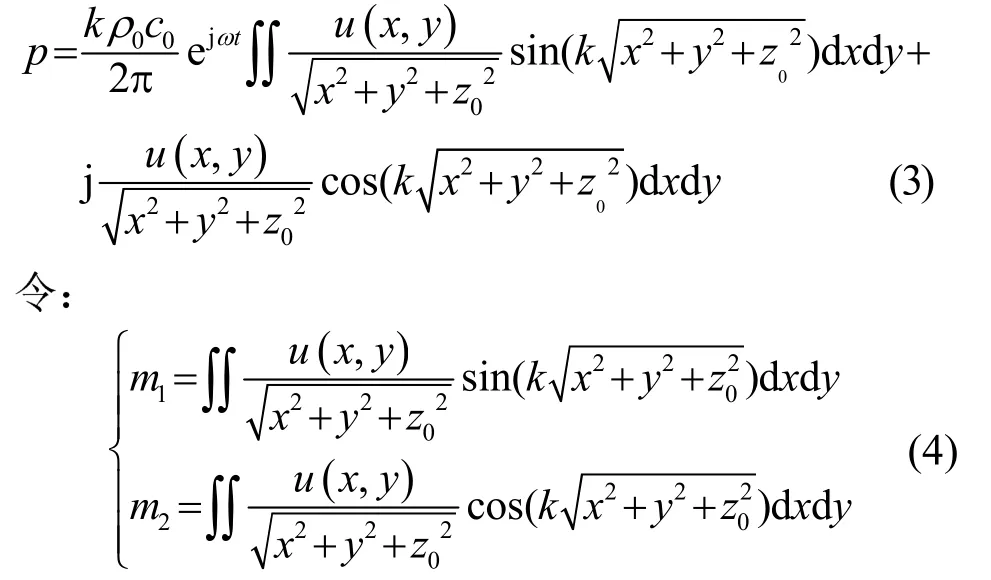
则辐射体产生的辐射声压可表示为

式中:ui,∆si分别表示第i个微元的振动速度及面积,xi,yi分别表示该微元的横坐标与纵坐标。利用ANSYS软件建立换能器中心激励矩形辐射体的有限元模型。选择辐射体的单元类型为SOLID187,将辐射体表面分为N个微元,有限元Modal模块计算出各微元的相对振动位移,根据任一微元振速ui与其位移ξi的关系:

将式(8)代入式(7),即可得到辐射体的轴向声压。
2 算 例
矩形阶梯体如图2所示。表1为矩形板辐射体几何参数。1#辐射体为平板辐射体,2#辐射体为阶梯辐射体。以表1所示几何尺寸1#辐射体为例(位移分布如图3所示),2#辐射体(结构如图2所示)是由1#辐射体在上述条纹振动模态下改进成的阶梯辐射体,其位移分布如图4所示(图中不同颜色表示不同的位移,ξmax表示位移最大,ξmin表示位移最小)。计算1#辐射板条纹振动模态下轴向声压与距离的关系,结果如图5(a)实线所示。计算得2#辐射板轴向声压与距离的关系如图5(b)实线所示。其中辐射体材料均为45#钢(泊松比v=0.28,杨氏模量E=1.96×1011N·m-2,密度ρ=7.91×103kg·m-3),f表示换能器与辐射体组成的振动系统的频率,N表示辐射体表面划分的微元个数。
由近远场临界点a2/λ可得(其中a表示矩形辐射体对角线长度,λ表示矩形辐射体在空气中辐射声波的波长),1#矩形平板辐射体近远场临界点距离矩形平板辐射体几何中心约 1.1 m,2#矩形阶梯辐射体近远场临界点距矩形平板辐射体约1.7 m。
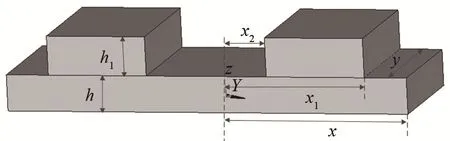
图2 矩形阶梯辐射体Fig.2 The stepped rectangular plate radiator

表1 两个不同矩形板辐射体参数Table 1 Parameters of two different rectangular plate radiators
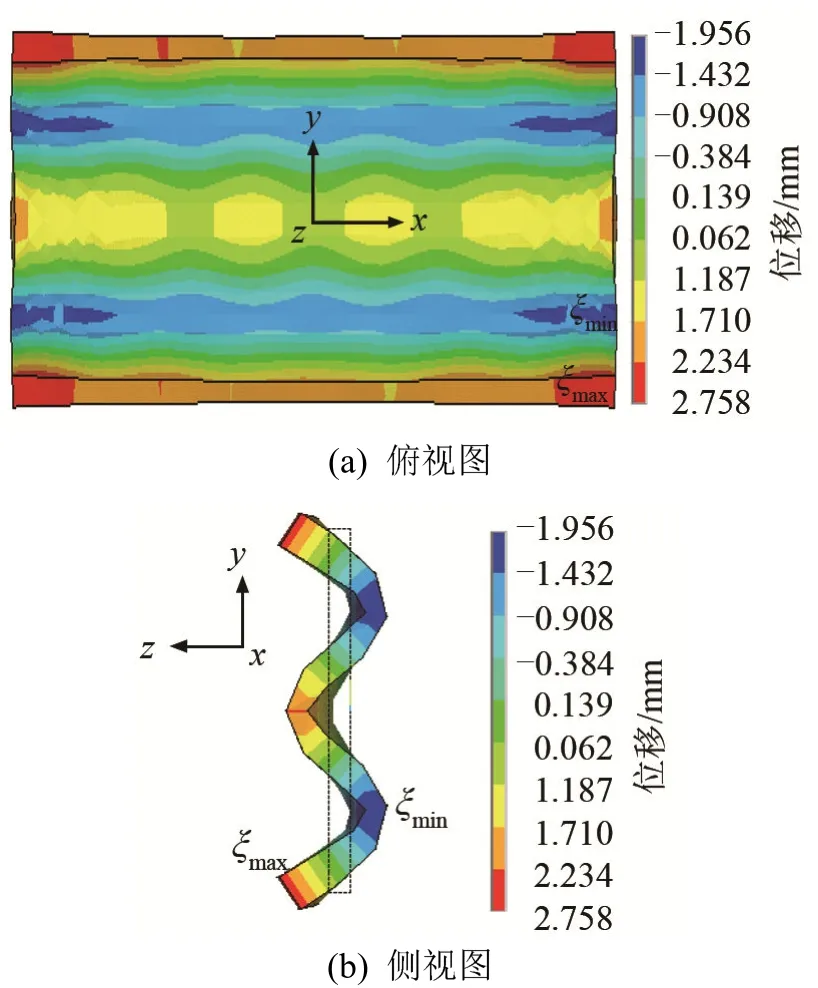
图3 矩形平板辐射体位移分布Fig.3 Displacement distribution of the single flat rectangular plate radiator

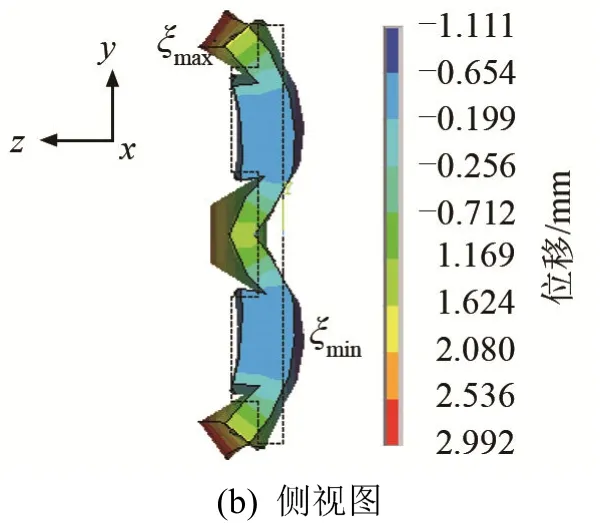
图4 矩形阶梯辐射体位移分布Fig.4 Displacement distribution of the stepped rectangular plate radiator
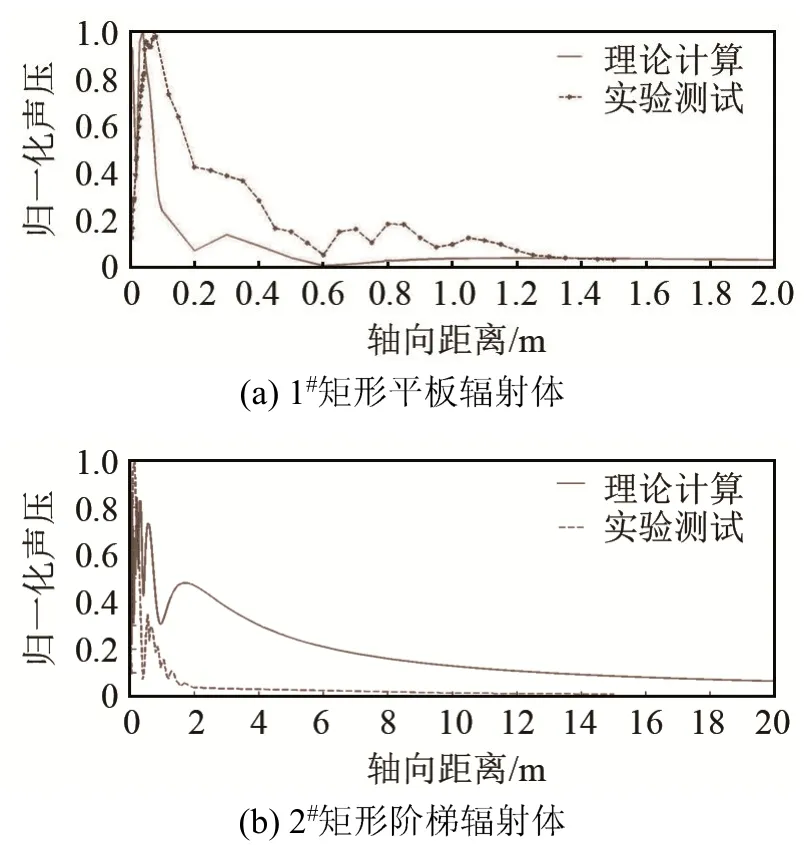
图5 矩形板辐射体轴向声压与距离的关系Fig.5 The relationships between axial pressure and axial distance for the 1# and 2# rectangular plate radiators
3 实验测试
实验中加工了算例中的1#和2#辐射体,实物如图6所示。实验测试装置包括声级测量分析仪、换能器、超声波发生器、数字功率计和麦克风(型号为uc-29,日本里音公司产,0.25 in (1 in=2.54 cm),频响范围为20 Hz~100 kHz)。实验装置如图7所示。超声波发生器施加电激励信号于换能器,换能器激励辐射体中心,麦克风正对辐射体的几何中心,其接收到的信号经过前置放大器放大后导入声级测量分析仪中,利用(LP表示声压级,pe表示待测声压的有效值,pref为参考声压,参考声压pref在空气中取为 2×10-5Pa)换算为空气中的声压。图8为辐射体轴向声压与输入功率的关系。

图6 1#矩形平板辐射体和2#矩形阶梯辐射体的实物照片Fig.6 The photographs of 1# flat rectangular plate radiator and 2# stepped rectangular plate radiator
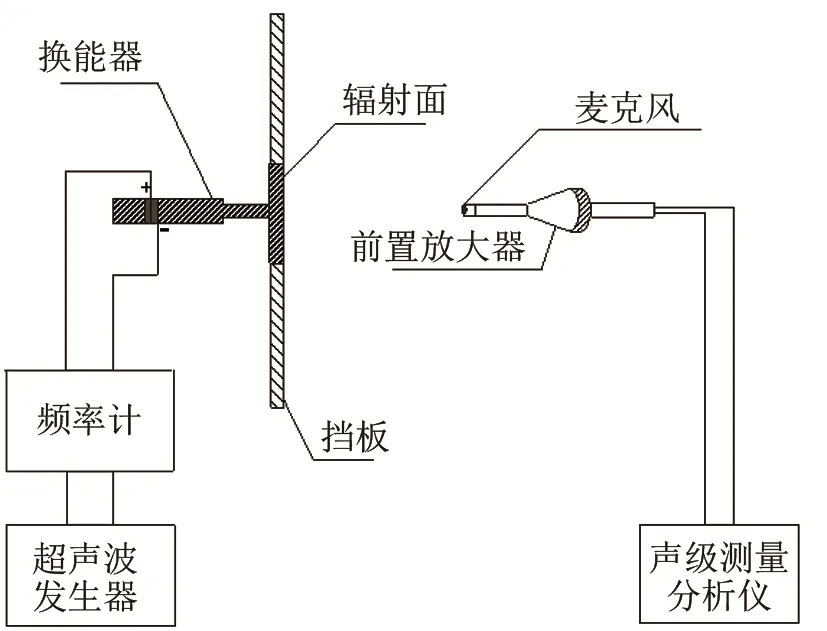
图7 实验装置图Fig.7 Experimental setup diagram
将测试得到的声压级换算成空气中声压后进行归一化处理,得到辐射体轴向距离与声压的关系,如图5(a)和5(b)中虚线所示。
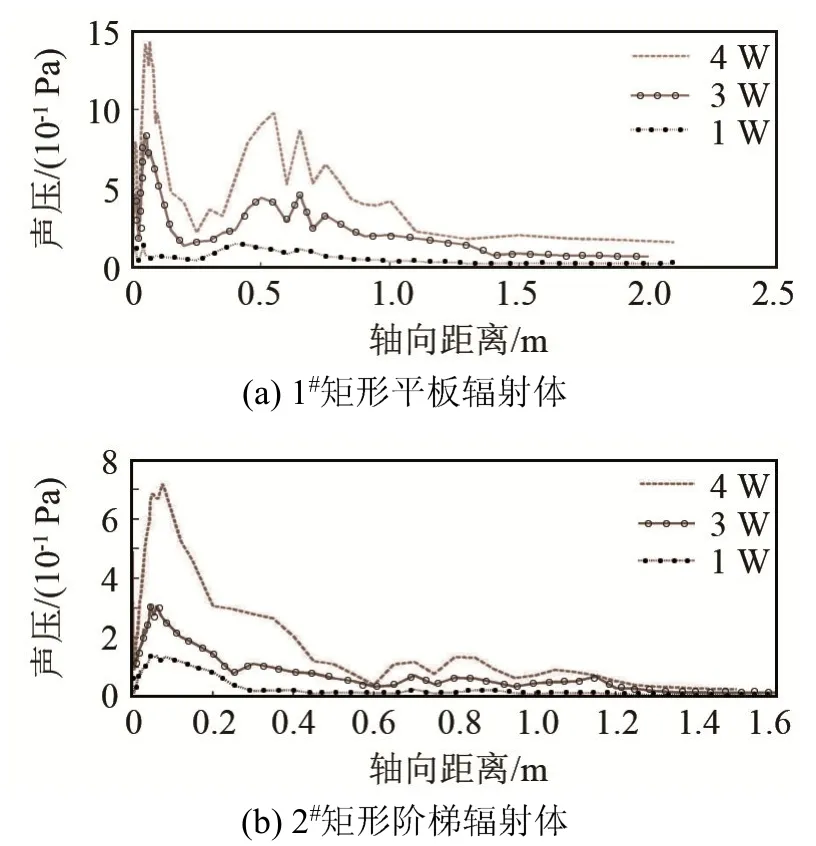
图8 不同输入功率下矩形平板辐射体和阶梯辐射体的轴向声压Fig.8 The axial pressures of flat rectangular plate radiator and stepped rectangular plate radiator under different input powers
4 分析与讨论
图5中实线所示为理论计算结果,虚线所示为实验测试结果,理论计算与实验测试结果均表明,2#矩形阶梯辐射体的近远场临界点距离其中心较远,在其近场区域声压起伏变化剧烈,极大值与极小值出现的频率较高,声压幅值差值较大。1#辐射体和 2#阶梯辐射体在其各自近声场中的理论计算与实验测试结果存在一些差异,主要表现在以下两个方面:首先,极大值与极小值出现的位置有偏移,其次,声压幅值变化的大小有差异。出现上述情况的可能原因是:(1) 在实验测试中移动麦克风时,麦克风距辐射体几何中心h的读数误差;(2) 理论计算时假设辐射体嵌置于无限大刚性障板中,而测试时辐射体实际嵌置于有限大障板中,从而造成的误差。但总体来说,计算与实验测试的近场和远场声压随轴向距离变化的趋势基本一致。
由图8可得,输入功率不同时,两个辐射体沿各自轴线方向的声压随距离的变化趋势基本一致,在各自近场区域,轴向声压随距离的增大有较大的起伏变化,极大值与极小值出现的频率较高;在远场区域,声压随距离的增加缓慢衰减,近场和远场声压随轴向距离变化的趋势基本一致。
5 结 论
(1) 本文推导了一种计算自由边界条件下弯曲振动矩形板辐射体近远场轴向声压的方法。以算例中的1#和2#矩形辐射体为例,分别计算了其轴向声压的变化规律,并进一步进行了测试,测试与计算结果基本一致。
(2) 在近场区域,1#和 2#矩形辐射体的声压均随轴向距离的增大有较大的起伏变化,在其各自的近场区域均多次出现极大值与极小值;在远场区域,两类辐射体的轴向声压均随距离的增加而缓慢衰减。
(3) 测试了声压与施加在激励换能器上的输入功率之间的关系。输入功率不同时,辐射体轴向声压随距离变化的趋势相同,进一步说明该方法是可行的。
