轮缘槽宽度对固定辙叉轮轨关系影响研究

2021-01-08赵卫华曹洋王启云康晶晶马彬斌

铁道科学与工程学报 2020年12期

赵卫华，曹洋，王启云，康晶晶，马彬斌

轮缘槽宽度对固定辙叉轮轨关系影响研究

赵卫华1，曹洋2，王启云1，康晶晶1，马彬斌1

(1. 福建工程学院地下工程福建省高校重点实验室，福建福州 350118；2. 福州大学土木工程学院，福建福州 350108)

为明确固定辙叉轮缘槽宽度对辙叉区轮轨关系的影响，基于轮轨接触理论和车辆—道岔耦合振动理论，提出以轮载过渡断面等轮轨接触几何参数为主要评价指标的轮缘槽宽度优化方法，分析轮缘槽宽度对固定辙叉区轮轨接触几何关系和轮轨动力相互作用的影响。研究结果表明：在轮载过渡区，合理减小轮缘槽宽度可增大实际轮载过渡断面心轨轨头宽度且降低等效锥度发生突变几率；辙叉轮缘槽宽度变化对轮轨动力相互作用影响不大，各动力学指标幅值变化极小，进一步验证了以轮轨接触几何参数为主要评价指标的轮缘槽优化方法的可靠性。

固定辙叉；道岔；轮缘槽；轮轨接触关系；轮轨动力相互作用

固定辙叉道岔因其结构组件较少、结构相对稳定等优点，广泛使用于我国货运重载线路与客运提速线路[1]。由于固定辙叉区翼轨和心轨相对位置固定，存在轨距线不连续区段，且沿辙叉走行方向各钢轨断面廓形和轨下刚度不规则变化，造成列车过岔时轮轨动力相互作用较区间线路更加剧烈[2−4]，辙叉区钢轨特别是翼轨和心轨轨头裂纹、剥离掉块、肥边、磨耗等各类病害[5]多发。国内外学者从结构设计参数优化[6−12]和轮轨动力相互作用模型[13−16]方面对固定辙叉开展过相关研究。其中，徐井芒等[6-7]分别从轮轨磨耗角度和轮载过渡段轮轨接触几何关系角度提出固定辙叉心轨关键断面廓形优化方法；王树国等[8]从理论计算、试验验证和动力仿真分析角度对固定辙叉查照间隔、护轨轮缘槽宽度和心轨顶面宽度进行了优化；Palsson[9]通过对翼轨和心轨关键断面廓形以及各断面降低值进行参数化，提出考虑车轮踏面廓形集的固定辙叉廓形优化方法；WAN等[10−12]基于固定辙叉轮轨动力相互作用的数值模拟和现场试验结果，对不同动力响应进行权重分析并结合多目标优化方法提出了固定辙叉心轨廓形优化方法。Wiest[13−14]对比分析目前广泛采用的道岔区轮轨动力相互作用的4种动力学模型，通过对一系列动力响应进行对比分析指出各模型的优缺点，并分析了列车荷载作用下心轨的变形和磨耗情况。既有文献包含了固定辙叉区轮轨相互作用的众多影响因素的研究，如翼轨加高值，心轨降低值，轮载过渡段长度，翼轨与心轨相对高差等参数，但对辙叉翼轨与心轨轮载过渡段轮缘槽宽度的研究却较少。列车通过固定辙叉时会引起轮轨剧烈振动，加速辙叉的损坏，轻则导致轮缘撞击心轨尖端，重则轮缘进入异侧轮缘槽，发生脱轨事故，因此开展辙叉轮缘槽宽度对轮轨关系影响的研究具有重要意义。本文基于轮轨接触关系理论和轮轨系统动力学理论，在明确固定辙叉轮载过渡机理的前提下，提出了以轮载过渡断面等轮轨接触几何参数为主要评价指标、动力学评价指标为辅的辙叉轮缘槽宽度优化方法，分析不同轮缘槽宽度情况下，磨耗型车轮踏面与辙叉轮载过渡段钢轨的接触几何关系和变化规律，以及轮轨动力特性的变化规律，进而寻求轮缘槽宽度与心轨翼轨廓形的合理匹配关系，为固定辙叉轮缘槽宽度优化设计提供指导。

1 固定辙叉轮轨接触几何关系

1.1 固定辙叉结构特点

固定辙叉道岔广泛使用于货运重载线路与客运提速线路，主要结构特点包括多钢轨参振、岔枕参振质量不同以及不规则钢轨截面特性。而不规则钢轨截面特性决定了列车过岔时轮轨接触点空间位置和数量的变化，从而导致轮轨接触关系复杂及固有的结构不平顺。因此，在道岔区轮轨接触关系及动力学研究中，采用实际的辙叉区轨头截面廓形是十分必要的。借助CAD绘图软件自动提取钢轨横截面廓形数据，然后利用三次样条插值函数拟合形成光滑曲线代表钢轨廓形。其他任意截面钢轨廓形可由两侧相邻的关键截面线性插值获得。如图1所示。

图1 固定辙叉任意截面廓形生成

1.2 轮轨接触几何关系评价指标

道岔区轮轨接触几何关系评价指标包括踏面等效锥度，轮对侧滚角，竖横向结构不平顺等接触几何关系参数。固定辙叉区轮轨接触几何参数确定与区间线路相同，采用迹线法和最小距离法[17]获得轮轨接触点位置并计算求得各项接触几何参数。

1.2.1 轮对侧滚角

轮对侧滚角是反映列车过岔时车体横向稳定性的指标，轮载转移越缓慢，轮对倾角越大，轮轨间动力作用越剧烈，便容易造成轨道结构损坏，存在较大的安全隐患。

1.2.2 踏面等效锥度

此参数反映了轮对滚动圆半径r和r的变化情况，以及车轮行驶过程中回复至名义滚动圆半径处的能力。依据区间线路车轮的实际滚动圆半径求解公式[13]可导出固定辙叉区踏面等效锥度与车轮滚动圆半径的关系：

式中：r0和r0分别为轮对没有发生横移时左右车轮的实际滚动圆半径；r和r分别为轮对发生横移时左右车轮的实际滚动圆半径；y为轮对横移量；λ为踏面等效锥度。

1.2.3 结构不平顺

由于翼轨、心轨截面宽度和纵断面高度不断变化，接触点位置沿辙叉走行方向不断改变，产生了轮轨接触点在横向及竖向的变化，称之为辙叉的“结构不平顺”，它是轮轨动力作用及轮对蛇形运动的激励源。根据列车过岔时产生的激扰作用方向，结构不平顺可分为横向和竖向不平顺。计算方法如图2所示。

图2 结构不平顺求解示意图

以轨距测量点为坐标原点，设无轮对横移时辙叉趾端轮轨接触点距轨距测量点的横向距离为0，竖向距离为0，该接触点称为理论接触点，则轮对在辙叉其他部位任意实际接触点在该坐标系中的位置可表示为(,)，所对应的辙叉横向不平顺Y和竖向不平顺Z如式(2)所示。需要说明的是，横向不平顺以实际接触点至坐标原点的横向距离较理论接触点远为正，竖向不平顺也是以实际接触点至坐标原点的竖向距离较理论接触点远为正；反之则为负。

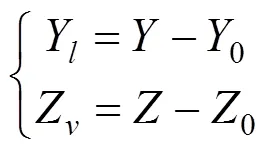
1.2.4 极限过渡断面与实际过渡断面

轮载在心轨和翼轨之间过渡时，基于2方面确定轮载过渡段边界条件，一方面，为了保证车轮踏面从翼轨过渡到心轨(逆向进岔)时，在心轨处不会被卡住或者脱轨，车轮踏面脱离翼轨时对应的心轨断面称为极限过渡断面，轮对横移量不同，对应的极限过渡断面不同；另一方面，为了防止心轨薄弱断面过早与车轮踏面接触，规范规定心轨顶宽20 mm断面以下部分不能承受列车荷载，即不能与车轮踏面接触，心轨顶宽20 mm断面称为最小承载断面。心轨最小承载断面和极限过渡断面确定的心轨可承载范围即为轮载合理过渡段，如图3阴影部分所示。该范围内任意断面均有可能成为轮载从翼轨完全转移到心轨时对应的心轨断面，称为实际过渡断面。由于最小承载断面由设计标准唯一确定，而心轨极限过渡断面和轮载实际过渡断面均会受到辙叉结构设计参数如翼轨加高值，心轨降低值，轨距，轮缘槽宽度等的变化以及轮对横移量的变化而改变，因此将其作为固定辙叉区轮轨接触关系评价指标之一。

图3 辙叉心轨轮载过渡段

2 车辆—道岔动力相互作用计算模型

车辆—道岔耦合振动模型可分为车辆子系统和道岔子系统及轮轨接触关系3部分。在充分考虑车辆与固定辙叉道岔结构型式、振动特性等因素基础上，通过对车辆系统和固定辙叉道岔系统进行合理简化，建立了车辆—固定辙叉耦合动力学模型，用于固定辙叉轮轨动力学评价指标的计算，如图4所示。其中车辆模型采用文献[18]建立的整车模型；考虑到列车进入固定辙叉区的轮轨动力响应会受到列车通过转辙器部分和连接部分时的振动传递效应的影响，同时为了考虑车辆长度和消除边界效应，实际建立模型为道岔整体模型，而非辙叉局部模型，模型中各部件的模拟参考文献[19]；车辆系统和道岔系统通过轮轨接触耦合，其中垂向耦合可以看做两个椭球状弹性体的接触，简化为非线性赫兹接触问题；横向耦合受多种因素制约，使列车产生不同程度的横向振动和蛇形运动，可采用非线性蠕滑理论进行模拟。

文中涉及相关参数选取依次为：列车速度取为160 km/h，车辆参数参考文献[18]附表3中提速客车相关参数；车轮踏面采用LM型。道岔类型选取60 kg/m钢轨12号固定辙叉式道岔，动力学基本参数参考文献[19]。

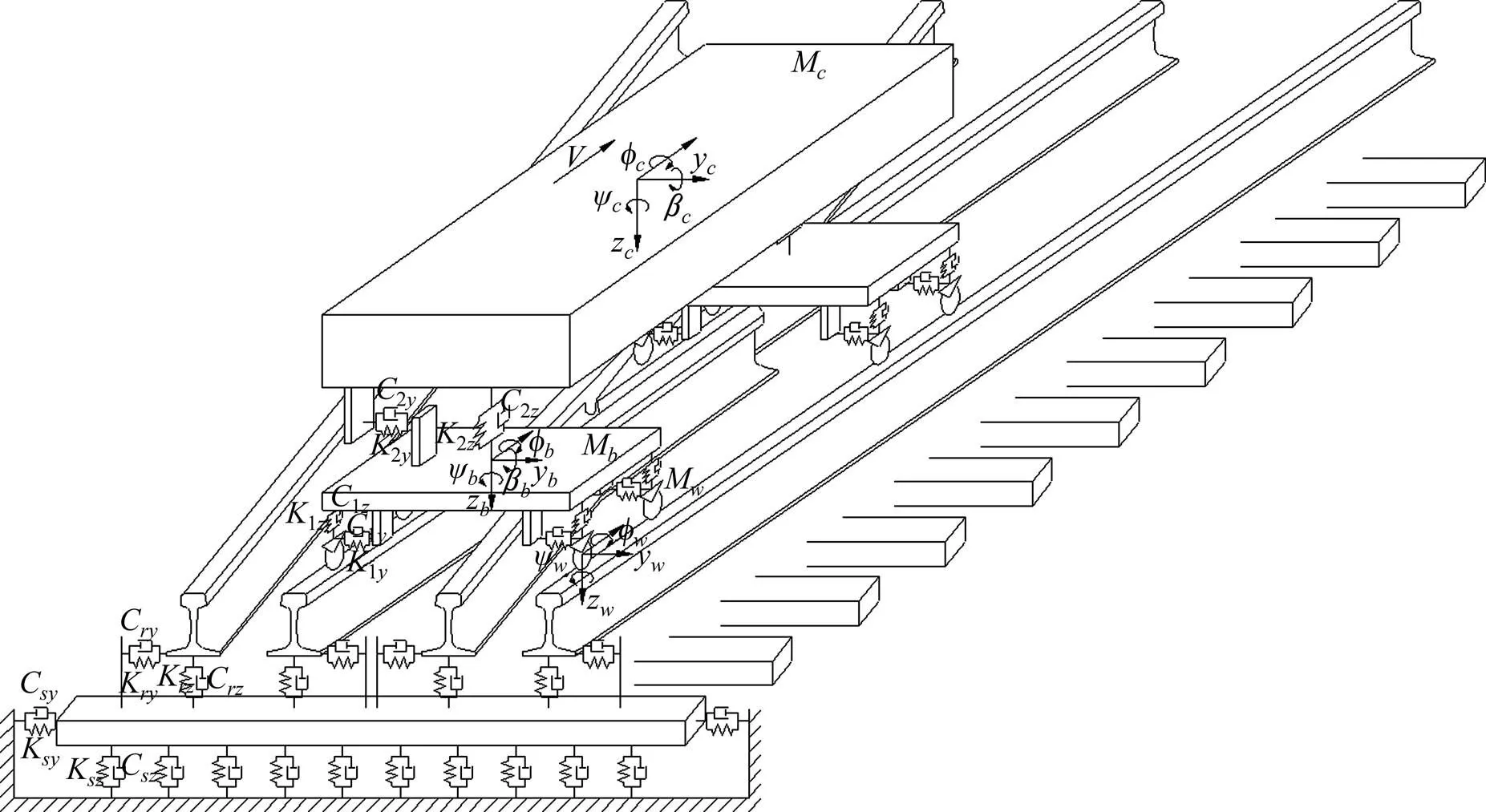
图4 车辆-道岔动力耦合模型

3 轮缘槽宽度对轮轨接触几何关系的影响

3.1 方案设置

固定辙叉结构各部位轮缘槽宽度影响轮轨游间以及轨距大小，进而影响轮轨接触几何关系。其中辙叉轮缘槽宽度是衡量心轨工作边与翼轨工作边距离的设计参数，如图5所示。轮缘槽宽度对轮载过渡段轮轨关系优化具有至关重要的作用。因此，本文通过调整辙叉区轮缘槽宽度，分析其对轮轨接触几何参数的影响，从而寻求辙叉区最佳轮缘槽宽度的设计方案。依据《道岔设计手册》[20]，辙叉轮缘槽宽度取值应不小于45 mm，因此4种设计方案依次取45，46，48和50 mm作为辙叉轮缘槽宽度。

图5 辙叉轮缘槽示意图

3.2 结果分析

轮对横移量和辙叉轮缘槽宽度均会影响极限过渡断面的大小，图6为不同轮对横移量下各方案极限过渡断面的比较，图7所示为各方案实际过渡断面与最不利工况(方案4)极限过渡断面的比较，其中轮对横移量以指向辙叉侧为正。

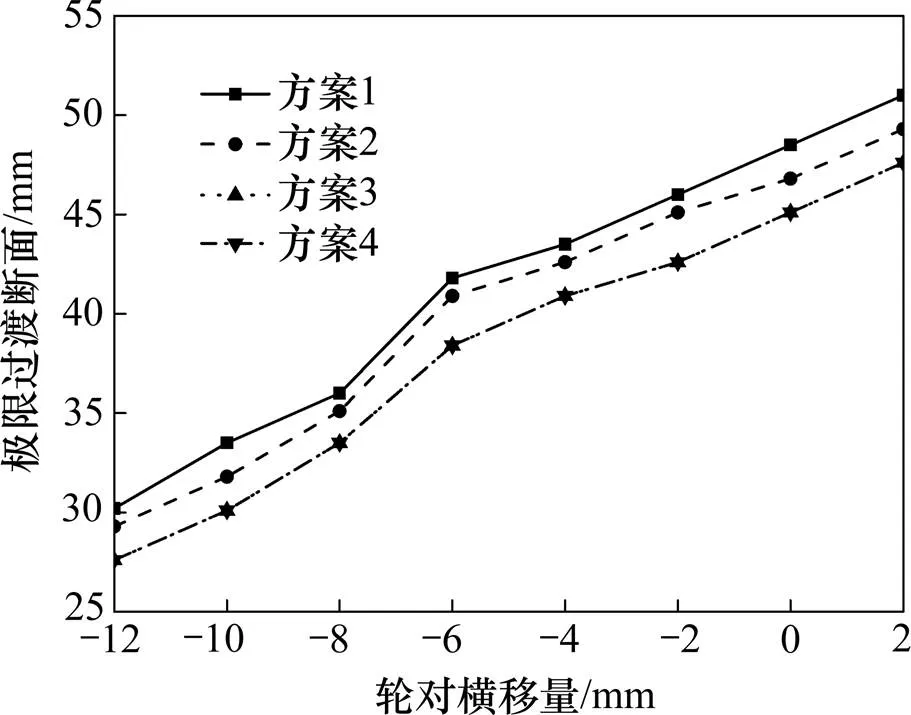
图6 各方案极限过渡断面

图7 各方案实际过渡断面与最不利极限过渡断面

图6可知，各方案极限过渡断面随轮对横移量的变化规律一致，随着轮对向辙叉方向横移量增加，极限过渡断面呈近似线性增大；同一横移量情况下，极限过渡断面随辙叉轮缘槽宽度增大而减小，这是由于轮缘槽宽度越大，车轮轮缘越早脱离翼轨而与心轨接触。方案3和4极限过渡断面基本一致，说明随着轮缘槽宽度增大，极限过渡断面宽度不再减小而是趋于稳定。各方案极限过渡断面与实际过渡断面对比发现，4种方案下实际过渡断面均小于方案4对应的最不利极限断面，如图7所示。各方案实际过渡断面均小于极限过渡断面，且均在心轨顶宽20～30 mm断面的范围内，说明列车通过各方案辙叉区时均不会出现脱轨或车轮被卡住的安全性问题。随着轮缘槽宽度的逐渐增大，实际过渡断面逐渐减小，表明轮载转移点向心轨理论尖端方向靠近，与实际运营情况相符，因此，在满足安全性要求的前提下，应尽量选取较小的轮缘槽宽度，以此增大实际轮载过渡断面轨顶宽度来减缓叉心钢轨磨耗，提高其使用寿命。

各方案的等效锥度、轮对侧滚角、结构竖向不平顺及横向不平顺的比较如图8～11所示。

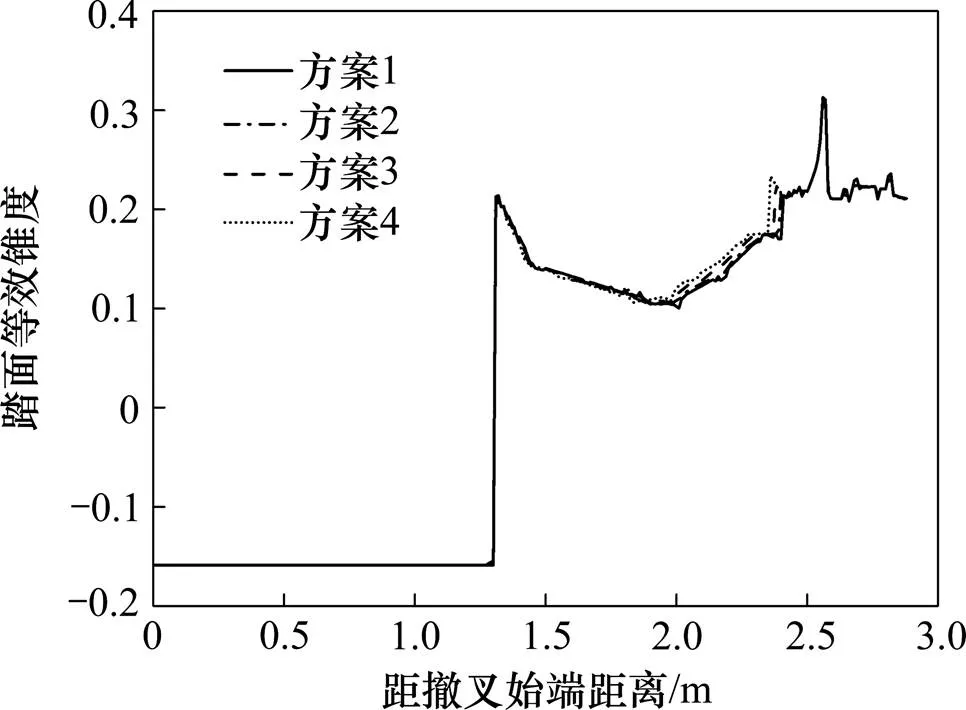
图8 踏面等效锥度

图9 轮对侧滚角

由图8可知踏面等效锥度在距辙叉始端1.3 m位置发生突变增大，主要因为此处为翼轨缓冲段始端，即翼轨开始偏离标准轨距线，造成辙叉侧轮轨接触点外移，实际滚动圆半径突然变小，结合踏面等效锥度的定义可知此处会出现阶跃。由图10和图11可知，从翼轨缓冲段始端到轮载过渡断面前，竖向不平顺和横向不平顺数值逐渐均匀增大，表明随着翼轨向外侧偏移，辙叉侧轮轨接触点逐渐向翼轨非工作边侧偏移；在轮载实际过渡断面范围内，轮轨接触点发生从翼轨向心轨的转移转变，由于不考虑两点接触及轮轨弹性变形，这里接触点的转移表现为突变，即在车轮运动至某一截面，接触点突然从翼轨转移至心轨，所以接触点在转移到心轨后，竖横向不平顺数值迅速减小。

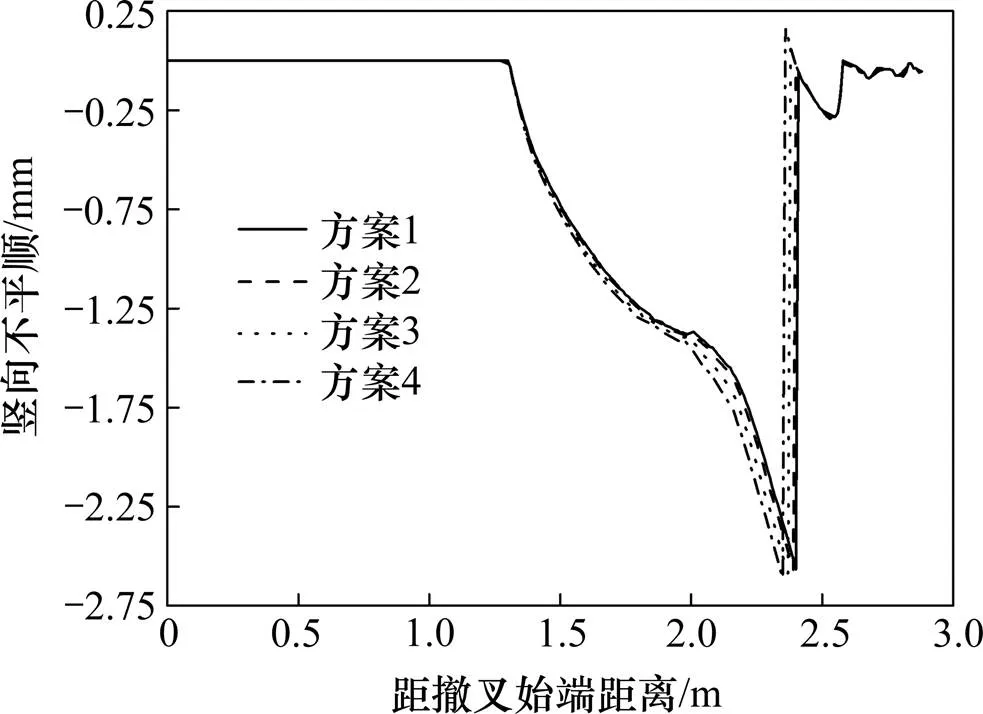
图10 竖向不平顺

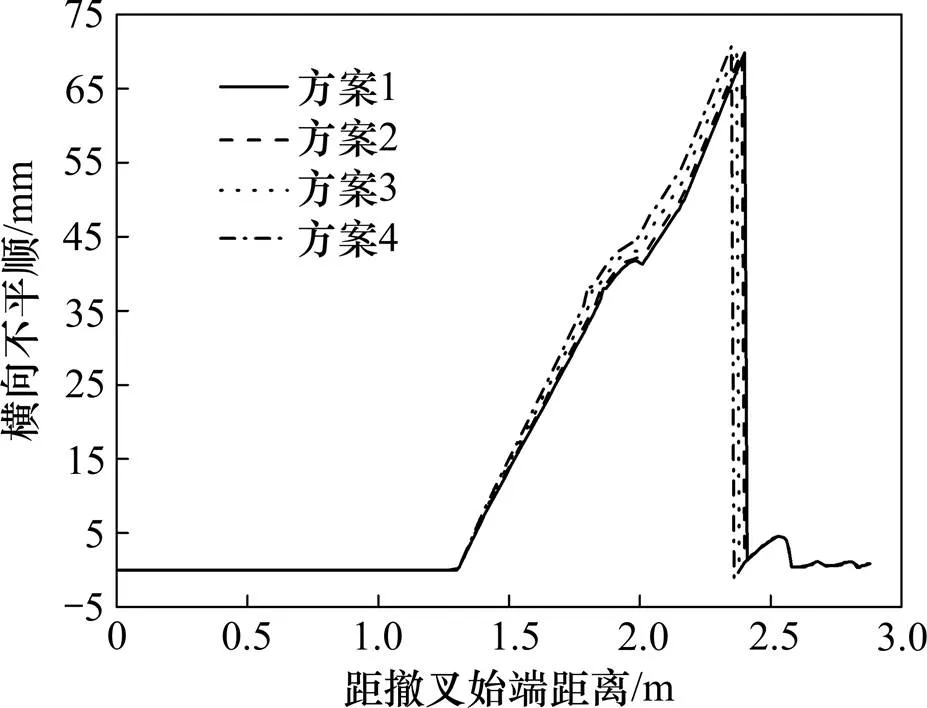
图11 横向不平顺

综合图8～11可知，随轮缘槽宽度的增加，等效锥度、轮对倾角、竖横向不平顺变化规律及大小相差很小，各指标最大值均逐渐增加，但增加幅度较小。因此，从轮轨接触几何关系的角度考虑，轮缘槽宽度减小可降低辙叉区竖向不平顺及横向不平顺的变化率及幅值，达到提高行车平稳性的目的。

此外，方案4中轮对横移量较大时实际过渡断面已接近心轨顶宽20 mm断面，充分考虑翼轨磨耗严重等最不利情况，实际过渡断面会接近或者小于最小承载断面，从而加速心轨薄弱断面伤损速率，因此针对辙叉轮载过渡段心轨顶宽20 mm断面处轮对不同横移量下接触几何参数变化规律进行分析，如图12和图13所示。需要说明的是，轮对在心轨40 mm断面处已经完成轮载过渡，车轮踏面完全与心轨接触，因此心轨顶宽40 mm断面处各方案下踏面等效锥度和轮对侧滚角随轮对横移量的变化规律和数值均相同，说明在轮载完全过渡到心轨上时，车轮在任意情况下都不会与翼轨接触，轮缘槽宽度变化并不会影响各接触参数变化规律。

图12 踏面等效锥度

图13 轮对侧滚角

由图12可知，随着轮对向辙叉侧横移量的增大，方案4中等效锥度最先发生突变，且量值最大。说明轮缘槽宽度增加使车轮踏面与心轨在轮对横移量较小时就发生接触，明显增大对心轨的磨耗，必然会缩短心轨使用寿命，因此应尽量减小轮缘槽宽度。图13表明轮缘槽宽度变化对轮对侧滚角影响不大，轮载过渡段轮缘槽宽度对列车过岔时的横向稳定性影响很小。

不同轮缘槽宽度下辙叉区各项轮轨接触几何关系评价指标的对比分析表明了轮缘槽宽度对轮载过渡段内的轮轨关系有重要影响，在满足道岔构造设计的前提下，应尽量选取较小的辙叉轮缘槽宽度来增大实际轮载过渡断面、提高心轨粗壮度减小磨耗，同时提高行车平稳性。

4 动力特性分析

轮缘槽宽度依次取45，46和48 mm设置3种设计方案，最前方轮对轮轨作用力、车体振动情况及行车安全性指标最大值如表1所示。

表1 各方案轮轨动力响应最大值

由表1可知，由于列车直向过岔，使车岔系统垂向作用较横向剧烈。各方案基本轨侧轮轨垂向力最大值均小于辙叉侧相应值，而轮轨横向力最大值均大于辙叉侧相应值；随着轮缘槽宽度增加，辙叉侧和基本轨侧轮轨垂横向力和轮轴垂向力的最大值均增大，但各方案各轮轨作用力指标数值变化幅度均小于3%且小于安全限值；各方案脱轨系数远小于限值0.8，轮重减载率小于限值0.8；随着轮缘槽宽度增加，脱轨系数和轮重减载率数值均增大，但增值极小；说明轮缘槽宽度改变对轮轨作用力变化和列车过岔安全性影响很小。

最前方轮对辙叉侧轮轨作用力时程曲线如图14和图15所示，列车过岔过程中车体加速度时程曲线如图16和图17所示。

由图14～15可知，2方案辙叉侧轮轨间作用力变化规律一致，在结构不平顺影响下，轮轨间作用力在轮载过渡范围出现极值。图16～17表明，3方案车体加速度变化规律一致，同样受到辙叉结构不平顺影响，在轮对过叉时车体振动较大且达到最大值；由于竖向结构不平顺影响较大，车体垂向加速度明显大于横向加速度；随着轮缘槽宽度的增大，车体垂横向加速度量值变化较微弱。

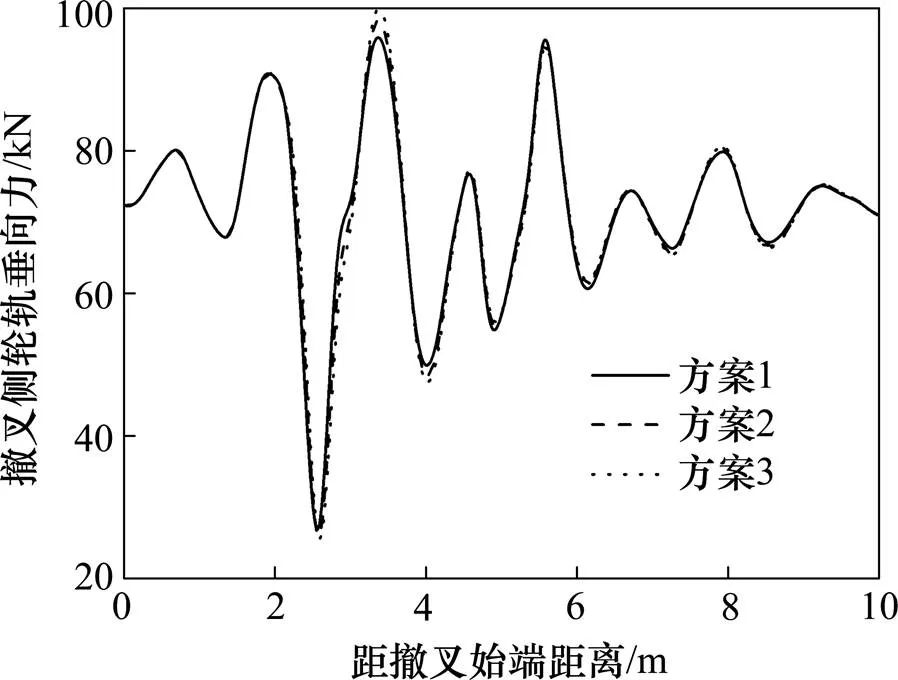
图14 轮轨垂向力

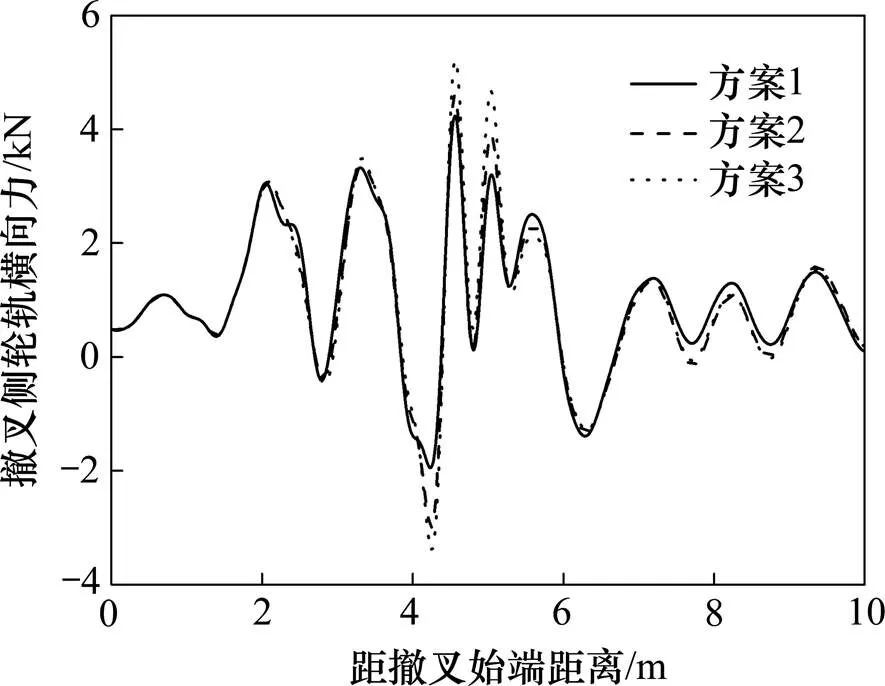
图15 轮轨横向力

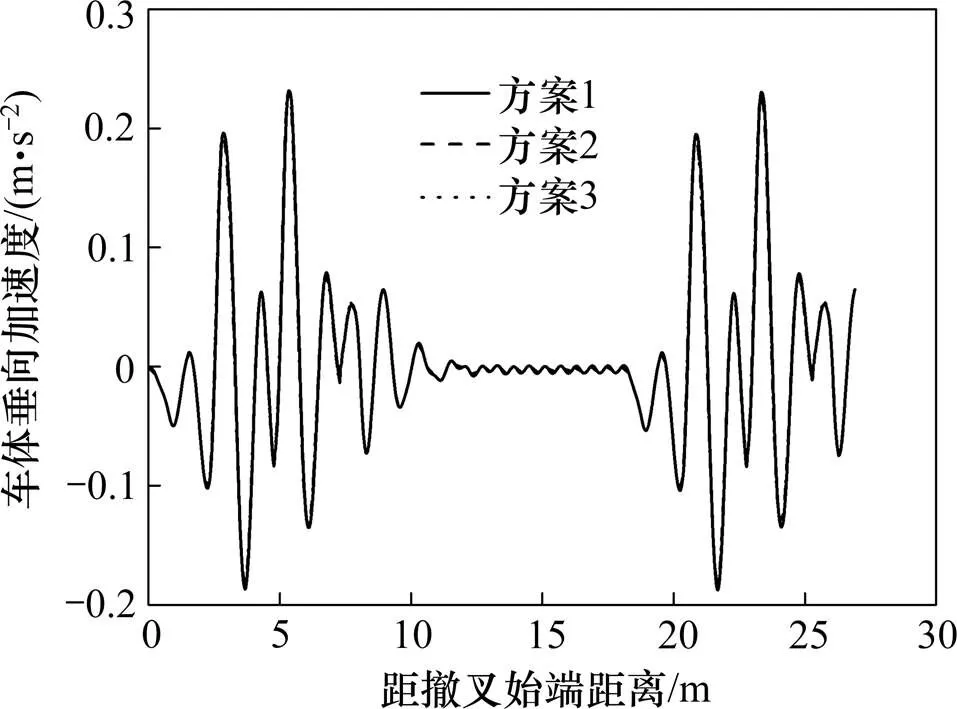
图16 车体垂向加速度

图17 车体横向加速度

综上所述，各方案各评价指标变化很小，说明轮缘槽宽度变化对轮载过渡段轮轨动力学评价指标影响不大，对固定辙叉轮缘槽宽度优化可采用轮轨接触几何参数指标进行评价。

5 结论

1) 通过比较轮对不同横移量下极限过渡断面与实际过渡断面轨顶宽度大小，确保设计方案满足列车运行安全性要求；轮缘槽宽度取值越大，实际过渡断面越靠近心轨尖端，因此建议在满足道岔构造设计要求的前提下，尽量采用较小的轮缘槽宽度来增大实际轮载过渡断面心轨轨顶宽度，从而减小心轨磨耗、提高辙叉使用寿命。

2) 在辙叉轮载过渡区，轮缘槽宽度增大，等效锥度发生突变的轮对横移量越小，即等效锥度发生突变的几率越大；说明车轮踏面与心轨在轮对横移量较小时就发生接触，明显增大了对心轨的磨耗。但是在轮载完全过渡到心轨后，轮缘槽宽度的变化并不改变各接触参数的变化规律。因此，相比其他固定辙叉结构设计参数，辙叉轮缘槽宽度只对轮载过渡段范围内的轮轨关系有影响。

3) 辙叉轮缘槽宽度变化对轮载过渡段轮轨动力相互作用影响较小，在进行固定辙叉关键结构设计参数优化时，对轮缘槽宽度的优化采用轮轨接触几何参数评价指标即可，动力学响应可作为辅助评价指标或者不做动力学评价。

[1] 易思蓉. 铁道工程[M]. 3版.北京: 中国铁道出版社, 2015. YI Sirong. Railway engineering[M]. 3rd ed. Beijing: China Railway Press, 2015.

[2] WANG Ping, XU Jingmang, XIE Kaize, et al. Numerical simulation of rail profiles evolution in the switch panel of a railway turnout[J]. Wear, 2016(366−367): 105−115.

[3] XIN L, Markine V L, Shevtsov I Y. Numerical procedure for fatigue life prediction for railway turnout crossings using explicit element approach[J]. Wear, 2016(366−367): 167−179.

[4] WAN Chang, Markine V L, Shevtsov I Y. Optimisation of the elastic track properties of turnout crossings[J]. Proc Inst Mech Eng Part F: J Rail Rapid Transit, 2016, 230(2): 360−373.

[5] 于淼, 张军, 鹿广清, 等. 重载货车作用下固定辙叉心轨磨耗分析[J]. 铁道学报, 2014, 36(7): 30−35. YU Miao, ZHANG Jun, LU Guangqing, et al. Analysis on wear of unmovable frog nose rail under the action of heavy-haul freight car[J]. Journal of the China Railway Society, 2014, 36(7): 30−35.

[6] 徐井芒, 王平. 基于轮轨廓型的固定辙叉优化设计方法[J]. 中国铁道科学, 2014, 35(2): 1−6. XU Jingmang, WANG Ping. Optimization design method for rigid frog based on wheel/rail profile type[J]. China Railway Science, 2014, 35(2): 1−6.

[7] 曹洋, 王平. 固定辙叉心轨轨顶降低值优化设计方法研究[J]. 西南交通大学学报, 2015, 50(6): 1067−1073. CAO Yang, WANG Ping. Optimization of nose depth for rigid frog[J]. Journal of Southwest Jiaotong University, 2015, 50(6): 1067−1073.

[8] 王树国, 葛晶, 司道林, 等. 固定辙叉查照间隔及心轨加宽研究[J]. 中国铁道科学, 2014, 35(1): 7−12. WANG Shuguo, GE Jing, SI Daolin, et al. Study on guard check gauge of fixed frog and design on widening nose rail[J]. China Railway Science, 2014, 35(1): 7−12.

[9] Palsson B A. Optimization of railway crossing geometry considering a representative set of wheel profiles[J]. Vehicle System Dynamics, 2015, 53(2): 274−301.

[10] WAN C, Markine V L, Shevtsov I Y. Improvement of vehicle-turnout interaction by optimizing the shape of crossing nose[J] Vehicle System Dynamics, 2014, 52(11): 1517−1540.

[11] WAN C, Markine V L, Shevtsov I Y. Analysis of train/turnout vertical interaction using a fast numerical model and validation of that model[J]. Pro IMechE Part F: J Rail and Rapid Transti, 2014, 228(7): 730−743.

[12] WAN C, Markine V L, Dollevoet R. Robust optimisation of railway crossing geometry[J]. Vehicle System Dynamics, 2016, 54(5): 617−637.

[13] Wiest M, Kassa E, Daves W, et al. Assessment of methods for calculating contact pressure in wheel- rail/switch contact[J] Wear, 2008, 265: 1439−1445.

[14] Wiest M, Daves W, Fischer F D, et al. Deformation and damage of a crossing nose due to wheel passages[J]. Wear, 2008(265): 1431−1438.

[15] Skrypnyk R, Nielsen J C O. Magnus E, et al. Metamodellng of wheel-rail normal contact in railway crossings with elasto-plastic material behaviour[J]. Engineering with Computers, 2019, 35(1): 139−155.

[16] SUN Y Q, Cole C, Boyd P. A numerical method using VAMPIRE modelling for prediction of turnout curve wheel-rail wear[J]. Wear, 2011(271): 482−491.

[17] 任尊松. 车辆动力学基础[M]. 北京: 中国铁道出版社, 2009. REN Zunsong. Vehicle dynamics basics[M]. Beijing: China Railway Press, 2009.

[18] 翟婉明. 车辆−轨道耦合动力学[M]. 3版. 北京: 科学出版社, 2007: 12−87, 392−396. ZHAI Wanming. Vehicle-track coupling dynamics[M]. 3rd ed. Beijing: Science Press, 2007: 12−87, 392−396.

[19] 刘学毅, 王平. 车辆−轨道−路基系统动力学[M]. 成都: 西南交通大学出版社, 2010: 127−178. LIU Xueyi, WANG Ping. Vehicle-track-subgrade system dynamics[M]. Chengdu: Southwest Jiaotong University Press, 2010: 127−178.

[20] 铁道部第三设计院. 道岔设计手册[M]. 北京: 人民铁道出版社, 1975: 413−503. Railway Ministry Third Design Department. Turnout design manual[M]. Beijing: People’s Railway Press, 1975: 413−503.

Study on influences of the flangeway width on the wheel/rail contact relationship in the fixed nose crossing

ZHAO Weihua1, CAO Yang2, WANG Qiyun1, KANG Jingjing1, MA Binbin1

(1. Key Laboratory of Underground Engineering of Fujian Province, Fujian University of Technology, Fuzhou 350118, China;2. College of Civil Engineering, Fuzhou University, Fuzhou 350108, China)

Based on wheel/rail contact theory and vehicle/turnout dynamic coupling theory, an optimization method was proposed to specify the influences of the flangeway width on the wheel/rail geometry contact relationship in the fixed nose crossing. This method employed wheel/rail geometry contact parameters as primary evaluation indexes to optimize the flangeway width. The influences of the flangeway width between the wing rail and the nose rail on the wheel-rail contact relationship and the wheel-rail dynamic interaction were analyzed based this method. The result shows that the flangeway width should be minimized to a reasonable magnitude in the wheel-load transition zone to decrease the probability of the sudden change of the equivalent conicity and thicken the practical wheel-load transition cross section and finally undermine the wheel-rail wear. The flangeway width has little influence on the wheel/rail dynamic interaction as the amplitude of all dynamic indicators in all schemes rarely change, which further validates the reliability of the optimization method which presents the wheel/rail geometry contact parameters as main evaluation indicators.

fixed nose crossing; turnout; the flangeway width; wheel/rail contact relationship; wheel/rail dynamic interaction