交变气动载荷作用下高速列车风机底板连接铆钉疲劳特性研究
2021-01-08付少青刘凯熊伟周伟
付少青,刘凯,熊伟,周伟, 3
交变气动载荷作用下高速列车风机底板连接铆钉疲劳特性研究
付少青1, 2,刘凯1, 2,熊伟1, 2,周伟1, 2, 3
(1. 中南大学 交通运输工程学院,湖南 长沙 410075;2. 轨道交通安全教育部重点实验室,湖南 长沙 410075;3. 轨道交通安全关键技术国际合作联合实验室,湖南 长沙 410075)
针对复杂服役环境交变气动载荷下高速列车底板-铆钉结构的疲劳损伤问题,提出基于服役气动载荷-铆钉结构应力分布的疲劳载荷谱编制及损伤评估方法。首先,建立列车底板/铆钉/梁板有限元模型,分析不同方向气动载荷下底板弯曲效应对铆钉结构强度的影响机理,获取气动载荷-铆钉应力的非线性传递因子;然后在列车底板布置气动差压测点捕捉底板服役气动载荷谱;最后,结合服役气动载荷谱和非线性传递因子编制铆钉结构的动应力载荷谱,基于雨流计数和Miners累积损伤准则建立铆钉结构二维八级载荷谱,并采用第四强度理论应力准则进行疲劳损伤评估。研究结果表明:在交变载荷下,高速动车组达到服役寿命960万km时,铆钉结构2个危险点在3个分区气动载荷及平均气动载荷作用下的疲劳总损伤分别为0.64,0.53,0.56,0.51和0.19,0.52,0.36,0.13。疲劳总损伤达到1.0,即认为铆钉结构气动致疲劳失效,由计算结果可知,高速动车组服役寿命内,铆钉结构能够满足使用要求。
高速列车;气动载荷;铆钉结构;载荷谱;疲劳损伤评估
在工程连接件应用中,铆接连接件以其良好的机械性能、连接可靠、质量轻、低成本、较强的环境适用性等特点而广泛应用于航空航天、机械、汽车及船舶等领域[1]。在高铁领域,我国高速列车的设备舱底板也广泛采用了铆接。近年来随着列车运行速度的不断提高,显著增加的空气动力学问题,列车所面临的力学环境变得更加复杂[2],因此高速动车组的服役安全性能也逐渐受到国内外学者的研究和关注。设备舱底板铆钉结构由于长期处在交变载荷的恶劣环境下工作,特别是开行在武广、郑西等存在大量隧道和隧道群的高速动车组[3],列车风机底板要受到较剧烈的气动载荷和冲击振动载荷的共同作用,而设备舱风机安装底板的高应力主要是由气动载荷引起的[4],因此研究气动载荷对铆钉疲劳的影响尤为必要。本文为研究交变气动载荷对铆疲劳脱落的影响,从载荷角度分析高速动车组在设计服役寿命960万km内,铆钉是否可以正常使用,而对铆钉疲劳损伤进行了预测。针对铆钉连接疲劳失效现象,国内外学者从不同角度出发,对铆接的疲劳寿命研究取得了一定成果。然而由于影响结构疲劳的因素过多、疲劳破坏没有先期预兆,研究困难较大,主要通过试验和仿真来分析铆钉产生疲劳的主要因素及对比其他连接方式来研究铆钉铆接的疲劳性能[5]。李风等[6]试验研究了在不同环境下的铆接疲劳强度曲线,并对铆钉搭接头疲劳寿命表达式进行了推导。Urban[7]对机身铆接结构进行了疲劳试验。Blanchot等[8]对铆钉进行有限元模拟,分析了铆钉结构应力分布等。Szymczyk等[9]对铆钉接头的位移和应力进行了分析,提出了预测铆钉连接件疲劳寿命的方法。目前针对铆钉疲劳的研究多局限于静强度连接结构的疲劳分析,对交变气动载荷因素对铆钉结构疲劳寿命的影响尚未有全面的研究,也缺乏全面的数据,本文主要考虑交变气动载荷作用下列车底板铆钉结构的疲劳问题。论文通过仿真方法得到气动载荷−铆钉应力的非线性传递因子,然后基于高速列车服役运行条件下的真实交变气动载荷谱作为依据,并根据服役载荷谱和非线性传递因子编制铆钉结构的动应力载荷谱,基于雨流计数和Miners累积损伤准则建立铆钉结构的二维八级载荷谱,最后采用第四强度理论应力(VON MISES)准则对列车铆钉的疲劳损伤及寿命进行评估,为后续连接件更换和维护提供理论 依据。
1 仿真计算模型
1.1 几何模型及材料参数
模型由底板,梁板以及用于连接底板和梁板的铆钉组成。其中梁板(底架横梁)是车体的一部分,底板通过铆钉铆接在梁板上。模型实际位于CRH380高速列车设备舱主风机安装底板上,底板作为设备舱的一部分,承受着来自设备舱上部的交变气动载荷作用。该模型底板长1 018 mm,宽363 mm,厚1.5 mm,梁板厚度5 mm,沿底板长度方向两侧各3个铆钉孔,用于安装铆钉,孔径5.5 mm,铆钉直径4.8 mm,模型尺寸位置如图2所示。同时,在不影响计算结果的前提下,为了便于网格划分,本模型删除底板上的细小圆孔及倒角。模型几何尺寸和实物图如图1(a)~1(b)所示。
安装底板,梁板以及铆钉,其各部分的材料参数如表1所示。

单位:mm

表1 模型各部分材料参数
1.2 网格划分
本模型利用ABAQUS软件,采用三维八节点C3D8R实体单元并采用缩减积分计算[10],这种类型的单元可以使计算结果更容易收敛。为保证结果的准确性,整体结构采用六面体进行网格划分,网格数量对铆钉连接处应力有影响,因此对重点关注的铆钉与底板和梁板的接触区域进行网格加密处理,因为此处可能会产生较大变形或应力集中,其他区域网格较为稀疏,从而建立起结构有限元模型。有限元模型共产生C3D8R实体单元86 580个, 节点112 103个,网格数量满足工程要求。底板−铆钉−梁板有限元模型如图2所示。
1.3 载荷、约束与接触
实验所得铆钉的拉伸极限强度为1 kN, 即钉芯的拉断力为1 kN,依据力的相互作用原理,得出拉铆钉的预紧力:r=1 kN。气动载荷由武广线上CRH380AL列车服役条件下的交变气动载荷获得,在底板沿车长方向的前、中及尾部位置布置差压传感器测点3个,如图3所示。
3个测点的气动载荷时程曲线如图4所示。

图2 底板−铆钉−梁板有限元模型

图3 风机底板结构气动载荷测点布置(沿车长方向)
根据图4时程曲线可知,气动载荷在−450 Pa至450 Pa之间,因此在底板整个面上施加从上往下的梯度均布载荷压力,大小450,350,…,50和从下往上的均布载荷−450,−350,…,−50,单位均为Pa。
约束:梁板作为车体的一部分,其在,,3个方向的位移是受到约束的,故约束平移自由度PINNED:1=2=3。

图4 测点气动载荷时程曲线
接触问题在工程中是一种高度的非线性行 为[11],该实体模型,考虑到了接触。在abquas 中铆钉分别与梁板和底板的接触1和3,梁板与底板之间接触2,底板与铆钉体接触4以及铆钉体与梁板之间的接触5均设置了接触,摩擦因数0.17,该模型共定义接触30对。接触如图5示。

图5 接触设置位置示意图
2 气动载荷−结构应力解算
2.1 结构应力分布
当在底板施加不同方向的气动载荷时,MISES最大应力为A与B 2点。下面就在不同方向施加气动载荷时铆钉MISES最大值点应力变化规律进行分析。
在1 000 N预紧力下,自上而下分别施加450 Pa和50 Pa气动压力时A点应力云图如图6。
在1 000 N预紧力下,自下而上分别施加−450 Pa和−50 Pa气动压力时B点应力云图如图7所示。

(a) 450 Pa铆钉应力云图;(b) 50 Pa铆钉应力云图

(a) 450 Pa铆钉应力云图;(b) 50 Pa铆钉应力云图
在1 000 N预紧力下,无气动载荷施加时应力云图如图8所示。
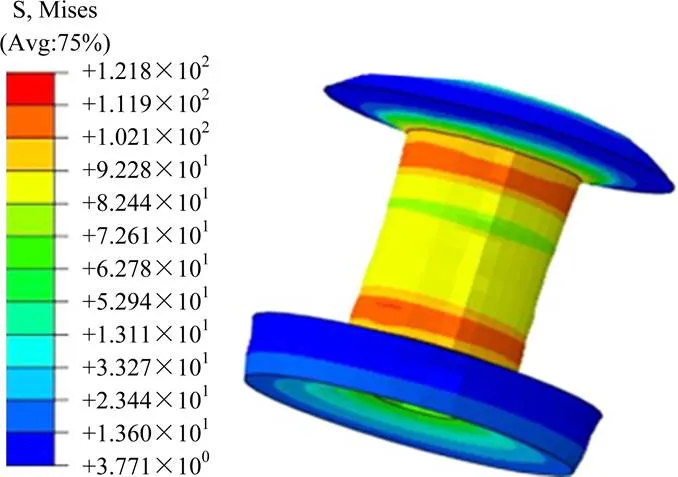
图8 气动载荷为0,预紧力1 000 N时应力云图
通过静力学分析得出其最大应力分布理论上存在于铆钉和被连接件的接触部位以及杆部分。从仿真结果来看,铆钉最大应力出现在了铆钉头和被连接件的接触部位,与理论分析相一致。从应力云图可以看出,气动载荷变化对铆钉应力的影响较预紧力相对较小。
2.2 应力传递因子计算
模型计算了铆钉在预紧力下,对底板施加从上向下及从下往上的梯度气动压力值,得到铆钉结构的应力大小及分布规律,并得到MISES应力各分量与气动载荷之间的数学关系式。
根据仿真得到A点MISES应力分量与气动载荷间的关系曲线如图9(a)~9(f)所示。
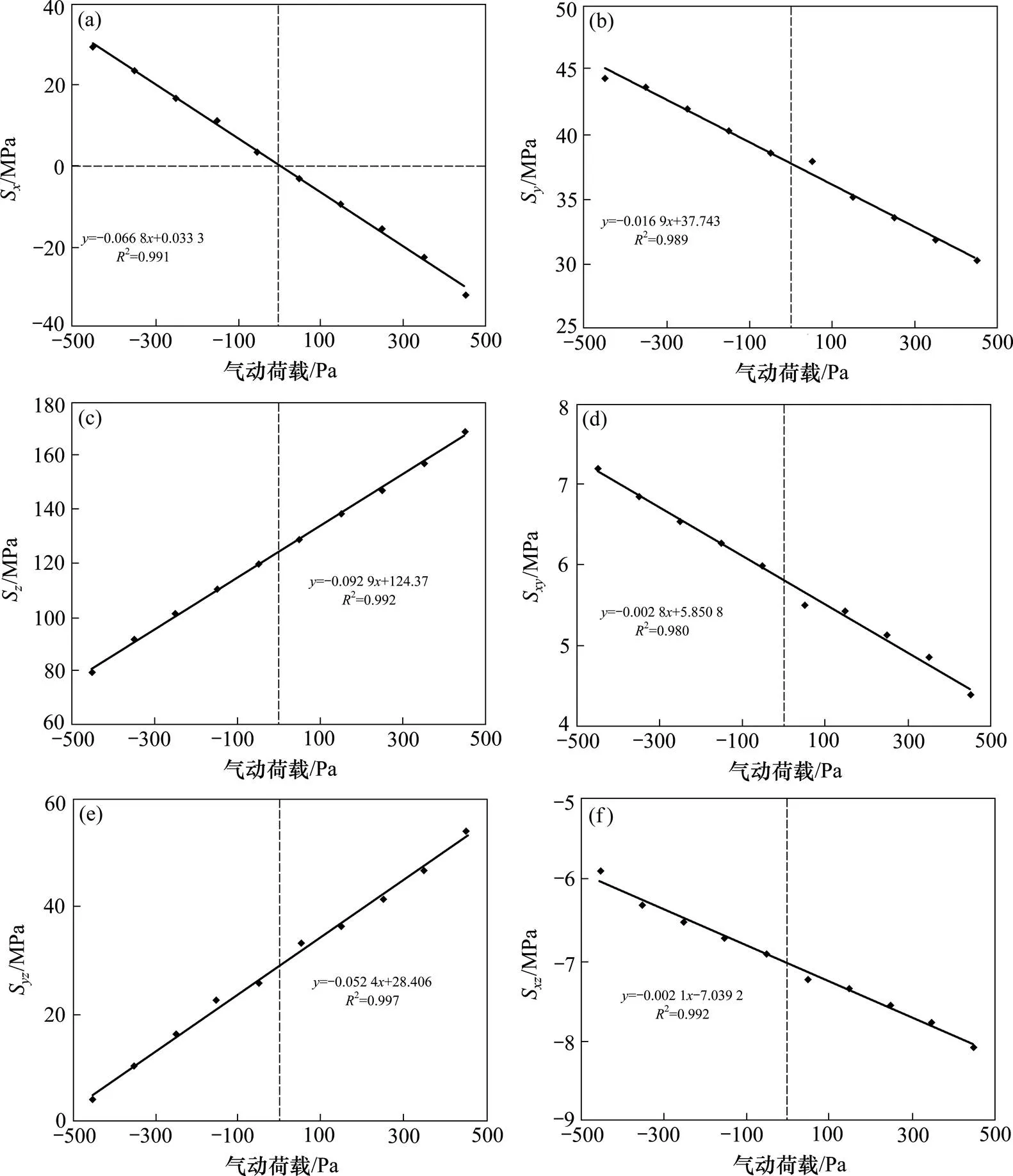
(a) Sx与气动载荷曲线拟合式;(b) Sy与气动载荷曲线拟合式;(c) Sz与气动载荷曲线拟合式;(d) Sxy与气动载荷曲线拟合式;(e) Syz与气动载荷曲线拟合式;(f)Sxz与气动载荷曲线拟合式
根据结构仿真结果绘制B点六应力分量与气动载荷的关系曲线如图10(a)~10(f)所示。
因此,根据图9和图10可以得到钉结构MISES各应力分量与气动载荷之间的一一映射关系−即可得应力传递因子。
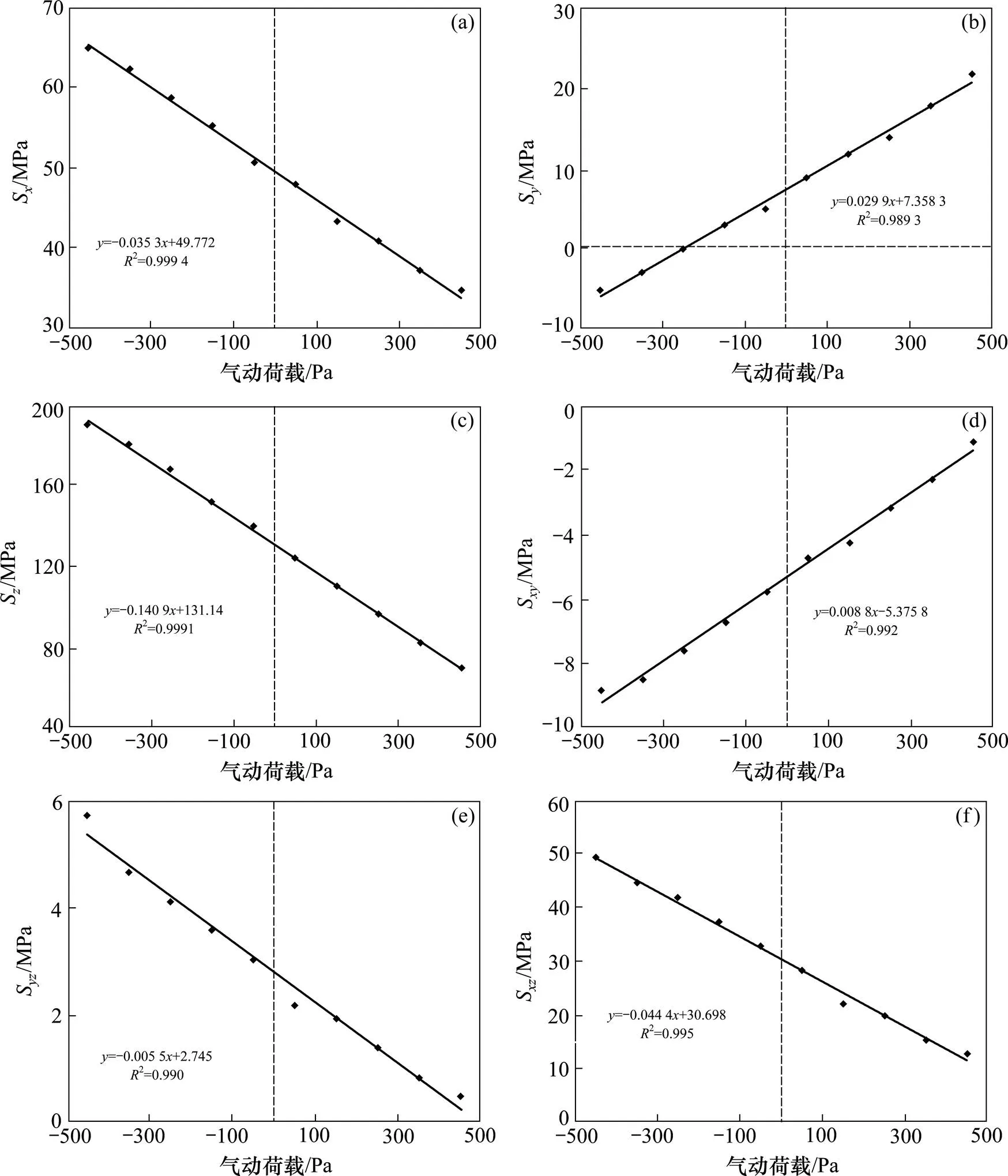
(a) Sx与气动载荷曲线拟合式;(b) Sy与气动载荷曲线拟合式;(c) Sz与气动载荷曲线拟合式;(d) Sxy与气动载荷曲线拟合式;(e) Syz与气动载荷曲线拟合式;(f) Sxz与气动载荷曲线拟合式
3 铆钉结构疲劳分析及寿命预测
3.1 铆钉疲劳载荷谱的编制
3.1.1 风载时程−应力时程转换
要对铆钉结构进行疲劳评估,应首先将得到的气动载荷谱转换为应力载荷谱。本文采用第4强度理论应力大小EQV进行分析。第4强度理论应力大小EQV公式如式(1)所示
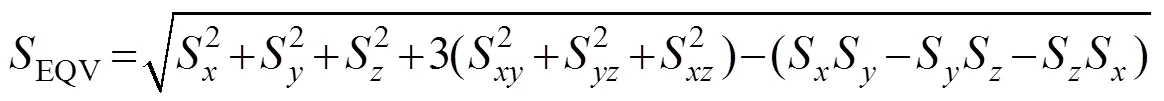
式中:S,S,S,S,S和S为仿真六应力分量。
根据仿真得到的六应力分量,代入式(1)便可得到在气动载荷下不同时刻EQV的大小。铆钉A点和B点第4强度理论应力分布如图11(a)和11(b)所示(以3测点平均载荷为例)。
3.1.2 八级载荷谱编制
本文采用雨流计数法对载荷均幅值进行统计后,得到应力时间历程中各次载荷循环中应力均幅值。随后通过编制载荷谱对载荷均幅值进行简化,从而得到能够表征铆钉结构真实气动载荷作用下的应力状况以及可用于疲劳损伤计算的程序谱[12]。编制的疲劳载荷谱应能真实模拟列车底板在实际运行过程中所受的交变载荷和发现疲劳薄弱位置并能够准确预测铆钉结构的疲劳寿命[13],而八级载荷谱可以满足工程精度要求,故采用二维八级载荷谱计算。
铆钉危险点A在3个分区及其平均二维应力均幅值载荷谱三维柱状云图如图12所示。

(a) A点第4强度理论应力分布;(b) B点第4强度理论应力分布
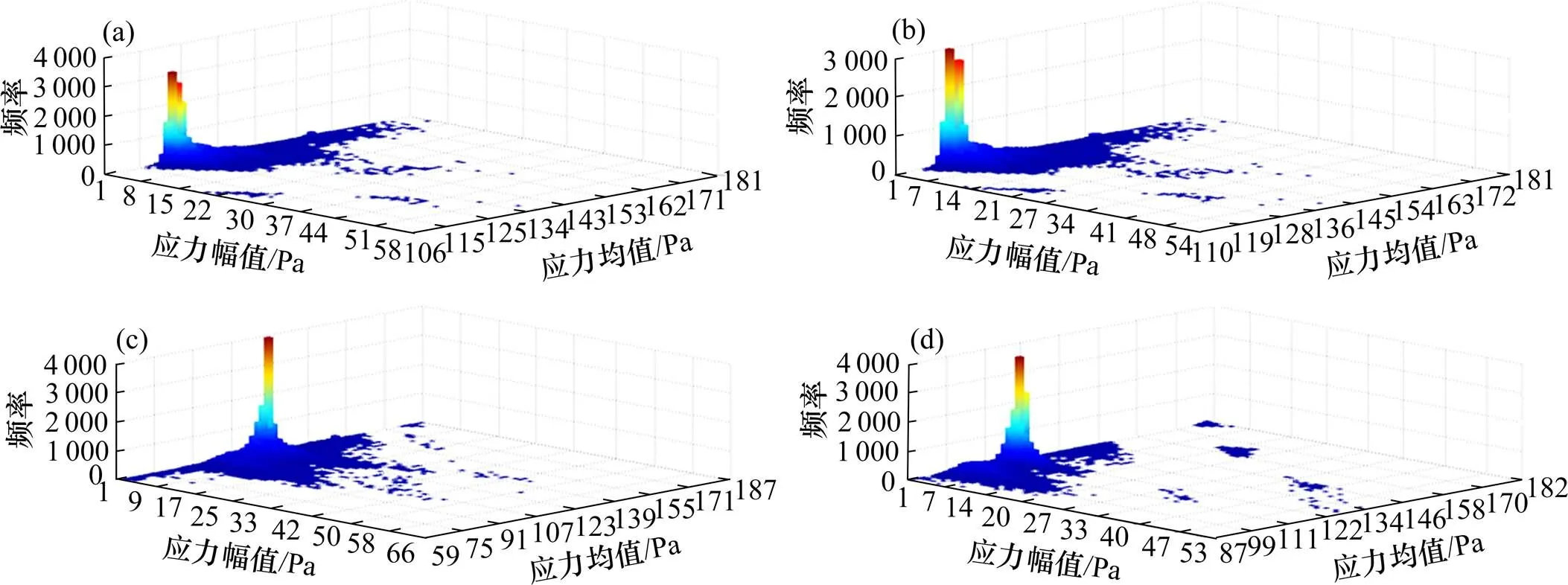
(a) 3点平均值;(b) 测点1;(c) 测点2;(d) 测点3
危险点A在底板分区3个测点应力均值分布有所不同,测点1、测点2和测点3应力均值分别主要分布在123~141 MPa,99~131 MPa和105~140 MPa。3个测点波动中心也各有差异,分别依次在114~176 MPa之间、67~179 MPa之间和93~176 MPa之间。
铆钉危险点B在3个分区及其平均二维应力均幅值载荷谱三维柱状云图如图13所示。
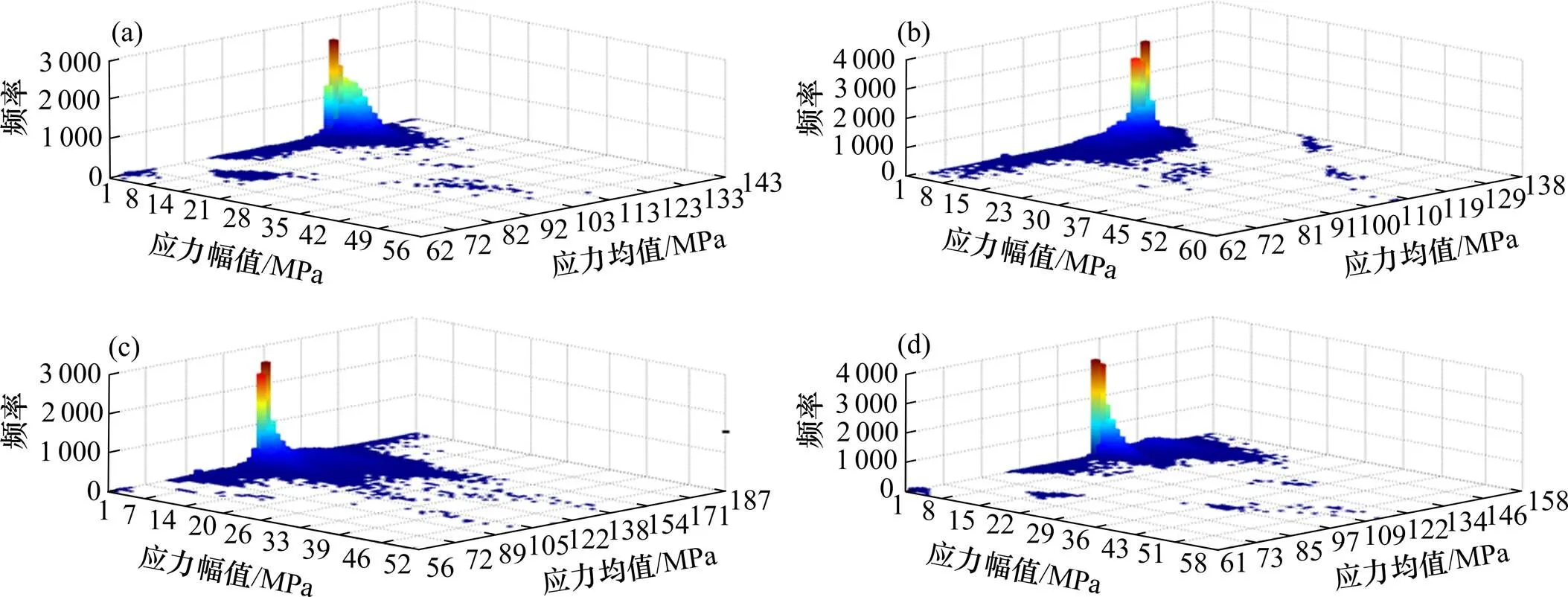
(a) 3点平均值;(b) 测点1;(c) 测点2;(d) 测点3
危险点B在底板分区3个测点应力均值分布有所不同,测点1,测点2和测点3应力均值分别主要分布在104~123 MPa,113~146 MPa和115~140 MPa。3个测点波动中心也不相同,分别依次在66~133 MPa之间、64~179 MPa之间和67~152 MPa之间。
3.2 铆钉疲劳寿命的评估
3.2.1 材料疲劳性能和疲劳参数
1) 参考相关文献[14]得到A6N01S铝合金材料的曲线如图14所示。
2) 铝合金材料疲劳参数,定义如表2所示。
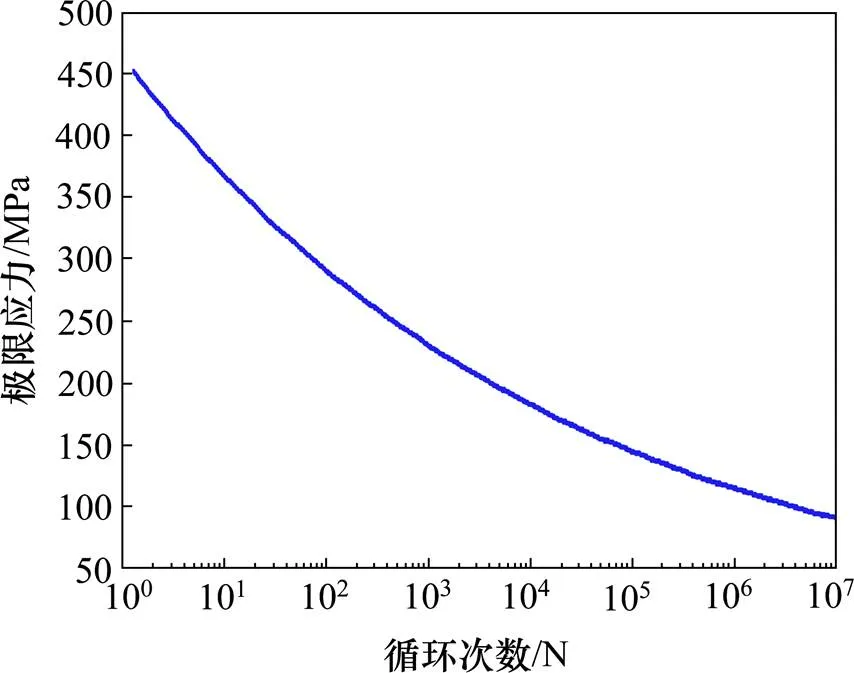
图14 A6N01S铝合金材料的S-N曲线

表2 A6N01S铝合金材料参数[14−15]
3.2.2 二维损伤评估
材料的曲线方程可表示为:

式(2)中:sn,为材料常数。
在第i级载荷幅ai作用下,载荷循环次数达i次时产生的疲劳损伤为:
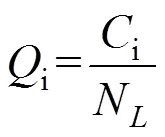
将式(3)代入式(2),于是单个幅值下的疲劳 损伤:
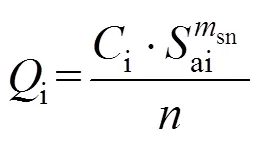
式中:N为该级载荷幅对应的疲劳极限循环数;S为各级载荷水平的幅值;C为各级载荷幅对应的循环次数。
二维载荷谱综合考虑了载荷均幅值的影响,根据Goodman等寿命转换方程将各级载荷转换为对称循环载荷,通过曲线计算疲劳损伤。根据Goodman等寿命转换方程可得[16]:

式中:−1为对称循环载荷幅值;a为载荷幅值;m为均值;u为材料极限强度。
由曲线可计算对应的载荷循环次数N,对应疲劳损伤D,则疲劳总损伤为

3.2.3 铆钉结构疲劳损伤和疲劳寿命计算结果
采用上述3.2.2节中二维载荷均幅值谱的疲劳评估方法,得到铆钉危险点A,B处底板分区3个测点单日疲劳损伤和服役960万km时总疲劳损伤分别如表3~4所示。

表3 铆钉A,B处3个测点疲劳损伤计算结果(单日运行里程:2 100 km)
基于二维疲劳应力谱的疲劳损伤计算结果可知:单日运行里程2 100 km工况下,铆钉结构危险点A 3个分区气动载荷及其平均气动载荷疲劳损伤分别为:01号1.41×10−4,02号1.16×10−4,03号1.22×10−4,平均1.11×10−4,对应的达到动车组设计服役寿命960万km时铆钉结构疲劳总损伤分别为0.64,0.53,0.56,0.51;铆钉结构危险点B 3个分区气动载荷及其平均气动载荷疲劳损伤分别为:01号为4.12×10−5,02号为1.15×10−4,03号为7.85×10−5,平均2.71×10−5,对应的达到设计服役寿命960万km时铆钉结构疲劳总损伤分别为0.19,0.52,0.36,0.13。疲劳总损伤达到1.0,即可以认为铆钉发生了疲劳破坏,从计算结果可以看出,可以认为在高速动车组服役960万km里程寿命内,铆钉能够满足使用要求。

表4 对应的服役960万公里铆钉结构疲劳总损伤计算结果
4 结论
1) 有限元仿真是分析高速列车底板−铆钉结构疲劳损伤与寿命的重要方法。通过对底板−铆钉结构不同方向施加梯度压力加载仿真,得到铆钉结构MISES应力六分量与气动载荷之间数学关系式,为气动载荷谱→应力载荷谱的关系转换做好准备。
2) 对于非对称载荷时间历程,载荷均值变化较大,由于二维载荷谱同时考虑载荷幅值和均值2个参数的影响,故采用二维八级载荷谱对铆钉结构进行疲劳寿命估算可以准确反映铆钉−底板结构的实际受载情况,具备较高的工程参考价值。
3) 由以上计算可知,单日运行2 100 kM工况下,铆钉结构A和B危险点3个分区测点气动载荷及其平均气动载荷疲劳损伤分别为:01号1.41×10−4,02号1.16×10−4,03号1.22×10−4,平均1.11×10−4和01号为4.12×10−5,02号为1.15×10−4,03号为7.85×10−5、平均2.71×10−5,对应的A和B危险点达到高速动车组设计服役寿命960万公里里程时铆钉结构疲劳总损伤分别为0.64,0.53,0.56,0.51和 0.19,0.52,0.36,0.13。疲劳总损伤达到1.0,即认为铆钉结构气动致疲劳失效,由计算结果可知,高速动车组服役寿命内,铆钉结构能够满足使用要求。
[1] 陈福玉. 航空铆接连接件疲劳寿命研究[D]. 南京: 南京航空航天大学. 2011. CHEN Fuyu. Study on fatigue life of aeronautical riveted joints[D]. Nanjing: Nanjing University of Aeronautics & Astronzutics, 2011.
[2] 陈晓丽. 高速列车出隧道空气动力效应数值模拟研究[D]. 兰州: 兰州交通大学, 2016. CHEN Xiaoli. Numerical simulation of aerodynamic effects of high-speed train exiting tunnel[D]. Lanzhou: Lanzhou Jiaotong University, 2016.
[3] 罔旭东. 高速列车车下设备舱底板的可靠性研究[D].北京: 北京交通大学, 2014. WANG Xudong. Reliability study of high speed train equipment bay bottom plates[D]. Beijing: Beijing Jiaotong University, 2014.
[4] 余思均. 高速列车气动载荷车体疲劳强度研究[D]. 成都: 西南交通大学, 2011. YU Sijun. Study on the fatigue strength of high speed train aerodynamic load car body[D]. Chengdu: Southwest Jiaotong University, 2011.
[5] 许乐乐. 基于疲劳的铝合金板件无铆钉铆接接头布置规律研究[D]. 长春: 吉林大学, 2016.XU Lele. Research on arrangement regularity of rivet less riveted joints of aluminum alloy plates based on fatigue[D]. Changchun: Jilin University, 2016.
[6] 李风, 陈海燕, 张毅. 铆钉搭接头疲劳强度曲线的研究[J]. 机械强度, 2002, 24(3): 453−454. LI Feng, CHEN Haiyan, ZHANG Yi. Study on the fatigue strength curves for riveted lap joints[J]. Journal of Mechanical Strength, 2002, 24(3): 453−454.
[7] Urban M R. Analysis of the fatigue life of riveted sheet metal helicopter airframe joints[J]. International Journal of Fatigue, 2003(25): 1013−1026.
[8] Blanchot V, Alain Daidie A. Riveted assembly modeling: Study and numerical characterization of a riveting process[J]. Materials Processing Technology, 2006(180): 201−209.
[9] Szymczyk E, Derewoko A, Jachimowicz J. Analysis of displacement and stress distributions in riveted joints[C]// III European Conference on Computational Mechanics Solids, Structures and Coupled Problems in Engineering, 2006: 434.
[10] 程祖锋, 师欢欢, 徐光兵. 基于ABAQUS的深基坑变形和内力三维有限元分析[J]. 煤炭工程, 2013, 45(9): 119−121. CHENG Zufeng, SHI Huanhuan, XU Guangbing. 3D finite element analysis of deformation and internal force of deep foundation pit based on ABAQUS[J]. Coal Engineering, 2013, 45(9): 119−121.
[11] 李妍. 基于ANSYS软件的接触问题分析及在工程中的应用[D]. 长春: 吉林大学, 2004. LI Yan. The contact element analysis and application in engineering based on the ANSYS software[D]. Changchun: Jilin University, 2004.
[12] 毛贺. 高速列车载荷谱编制方法的研究[D]. 北京: 北京交通大学, 2009. MAO He. Research on the method of compiling load spectrum of high-speed train[D]. Beijing: Beijing Jiaotong University, 2009.
[13] 宋烨. 动车组铝合金车体疲劳寿命评估理论与试验研究[D]. 成都: 西南交通大学, 2016. SONG Yi. Evaluation theory and experimental study of emu carbody fatigue life[D]. Chengdu: Southwest Jiaotong University, 2016.
[14] 陈书翔, 王飞, 寇福俊, 等. 服役后的A6N01S铝合金型材焊接接头组织与性能研究[J]. 轻合金加工技术, 2015, 43(8): 64−68. CHEN Shuxiang, WANG Fei, KOU Fujun, et al. Study on microstructure and properties of welded joints of a6n01s aluminum alloy profiles after service[J]. Light Alloy Processing Technology, 2015, 43 (8): 64−68.
[15] 陈辉刚. 高速列车用A6N01S-T5铝合金及其焊接接头高寒条件下的性能[J]. 电焊机, 2016, 46(9): 77−82 CHEN Huigang. Performance of the A6N01S-T5 aluminum alloy and the welding joint for high speed train at low temperature[J]. Electric Welder, 2016, 46(9): 77− 82.
[16] 宋振伟, 曹俊伟, 刘玲, 等. 船用钛、钢法兰连接螺栓的疲劳强度性能分析[J]. 中国舰船研究, 2018, 13(增1): 106−110. SONG Zhenwei, CAO Junwei, LIU Ling, et al. Analysis of fatigue strength of titanium-steel flange connection bolts in ship[J]. China Ship Research, 2018, 13(Suppl 1): 106−110.
Research on fatigue characteristics of high speed train fan bottom plate rivets under alternating aerodynamic load
FU Shaoqing1, 2, LIU Kai1, 2, XIONG Wei1, 2, ZHOU Wei1, 2, 3
(1. School of Traffic and Transportation Engineering, Central South University, Changsha 410075, China; 2. Key Laboratory of Traffic Safety on Track of Ministry of Education, Changsha 410075, China; 3. Joint International Research Laboratory of Key Technology for Rail Traffic Safety, Changsha 410075, China)
Aiming at the fatigue damage of high-speed train floor-rivet structure under alternating aerodynamic load in a complex service environment, a fatigue load spectrum compilation and damage assessment method based on the service aerodynamic load-rivet structure stress distribution was proposed. First, a finite element model of the train floor/rivets/beam-slab was established, and the mechanism of the influence of the bending effect of the bottom plate on the strength of the rivet structure under aerodynamic loads in different directions was analyzed, and the nonlinear transfer factor of the aerodynamic load-rivet stress was obtained; The pressure measurement points capture the aerodynamic load spectrum of the bottom plate service. Finally, the dynamic stress load spectrum of the rivet structure was compiled based on the service aerodynamic load spectrum andthen on-linear transfer factor, and the two-dimensional eight-level load spectrum of the rivet structure was established based on the rain flow count and Miners cumulative damage criterion. The fourth strength theory stress criterion was used for fatigue damage assessment. The conclusions show that when the high-speed EMU reaches the service life of 9.6 million km under alternating loads, the total fatigue damage of the two dangerous points of the rivet structure under the effects of aerodynamic loads and average aerodynamic loads in the three zones are 0.64, 0.53, 0.56, 0.51 and 0.19, 0.52, 0.36, 0.13. The total fatigue damage reaches 1.0, which means the fatigue failure of the rivet structure under aerodynamic load is considered. From the calculation results, it can be known that the rivet structure can meet the service requirements during the service life of the high-speed EMU.
high-speed train; aerodynamic load; rivet structure; load spectrum; fatigue damage assessment

U266
A
1672 − 7029(2020)12 − 3003 − 10
10.19713/j.cnki.43−1423/u.T20200108
2020−02−14
国家重点研发计划资助项目(2017YFB1201201)
周伟(1982−),男,湖南长沙人,副教授,博士,从事轨道交通装备疲劳载荷谱在途监测与寿命评估;E−mail:zhou_wei000@126.com
(编辑 涂鹏)
