铁路道砟形态特征的统计分析与几何重构

2021-01-08肖军华郭佳奇薛立华

同济大学学报（自然科学版） 2020年12期

肖军华，郭佳奇，张德，3，薛立华

（1.同济大学上海市轨道交通结构耐久与系统安全重点实验室，上海201804；2.同济大学道路与交通工程教育部重点实验室，上海201804；3.上海公路桥梁（集团）有限公司，上海200433）

铁路有砟道床作为一种由道砟颗粒组成的散体结构层，在列车重复荷载作用下，会产生道床颗粒间相互错位和重新排列，甚至道砟颗粒的破碎和粉化，使其力学性能逐渐退化。由于道砟颗粒的形态、尺寸等对颗粒力学行为以及道床的变形和劣化均有重要影响。近年来，对道砟颗粒不规则三维形态特征的定量描述日渐成为研究热点。

目前工程中对道砟形态的控制主要以级配粒径为主，并辅以针状指数与片状指数来评估颗粒形态。受限于规准仪测量手段，上述指标仅能从宏观上量化道砟集料整体形态特征，精度较低［1］，不能准确描述单一道砟颗粒的形态、棱角等几何形态特征。因此，有必要在考虑道砟不规则形态及随机分布等离散特性的基础上，对铁路道砟形态特征进行量化统计研究。

在道砟颗粒形态特征分析方面，Bettina等［2］指出主要有三层尺度：整体形态（Form）、棱角及圆（球）度（Angularity/Roundness）以及纹理（Texture）。Pen等［3］指出整体形状（Form）和棱角（Angularity）可作为描述颗粒形态的相互独立的指标，其相互独立是因为每个指标都能在不影响其他指标的前提下变化。其中，在对颗粒整体形态的描述中，如果Φ1、Φ2、Φ3分别表示完全包含颗粒的矩形框［4］的最长、中间和最小尺寸，则将上述三个指标作为描述道砟颗粒三维尺寸的基本形态指标，分别命名为长轴、中轴、短轴。利用Φ1、Φ2、Φ3中两指标间的相互比例关系，能够得到描述颗粒整体形态特征的其他指标［5］，如伸长率（Φ2/Φ1）、扁平度（Φ3/Φ2）、长细比（Φ3/Φ1）。

除了上述整体形态指标，道砟颗粒的棱角性也会影响道砟颗粒间咬合力以及接触力网络的各向异性分布，从而导致道床的剪切强度的变化［6］。YAN等［4］采用球度指数和棱角指数评估颗粒宏观和细观形态特性，其中球度指数与颗粒的三维尺寸相关，描述不规则颗粒与球体的近似程度；棱角指数（angularity index，AI）是基于二维图像分析得到的描述道砟截面棱角特征的指标［7］，通过对道砟内接多边形的内角角度变化值来估算。采用棱角指数评价颗粒三维棱角特征的过程中，二维截面选取具有随机性，可能会使得所生成的3D形态不符合实际［8］；并且二维指标忽略了点与点在三维空间中的相互关系，而颗粒棱角与空间点及其周围点的相对位置有关。因此，需要建立新的评价指标来描述道砟颗粒三维局部形态特征。

目前国内外学者依靠获取真实道砟形状数据尽可能还原颗粒形态特征，并且随着技术的进步，道砟颗粒形状数据的获取也由二维影像技术逐步发展到三维技术（机械式以及激光式）。DESCANTES［9］等利用自由下落过程中的道砟颗粒多角度影像，获取了大量道砟颗粒的二维廓形。MORA［10］等基于数字图像处理技术（digital image processing，DIP）提出了基于颗粒二维图像面积的颗粒三维尺寸修正方法。Rao［11］、Huang［12］以及 Tutumluer等［13］采用图像分析系统UIAIA获取道砟颗粒多角度二维轮廓，通过正交成像还原道砟三维外形。在此基础上，边学成等［14］将基于二维轮廓正交重构的三维道砟颗粒成功引入离散元数值模拟。付招兴［15］则基于数字图像处理技术获取道砟平面几何数据，分析了颗粒不规则形态特征。Nishiura等［16］通过3D机械式扫描得到道砟颗粒表面顶点坐标，用三角形平面连接表面顶点形成的凸多面体模拟道砟。近年来，随着3D激光扫描技术的发展，KIM［17］将其引入到碎石颗粒的三维轮廓分析研究中。井国庆［18］等结合3D扫描技术与洛杉矶磨耗试验分析了道砟的主要劣化形式以及磨耗率的影响因素。徐旸［1］、张徐［19］等通过3D激光扫描获取铁路碎石道砟颗粒表面点云坐标用于道砟破碎及其他力学行为仿真分析。

上述学者使用数字化测量手段获取了一定数量的道砟颗粒的三维形状，但均未从概率统计的方面来描述或者重构颗粒形态。此外，国内外仅有少量文献［20-21］基于碎石道砟形态参数的概率密度分布模型进行道砟颗粒重生成并用于仿真模拟（例如离散元法模拟），但其仅考虑了颗粒整体形态参数，且未给出具体的形状系数的求解方案。再者，为了研究道砟力学性能，需要建立表征真实道砟颗粒形状的道砟样本并用于数值仿真，仅使用3D扫描获取的道砟颗粒形态数据所构建的有限的道砟样本库，在使用时对道砟颗粒形态特征的要求存在一定局限性。综上，需要建立一种方法生成能够满足真实形态特征统计分布的大量道砟颗粒。

本文通过引入道砟整体形态特征指标，提出道砟局部形态特征指标，统计建立了上述指标的概率密度分布函数。采用本征正交分解（proper orthogonal decomposition，POD）提取了表征颗粒形态特征的基向量，采用径向基（radial basis function，RBF）神经网络寻找基向量与样本形态指标间的映射关系，完成了基于颗粒形态描述指标概率密度函数的道砟样本建立。最后，以铁路一级碎石道砟为例，分别重构了600及4000个道砟颗粒组成的样本。

1 道砟整体形态特征的扫描统计分析

1.1 道砟三维轮廓表面形态数据获取

已有研究［20］对比不同颗粒数（160、300、400、500、800以及975颗）组成的道砟试样后指出，当颗粒数量大于400时，不同数量颗粒组成的道砟样本统计得到的表征数据样本主要形态特征的基向量间的差异可以忽略不计。因此，本文根据《铁路碎石道砟》［22］（TB/T 2140-2008），按照一级碎石道砟级配要求，采用标准方孔筛筛取50kg碎石道砟试样（包含584个道砟颗粒），该试样同时能够满足道砟直剪试验［23］、三轴试验［24］对试验用道砟重量的要求，扫描试验道砟样本级配曲线如图1所示。

图1 道砟3D激光扫描试验级配曲线Fig.1 Gradating curves of 3D laser scanning test for ballast

对各个级配下的颗粒进行编号，编号形式为No.m～n#，其中m表示不同级配范围对应分类编号，0～16mm、16～25mm、25～35.5mm、35.5～45mm、45～56mm、56～63mm级配范围内的道砟分别编为1～6#；n表示该级配下的道砟颗粒编号（如图2a）。

采用Creamform手持激光扫描仪对道砟颗粒进行3D激光扫描获取颗粒表面轮廓点云数据（如图2b所示）。扫描原理为：激光束通过图2b中黑色定位标记点和道砟表面点的相对位置确定坐标具体数值，经激光发射器发出激光在道砟表面反射，采集坐标数据传输到电脑，记录道砟颗粒三维轮廓表面点云坐标。为了确保道砟颗粒表面均被扫描到，作者对每个道砟都进行了两次扫描。由于第一次扫描颗粒时存在一定盲区，第二次扫描时将颗粒进行一定转动，将第一次扫描中的盲区进行补充扫描，并保证两次扫描有公共区域，根据公共区域内点的相对位置关系将两次扫描结果进行拼接，从而最终完成颗粒点云扫描。图2c中取各级配真实颗粒与扫描结果进行对比，表明3D激光扫描能够准确获取道砟颗粒轮廓表面点云坐标数据。

1.2 道砟整体形态特征的指标

参考文献［3-4］，引入长轴Φ1、中轴Φ2、短轴Φ3以及球度指数界定道砟颗粒整体外形特征。其中，Φ1表示颗粒两表面点之间最长轴；Φ2表示垂直于Φ1的最大投影面（中轴存在的面，与Φ1轴交于I点）的最长距离，并且Φ2值本质上反映了道砟颗粒的过筛粒径；Φ3是垂直于Φ1的最大投影面中垂直于Φ1和Φ2的最长距离，三条特征轴位置如图3所示，其中Φ1对应P+P-、Φ2对应AC、Φ3对应BD。Φ1、Φ2、Φ3可表示如下：

球度指数描述不规则颗粒与球体的近似程度，由式（2）表示。由于其3次方在数值上等于伸长率（Φ2/Φ1）和长细比（Φ3/Φ1）的乘积，为便于描述，本文选取球度指数Sp三次方用于道砟整体形态特征统计：

图2 3D激光扫描Fig.2 3D laser scanning of ballast particles

3Φ×Φ

图3 道砟颗粒长轴、中轴、短轴计算示意图Fig.3 Schematic diagram of long axis,middle axis and short axis of ballast

1.3 道砟整体形态特征的概率密度分布模型

通过对3D激光扫描得到的所有道砟颗粒的表面轮廓形态点云数据进行处理。对Φ1、Φ2、Φ3以及Sp3进行统计计算。基于对所有颗粒形态特征指标参数的统计分析，建立道砟整体形态特征指标的概率密度分布模型，如图4所示。

图4 道砟整体形态特征参数统计分布直方图及拟合概率密度曲线与函数Fig.4 Histogram,fitting probability density curves and function of the statistical of ballast morphological feature indices

2 道砟局部形态特征的扫描统计分析

对道砟颗粒局部形态特征的描述在于对棱边和尖角部位的表征。现有文献［4］采用棱角指数描述颗粒局部棱角特性。棱角指数首先取颗粒一方向二维投影平面视图中近似多边形颗粒轮廓计算相邻顶点夹角。通过落在不同区间内角度的比例来评估颗粒轮廓的棱角起伏变化状况。

然而，采用棱角指数评价颗粒三维棱角特征的过程中，颗粒摆放以及二维截面选取角度均是人为的，若截面选取不当会导致该指标不能够反映颗粒间棱角特征的差异。因此，本文提出了曲率指数（curvature index，CI）来定量描述道砟颗粒棱角特性。下面首先验证了采用离散点云局部曲率识别道砟颗粒棱角的有效性，而后提出了曲率指数的计算方法，并同时计算颗粒的CI与AI值进行对比，验证曲率指数对于描述颗粒局部棱角特征的优势性。

2.1 基于离散点云局部曲率识别道砟颗粒棱角

道砟扫描点云数据在颗粒表面表现为一组离散的轮廓点样本，计算各点局部曲率首先要确定每点对应的表面法线。确定表面一点法线近似于估计表面的一个相切面法线，可以转换为分析一个协方差矩阵的特征矢量和特征值，这个协方差矩阵从查询点的近邻元素中创建，它能够表明一定区域内点云的起伏变化。更具体地说，对于每个点Pi，所对应的协方差矩阵C如下：

式中：k是Pi近邻点数量（本文计算时取9个邻近点）是最近邻元素的3D质心；λj是协方差矩阵第j个特征值；v→j是第j个特征向量。

λj衡量Pi沿着相应的特征向量 v→j方向的变化，标记特征值使得λ0≤λ1≤λ2。根据Pi点及相应邻近点，由最小二乘法拟合过Pi点平面T（x）：（x-Pi）·v0=0。因此，v0近似于Pi处的表面法线。相应地，λ0定量描述了沿表面法线的变化。在大小为k的邻域中的点P处定义表面变化σk(pi)，即

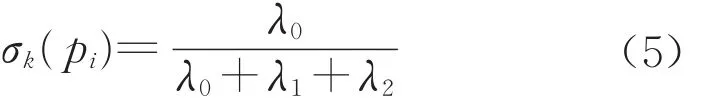
σk（pi）趋于0，表示点Pi及其k个近邻点组成的采样点所对应的曲面接近于平面。给定k的选择，每个顶点归因于法向量和表面变化值，将该表面变化值σk（pi）定义为局部曲率。

计算每个颗粒点云坐标对应的局部曲率，以方位角和仰角为横、纵坐标轴，将三维空间每点的曲率在平面展开。图5以编号3-149#道砟颗粒为例，叙述离散点云局部曲率对道砟棱角的识别过程。

图5中深色部分为局部曲率较高点，当深色部分连续成条时表明该区域颗粒表面存在棱边，如图5中左边颗粒1～3所标注棱边对应的深色曲率点集。当3条连续深色部分交汇，则表明该区域颗粒表面存在棱角，如图中灰色圈部分。上述分析表明：颗粒点云离散点曲率值及分布能够有效描述和识别道砟棱边和棱角特征。

图5 离散点云局部曲率对道砟棱角的识别Fig.5 Identification of the corners and corners of the local curvature of discrete point clouds

2.2 基于离散点云局部曲率描述道砟颗粒棱角特征

进行3D激光扫描所获取的道砟颗粒轮廓点云，每个颗粒包含几万到十几万不等的三维点坐标。为提高离散点局部曲率计算效率，对所有颗粒点云进行标准化处理，并采用球坐标表征道砟颗粒形态。文献［20］中分析道砟颗粒点云简化时发现，当颗粒点云数降至800个时所表征的简化颗粒与原始颗粒之间的误差已降至5×10-5。因此，本文颗粒点云标准化的点云数取为800。首先将所有颗粒的形心移动到坐标原点，旋转点云使长轴与Z轴平行。然后在初始扫描点云基础上（如图6 a），采用排斥点迭代算法在单位球表面生成具有均匀密度方向角和仰角的800个点（如图6 b）及射线，保留道砟初始点云中处于射线上的点，从而将道砟颗粒表面点云数量简化为800个（如图6 c）。

图6 道砟颗粒点云坐标标准化处理过程Fig.6 Normalization process of ballast particle point cloud coordinate

NOURA［20］采用聚类算法识别颗粒轮廓的棱角和面，表明扫描道砟颗粒中属于明显表面平面上的点约占颗粒点云总数的50%～80%。因此，可以认为道砟颗粒点云中至少存在20%的顶点位于棱边或角点上，这些点对应的局部曲率大于处于面上的点的曲率。以编号3-149#颗粒为例，将点云坐标对应曲率按照从大到小排列，提取前20%曲率对应的坐标点，如图7所示。

图7 No.3-149#道砟颗粒前20%曲率对应的坐标点Fig.7 No.3-149#coordinate point corresponding to the first 20%curvature of the ballast particles

由图7可知，曲率前20%所对应的点基本位于颗粒的棱边和角点上，可以勾绘出颗粒基本形态，能够反映道砟局部形态特征特别是棱角特征，并且此规律同样适用于扫描得到的其他道砟颗粒。因此，本文将颗粒简化点云对应曲率由高到低排列，取前20%的点曲率求和，构造道砟三维局部形态描述指标——曲率指数（CI）。本文中颗粒点云进行了标准化处理后每个颗粒均包含800点云，所以CI计算时将各点曲率由高到低排列，取前800×20%=160个点曲率求和。即

式中：ρi按照降序排列，包含 800 项且ρ1≥ρ2≥···≥ρ800。

图8列举了颗粒整体形态指标Sp3相近情况下道砟颗粒CI与AI计算值。由图8可以看到，从a到c颗粒CI值的变化较AI值更为显著，表明曲率指数对颗粒整体表面棱角特征的变化更为敏感，也较传统基于二维轮廓面的棱角特性指标AI更能描述颗粒局部棱角特征。

图8 整体形态指标相近情况下颗粒CI与AI值对比Fig.8 Comparison of particleCIand AIvalues in the case of similar overall morphological indicators

为此，选取CI作为道砟局部形态特征指标，并统计计算其概率密度分布函数，如图9所示。

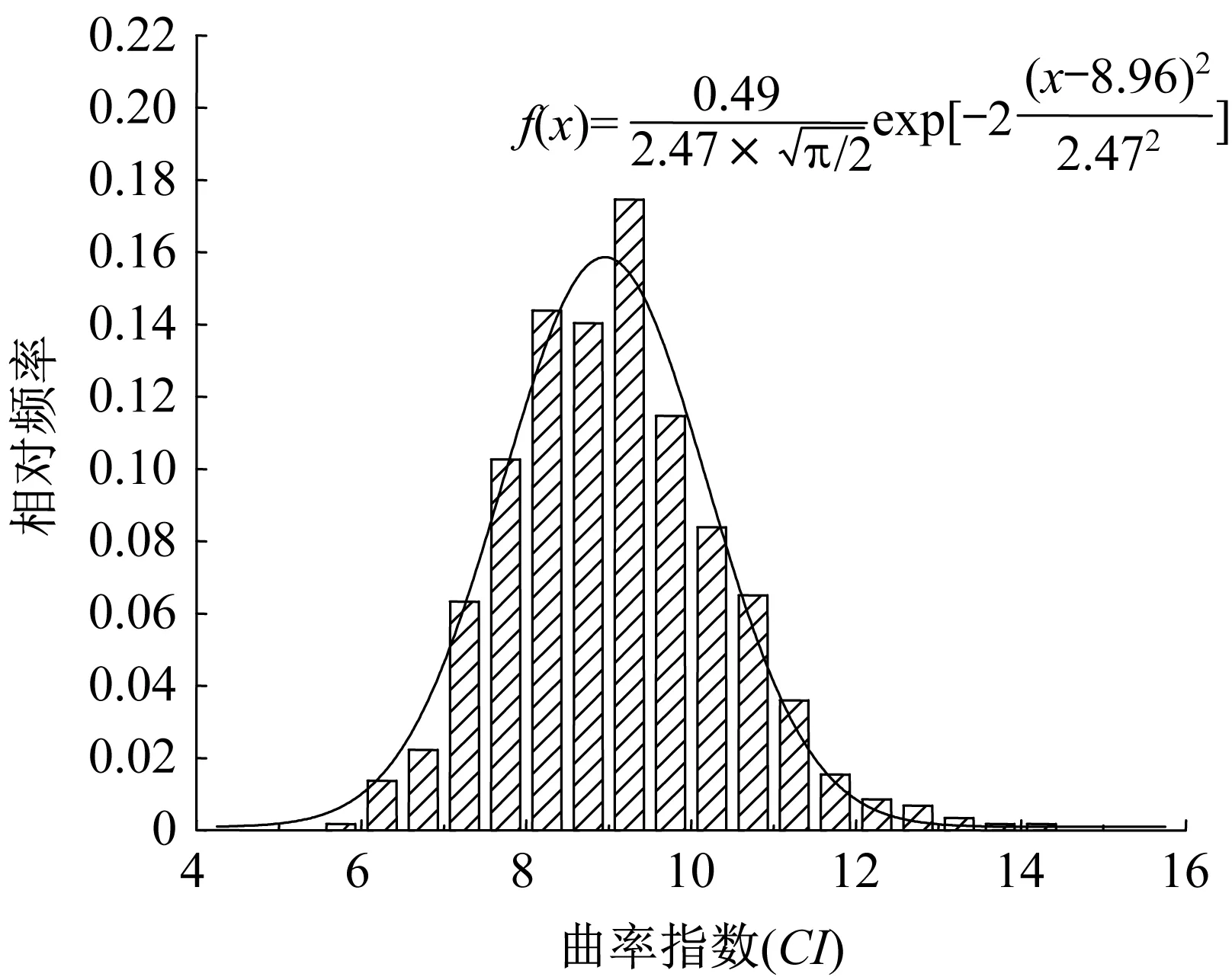
图9 曲率指数统计分布直方图及拟合概率密度曲线与函数Fig.9 Curvature index statistical distribution histogram and fitting probability density curve and function

3 基于本征正交分解与径向基神经网络的道砟颗粒样本重生成

获取道砟颗粒整体与局部形态特征指标的概率密度分布后，为生成满足特定形态特征的任意数量的道砟颗粒样本，需要建立颗粒形态指标与颗粒点云间的关系。然而，道砟颗粒点云在初始全局坐标系投影下数据量大且无序，为此，本文采用本征正交分解（proper orthogonal decomposition，POD）［25］由局部映射解析出表征道砟形态主要模态特征的基向量，从而对道砟试样形态数据进行降维，并将降维后的基向量与形态扩展系数组合来重构颗粒形态。根据径向基（radial basis function，RBF）神经网络［26］学习，获取颗粒形态扩展系数与形态指标间的映射关系，可根据目标形态指标概率密度分布函数确定对应的形态扩展系数，实现任意数量道砟样本的重生成。

3.1 道砟形态在基向量下的表征

本征正交分解（POD）是模型降阶的一种基本方法，能从扫描道砟样本形态数据中提取主要特征。假设数据集有m个样本点，x1，x2，···，xm，其中xi∊Rn。对于这m个样本，可以利用奇异值分解方法获得一组有序的正交基向量｛φi｝（i=1，2，···，m），则对任意样本向量 xi∊Rn，有 xi=c1iφ1+c2iφ2+···+cmiφm（i=1，2，···，n），其中cji=φiTxi。若选择前k个基向量来逼近样本向量xi，则有xi（k）=c1iφ1+c2iφ2+···+ckiφk，即可通过k个系数的取值来表征颗粒形态，它包含了x在这个数据集中大部分的特征信息。令

I（k）表示所选择的k维POD基向量｛φi｝（i=1，2，···，k）近似代表的原始向量的特征，其中λi（i=1，2，···，n）为相关矩阵按降序排列的特征值。道砟点云数据由2.2节中标准化处理后，每个颗粒的表面轮廓形态可用800个三维点坐标表示。将点云坐标由直角坐标（x，y，z）转化为球坐标（r，θ，φ），其中径向距离r为原点与表面轮廓点P间距，方位角θ为原点到点P的连线在xoy平面的投影线与正x轴的夹角，仰角φ为原点到点P的连线与正z轴的夹角的余角。

点云数据转化到球坐标系后，由于每个颗粒的（θ，φ）排列均固定不变，所以仅分析不同方向的径向距离r，就能量化表征颗粒形态。汇总584个扫描道砟颗粒的形态信息，获得800×584矩阵，矩阵中每列包含一个颗粒在800个方向上的径向距离值。

用rij表示颗粒j沿i方向的径向距离，其中每一行包含在一个方向上测量的m（本文m=584）个颗粒的半径，每一列包含m个颗粒中的一个颗粒沿着d（本文d=800）个方向中每一个方向的半径。将各个方向上所有颗粒的径向距离进行平均，即

如图10所示，各方向上平均径向距离组成的颗粒接近于椭球体，该颗粒长轴、中轴、短轴的长度分别为：Φ1=5.437 0cm，Φ2=2.973 8cm，Φ3=2.772 4cm。

图10 各个方向上平均径向距离组成的颗粒Fig.10 Particles consisting of average radial distances in all directions

定义每个道砟颗粒与各个方向上平均径向距离组成的颗粒之间的差异：

计算得到Δrij的800×584矩阵A，通过在平均径向距离上累加不同的Δrij，可以实现不同形态道砟颗粒的差异化表征。采用POD从Δrij数据样本中计算表征道砟颗粒形态特征的基向量，即式（10）中协方差矩阵的特征向量和对应系数矩阵（式（11）），按照式（12）取前k阶重构颗粒形态，因而真实形态和近似形态之间的相对偏差采用式（13）度量。

式中：A为颗粒Δrij输入矩阵；r为矩阵A的秩；U（U（k））表示特征向量（在k维截断）；D=d（i）表示协方差矩阵AAT的特征值；C（C（k））表示包含所有系数的矩阵（在k维截断）；k表示选择的基向量的维数；Ak表示k维基向量重构的形态数据；E（k）为与k维基向量对应的相对误差，随k的增加而减小，并在k=m时等于0。

图11表示式（13）定义的相对误差随着基向量维数增加而变化的情况。

图11 不同维数基向量所描述的颗粒形态特征的误差Fig.11 Errors of particle morphological features described by different dimensional basis vectors

对于道砟颗粒j，按照式（14）计算不同方向的径向距离rj，辅以对应的（θ，φ），就能生成颗粒点云坐标。

由式（14）知，构造道砟颗粒三维点云转换为生成每个颗粒径向距离r对应的形态扩展系数。表1列出了不同维数基向量所表征的颗粒形态信息。

图11和表1说明，基向量维数越多，所描述的颗粒形态特征的误差越小。1维基向量包含超过50%的形态信息，相比之下，剩余维度基向量则是对颗粒在空间某方向进行的局部扩展。

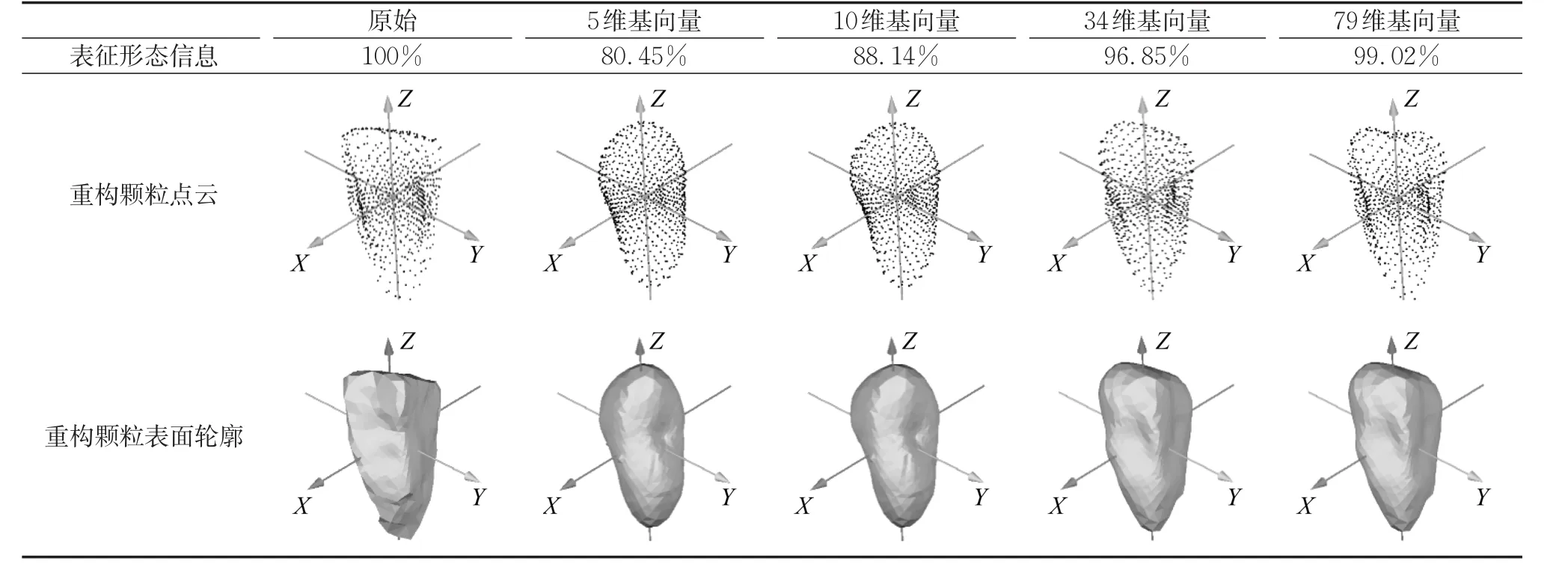
表1 不同维数基向量重构的道砟颗粒形态及所表征的形态信息（以No.3-149#颗粒为例）Tab.1 Morphology of the ballast particles reconstructed by different dimensional basis vectors and the morphological information characterized(No.3-149#particles as an example)

因此，POD能够使用减少维数的基向量来生成与真实道砟形态相当的颗粒。特征值代表对应基向量方差，近似颗粒形态包含原始颗粒形态的特征信息越多，方差越大，反之则越小。如果基向量对应的特征值小于1，说明其仅能解释1阶形态特征因子的方差，甚至还不能完全解释。因此，本文在POD分析中，以基向量对应特征值大于1作为保留基向量维数的条件，抽取34维基向量应用于道砟颗粒重构分析，这34维基向量所对应的特征值均大于1。如图11所示，34维基向量能够描述道砟超过96%的形态特征信息。图12中列举了不同级配粒径范围内原始颗粒与34阶基向量重构颗粒的轮廓对比。

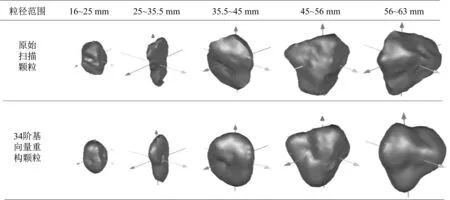
图12 不同级配原始颗粒与重构颗粒对比Fig.12 Comparison of original particles and reconstructed particles with different gradation

3.2 基于形态指标概率密度分布函数的道砟样本重生成

为使重构的任意N个颗粒能够满足指定的形态指标概率密度分布，需要明确形态指标与形态扩展系数之间的关系。扫描后统计的各个形态指标（长轴、中轴、短轴、球度指数、曲率指数）的概率密度分布函数相互独立，但颗粒形态指标之间存在相关性，即颗粒Φ2与存在组合关系。另外，由式（14）可知，任意一个重构道砟颗粒rj对应一组c0j～ckj，重构颗粒的形态指标组合与形态扩展系数相对应，即

对于服从一定形态指标概率密度分布的扫描道砟试样而言，颗粒形态指标的组合关系以及指标与形态扩展系数间的映射关系均是高度非线性的。为此，本文采用了径向基（RBF）神经网络对扫描样本颗粒形态参数指标间的对应关系进行学习，得到重构道砟颗粒形态指标间组合，获取形态特征基向量对应的形态扩展系数。流程如图13所示。

图13 道砟样本重生成流程Fig.13 Progress of ballast sample regenerating

RBF神经网络是一种三层神经网络，包括输入层、隐含层以及输出层，它将非线性的输入进行高维度映射从而达到线性输出的目的。首先设置隐含层随机中心点c作为“基”，并构造非线性距离函数计算输入层各输入量与中心层映射距离h如下：

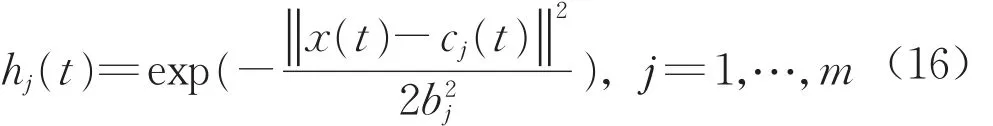
式中：x=［xi］T为网络的输入；网络的隐含层输入为h=［hj］T，hj为隐含层第j个神经元的输出；cj为隐含层第j个神经元高斯基函数中心点坐标；bj为隐含层第j个神经元高斯基函数的宽度。最终将隐含层加权计算得输出为

图13中将中轴指标Φ2作为输入层变量，由所有扫描样本学习输出其余4个指标，从而得到（Φ2、Φ1、Φ3、Sp3、CI）组合。再将（Φ2、Φ1、Φ3、Sp3、CI）组合作为输入层，学习得到构建任意N个颗粒的形态扩展系数C，并根据式（14）完成道砟库重构。

按照上述方法重生成N=600和N=4 000个颗粒组成的道砟样本，将形态特征指标值进行统计，绘制重构颗粒组成的道砟样本形态特征参数的拟合概率密度分布函数，将其与扫描道砟样本的形态特征参数的概率密度分布函数进行比较，如图14所示。

图14 重生成不同颗粒数量的道砟样本特征参数分布对比Fig.14 Comparison of eigenvalue distributions of ballast samples regenerated with different particle numbers

计算扫描样本与重生成样本的形态特征指标分布的概率密度函数中变量（对数正态分布函数的变量指变量的对数）的平均值和标准差，汇总如表2所示。

表2 扫描样本与重生成样本形态特征指标分布的拟合概率密度函数中变量的平均值和标准差Tab.2 The mean and standard deviation of the variables in the fitted probability density function of the scan sample and the regenerated sample morphological feaure index distribution

图14及表2表明，重生成道砟样本形态特征指标分布的拟合概率密度函数中，变量的平均值和标准差与扫描样本接近。这说明，重构道砟样本库特征值的分布函数基本能再现扫描统计分布。