城市轨道交通正线列车故障发生概率预测模型

王镇波，叶霞飞，沈 坚，施董燕

（1.同济大学道路与交通工程教育部重点实验室，上海201804；2.同济大学上海市轨道交通结构耐久与系统安全重点实验室，上海201804；3.上海申通地铁集团有限公司技术中心，上海201103）

城市轨道交通列车故障是造成正线运营延误甚至中断的主要原因之一［1-2］，不仅影响乘客正常出行，还埋下许多安全隐患。为此，《地铁设计规范》［3］规定正线上每隔5～6座车站或8～10 km设置停车线，以确保列车在正线任何位置发生故障后，将其处理下线的救援时间控制在30 min以内。但是整个城市轨道交通生命周期内因停车线起作用而降低故障列车对正线运营影响程度所带来的效益是否高于额外修建停车线所产生的土建及维护成本一直是个值得关注的问题。其中，列车故障发生概率的高低对正线运营的影响程度差异很大，应是设置停车线时除了救援时间之外需要考虑的一个重要参数。因此，深化列车故障发生概率的合理预测方法意义重大，可为停车线设置方法的进一步完善提供列车故障发生概率参数取值的依据。

在理论上，一起列车故障就是一次贝努利试验的结果，每一列车在开行某个班次时，它如果顺利完成即成功，如果发生列车故障即失败。而城市轨道交通列车每日发生故障一般属于小概率事件，这使得出现一次失败所需的贝努利试验次数十分巨大。针对这一特点，很多学者往往采用离散型分布中的泊松分布［4］或负二项分布［5-6］构建模型，其中泊松分布要求均值等于方差，负二项分布则适用于方差明显大于均值的情况。随着研究与应用的进一步深入，出现了有零过多现象的数据，如每列车短时期内发生故障的次数，这种数据中0的个数要明显多于由泊松分布与负二项分布随机产生的个数，因而采用零膨胀泊松分布［7-8］、零膨胀负二项分布［9］的研究逐渐兴起。

考虑到在停车场等非正线上发生的列车故障不影响列车正常运营，本文选择城市轨道交通列车在正线上发生故障的概率作为重点研究对象（以下提及的列车故障发生概率若无特别说明，均指城市轨道交通列车在正线上发生故障的概率）。首先定性分析列车故障发生概率的主要影响因素，之后基于实际数据生成包含这些影响因素的离散型数据集，在此基础上从泊松分布、负二项分布、零膨胀泊松分布、零膨胀负二项分布中选择合适的分布及可能的函数形式构建备选模型并标定，最后通过模型比选确定最终的城市轨道交通正线列车故障发生概率预测模型。

1 列车故障发生概率主要影响因素

从产品构成的角度来看，城市轨道交通列车由多节车厢串联而成，任一车厢的部件出现损坏时，均视作该列车的一起故障，而编组越多的列车拥有的部件会越多，出现故障的可能性也就越高。因此城市轨道交通列车的编组数应对其故障发生概率产生显著影响，且列车故障发生概率会因列车编组数增加而变高。

从产品使用的角度来看，城市轨道交通列车具有系统集成度高、设备种类多、设备工况复杂等特点，刚投入使用的列车需要经历一段部件磨合期才能达到最佳使用状态［10］，所以整列车的故障发生概率在使用初期往往会比较高。在部件磨合期结束后，整列车的故障发生概率应处于相对较低的阶段，之后随着列车走行公里的累计，部件老化及磨损的问题则可能会使整列车的故障发生概率有所回升。由此可见，城市轨道交通列车自投入运营开始的累计走行公里应对其故障发生概率产生显著影响，且列车故障发生概率会因累计走行公里增加而呈现先高后低再高的特点。

需要注意的是，城市轨道交通列车在整个寿命周期中会经历各种类型的维修，目前计划修是国内外城市采用的主流列车维修方式［11-13］，即只要设备到了规定时期就需进行维修与替换。在国内计划修的维护规程中，架修和大修均需要对车辆解体并更换一系列设备重新组装，架修涉及车辆的大部分部件，而大修则是全面性深层修理［10］。经过架修或大修后的列车几乎接近新车，所有因累计走行公里产生的部件损耗及老化将全部消除，应对其故障发生概率产生显著影响。

考虑到城市轨道交通列车每日发生故障一般属于小概率事件，需要在一定的走行公里范围内对其进行观察。根据《地铁设计规范》［3］，新建地铁工程的车辆架修和大修周期分别应为60万km、120万km，在无法得到详细行车资料的情况下可分别采用5年、10年的时间间隔，则走行公里与时间间隔之间的关系可依此推算为12万km对应1年。为此，本文在生成离散型数据集时选择以12万km为间隔划分每列车的累计走行公里，观测其在每个12万km内发生故障的次数。在这个观测范围下，可以减小季节气候、列车拥挤度［8，14］等因素对列车故障发生概率预测精度的影响程度。

综上所述，最终通过定性分析得到的列车故障发生概率的主要影响因素为列车编组数、累计走行公里、架修或大修经历。下面将基于实际数据生成包含上述影响因素的离散型数据集。

2 数据来源及处理

2.1 数据来源

本文数据由某城市轨道交通公司提供，具体包括全网各线列车的首次正式投入使用日期、2011至2019年间架修和大修记录、2017至2019年间故障记录（含故障发生的时间、地点及原因）、编组情况以及全网各线2011至2019每年总列车运营里程。

经过初步数据整理，共有910列对象列车、600起在正线上发生的列车故障记录。首先，剔除了其中投入运营时间不明（35列）、列车编组有变更（2列）、架修和大修记录缺失（76列）的对象列车。其次，考虑到因偶然因素造成的列车故障随机性太强，为了避免各类偶然因素对主要影响因素的干扰，剔除了因异物卡阻（30起）、乘客冲门（15起）、其余偶然因素（56起）造成的列车故障记录。最终保留了797列对象列车、499起列车故障记录作为后续研究的基础数据。

2.2 数据处理

基础数据未直接给出列车的累计走行公里，需要通过列车的累计运营时间乘以日均走行公里进行推算。

列车的累计运营时间可根据列车的首次正式投入使用日期、架修和大修记录确定。首先用列车首次正式投入使用日期作为累计运营时间的起始日期，之后查询列车是否有过架修或大修经历，如果有，则累计运营时间的起始日期需更换为列车完成最近一次架修或大修后正式投入使用的日期，以重置其累计运营时间。至于是否应对架修后的列车和大修后的列车进行区分，考虑到架修和大修的本质都是对列车部件进行更新，只是大修更全面彻底，所以如果造成列车故障的部件均在架修和大修时涉及检修和更换，则无需对两者进行区分。为此，对列车故障成因进行统计，如图1所示。基于文献［15］并结合图1可知，除“其他”以外的列车故障成因所涉及的部件均会在架修和大修中进行检修和更换，故本文不再对两者进行区分。

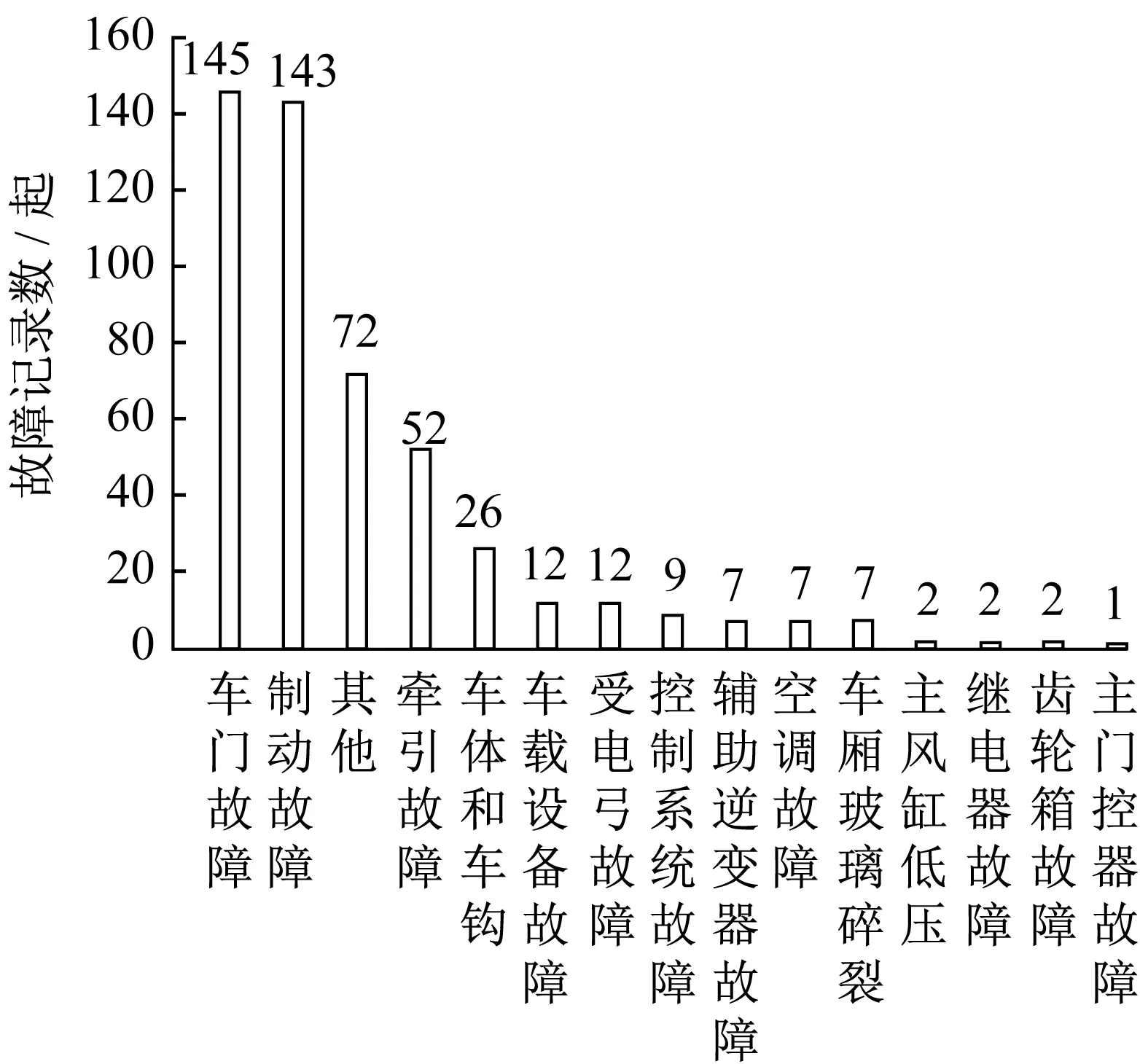
图1 列车故障成因统计Fig.1 Statistics of train fault cause

日均走行公里通常由年总列车运营里程除以年总列车数再除以365d得到，但其忽略了该年新上线列车实际开行天数不到365d的问题，从而导致日均走行公里偏小。本文在计算日均走行公里时对此做了改进，即

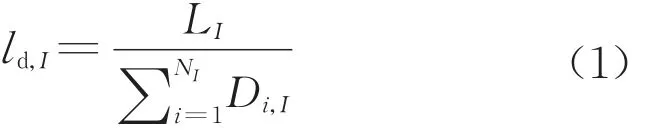
式中：ld，I为列车在第I年日均走行公里，km·d-1；LI为第I年总列车运营里程，km；NI为第I年总列车拥有数，列；Di，I为第i列列车在第I年实际开行天数。

在实现列车累计走行公里的可推算后，以12万km为间隔将其依次划分出多个累计走行公里阶段并确定每个阶段的起止日期。由于列车故障记录的时间范围为2017至2019年，因此只能将起止日期均在2017至2019年内的累计走行公里阶段作为统计对象，对列车在该阶段发生故障的次数进行计数，具体步骤如图2所示。

图2 单列车在各累计走行公里阶段故障发生次数的数据生成Fig.2 Data generation of fault occurrence number for single train in each cumulative running kilometer period

在基础数据的797列对象列车中，有130列因正式投入运营时间较晚未在2017至2019年完成第1个12万km阶段，未被计入数据集。在剩余的对象列车中，分别有271、325、71列在2017至2019年完成了1、2、3个12万km阶段，在数据集中相应地被计入1、2、3次。在基础数据的499起列车故障记录中，有254起的发生日期未在其关联的对象列车于2017至2019年完成任一12万km阶段的起止日期范围内，未被计入数据集。因此，最终生成的数据集中共有1134列对象列车（重复的对象列车因所处累计走行公里阶段不同而具有独立性，故视作一列新的对象列车），245起列车故障记录。各累计走行公里阶段的统计情况如表1所示。

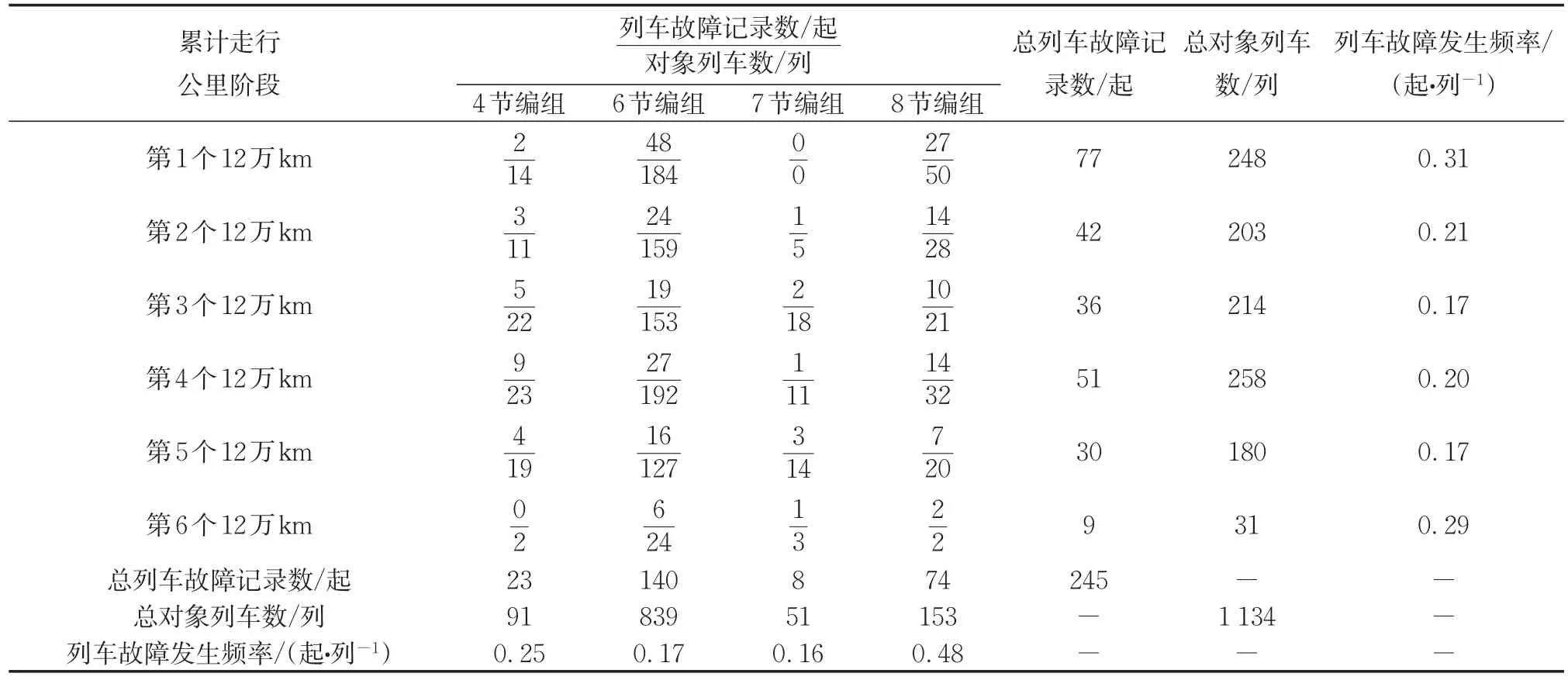
表1 各累计走行公里阶段统计情况Tab.1 Statistics of each cumulative running kilometer period

图3 列车故障发生频率随累计走行公里阶段变化的趋势Fig.3 Trend of train fault frequency with cumulative running kilometer period

从表1可知，随着累计走行公里阶段的推移，列车故障发生频率基本符合先减少再回升的规律，二次抛物线形式较适合描述该影响规律，如图3所示。8节编组的列车故障发生频率最高，但整体来看不同列车编组数的列车故障发生频率之间没有明显的递变规律，这可能是由于4、7节编组的总对象列车数较少导致其频率有一定的异常和不稳定性，从而干扰了变化规律的直观判断。为此采用专门描述定序分类变量间相关程度的Kendall相关系数［16］分析列车编组数与列车故障发生次数之间的影响规律，结果两者的Kendall相关系数为0.13，p值为5.65×10-6小于0.05，由此可认为列车编组数与列车故障发生次数正相关，一定程度上印证了之前关于列车编组数对列车故障发生概率影响的定性分析。

3 列车故障发生概率预测模型

3.1 备选模型

为了从泊松分布、负二项分布、零膨胀泊松分布、零膨胀负二项分布中选择合适的分布构建模型，需观测离散型数据集内不同列车故障发生次数的出现频数，并计算列车故障发生次数总体均值及方差，结果如图4所示。从中可知，列车故障发生次数总体均值与方差十分接近，这符合泊松分布的要求，而列车故障发生0次的数据占比达到81.2%，不能忽视可能存在的零过多现象，故零膨胀泊松分布也值得尝试。因此，选择泊松分布与零膨胀泊松分布构建相应的备选模型。

泊松分布在离散数据分析中相当常用。假定随机变量Y服从泊松分布，则其概率函数如下：

式中：λ为泊松参数，一旦确定即可计算随机变量Y取不同值的概率；y为列车走行一个12万km期间在正线上发生故障的次数。

图4 列车故障发生次数的观测频数Fig.4 Observation frequencies for different train fault occurrence numbers

只要建立泊松参数与列车编组数、列车当前所处累计走行公里阶段的序号之间的回归方程，即可实现考虑各主要影响因素情况下列车故障发生概率的预测。泊松参数与自变量之间的回归通常采用对数线性模型［17］，且累计走行公里阶段推移对列车故障发生概率的影响规律较适合用二次抛物线描述，由此得到模型一如下：

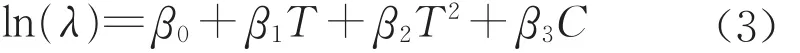
式中：T为列车当前所处累计走行公里阶段的序号，取值为1，2，…，对应第1，2，…个12万km阶段，在架修或大修后需重新累计；C为列车编组数，根据国内常 用 的 编组 形式 ，取 值 一 般 为 4，5，6，7，8；β0，β1，β2，β3为待估系数。

零膨胀泊松分布是在泊松分布的基础上考虑数据集存在零过多现象而提出的分布。假定随机变量Y服从零膨胀泊松分布，则其概率函数如下：

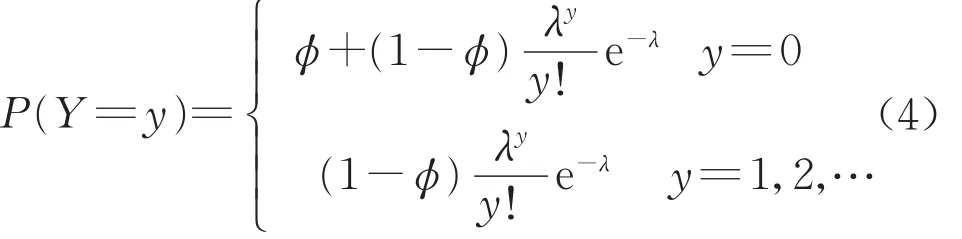
式中：φ为零膨胀参数，表示取值为0的非泊松数据所占的比例。当0＜φ＜1时，数据集存在零过多现象，若φ=0，则式（4）将退化为式（2）。当泊松参数与零膨胀参数都确定后，才可计算随机变量Y取不同值的概率。

泊松参数与零膨胀参数应彼此独立并均与主要影响因素有所关联，为此需对泊松参数、零膨胀泊松参数与列车编组数、列车当前所处累计走行公里阶段的序号进行两两组合来建立回归方程，共有2种可能的组合方案。泊松参数与自变量之间的回归依旧采用对数线性模型，零膨胀参数与自变量之间的回归通常采用logistic回归模型［17］，且累计走行公里阶段推移对列车故障发生概率的影响规律仍用二次抛物线描述，由此得到模型二、模型三，分别如下：

式中：α0，α1，α2为待估系数。

3.2 系数标定

三个备选模型中待估系数的标定基于极大似然估计，通过Gauss-Newton迭代法获得数值解［17］，显著性水平取0.05，具体计算过程由Stata数据分析软件完成。

各备选模型的估计结果如表2所示，各模型中变量C的系数均反映了列车编组数的增加会提高列车故障发生概率，变量T和T2的系数均反映了累计走行公里的增加会使列车故障发生概率先降低后回升。其中，模型一中所有变量均通过显著性检验，模型成立；模型二中泊松参数与零膨胀参数的常数项未通过显著性检验，在经过各种可能的尝试后，发现剔除泊松参数的常数项可使剩余变量均通过显著性检验，由此得到改进后的模型二；模型三中零膨胀参数的变量均未通过显著性检验，在经过各种可能的尝试后，发现模型三始终无法成立，故在后续模型比选时不再考虑。

表2 模型估计结果Tab.2 Estimated results of alternative models

3.3 模型比选

针对模型一和模型二，从两方面定量比较两者的优劣。首先，比较两个模型所预测的不同累计走行公里阶段总列车故障记录数与实际值的平均差异程度δ，计算方法见式（7）。该数值越低说明模型预测效果越好，具体结果见表3。

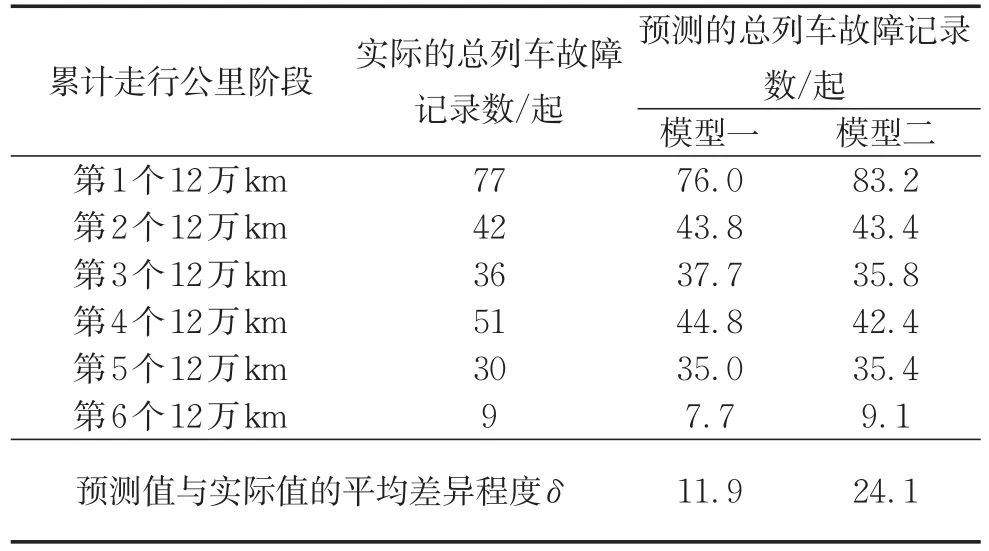
表3 各累计走行公里阶段总列车故障记录数的预测结果Tab.3 Predicted results of total train fault records in each cumulative running kilometer period

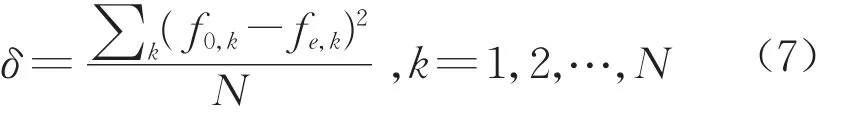
式中：f0，k为第k个阶段实际的总列车故障记录数；fe，k为第k个阶段预测的总列车故障记录数；N为阶段个数。

其次，绘制ROC曲线比较两个模型的泛化能力，ROC曲线下包含的面积越大，模型泛化性能越好［8］。需要注意的是，ROC曲线的适用范围是二分类问题，而两个模型中列车故障发生次数存在0、1、2、3起的类别，属于多分类问题，所以需要进行二分类的转化：列车未发生故障（0起）、列车发生了故障（1起以上）。绘制得到的ROC曲线如图5所示。

从比较结果来看，模型一无论是预测效果还是泛化能力均优于模型二。因此，最终的城市轨道交通正线列车故障发生概率预测模型如下：

图5 各备选模型的ROC曲线Fig.5 ROC curves for each alternative model

确定泊松参数后，便可通过1-P(Y=0)得到列车故障发生概率。不同列车编组数、累计走行公里阶段组合下的列车故障发生概率如表4所示。通过比较列车故障发生概率在横向、纵向的增长情况可知，在城市轨道交通列车处于第6个12万km阶段之前，相比于累计走行公里阶段的推移，列车编组数的增加对列车故障发生概率的影响更大。这可能是因为整列车可视为由多节车厢组成的串联系统，车厢数越多整列车的可靠性越低，而每节车厢的可靠性只有在达到一定使用程度后才会发生大的变化，从而导致了很长一段时间内整列车的故障发生概率更容易受列车编组数的影响。

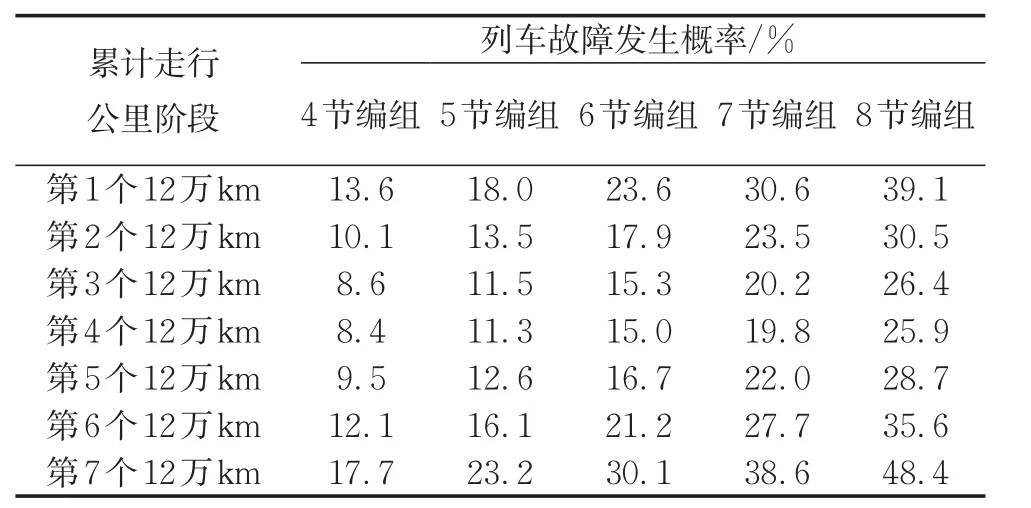
表4 不同影响因素组合下的列车故障发生概率Tab.4 Train fault probabilities corresponding to different combinations of influencing factors

4 结论

以城市轨道交通列车为研究主体，综合考虑多方因素，提出了基于泊松分布的城市轨道交通正线列车故障发生概率预测模型。主要研究工作总结如下：

（1）通过定性分析得到列车编组数、累计走行公里、架修或大修经历为列车故障发生概率的主要影响因素。当列车经历架修或大修后，需重新累计其走行公里。

（2）探究了各影响因素对列车故障发生概率的影响规律：列车编组数的增加会提高列车故障发生概率；累计走行公里的增加会使列车故障发生概率先降低后回升。

（3）以每12万km为观测范围生成单列车在一定走行公里内故障发生次数的离散数据集，基于数据呈现的分布特征选择泊松分布、零膨胀泊松分布构建了3个备选模型。之后根据显著性检验、预测值与实际值的平均差异程度以及ROC曲线进行模型比选，结果显示基于泊松分布的模型最优。由此提出了基于泊松分布的城市轨道交通正线列车故障发生概率预测模型。

（4）根据模型结果可推断：在列车编组数固定的情况下，列车故障发生概率会在列车投入运营后的第4个12万km阶段达到最低值，在第7个12万km阶段超过初始值。