基于高斯伪谱法的汽车弯道超车路径规划与跟踪控制

张家旭 ，周时莹，赵 健，施正堂

(1. 吉林大学汽车仿真与控制国家重点实验室，长春 130022；2. 中国第一汽车集团有限公司智能网联研发院，长春 130011；3. 浙江亚太机电股份有限公司智能汽车控制系统研究院，杭州 311200)

全国汽车保有量持续增加产生的交通拥堵和交通安全问题推动着无人驾驶技术加速发展，而汽车换道路径规划与跟踪控制是无人驾驶技术安全可靠应用的重要基础[1-2]．因此，国内外众多企业和学者对无人驾驶技术涉及的汽车换道路径规划与跟踪控制展开了深入的研究，并取得了较丰富的研究成果．

文献[3]针对静止的障碍物，采用几何方法规划出了一条汽车换道避障轨迹作为参考轨迹，并以最小化参考轨迹偏离误差作为优化目标，将汽车换道避障轨迹规划问题转化为最优化问题，通过梯度下降法求解此最优化问题得到可执行的汽车换道避障轨迹．同时，将离散化的汽车运动学方程作为预测模型，采用模型预测控制方法设计了汽车换道避障轨迹跟踪控制策略，实现目标轨迹的跟踪控制．文献[4]综合考虑了汽车换道避障过程的安全性、舒适性和可行性约束，基于7 次多项式曲线将汽车换道避障问题转化为约束最优化问题，并利用具有全局搜索能力的遗传算法求解此约束最优化问题得到满足安全性、舒适性和可行性约束的汽车换道避障目标路径．为了使汽车可以快速、准确和稳定地跟踪汽车换道避障目标路径，文献[4]充分考虑了主动前轮转向系统的动态特性，采用μ 综合方法设计了汽车换道避障路径跟踪控制策略．文献[5]针对极限工况下汽车换道避让静止障碍物的路径规划与跟踪控制问题，采用正切函数规划汽车换道避障路径，并采用修正的哈密顿方法设计主动制动和主动转向的集成控制策略，实现汽车换道避障路径的跟踪控制．文献[6]以高斯分布为基础规划出了符合驾驶员操纵特性的汽车换道避障路径，并采用反馈线性化方法设计了汽车换道避障路径跟踪控制策略，实现汽车换道避障路径的跟踪控制．上述研究成果未考虑运动障碍物对汽车换道路径规划与跟踪控制的影响．

为此，文献[7]以三角函数和指数函数为基础，建立了道路边界和运动障碍物的人工斥力场，以及目标点的人工引力场，并且将二者合成场的最速下降方向构成的路径作为汽车换道避障目标路径．随后，将离散化的汽车运动学方程和汽车动力学方程作为预测模型，采用模型预测控制方法设计了汽车换道避障路径跟踪控制策略，实现目标路径的跟踪控制．文献[8]以S 型函数为基础，利用滚动优化思想规划出了避让运动障碍物的汽车换道路径，并采用模型预测控制方法设计了汽车换道避障路径跟踪控制策略，通过控制前轮转向角来实现目标路径的跟踪控制．文献[9]基于6 次多项式曲线规划出了汽车换道路径，引导汽车避让运动障碍物．同时，采用模型预测控制方法设计了主动前轮转向系统和直接横摆力矩系统的集成控制策略，实现规划路径的跟踪控制．文献[10]基于人工势能精细化阻力方法提出了一种汽车换道避障路径规划算法，以及基于模型预测控制方法提出了一种汽车换道避障路径跟踪控制策略，并通过仿真分析证明了研究结果可使汽车安全、舒适、高效地避让运动障碍物．上述研究成果虽然考虑了运动障碍物对汽车换道路径规划与跟踪控制的影响，但未考虑路径曲率对汽车换道路径规划与跟踪控制的影响．

弯道超车场景是无人驾驶技术应用场景的重要组成部分，当前方低速行驶汽车由于自身原因已严重影响弯道车流速度且旁边存在安全行驶车道时，无人驾驶汽车规划和跟踪可行的路径，实现弯道超车．鉴于此，本文综合考虑前方低速行驶汽车等运动障碍物和路径曲率对汽车换道路径规划与跟踪控制的影响，提出一种基于高斯伪谱法的汽车弯道超车路径规划算法，以及基于干扰观测器的汽车弯道超车路径跟踪控制策略．首先，基于本车和前方低速行驶汽车的运动学方程将汽车弯道超车路径规划问题描述为约束最优化问题，并采用高斯伪谱法将其转化为非线性规划问题进行求解，从而得到满足相对运动方程、过程和边界约束的汽车弯道超车路径．随后，以汽车后轴中点横向坐标作为非时间参考量，基于汽车运动学方程建立包含复合干扰的非时间参考名义模型，并利用径向基神经网络对未知非线性函数的无限逼近能力设计干扰观测器，在线估计和前馈补偿名义模型包含的复合干扰，同时基于李雅普诺夫稳定理论推导出具有一致最终有界特征的汽车弯道超车路径跟踪控制策略，实现对基于高斯伪谱法规划出的汽车弯道超车路径的跟踪控制．最后，基于车辆动力学软件构建模型在环仿真系统，验证所提出的汽车弯道超车路径规划算法与跟踪控制策略的可行性和有效性．

1 汽车弯道超车路径规划

1.1 汽车弯道超车路径规划问题描述

汽车弯道超车路径用于引导汽车在两个转向相同、半径不同的圆曲线之间平滑切换，以使汽车安全、舒适地跨越前面同方向低速行驶的汽车．如图1所示，建立固定坐标系Oxy，选取本车后轴中点作为参考点，假设本车初始时刻 t0的方位角为 θ0，路径曲率为，后轴中点坐标为，则其运动学方程可描述为

式中：vH为本车车速；(xH,yH)、θH、ρH和 kH分别为本车几何中心点坐标、本车方位角、路径曲率和路径曲率变化率．

图1 汽车弯道超车路径Fig.1 Path for corner overtaking of vehicle

如图1 所示，假设本车前面同方向低速行驶的汽车车速和路径曲率保持不变，分别为vG和，若其初始时刻 t0的方位角为θ1，则其初始时刻 t0的后轴中点坐标为，由此可得其运动学方程为

式中：( xG,yG)和 θG分别为前面同方向低速行驶的汽车几何中心点坐标和方位角．

联合式(1)描述的本车运动学方程和式(2)描述的前面同方向低速行驶汽车运动学方程，可建立描述本车与前面同方向低速行驶汽车相对运动的方程为

式中：u = kH为相对运动方程的控制量，初始时刻 t0的值 为零；为相对运动方程的状态量，初始时刻 t0的值为

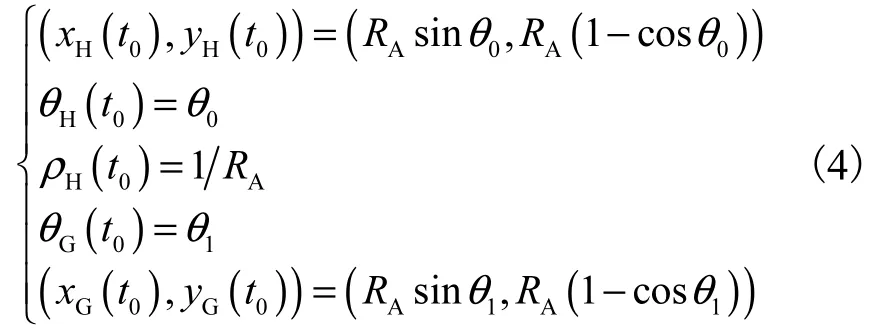
为了保持本车弯道超车过程中的操纵特性处于线性工作区域，对其侧向加速度有如下约束

式中aymax为汽车弯道超车过程的最大侧向加速度．

由式(5)可得本车路径曲率约束条件为

假设本车弯道超车过程中的车速保持不变，对式(5)求一阶导数，可得

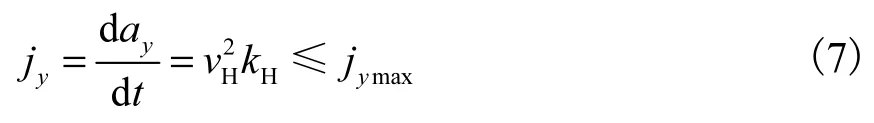
式中jymax为汽车弯道超车过程的最大侧向加速度.

由式(7)可得本车路径曲率变化率约束条件为

如图1 所示，本车在弯道超车结束后应沿着原车道稳定行驶，由此可得本车在弯道超车过程结束时刻tf须满足如下约束条件．

考虑本车弯道超车过程的车道边界约束条件，可得

式中 σ1＞0 为车道边界余量．

考虑本车与前面同方向低速行驶汽车的安全距离约束条件，可得

式中：Wd为车道宽度；σ2＞0 为安全距离余量．

以最小化汽车弯道超车路径弧长为优化目标，将上述汽车弯道超车路径规划问题转化为如下的最优化问题．

1.2 汽车弯道超车路径规划问题求解

本节基于高斯伪谱法将式(12)描述的汽车弯道超车路径规划问题转化为非线性规划问题进行求解．为此，将汽车弯道超车路径规划问题的时间区间归一化为

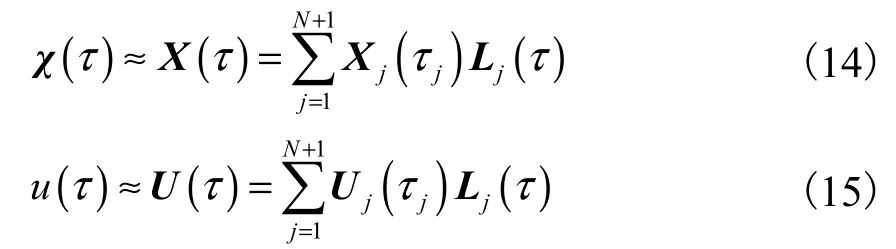
利用式(14)和式(15)将式(12)描述的汽车弯道超车路径规划问题转化为如下的非线性规划问题．

式中Dij为微分近似矩阵，可表示[12]为

采用成熟的求解器求解式(16)描述的非线性规划问题[13]，即可得到满足相对运动方程、过程和边界约束的汽车弯道超车路径．

2 汽车弯道超车路径跟踪控制

汽车弯道超车路径跟踪控制的任务是实时计算前轮转向角控制指令，使汽车快速、准确和稳定的跟踪基于高斯伪谱法规划出的目标路径．由于汽车弯道超车过程中的操纵特性处于线性工作区域，可以采用汽车运动学方程近似描述汽车弯道超车过程的行驶状态[14]．

式中：δH为汽车前轮转向角；L 为汽车轴距；Δ 为未建模动态和外界扰动引起的系统加性不确定性．

为了简化基于式(18)设计汽车弯道超车路径跟踪控制系统的过程，采用汽车后轴中点横向坐标作为非时间参考量，已知目标路径点的纵向坐标值和方位角分别为 yr和 θr，定义新的状态量为和，则式(18)描述的汽车运动学方程可简化为

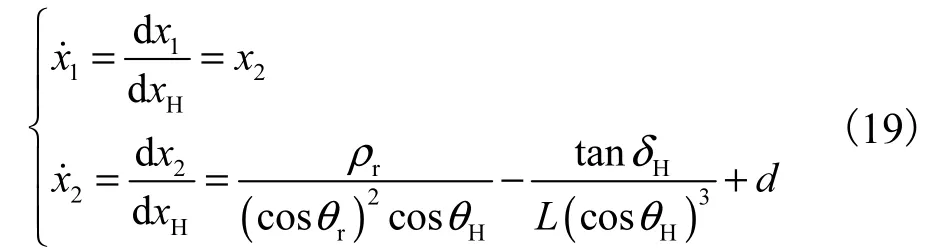
为了抑制式(19)包含的系统复合干扰对汽车弯道超车路径跟踪控制系统性能的影响，采用径向基神经网络设计干扰观测器，对其进行在线估计和前馈补偿．利用径向基神经网络的结构特征将式(19)包含的系统复合干扰表示为

式中：W∗为径向基神经网络的未知最优权重向量；ς 为径向基神经网络的满足边界约束的最小估计误差；φ (x)为径向基神经网络的高斯基函数向量，其第i 个元素可表示为

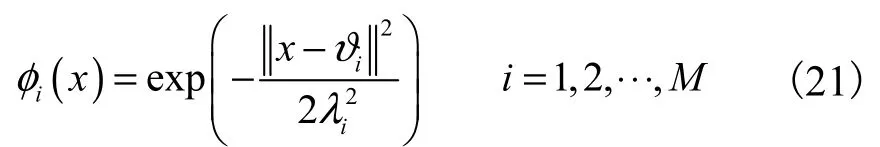
式中： ϑi和λi为高斯基函数向量中第i 个元素的中心和宽度；M 为高斯基函数向量包含的元素数量．

针对式(20)包含的径向基神经网络的未知最优权重向量，采用李雅普诺夫稳定性理论设计未知最优权重向量自适应律和汽车弯道超车路径跟踪控制律，由此得到如下定理．

定理针对式(19)描述的汽车运动学方程，设计如下汽车弯道超车路径跟踪控制律

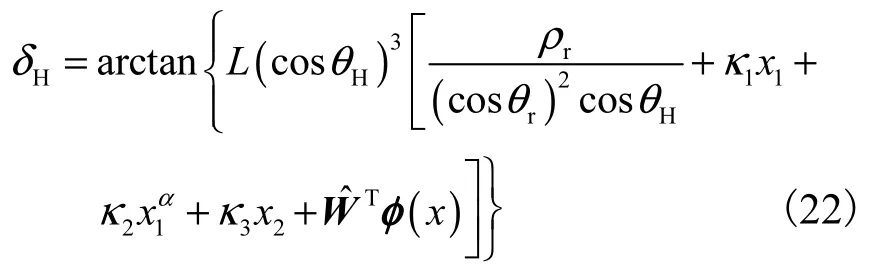
式中：κ1＞0 、κ2＞0 、κ3＞0 和奇数α ＞1 分别为汽车弯道超车路径跟踪控制律的设计参数；为径向基神经网络的未知最优权重向量估计，其自适应律为

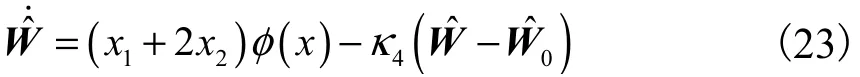
式中：κ4＞0 为未知最优权重向量自适应律的设计参数；为未知最优权重向量的初始估计．若设计参数满足

则汽车弯道超车路径跟踪控制闭环系统的状态轨迹是一致最终有界的．

证明将式(22)描述的汽车弯道超车路径跟踪控制律代入式(19)描述的汽车运动学方程，可得

针对式(26)描述的系统，定义李雅普诺夫候选函数为

对式(27)求导，可得

将式(23)和式(26)代入式(28)，可得

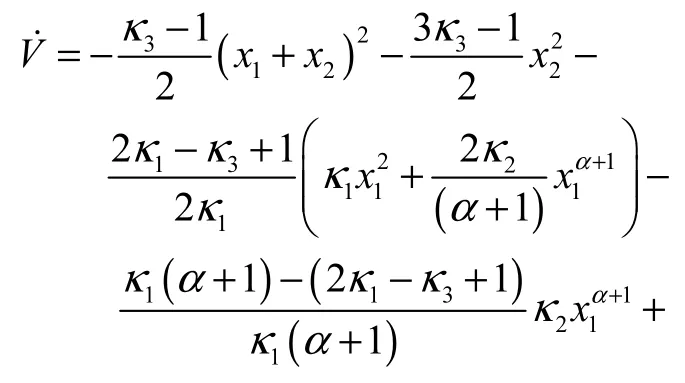
由杨氏不等式[15]，可得

将不等式(30)～(32)代入式(29)，可得

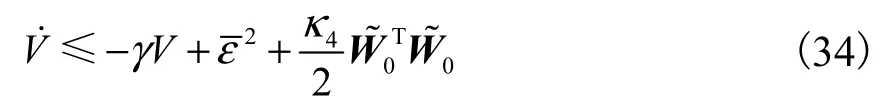
由式(34)可得

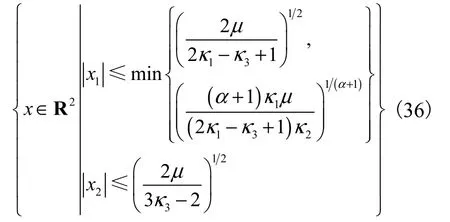
由式(36)可知：基于径向基神经网络设计的干扰观测器可有效提高汽车弯道超车路径的跟踪精度．

3 仿真结果及分析

本节采用m 语言实现汽车弯道超车路径规划算法，离线规划出汽车弯道超车路径，并在 Matlab/Simulink 环境下将汽车弯道超车路径规划算法的输出无缝连接到基于车辆动力学软件CarSim 构建的模型在环仿真系统，验证汽车弯道超车路径跟踪控制策略的可行性和有效性．在仿真验证过程中，本车初始车速设置为20 m/s，前方低速行驶汽车车速设置为10 m/s，路径内圆半径设置为400 m，路径外圆半径设置为403.75 m，汽车弯道超车路径规划与跟踪控制参数设置如表1 所示，包含干扰观测器的汽车弯道超车路径跟踪控制策略与不含干扰观测器的汽车弯道超车路径跟踪控制策略的仿真对比结果如图2 和图3所示．

表1 汽车弯道超车路径规划与跟踪控制参数Tab.1 Path planning and tracking control parameters for corner overtaking of vehicle

如图2 所示，本文所提出的汽车弯道超车路径规划算法与跟踪控制策略可以引导本车在两个转向相同、半径不同的圆曲线之间平滑切换，进行使本车安全、舒适地跨越前方低速行驶的汽车．如图3 所示，包含干扰观测器的汽车弯道超车路径跟踪控制策略与不含干扰观测器的汽车弯道超车路径跟踪控制策略均可以稳定地跟踪汽车目标路径和目标方位角.同时，相对于不含干扰观测器的汽车弯道超车路径跟踪控制策略，包含干扰观测器的汽车弯道超车路径跟踪控制策略对汽车目标路径和目标方位角的跟踪精度更高，尤其在汽车由外圆路径驶回内圆路径过程中(图3 中6～8 s 时间区间)，包含干扰观测器的汽车弯道超车路径跟踪控制策略可以使汽车更加平顺稳定地跟踪目标路径和目标方位角．

图2 不同时刻本车和前方低速行驶汽车相对位置Fig.2 Relative positions of the host vehicle and low-speed vehicle in front of it at different times

图3 汽车弯道超车过程的行驶状态Fig.3 Status of vehicle in the corner overtaking process

4 结 论

(1) 基于本车和前方低速行驶汽车的运动学方程将汽车弯道超车路径规划问题描述为约束最优化问题，并采用高斯伪谱法将其转化为非线性规划问题进行求解，得到满足相对运动方程、过程和边界约束的汽车弯道超车路径．

(2) 基于汽车运动学方程建立包含复合干扰的非时间参考名义模型，采用径向基神经网络设计干扰观测器来估计和补偿名义模型包含的复合干扰，并采用李雅普诺夫稳定理论推导出汽车弯道超车路径跟踪控制策略，实现对汽车弯道超车路径的快速、准确和稳定的跟踪控制．

(3) 在Matlab/Simulink 环境下构建模型在环仿真系统，验证所提出的汽车弯道超车路径规划算法与跟踪控制策略的可行性和有效性，结果表明：所提出的汽车弯道超车路径规划算法与跟踪控制策略可以引导本车在两个转向相同、半径不同的圆曲线之间平滑切换，使本车安全、舒适地超越前方低速行驶的汽车．