基于VMD-LSSVM 的水下滑翔机深平均流预测

何柏岩，杜金辉，杨绍琼, ，张润锋，牛文栋, ，兰世泉

(1. 天津大学机械工程学院，天津 300350；2. 天津大学青岛海洋技术研究院，青岛 266237；3. 青岛海洋科学与技术试点国家实验室，海洋观测与探测联合实验室，青岛 266237)

水下滑翔机(underwater glider)是一种新型水下无人航行器．相对于其他水下航行器，水下滑翔机兼具低成本、长续航、易维护、航行范围广的特点[1]．水下滑翔机易于集成多种不同传感器，进行压力、温度、电导率、叶绿素、溶解氧、湍流等不同变量的测量[1-2]．随着对海洋探索的深入，以水下滑翔机为纽带的海洋探测与实验越来越广泛，水下滑翔机被应用于诸如中尺度涡[1,3]、亚中尺度涡等[4]海洋现象的研究和极端环境、突发危机事件的调查中[5]．水下滑翔机迅速在海洋科学研究中占据一席之地．

水下滑翔机仅通过改变浮力和姿态实现上浮下潜运动的原理，运动速度较小；它浮出水面时与卫星通信，来确定位置信息，在水下时无法与卫星通信定位，因而它在水下的位置通过航位推算来确定．但由于洋流的影响，水下滑翔机的运动会发生漂移，导致推算航位与实际位置会存在偏差[6]．Merckelbach等[7]提出了深平均流的概念，即用水下滑翔机理论出水位置和真实出水位置的矢量差除以剖面运行时间得到深平均流．深平均流将水下滑翔机自身的影响和外部环境的影响综合到一起，被广泛应用于航位推算、路径规划中．Smith 等[8]将深平均流结合区域海洋动力学模型，对Slocum 水下滑翔机进行航点设定来预规划其航线，对航行误差的计算表明，这种方法的导航精度更高．Chang 等[9]结合南卡罗来纳州长湾的区域海洋模型，把水下滑翔机最新的海洋观测信息作为反馈进行海洋模型动态调整，并基于此进行动态路径规划．Zhou 等[10]将深平均流按照剖面运行的时间顺序排列构成时间序列，结合经验模态分解和机器学习的方法预测深平均流，进而进行局部流场重构和路径规划．Zhang 等[11]基于3 台“海燕”水下滑翔机的观测数据，利用经验贝叶斯克里金法来进行空间插值来构造深平均流场．

目前我国尚无较为准确的海洋模型，无法即时输入外部信息给正在运行的水下滑翔机；其次，水下滑翔机的体积有限，限制了可携带电池容量．为了实现长续航要求，必须进行严格的能耗管理[12-13]．洋流流速传感器并非水下滑翔机的标准配置传感器，因此在非特定搭载流速传感器的任务中，水下滑翔机无法测量所处环境的洋流流速．

而在机器学习的训练及预测中，水下滑翔机完成新的剖面后，将最新的深平均流数据加入到训练集的剖面时间序列中，可以构成新的深平均流序列，来动态地预测后一个或几个剖面．但是，预测的准确度受到序列尾部数据的影响较大．因此，考虑到经验模态分解的弊端，尤其是端点效应的影响[14]，分解后的预测相对于原序列直接预测的精度并非一定有所提升，即在海洋环境趋于恶劣的情况下，水下滑翔机偏离预设航线的程度会加剧且变化程度加剧，深平均流计算数值较先前剖面的数值会更大．因此在构成深平均流序列时最新的数据，即序列尾部数据会出现较大幅度的振荡，进行实时经验模态分解时便会出现端点效应，很大程度上影响预测精度．

为了降低端点效应的影响，提高预测精度，本文提出了实时的基于变分模态分解(VMD)和最小二乘支持向量机(LSSVM)的水下滑翔机深平均流预测．首先，构建水下滑翔机动态深平均流精简模型，通过与航位推算深平均流对比得知简化模型的合理性；其次，把深平均流数据按照剖面前后时间排列成序列，把得到每一剖面的最新深平均流数据累加到序列中构成最新序列，对其进行 VMD 处理，利用LSSVM 对各分量分别预测后叠加得到深平均流预测结果．通过海试试验验证了本文所提方法的有效性．

1 水下滑翔机深平均流计算模型

水下滑翔机的运动周期可以分为如下几步：

(1) 下潜前的海面等待阶段，此时可通过GPS获得水下滑翔机的经纬度信息以及历史剖面的部分运行信息；

(2) 收到下潜指令，调节油囊油量和电池包位置，减小浮力，并使重心前移，开始低头下潜，并断开GPS 连接；

(3)达到预定深度之前，调节油囊油量和电池包位置，增大浮力，重心后移，水下滑翔机上浮；

(4)浮出海面，完成本剖面运动．

水下滑翔机的运动周期中绝大部分时间处于断开连接状态，无法获得其航行信息，而是通过航位推算获取位置信息．而由于洋流的影响，水下滑翔机的实际出水位置往往会偏离理论出水位置．设第n 个剖面的理论出水位置为 Pntheory，实际出水位置为 Pnactual，Pntheory与Pnactual之间的距离为L，该剖面运行时间为nT ，则该剖面水下滑翔机的深平均流为

深平均流能影响水下滑翔机的运动．水下滑翔机的理论出水位置可在浮出海面后通过GPS 信息得到，而理论出水位置的计算可以通过航位推算方式得到：假设航位推算的周期为 Δt ，k 为一个剖面内的采样次数，根据CTD 传感器得到的水下滑翔机深度方向的速度为 vy，滑翔角为γ，攻角为α ，则水下滑翔机第 n+ 1个剖面的理论出水位置 Pn+1theory为

其中

这种航位推算需要利用温盐深传感器在整个剖面周期的数据进行计算，并且在浮沉切换过程中，会出现很多滑翔角γ 接近0 的数据，因此计算的相应水平位移过大，甚至能影响整个剖面的结果．并且为了节约能耗，航位推算所得数据只能在回收水下滑翔机后才能下载得到，无法及时通过GPS 传回给岸基控制台，因此不利于实时调整．

基于此，本文采用水下滑翔机浮出海面时所传回的信息数据，建立短数据精简深平均流计算模型，在接收下潜指令前完成深平均流的计算及预测，以保证顺利完成航向修正，即

式中：ΔnL 为第n 个剖面的航行距离； Dn为第n 个剖面的运行深度；γ1、γ2分别为下潜、上浮时的滑翔角．图1(a)、(b)分别为经度方向和纬度方向的短数据精简深平均流和航位推算深平均流结果的对比．

图1 2种深平均流结果对比Fig.1 Comparison of the results of the two types of DACV

评价指标为均方根误差RMSE 及2 种方法的相关性系数 r ( vdav,vdavDR)．均方根误差和相关性系数的公式分别为

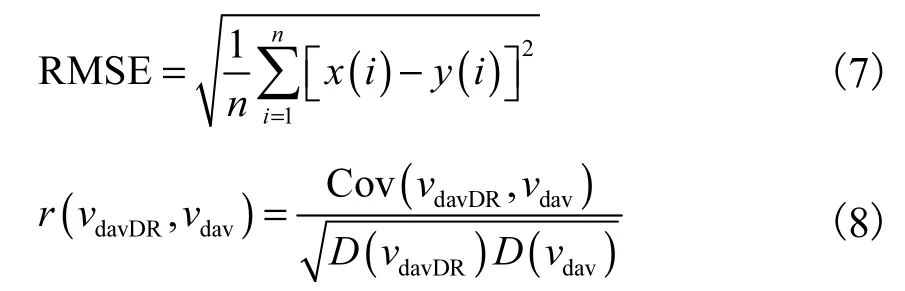
式中：vdav为本文所提方法的深平均流；vdavDR为航位推算所得的深平均流；C ov( vdav,vdavDR)为二者的协方差；D ( vdav)、D ( vdavDR)分别为二者的方差．

经度、纬度方向2 种计算方法的均方根误差分别为0.028 9 和0.032 1，相关系数分别为0.937 1 和0.930 2．考虑到水下滑翔机运动过程中攻角的变化及浮沉切换的振荡阶段会对航位推算结果造成一定的误差，因此，在基于岸基准实时控制调整的要求下，利用短数据精简深平均流来代替航位推算深平均流的计算方法是合理的．

将累计剖面的深平均流数据依次排列组成时间序列，可预测后续时段海流，进而对水下滑翔机航向修正．

2 最小二乘支持向量机

支持向量机[15]是一种基于统计理论的机器学习方法，能很好地处理小样本数据以及高维数据，对学习模型的泛化能力强，因此在机器学习领域应用广泛，尤其适合处理高维度、小样本及非线性的问题，但其训练训练过程非常复杂．Suykens 等[16]在支持向量机中引入最小二乘线性系统，提出最小二乘支持向量机(LSSVM)模型，利用等式进行约束，提高计算效率[17]．

假设k 个输入样本数据 xi对应的输出分别为yi= ( i = 1,2, …, k )，其中 xi∈Rn的维度为n，yi∈R 为第i 个输入对应的输出值．利用非线性高维映射函数φ (⋅)将输入样本数据映射到高维特征空间Q 中，使原空间无法线性可分的问题转化为高维空间中线性可分的问题，即在高维空间Q 中样本输入输出进行拟合

式中：ω 为权值向量；b 为偏置向量．根据结构风险最小化原理建立等式优化目标函数

式中：c 为正则化因子；ξ 为松弛变量．c 值越高越容易过拟合，反之则容易欠拟合．因此合理的c 能提高模型的泛化能力．

设拉格朗日乘子为 ai( i = 1,2, …, k )，通过拉格朗日乘数法进行求解，得到方程组

得到方程组

式中Ω 为核函数，

本文采用高斯核函数，利用十折交叉验证法求解高斯核函数的参数．则

求解出a 和b 后，得到LSSVM 回归函数为

3 变分模态分解

VMD 是一种自适应、完全非递归的信号分解方法[18]．根据预设的模态数，它将信号分解为具有不同中心频率的有限带宽，通过采用交替方向乘子法，不断更新各模态及其中心频率，逐步将各模态解调到相应的基频带，并将各个模态及其相应的中心频率提取出来，最终得到了各个具有不同中心频率的分量．

变分模态分解本质是创造并求解变分问题，过程如下[18]．

(1) 计算各模态带宽，利用Hilbert 变换计算每个模态函数的解析信号，进而获得其单侧频谱

(2) 对每个模态函数所对应的中心频率的指数项进行混叠，调制各模态的频谱到基频带

(3) 解调．根据高斯平滑度和梯度平方准则，计算梯度的平方L2 范数，得到各个模态的带宽．变分目标函数为

(4) 引入二次惩罚项α 和拉格朗日乘子λ 来求解目标函数，得到增广拉格朗日函数

式中〈⋅〉表示内积运算．

中心频率更新表达式为

4 基于VMD-LSSVM的深平均流预测

4.1 预测流程

深平均流的大小反映了水下滑翔机在洋流影响下偏离预设方向的程度．本文以天津大学“海燕-L”长航程水下滑翔机为平台，一般其单剖面运行周期4～5 h，最大工作深度为1 000 m，基于历史航行数据进行深平均流建模并预测．预测流程如下：

(1) 利用水下滑翔机浮出水面后的通信短数据，进行经度、纬度方向短数据精简深平均流计算，前后排列构成时间序列；

(2) 利用VMD 对深平均流时间序列进行分解，得到若干相对平稳的分量．通过分解验证，本文将序列分解为5 组模态和一组残差序列；

(3) 在预测前，对数据进行归一化，使数据分布于[ 0,1] ．假设序列数据的最大值为 vmax，最小值为vmin，则归一化后的数据为

(4) 对各分量单独预测，预测结果叠加，得到最终的归一化后的深平均流预测值，并将其反归一化，得到实际的下一剖面的深平均流预测值为

由于水下滑翔机的单剖面航程相较所处海洋区域很小，假设局部区域内流场变化恒定，不考虑空间变化，深平均流只与其历史剖面的数据有关，即

式中k 为相关的剖面个数．若k 过大，表示当前剖面深平均流与过早的深平均流数据相关，则会使模型不够准确；若k 过小，则模型只会考虑临近当前剖面的深平均流数据，不能很好地涵盖全部相关信息．因此，考虑到“海燕-L”水下滑翔机单剖面的时间为4～5 h，本文选择 k = 2,3,4,5，将深平均流数据分解到经度和纬度方向分别进行计算．

4.2 海试验证

团队于2019 年8 月在南海北部区域进行“海燕-L”水下滑翔机海试试验．本节利用“海燕-L”某航段205 个剖面进行验证．“海燕-L”水下滑翔机的布放场景如图2 所示．“海燕-L”水下滑翔机本次试验的海上轨迹如图3 所示．

图2 “海燕-L”水下滑翔机布放Fig.2 Setting of the“Petrel-L” underwater glider

图3 “海燕-L”水下滑翔机航迹Fig.3 Trajectory of the“Petrel-L” underwater glider

本文通过对“海燕-L”进行连续动态深平均流预测，来验证所提方法的可行性．将VMD-LSSVM 的结果与未经分解的深平均流预测结果(Orig-LSSVM)和经EMD 的深平均流预测结果(EMD-LSSVM)，以及基于 LSTM 的 3 种方法(Orig-LSTM、EMDLSTM、VMD-LSTM)对比．k 是计算时输入剖面的个数，每种方法都能在k ＋1 个剖面时得到结果．为了便于对比k 不同取值时的结果，所有的方法都从第6 个剖面开始计算．正值分别为东向、北向，负值为西向、南向．深平均流预测的数值评价指标为均方根误差RMSE、最大预测误差及预测值与实际值的相关性系数

图4 分别为 k = 2,3,4,5时基于LSSVM 的经度方向深平均流预测结果，图5 为k＝2，3，4，5 时基于LSSVM 的纬度方向的深平均流预测结果．表1、表2分别为 k = 2,3,4,5时深平均流在经度、纬度方向的6种不同方法的预测结果．

图4 基于LSSVM的经度方向深平均流预测结果Fig.4 Prediction results of DACV in the longitudinal direction based on LSSVM

图5 基于LSSVM的纬度方向深平均流预测结果Fig.5 Prediction results of DACV in the latitudinal direction based on LSSVM

4.3 结果分析

由图6、图7以及表1、表2 可知，基于LSSVM的深平均流预测方法能对深平均流进行有效预测．

表1 经度方向预测结果Tab.1 Prediction results in the longitudinal direction

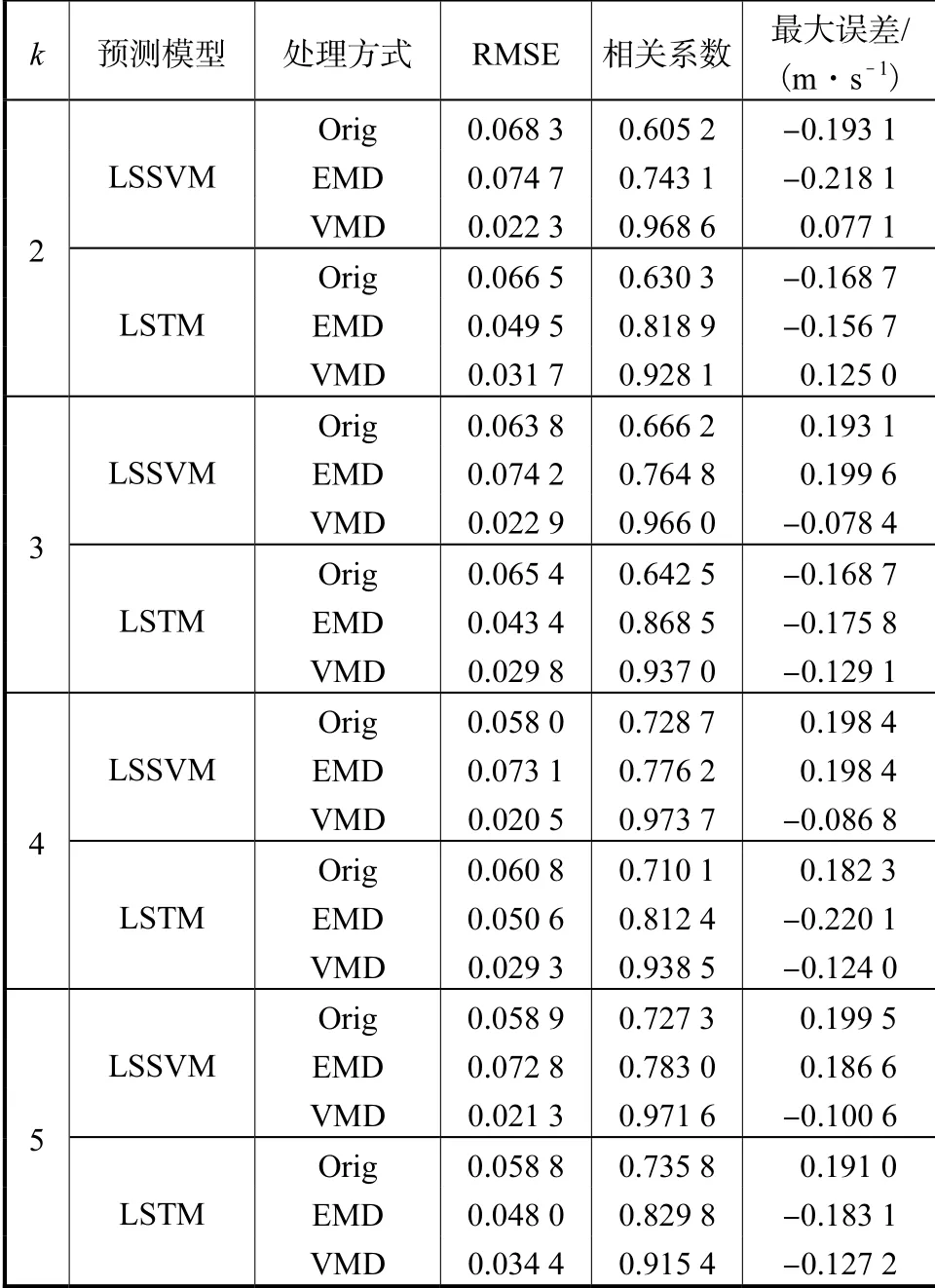
表2 纬度方向预测结果Tab.2 Prediction results in the latitudinal direction

在经度和纬度方向上，得到最优结果的方法k 值都为4．这表明以前4 个剖面的深平均流作为输入，来预测第5 个剖面的深平均流最为准确．

Orig-LSSVM 预测的均方根误差当k =4 时最小，在经度和纬度方向分别为0.061 4 和0.058 0．预测在整个序列内都表现出较差的结果，无法很好地捕捉到深平均流的变化．

EMD-LSSVM 在深平均流较小或变化较为规律的情况下表现出较好的预测效果，但当深平均流增大或变化较不稳定时，EMD-LSSVM 的预测结果变得不稳定，即便仍能保持变化趋势，但预测的数值结果出现较大失真．以k =4 经度和纬度方向的预测为例，如图6 和图7 所示．

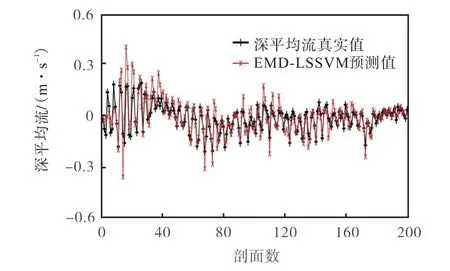
图6 k＝4时EMD-LSSVM的经度方向深平均流预测结果Fig.6 Prediction results of EMD-LSSVM in the longitudinal direction of DACV when k＝4

图7 k＝4 时EMD-LSSVM的纬度方向深平均流预测结果Fig.7 Prediction results of EMD-LSSVM in the latitudinal direction of DACV when k＝4

这种情况下，EMD-LSSVM 预测会出现个别很大的误差，使得整体预测效果变差，全序列的均方根误差甚至要高于不分解的 LSSVM 预测(Orig-LSSVM)，最大误差比Orig-LSSVM 更大．以k =4 时为例，预测误差如图8 和图9 所示．

VMD-LSSVM 的预测结果在数值大小和变化趋势上与真实结果最为接近，无论k 的取值为何，都体现了出众的泛化能力，且在k =4 时，深平均流预测结果最优：在经度和纬度方向，均方根误差分别为0.025 7 和0.020 5；预测结果与真实结果的相关性最大，相关系数分别为0.948 4 和0.973 7．

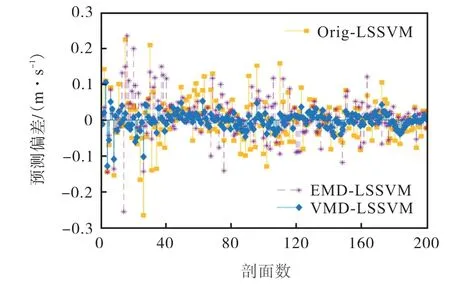
图8 k＝4时LSSVM的经度方向深平均流预测偏差Fig.8 Prediction error of LSSVM in the longitudenal direction of DACV when k＝4

图9 k＝4时LSSVM的纬度方向深平均流预测偏差Fig.9 Prediction error of LSSVM in the latitudinal direction of DACV when k＝4

由表1、表2 中数据可知，基于LSTM 的方法同样能对深平均流进行预测，并且对原序列数据进行VMD 分解后，预测结果最优：VMD-LSTM 方法在k = 4时均方根误差最小，在经度和纬度方向分别为0.039 1 和0.029 3；预测结果与真实结果的相关性最大，相关系数分别为0.881 0 和0.938 5．

基于LSSVM 和LSTM 的方法在经过VMD 处理后，预测结果的均方根误差都明显降低，且相关系数都高于0.800 0．这表明，序列经过VMD 处理后，两种方法都能较为出色地预测深平均流的数值及变化趋势；基于LSSVM 的预测相比基于LSTM 的预测，均方根误差在经度、纬度方向分别降低34%和30%，能得到最优的预测结果．

5 结 论

本文提出了一种利用变分模态分解优化最小二乘支持向量机来预测水下滑翔机深平均流的方法，将分解后的深平均流序列数据分别利用最小二乘支持向量机进行训练，并将各分量的预测结果叠加，得到下一剖面的深平均流预测数据．通过对比其他算法，并经海试试验验证，结果表明：

(1) 基于LSSVM 和LSTM 的方法都能对水下滑翔机的深平均流进行预测，LSSVM 的方法更优；

(2) 将深平均流原始序列数据经VMD 处理后，能明显提升LSSVM 和LSTM 的预测效果，其中VMD-LSSVM 的预测效果优于VMD-LSTM 的预测效果，且在考虑前4 个剖面数据为输入，即k =4 时进行预测的准确性最高；

(3) 将深平均流原始序列数据经过EMD 后，预测结果不稳定，在全序列的预测效果较差．