变分模态分解结合样本熵的变形监测数据降噪
2021-01-07鲁铁定谢建雄
鲁铁定 谢建雄
1 东华理工大学测绘工程学院,南昌市广兰大道418号,330013 2 东华理工大学江西省数字国土重点实验室,南昌市广兰大道418号,330013
变形监测数据包括真实数据和观测噪声,若直接利用原始监测数据进行建模预测难以获得满意结果。在工程应用中一般认为,噪声信号和干扰信号主要分布于高频信号中,而相对平稳的低频信号则被认为是有用的真实信号[1-2]。甘若等[3]运用改进小波阈值函数处理危岩变形沉降数据,能够有效去除噪声,提升信噪比;范千等[4]采用EMD方法降噪处理建筑物形变观测数据,从而获得其形变特征。但小波分析存在小波基选取及确定分解级数等问题,EMD方法存在端点效应与模式混叠等缺点[5]。Wu等[6]通过在原始信号中添加不同的高斯白噪声,提出整体经验模态分解(EEMD)方法,减弱了模式混叠现象的影响,但容易产生较大的重构误差;补充整体经验模态分解(CEEMD)[7]方法尽管提高了完备性和重构精度,但由于集成次数过多导致计算效率低下。
为解决上述问题,Dragomiretskiy等[8]提出一种新型自适应复杂信号分解方法——变分模态分解(VMD)方法,Ram等[9]验证该方法可缓解模态混叠和边界效应,且在鲁棒性、运算效率等方面具有明显优势。同时,根据样本熵(SE)能够反映时间序列复杂程度的特性,本文将其与VMD结合形成一种应用于变形监测数据的新降噪方法,并通过仿真算例和工程实例验证了VMD-SE方法的有效性。
1 算法原理
1.1 VMD算法
不同于EMD方法对信号的剥离,VMD算法是通过设置模态数k、惩罚参数α和上升步长τ等参数将信号分解成k个中心频率为ωk的模态函数uk,其实质为变分问题的构造和求解。VMD算法构造的约束变分问题可表示为:
(1)
式中,f为原始信号,uk为模态函数,ωk为各模态的实际中心频率,e-jωkt为每个解析信号的预估中心频率。
为求解该约束变分模型的最优解,引入拉格朗日乘子λ(t)和二次惩罚因子α,使其转变为无约束变分问题,得到增广拉格朗日表达式为:
L({uk},{ωk},λ)=
(2)
采用交替方向乘子算法,通过迭代更新求得增广拉格朗日表达式的鞍点,即为式(1)最优解。
1.2 样本熵
针对VMD算法不能判定噪声主导的带限固有模态函数(BIMF)的问题,利用样本熵(SE)能够反映信号复杂程度的特性,将其作为判断噪声信号与监测数据有用信号的标准,有效识别形变监测数据有用成分与噪声成分的分界。样本熵的计算过程[10]为:
1)对于长度为N的监测数据信号x(i),按顺序构建m维矢量Xi:
Xi=[x(i)x(i+1)…x(i+m-1)],
i=1,2,…,N-m+1
(3)

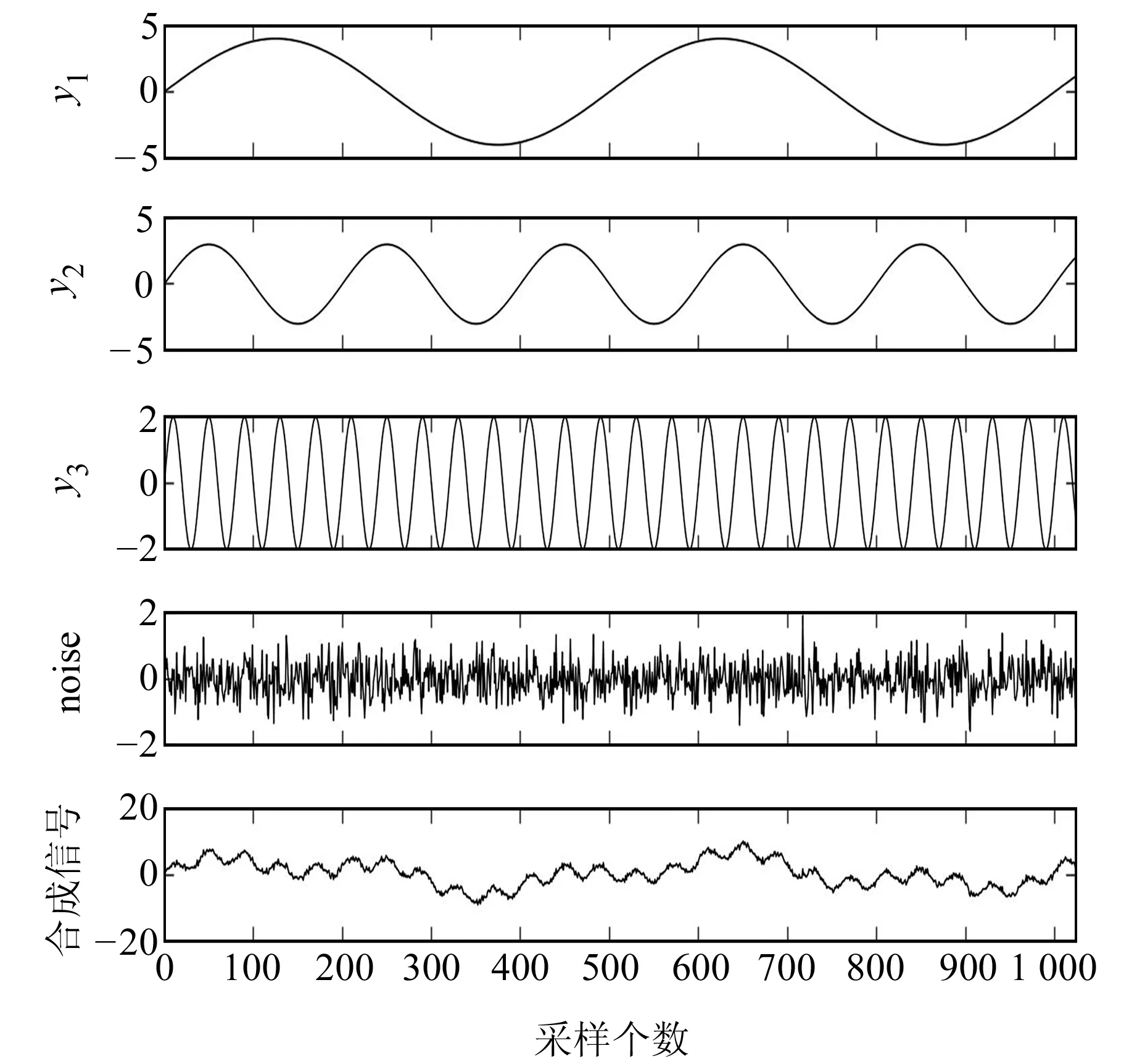
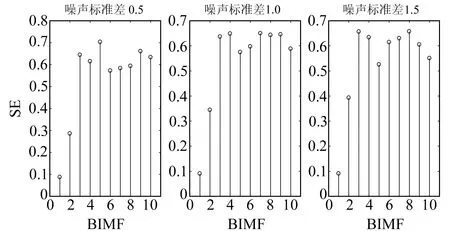
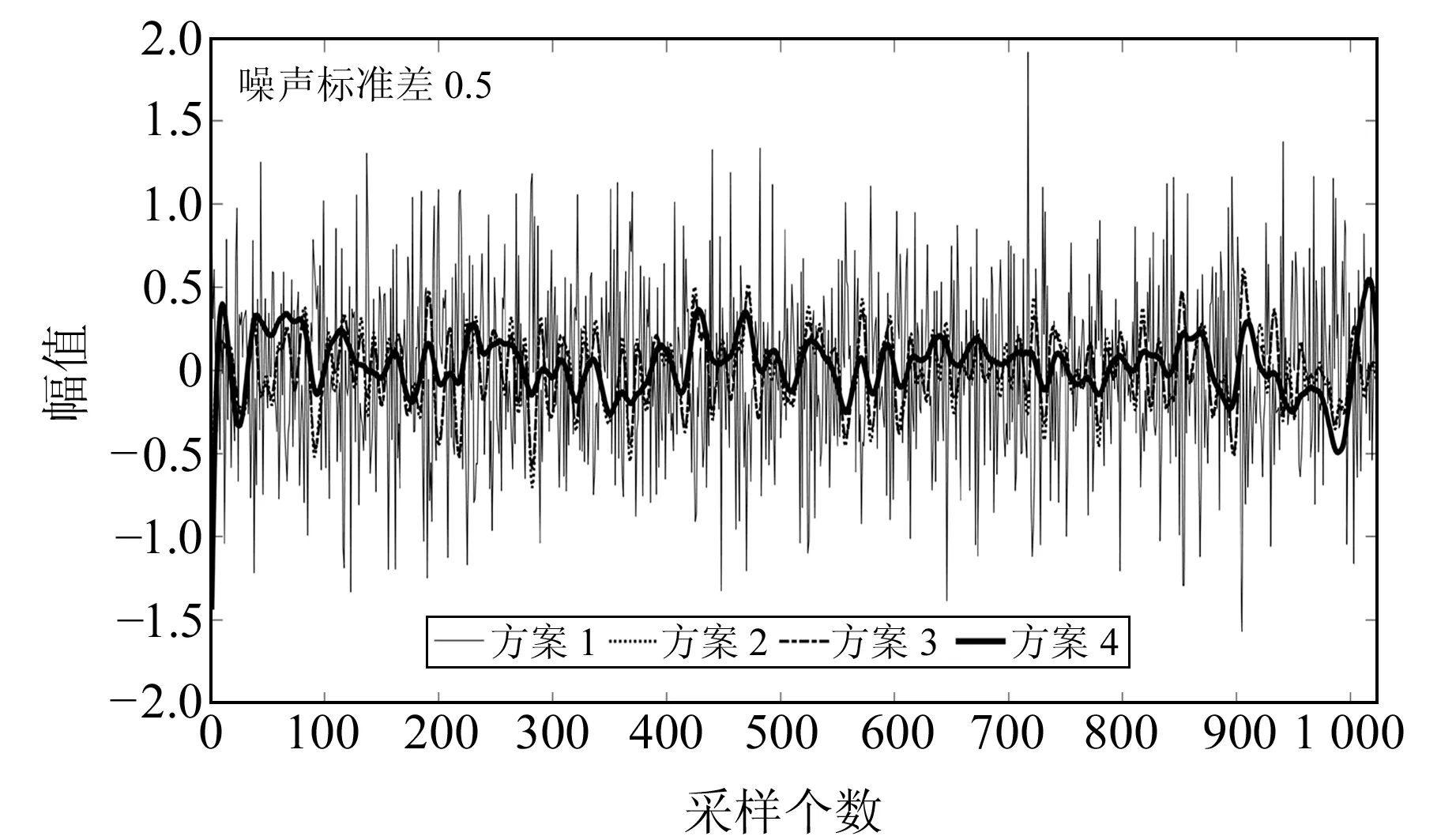
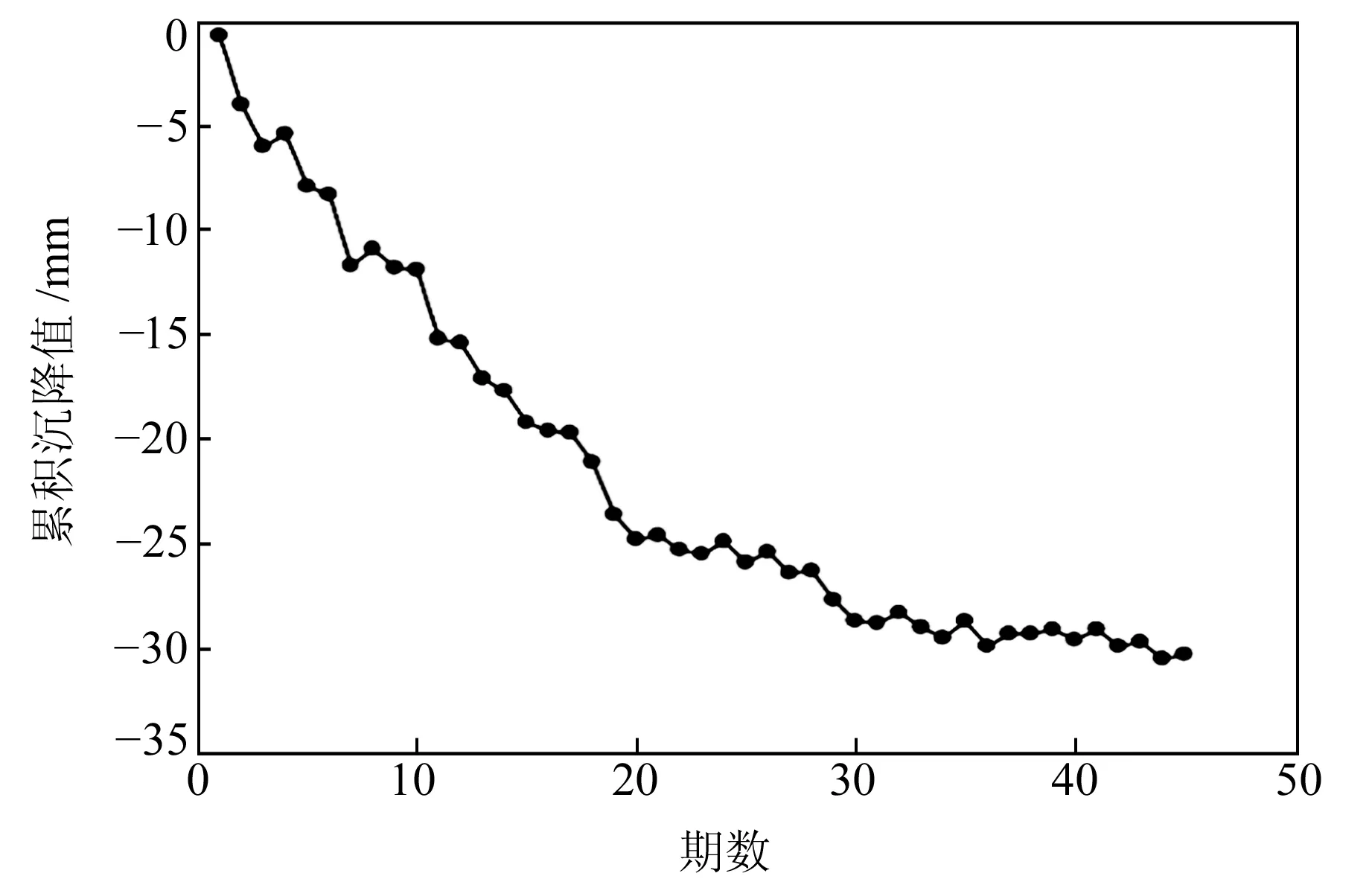
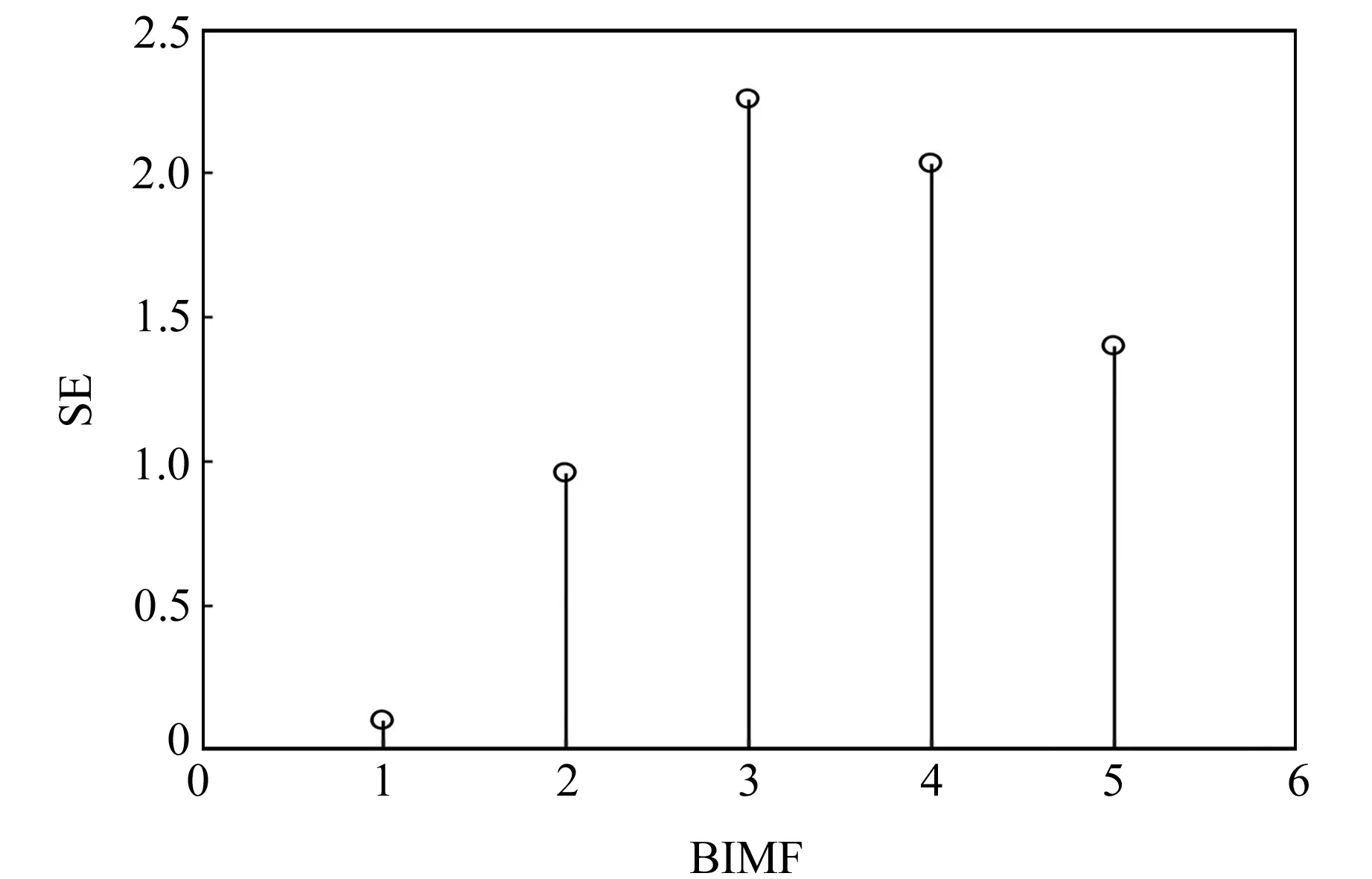
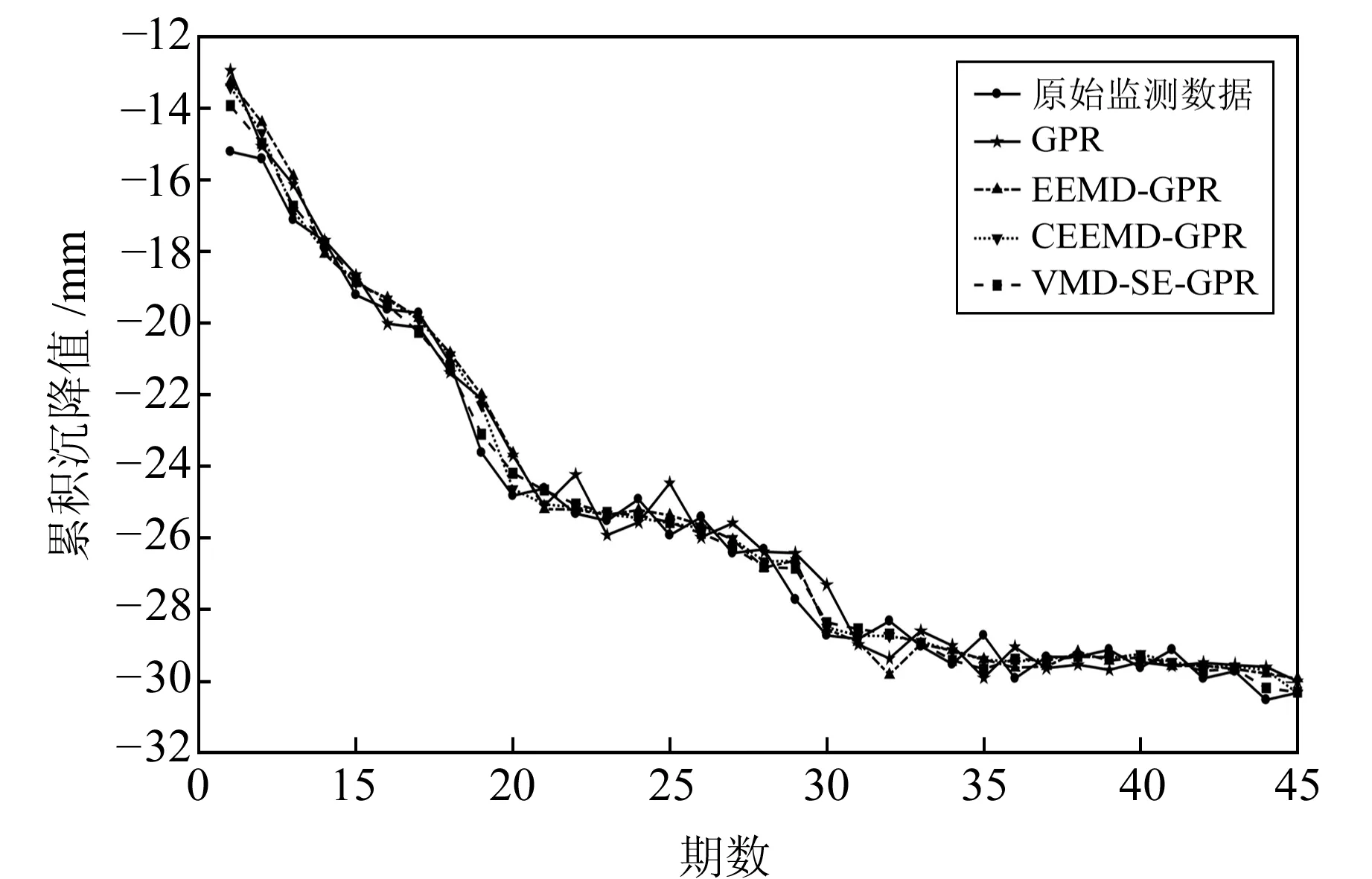
0 (4) (5) (6) 5)更新维数,令m=m+1,并重复上述步骤,即可得到Cm+1(r)。 6)理论上,此时的样本熵为: (7) 当N为有限数时,式(7)可表示为: lnCm(r)-lnCm+1(r) (8) 其中,参数m及r的设定会对样本熵(SE)的值产生较大影响,一般令m=2,r取原始数据标准差(SD)的0.1~0.25倍[11],本文取0.15倍。SE值越大反映信号的随机程度越高,包含的噪声成分越多;相反,SE值越小说明信号的规律性越强,包含的噪声成分越少[12]。 为能较为准确地判断出噪声分量与有用信号分量的界线,阈值的设定尤为重要。文献[12]中将SE阈值设定为0.2,用于区分微地震信号与噪声的分界,取得了不错的效果。但阈值设置得过小易将有效分量误判为噪声分量,导致过度降噪使信号失真;反之,若阈值设置过大也可能对降噪结果产生不利影响。考虑到不同变形体的变形规律差异较大,同时为提高方法的适用性,本文将SE阈值设定为0.5,以尽可能避免有用的非线性变形特征信号被划分为噪声信号而遭滤除。 1)设置VMD算法的相关参数,如模态数k、惩罚因子α及上升步长τ等; 2)原始观测数据经VMD算法分解为k个BIMF,并计算各BIMF的样本熵; 3)将样本熵大于设定阈值的高频BIMF作为随机噪声成分进行滤除; 4)重构剩余的BIMF,获得降噪处理后的观测数据序列。 变形监测信号包含多种噪声,且频率分布范围较广,为保证与实际情况相符,构造复合仿真信号进行模拟实验。仿真信号的采样频率为1 Hz,采样个数为1 024,包括3个周期项和1个趋势项及随机噪声项(图1),其表达式为: 图1 仿真信号Fig.1 Simulation signal Y=4sin(2πt/500)+3sin(2πt/200)+ 2sin(2πt/40)+0.001t+noise (9) 为更好地展现本文方法的降噪效果,分别设置3组标准差噪声水平为0.5、1.0和1.5的高斯白噪声数据,并设置4种实验方案:方案1,未对噪声进行任何处理;方案2,采用EEMD方法降噪;方案3,采用CEEMD方法降噪;方案4,采用本文提出的VMD-SE方法降噪。为对比分析不同算法的处理效果,选用信噪比(SNR)和平滑度(r)[13]指标进行降噪质量评价: (10) (11) 实际变形观测数据中有用成分和噪声的功率均未知,采用信噪比进行降噪质量评价是不合理的,因此引入降噪误差比(dnSNR)[14-15]评价降噪性能,其表达式为: (12) 式中,Ps+n为含噪序列功率,Pg为滤除的噪声功率。 一般认为,SNR越高降噪质量越好,dnSNR及r的值越小降噪效果越显著。EEMD方法及CEEMD方法降噪的关键在于准确识别噪声分量与有效信号分量的分界,本文采用相关系数法[16-17]确定信噪分界。首先计算各阶IMF与原始信号的相关系数,然后寻找相关系数首个极小值出现的第k个IMF,将前k个IMF视为噪声IMF,最后从k+1个IMF开始重构,即可获得降噪后的信号序列。 EEMD方法及CEEMD方法的基本参数设置参考文献[6],VMD算法中模态数k为10(与EEMD模态个数保持一致),惩罚参数α为3 000,上升步长τ为0。图2为加入不同标准差噪声的仿真信号经VMD法分解后各BIMF的样本熵。 图2 不同噪声标准差下各BIMF样本熵Fig.2 Sample entropy of each BIMF with different noise standard deviations 由图2可以看出,在不同噪声水平下,BIMF1和BIMF2的样本熵值均小于0.5,对应为低频有用信号分量;而BIMF3~BIMF10的SE值均大于0.5,对应为高频噪声或虚假模态分量。限于篇幅,本文仅给出噪声标准差为0.5时采用4种方案处理后获得的结果与不含噪声的仿真信号残差,结果见图3。表1统计了不同噪声水平下EEMD、CEEMD及VMD-SE方法的SNR、r及dnSNR值。 图3 4种方案降噪后信号与不含噪声的仿真信号的残差Fig.3 Residuals of the noise-reduced signals and simulated signals without noise of the four schemes 由图3可知,经EEMD与CEEMD降噪处理后的信号与原始参考信号相比存在一定偏差,CEEMD的整体降噪效果略优于EEMD,而采用VMD-SE处理后的信号与原始参考信号的偏差最小。从表1可以看出,在相同噪声水平下,本文方法的SNR值高于EEMD方法和CEEMD方法,平滑度r和dnSNR值也均小于其他两种方法,说明在不同噪声水平下本文提出的新方法的降噪性能具有一定优势。 表1 3种方案降噪评价指标对比Tab.1 Comparison of noise reduction evaluation indexes of the three schemes 某地铁车站基坑由于受到各种不确定因素的影响,如毗邻众多建筑物、场地属于不良地质及施工范围内的城市地下综合管线错综复杂等,施工安全问题非常突出,需随时掌握基坑的动态变化。选取2015-08~2019-04期间沉降监测点M17的45期观测数据进行实验[18],变形曲线见图4。 图4 监测点M17沉降变形曲线Fig.4 Settlement deformation curve of monitoring point M17 由图4可知,该车站基坑沉降实测数据存在较为明显的随机性和不规则性。由于基坑在开挖过程受各种干扰因素的影响,观测数据中包含一定的随机噪声,若直接采用原始观测数据进行建模分析和预测,预测效果往往不佳。这是由于观测噪声会对建模和预测产生较大的干扰,因此需要对原始数据序列进行降噪处理,提高监测数据的质量,进而提高变形预测的精度。 分别采用EEMD、CEEMD及VMD-SE方法对车站基坑沉降序列进行降噪处理,其中EEMD和CEEMD方法的相关参数设置与仿真实验一致。由于车站基坑沉降序列的信噪比较大,EMD法分解后得到的第1阶IMF就包含了绝大部分的噪声,从第2阶IMF开始重构获得降噪后序列[16]。同理,采用EEMD和CEEMD方法进行处理时,也均从第2阶IMF开始重构序列,获取降噪后序列。利用VMD法对观测数据进行分解时,设置模态数k为5(与EEMD分解模态个数保持一致);对于二次惩罚参数α,考虑到基坑序列的噪声水平,同时顾及分解之后序列的保真度[19],经过反复试算,最终确定为0.08,上升步长τ为0。VMD结果见图5,各个BIMF的样本熵见图6。 图5 基坑沉降观测数据VMD结果Fig.5 VMD results of foundation pit settlement observation data 由图5和图6可以看出,VMD方法将基坑沉降时间序列分解成5个由低频至高频的BIMF分量,BIMF1的样本熵值为0.10,其整体趋势与原始监测数据基本保持一致;而BIMF2~BIMF5则表现出较强的随机性,对应的样本熵值均大于0.5,将其作为噪声剔除,以抑制随机噪声对真实数据的干扰。表2为基于不同方法的降噪性能评价指标对比。 图6 各个BIMF的样本熵Fig.6 Sample entropy of each BIMF 表2 降噪性能评价指标Tab.2 Evaluation index of noise reduction performance 由表2可知, VMD-SE降噪方法的平滑度r和dnSNR值均小于另外两种方法,表明新方法的降噪效果最佳。为进一步反映各方法的降噪效果,分别将未经降噪和采用不同方法降噪后获得的前10期沉降观测数据利用高斯过程回归[20](GPR)建立滚动预测模型,以11~45期监测数据作为测试样本数据,用于验证各个预测模型的精度。各方法的预测结果见图7,精度评定见表3。 图7 各方法的预测结果Fig.7 Forecast results of each method 表3 预测精度评定Tab.3 Evaluation of prediction accuracy 由图7可以看出,GPR模型采用未经降噪处理的原始数据进行训练及预测,预测结果的波动性较大;EEMD-GPR和CEEMD-GPR模型去除了一部分观测噪声,预测精度有一定的提高,且CEEMD-GPR模型的预测性能优于EEMD-GPR模型;VMD-SE-GPR模型的预测结果与实测数据最为接近,与表3的统计结果一致,且与文献[18]的WEPM模型相比,预测结果的均方根误差(RMSE)仅为0.44 mm,减小了66.4%。同时与其他方法相比,VMD-SE-GPR模型的预测精度评定指标均为最优,RMSE分别减小了47.6%、38%和18.5%,表明该模型的整体预测精度最高,进一步验证了VMD-SE方法的降噪质量最好,在尽可能保证原始监测数据有用成分的基础上最大限度地滤除了噪声。 本文依据变分模态分解和样本熵各自的优势,提出VMD-SE变形监测数据降噪方法,并通过仿真算例对比分析其信噪比、平滑度、降噪误差比等指标,证实该方法降噪性能优于EEMD方法和CEEMD方法。同时,利用本文方法处理地铁车站基坑变形观测数据,降低了随机噪声信号的干扰影响,有效改善了数据质量,使预测精度得到较大提高,对形变分析具有一定的参考意义。但VMD中分解模态个数k和二次惩罚参数α的预设均会影响最终的分解结果,因此在实际工程应用中如何获取k和α的最佳参数组合,从而得到最优的分解结果,值得进一步深入研究。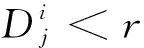
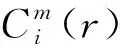
1.3 基于VMD算法的变形监测数据降噪
2 仿真模拟信号分析
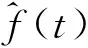

3 实例与分析



4 结 语
