近震波形反演震源机制解方法对比研究
2021-01-07陈俊磊周青云张天继杨黎薇
陈俊磊 周青云 刘 峰 张天继 杨黎薇 赵 昆
1 云南省地震局,昆明市北辰大道148号, 650224 2 中国科学院地质与地球物理研究所岩石圈演化国家重点实验室,北京市北土城西路19号,100029 3 中国科学院大学,北京市玉泉路19号甲,100049
震源机制解现在已成为重要的地震震源参数基础资料产出,针对近震记录发展的波形反演方法主要分为部分特征波形的CAP方法和全波形拟合法,这两类方法均采用网格搜索计算震源机制解,目前已得到广泛应用[1-4]。由于网格搜索方法受台站空间分布、场地效应、地震定位及初始速度模型等因素的影响,反演结果存在非唯一性。采用高频成分能有效提高震源机制解的分辨率,但初始速度模型的不精确使高频成分的拟合变得很困难[5-6]。
利用短周期面波求解近震震源机制解就是一种采用高频信号的拟合方法,该方法在地震足够大、信噪比高且方位角覆盖好时能获得较好的约束[7]。之后发展了将信号截为体波和面波分别进行拟合的CAP方法[1],更加充分地利用了不同震相携带的信息以获取震源机制解,并在该方法基础上引入非双力偶成分分解,即gCAP方法[3]。全波形拟合方法则通过拟合观测波形和由波数积分技术计算的理论地震图来求解震源机制解[8]。不论是部分震相拟合的CAP(或gCAP)方法还是全波形拟合技术,均被证明对速度模型的依赖性较小,但获取的结果存在一定差异[2],两种方法反演得到的倾角和滑动角的误差范围有所不同。为研究两种反演方法的特性及结果存在差异的原因,分别利用两种方法反演鲁甸MS6.5地震的震源机制解,并分析结果的准确性。
1 理论与方法
由震源理论可知,给定地球模型可计算不同震中距和震源深度下的格林函数,而格林函数与震源时间函数卷积并与相应震源机制解线性组合,可得到理论地震图[9]。对于gCAP方法,地震矩张量Dij可分解为各向同性(ISO)、双力偶(DC)和补偿线性矢量偶极(CLVD)等3个分量[3],即
(1)

全波形拟合方法[10]则是在θ、δ、λ空间计算理论地震图,该方法在每次拟合时对理论地震图与接收波形采用相同频率滤波,但不对数据进行截断。通过计算θ、δ、λ参数空间的每组理论地震图并与实测数据拟合得到拟合度,获得的最佳拟合度值对应的震源机制解即为最优解。
2 数据与处理
本文的数据来源于国家测震台网数据备份中心[11],图1为地震震中及台站分布,图中红星即为2014-08-03云南鲁甸MS6.5地震震中,红色倒三角形为gCAP采用的台站,绿色倒三角形为全波形拟合采用的台站,黄色倒三角形为两种方法均采用的台站,两个圆圈分别表示震中距300 km和 500 km。

图1 地震震中及台站分布Fig.1 Distribution of epicenter and stations
gCAP方法采用F-K方法[12]计算格林函数,该方法在Haskell研究[13]的基础上重新定义了传播矩阵,并将静态解与动态解统一到同一公式,提高了计算效率。本文选用震中距300 km范围内的台站数据参与反演,计算前先对数据去仪器响应并旋转到R、T、Z方向,反演时对理论地震图和实测数据使用相同滤波器滤波,Pnl和S波的滤波范围分别为0.05~0.2 Hz和0.02~0.1 Hz,搜索深度步长为1 km,震级步长为0.1,走向、倾角、滑动角的步长均为5°。
全波形拟合方法采用波数积分方法[17]计算格林函数,选用震中距500 km范围内的台站数据进行反演,首先对数据去仪器响应并旋转到R、T、Z方向,再对理论地震图和波形数据采用0.02~0.1 Hz的3 阶Butterworth滤波器同时进行滤波,搜索深度步长为1 km,震级步长为0.1,走向、倾角、滑动角的步长均为5°。
3 结果与分析
图2(a)为本文采用的速度模型[14],图2(b)为gCAP方法反演的波形拟合图。由图可知,Pnl 波被时间窗截断为35 s ,S波被时间窗截断为75 s,波形拟合度较好,数据方位角覆盖良好。震源机制解深度与误差分布(图2(c))显示,最佳拟合矩心深度为3 km,该结果与Xie等[14]采用CAP方法获得的3 km深度的结论一致性较好,与张广伟等[15]采用gCAP方法获得的5 km拟合深度的结论存在一定差异。图3(a)为全波形拟合图,由图可知,受数据信噪比、格林函数计算精度、速度模型准确度等的影响,部分台站数据会不可避免地出现拟合度较差的情况,将其剔除以获得较好的拟合结果。由全波形反演的不同深度震源机制解误差分布图(图3(b))可知,最佳拟合质心深度为10 km。综上所述,不同研究人员利用近震资料拟合的矩心深度存在差异,表明近震资料对矩心深度的约束不足,还需进一步采用深度震相等其他参数加以约束。

图2 鲁甸MS6.5地震震源机制解Fig.2 Focal mechanism solution of Ludian MS6.5 earthquake

图3 鲁甸MS6.5地震全波形拟合图Fig.3 Full waveform fitting map of Ludian MS6.5 earthquake
表1为不同研究机构或研究人员及本文计算的鲁甸地震震源机制解,其中美国地质调查局(USGS)和美国哥伦比亚大学全球矩心矩张量解中心(Global CMT,前哈佛大学矩心矩张量中心)分别采用远震体波和面波测定地震的震源机制解,两组解基本一致。根据余震精定位[16]表明,鲁甸地震的发震构造为N-NW(155°)和E-NE(265°)向两条断裂;根据野外地质和地表破裂考察[17]判定,发震断层应为近EW向的包谷垴-小河断裂,为左旋走滑型地震,该断层的走向与表1中节面Ⅱ的走向比较吻合。由表1可知,近震方法反演的鲁甸地震震源机制解(节面Ⅱ)走向为73~77°,有很好的一致性;本文采用gCAP和全波形两种方法获得的走向分别为256°和254°,与其他结果较为一致。对于倾角而言,除文献[14]和文献[18]外,其余结果均大于70°,而本文得出的滑动角在扣除走向方向效应(即旋转180°)后,与其他结果基本一致,表现为近走滑。
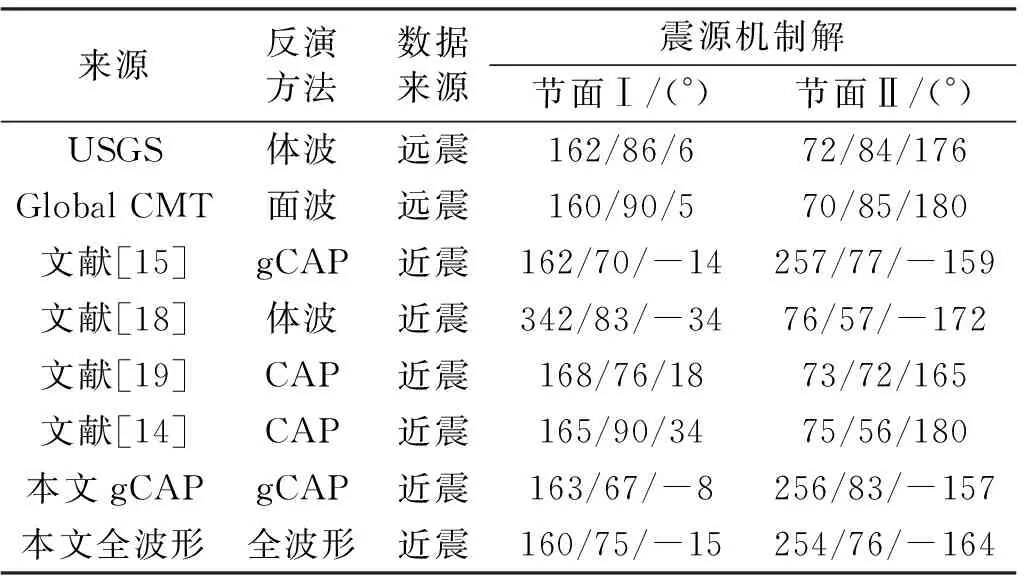
表1 不同研究人员发布的鲁甸地震主震震源机制解Tab.1 The focal mechanisms from different research groups
4 结 语
通过分析可以得到以下结论:1)本文采用gCAP和全波形两种反演方法计算鲁甸MS6.5地震的震源机制解,获得了较为一致的结果;2)gCAP方法采用震中距300 km范围内方位角覆盖良好的台站数据,能得出较为稳定的结果;3)在运用全波形反演方法时,需扩大台站选取范围,并增加台站数量,以提高数据的拟合程度,增加结果的稳定性;4)近震资料对矩心深度的约束不足,需进一步采用深度震相等其他参数加以约束。
