估计卫星频间偏差的GLONASS伪距定位改进模型及其验证
2021-01-07陈俊平
刘 姣 陈俊平 王 彬
1 中国科学院上海天文台,上海市南丹路80号,200030 2 中国科学院大学,北京市玉泉路19号甲,100049
由不同类型测距码产生的两类信号之间的时延差异称为差分码偏差(differential code bias, DCB)。对于采用码分多址(code division multiple access, CDMA)技术的GNSS系统(GPS、BDS、Galileo、QZSS等)而言,由于卫星频率相同,在建立电离层延迟模型的过程中,可同步分离硬件延迟差异与电离层延迟,从而获得卫星端与接收机端硬件延迟差异之和[1-2]。而GLONASS系统采用频分多址(frequency division multiple access, FDMA)方式传输信号,其频率在卫星间存在差异,因此其硬件延迟中包含与频率相关的IFB[3-4]。由于该偏差不能作为公共误差被接收机钟差吸收,从而会对GLONASS系统建立电离层延迟模型造成影响。研究表明[5-6],GLONASS频间码偏差可高达数米,将严重影响定位精度。国内外学者[6-12]基于精密星历和钟差产品对接收机端频间码偏差进行了大量研究,本文针对GLONASS广播星历中群延迟TGD(timing group delay)参数的缺失问题,基于伪距残差分析研究GLONASS系统卫星端和接收机端频间码偏差的特性,建立广播星历的频间偏差和伪距定位改进模型,并对改进的定位模型进行动态定位验证。
1 GLONASS广播星历精度分析
广播星历中轨道和钟差的精度会影响其导航定位的性能。以欧洲定轨中心(CODE)的精密星历和钟差为基准,计算广播星历和精密星历的差异,并对GLONASS的广播星历精度进行分析。对比两类参数时需考虑以下因素:
1)时间基准差异:GLONASST与UTC保持一致,与GPST之间存在跳秒差异,在比较时需进行时间系统基准差异修正;
2)相对论改正:GLONASS广播星历钟差中包含钟差相对论改正,在与精密钟差比较时需扣除钟差相对论改正;
3)钟差基准差异:选取当前历元所有健康卫星广播星历与精密星历钟差差异的中位数,扣除卫星钟差基准的差异;
4)卫星天线相位中心改正:精密星历的参考点为卫星质量中心,广播星历的参考点为天线相位中心,广播星历与精密星历的PCO值差异为钟差差异,其中广播星历的PCO值使用文献[13]中给出的值,精密星历的PCO值根据igs14_1930.atx确定。
在以上改正的基础上,以CODE精密产品为基准,计算GLONASS各卫星的空间信号精度。空间信号精度SISURE为卫星轨道误差与钟差误差的综合,其计算公式为[7]:
(1)
(2)
式中,投影系数α、β分别取值0.98、1/45,N、T、R为卫星轨道坐标系中法向、切向和径向误差,clk为钟差误差,SISURE_orb为轨道空间信号精度。
采用2018-01-01~01-07的数据进行分析,表1(单位m)为所有卫星轨道误差、钟差误差以及空间信号精度误差的分析结果。从表1可以看出:1)轨道误差中切向和法向的离散度较大,径向的精度最高;2)轨道误差中包含的周期项与卫星运行周期强相关;3)GLONASS卫星钟差误差存在不同程度的系统误差,处在同一频点的两颗卫星的钟差误差可能相差很大,如R09和R13卫星的钟差误差相差约5 m;4)空间信号精度误差的主导因素为钟差误差,而相同频率卫星存在明显的系统差异。

表1 GLONASS广播星历误差和空间信号精度统计Tab.1 Statistics of GLONASS broadcast ephemeris errors and SISUREs
上述分析表明,GLONASS广播星历中钟差误差为最大的误差来源,并且不同卫星的钟差误差存在显著的系统性差异。造成差异的原因一方面为广播星历中卫星钟差的预报误差,另一方面为广播星历中未提供卫星端的通道延迟(包含卫星间频率不同造成的频间偏差)。
2 GLONASS广播星历频间偏差模型
基于广播星历,传统伪距定位数学模型可表示为:
(3)
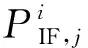
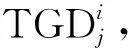
(4)
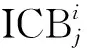
(5)
2.1 精密星历伪距定位残差分析
基于精密星历和钟差产品,无电离层组合伪距定位方程可表示为:
(6)
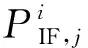


(7)


表2 测站接收机及天线配置情况Tab.2 Conditions of station receivers and antennas
以AREG和RDSD站为例分析卫星R01、R02、R03的伪距残差时间序列(图1)。由图可见,各颗卫星的伪距残差具有非零均值特性,两个测站R01、R02、R03的伪距残差均值分别为-0.20 m、-1.1 m、1.6 m和-0.75 m、-0.61 m、1.68 m。

图1 基于精密星历的伪距残差时间序列Fig.1 Pseudorange residuals time series based on GLONASS precise ephemeris
图2为4个测站伪距残差均值与频率号的对应关系,表3为各颗卫星的频率。由图可见,各颗卫星的伪距残差均值与对应的频率号存在极强的线性关系。由于精密卫星钟差已包含卫星端的频间偏差,而接收机端的公共硬件延迟会被接收机钟差吸收,因此伪距残差中与频率号线性相关的部分为接收机端频间码偏差。通过线性拟合可以发现:1)频率号为0时,拟合直线上所对应的伪距残差值接近于0;2)各测站的斜率与接收机和天线类型有关。若接收机、天线类型完全相同,则斜率一致;若两者中有一个不同,则斜率存在差异甚至反向(KOKV和WIND测站)。对全球其他TRIMBLE NETR9、JAVAD TRE_G3TH DELTA接收机的数据进行相同的分析,均可得出类似结论。

表3 卫星PRN编号与频率号对应关系Tab.3 Correspondence between satellite PRN number and frequency number

图2 基于精密星历的伪距残差均值与频率号的对应关系Fig.2 Correspondence between means of pseudorange residuals and frequency numbers based on GLONASS precise ephemeris
根据上述分析可知,接收机端频间码偏差与卫星频率号的函数关系为:
(8)
式中,k为卫星频率号;Δb为邻频频间码偏差,即GLONASS卫星频率编号相差为1时频间码偏差值。

(9)
基于式(9)并采用与前文一致的处理策略重新进行伪距定位数据处理,获得AREG、RDSD测站R01、R02、R03卫星的伪距残差时间序列(图3)。由图可见,3颗卫星的伪距残差非零均值特性得到大幅消除,R02、R03卫星表现尤为明显;AREG测站伪距残差均值由-1.1 m、1.6 m减小到0.1 m、0.6 m,RDSD测站伪距残差均值由-0.6 m、1.7 m减小到0.2 m、0.8 m。测站AREG、RDSD、KOKV和WIND的邻频频间码偏差Δb的标准差分别为1.8 cm、1.1 cm、1.2 cm、1.2 cm,各天的Δb值相近,表明接收机端的频间偏差具有长期稳定性。图4为该时间段伪距残差均值与频率号的对应关系,由图可见,引入接收机端频间码偏差函数模型后,伪距定位残差与频率号之间的线性相关特性得到消除,且各卫星的伪距残差均值范围由±1.5 m下降为±1 m。

图3 基于接收机频间偏差模型的伪距残差时间序列Fig.3 Pseudorange residual time series based on receiver dependent inter frequency bias model
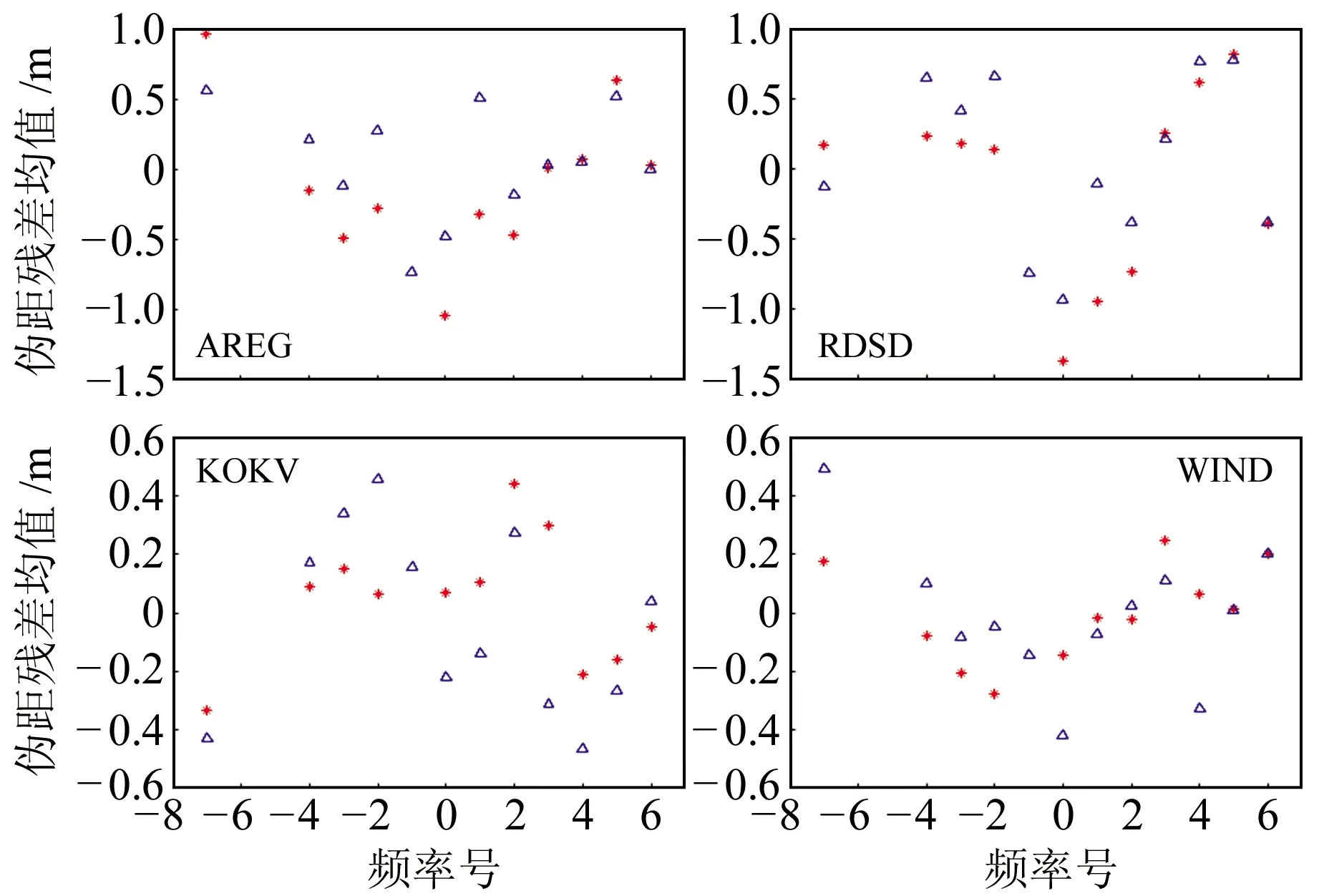
图4 基于接收机频间偏差模型的伪距残差均值与频率号的对应关系Fig.4 Correspondence between means of pseudorange residuals and frequency numbers based on receiver dependent inter frequency bias model
采用CNMC方法能够降低伪距观测值的噪声,但对伪距进行平滑前后计算所得到的邻频频间码偏差Δb值相差很小,因此本文不再赘述。
2.2 改进的GLONASS广播星历伪距定位模型
§2.1分析表明,接收机端频间偏差可通过线性模型进行改正。在此基础上,将§2.1中接收机端频间码偏差线性模型引入GLONASS广播星历定位模型,则式(5)可写为:
(10)
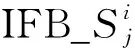
式(10)即为GLONASS广播星历改进定位模型。基于同样的观测数据,采用GLONASS广播星历,利用改进的定位模型对数据进行处理。模型中接收机和卫星端频间码偏差可利用历史观测数据预报获取,也可采用模型进行直接估计,本文将接收机端频间偏差和卫星端频间偏差这两个参数作为待估参数进行处理。图5为AREG、RDSD测站伪距定位的残差时间序列,由图可见,伪距残差近似符合零均值条件,AREG、RDSD测站R01、R02、R03卫星的伪距残差均值分别为0.03 m、0.07 m、-0.05 m和0.19 m、0.09 m、-0.07 m。

图5 GLONASS广播星历改进定位模型的伪距残差时间序列Fig.5 Pseudorange residual time series of the modified positioning model based on GLONASS broadcast ephemeris
图6为基于改进的定位模型而确定的各测站卫星伪距残差均值与频率号的对应关系,由图可见,多数卫星的伪距残差均值在±0.4 m以内。相比于图4,由于残余误差被卫星端频间码偏差所吸收,图6中各卫星的伪距残差均值都得到进一步改善。
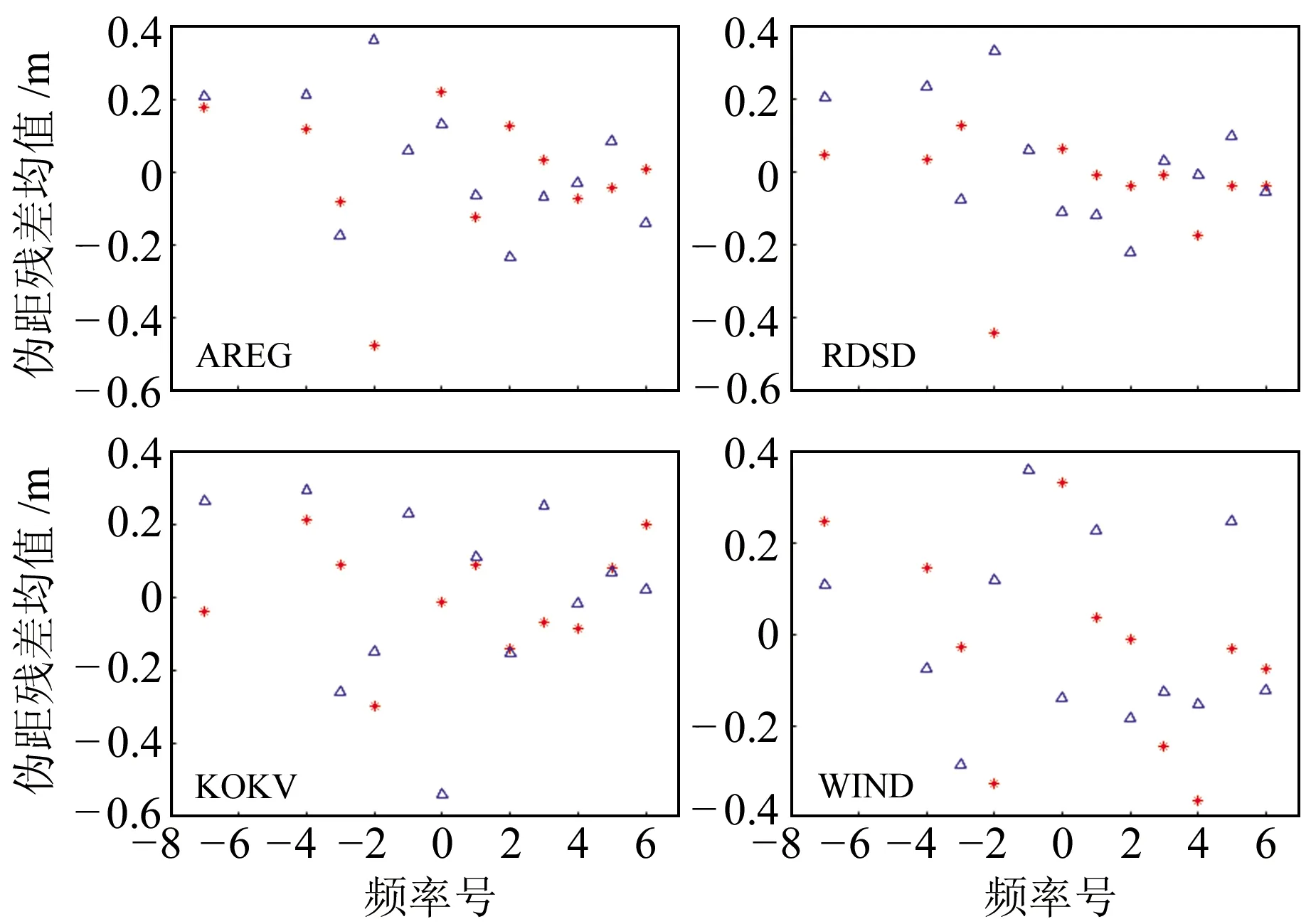
图6 GLONASS广播星历改进定位模型伪距残差均值与频率号的对应关系Fig.6 Correspondence between frequency numbers and means of pseudorange residuals of the modified positioning model based on GLONASS broadcast ephemeris
3 GLONASS广播星历改进定位模型验证
为验证GLONASS广播星历改进定位模型的可靠性,选取分布于全球的25个测站进行定位验证,涉及的接收机主要为TRIMBLE NETR9和JAVAD TRE_G3TH DELTA两种类型,采用动态定位模式进行伪距定位处理。测站分布如图7所示。

图7 定位模型验证所选测站分布Fig.7 Distribution of the selected stations for the positioning model verification
分别采用传统模型以及改进模型对数据进行分析。改进模型在传统模型的基础上已修正测站的频间偏差,并估计每颗卫星的频间差。图8为4个测站2018-01-01两种广播星历伪距定位模型的动态定位时间序列,可以看出,改进模型获得的定位精度明显优于传统模型,动态定位误差相对集中,且偏离值较小。另外,图中定位结果的不连续是由于所选取的4个测站均处于低纬度地区,同时受限于卫星高度角,使得部分时段卫星数目少于定位需求的卫星数。
图9为25个测站2018-01-01~01-07连续7 d在N、E、U三个方向上动态定位结果的RMS值,可以看出,N、E、U三个方向的平均定位精度由3.89 m、3.87 m、11.02 m提高至1.89 m、2.23 m、5.77 m,平均精度分别提高51.1%、41.7%、48.3%。

图9 基于GLONASS广播星历不同定位模型的RMS值Fig.9 RMS of the traditional and modified positioning models based on GLONASS broadcast ephemeris
4 结 语
利用GLONASS广播星历进行伪距定位的主要误差源包括广播星历轨道误差和钟差预报误差、接收机端频间偏差以及卫星端频间偏差。通过分析GLONASS广播星历空间信号精度发现,GLONASS各卫星广播星历钟差误差存在显著的系统性差异,其来源一方面为卫星钟差的预报误差,另一方面为广播星历中未标定的卫星群延迟。
基于GLONASS精密星历和钟差定位的伪距残差呈现出系统偏差,最大值可达2 m,该系统偏差主要为接收机端的频间偏差,且与卫星频率号具有线性相关性。将此频间偏差模型引入传统的GLONASS伪距定位模型,并考虑卫星端的频间偏差参数,建立基于广播星历的伪距定位改进模型,同时对改进模型进行动态定位验证。结果表明,伪距定位改进模型相对原有模型在N、E、U三个方向的精度分别提高51.1%、41.7%、48.3%。