长三角地区GNSS大气水汽转换系数模型精化研究
2021-01-07侯晓玲张雯雯周嘉陵管仲培
侯晓玲 张雯雯 李 黎,2 周嘉陵 刘 宇 高 颖 管仲培
1 苏州科技大学环境科学与工程学院,苏州市学府路99号,215009 2 苏州科技大学北斗导航与环境感知研究中心,苏州市学府路99号,215009 3 江苏省气象科学研究所,南京市昆仑路16号,210009
水汽主要分布在对流层底部,是大气变化监测中极为重要的气象参数之一,因此获取高时空分辨率的水汽资料对气象预报和气候监测具有重要意义[1]。获取水汽资料的传统手段主要包括探空气球、微波辐射计和红外遥感等,这些观测方法存在时空分辨率低、成本较高或工作量大等问题。随着GNSS技术的发展,利用地基GNSS站能反演得到高时空分辨率的大气可降水量(precipitable water vapour, PWV)[2]。由GNSS得到的天顶总延迟(zenith total delay, ZTD)减去天顶干延迟(zenith hydrostatic delay, ZHD)得到天顶湿延迟(zenith wet delay, ZWD),ZWD,乘以水汽转换系数(K值)就可以获得GNSS-PWV,可见K值是地基GNSS-PWV反演中的一个关键参数。
文献[2]首次利用探空资料建立加权平均温度(Tm)与地表温度(Ts)的关系模型,再通过将Tm值转换为K值来实现任意位置的K值计算;文献[3-4]利用探空资料建立了几种全球非气象参数Tm模型,但是这些模型在局部地区的适用性有待进一步验证。目前能够利用积分法精确获得K值[5],但因计算较复杂,已经不能满足实时发展的要求。文献[6]利用中国地区84个探空站2010~2015年的探空数据计算K值,分析其时空变化特征,得出一种仅与地理位置信息和年积日有关的改进的K值模型,发现K值随纬度和高程的增大而明显减小;文献[7-8]在中国低纬度地区和新疆地区建立精化Emardson模型,并取得较好的精度;文献[9]利用不同的K值模型反演拉萨站的GNSS-PWV,其结果与探空PWV具有较好的一致性,表明顾及高程的Emardson-H模型适用于缺乏气象参数的高海拔地区。
从以上分析可知,Emardson模型具有地方性差异,因而要获得较高的应用精度需要基于当地的探空资料建立本地的精化模型。本文利用长三角地区 7 个探空站(上海、南京、射阳、阜阳、安庆、杭州和衢州)数据通过数值积分法计算的K值,分别建立2016年的两个Emardson精化模型,并利用2017年的K值验证两个模型的预报精度。
1 数据处理方法
1.1 积分法求K值
精确的K值可通过积分法计算探空数据得到:
(1)

(2)
式中,Pvi、Ti、Δhi为第i层大气的平均水气压、平均温度和大气厚度。
1.2 Emardson建模方法
Emardson等[10]利用欧洲数10个探空站数据,基于K值时空变化特性,建立了一种顾及纬度和年积日的K值模型(简称Emardson模型)。由于Emardson模型与气象参数无关,且精度较好,因此在实时GNSS水汽反演中有很好的应用潜力。
不顾及高程的Emardson-I模型为:
(3)
文献[7-8]表明,K值与高程有一定的相关性。因此,在式(3)的基础上建立顾及高程的Emardson-H模型:
(4)
式中,φ为大地纬度,doy为年积日,H为海拔,α0、α1、α2、α3、α4为模型系数。
1.3 精度评估方法
本文采用平均绝对偏差(MAE)和均方根误差(RMS)来评价模型的精度:
(5)
(6)
2 Emardson建模及其精度分析
2.1 数据来源及建模
探空数据来自美国怀俄明大学大气数据网(http: //weather.uwyo.edu/upperair/sounding.html),该机构以世界气象组织制定的规则为依据,已对其发布的探空数据进行质量检查,包括重复值检查、垂直一致性检查、极端观测值检查、气候界限值检查和流体静力学一致性检查[11]。选用2016~2017年长三角地区7个探空站(安庆、阜阳、杭州、衢州、上海、射阳和南京)每天两次采集的探空数据(上海和南京的垂直分辨率为500 m,其他5个站为1 000 m),主要包括气压、高度、温度、露点和相对温度等气象参数。图1是长三角地区7个探空站和2个GNSS站的分布图,表1是7个探空站的位置信息。

图1 长三角地区7个探空站和2个GNSS基准站的地理分布Fig.1 Geographical distribution of 7 radiosonde and 2 GNSS stations in the Yangtze river delta

表1 长三角地区探空站位置信息Tab.1 Location information of sounding radiosonde in the Yangtze river delta
采用2016年7个探空站计算的K值,分别建立Emardson-I模型和Emardson-H模型,利用最小二乘法进行多元线性拟合求出模型系数(表2),分析Emardson-I和Emardson-H模型2017年的K值预报精度。

表2 Emardson-I和Emardson-H模型系数Tab.2 Model coefficient of Emardson-I and Emardson-H
2.2 K值精度分析
以积分法计算的K值作为真值,分别与2017年Emardson-I和Emardson-H模型预报的K值作对比得到差值散点图(图2)。由图可知,Emardson-I和Emardson-H模型预报的K值与积分法计算的K值差别很小。由表3可得, Emardson-I模型的平均绝对偏差均值为0.001 303、均方根误差均值为0.001 620,Emardson-H模型的平均绝对偏差均值为0.001 297、均方根误差均值为0.001616,Emardson-H模型的MAE和RMS分别降低1.5%和1.2%。由此看出, Emardson-H模型略优于Emardson-I模型,但提高有限。

图2 安庆站和射阳站的偏差分布Fig.2 Deviation distribution of Anqing station and Sheyang station

表3 Emardson-I与Emardson-H的K值精度统计Tab.3 Accuracy statistics of K-value for Emardson-I and Emardson-H
2.3 GNSS-PWV精度
首先用精密单点定位(PPP)技术解算得到高精度的GNSS-ZTD(小于6 mm),ZTD的时间分辨率为5 min[12],再根据Saastamoinen模型计算ZHD,ZTD减去ZHD可得到ZWD,而ZWD乘以K值即可得GNSS-PWV。以2017年安庆和射阳的探空PWV作为参考值,使用其并址GNSS数据,来检验Emardson模型的GNSS-PWV反演精度。
由图3可知,Emardson-I模型和Emardson-H模型之间差别很小,其GNSS-PWV反演结果与探空PWV有较好的一致性。

图3 安庆站和射阳站的GNSS-PWV偏差Fig.3 GNSS-PWV deviations at Anqing and Sheyang stations
由表4可知,Emardson-I模型的MAE和RMS分别为0.368和0.548,Emardson-H模型的MAE和RMS分别为0.370和0.552,两种模型精度相差不大,原因是安庆站与射阳站均位于低海拔地区,顾及高程的作用几乎可以忽略不计。
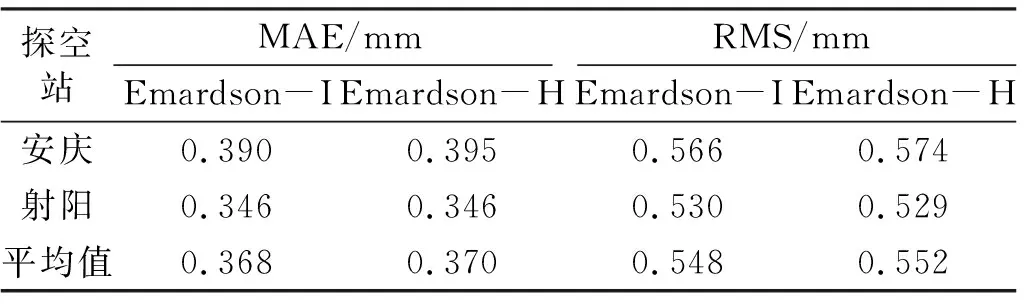
表4 基于Emardson-I和Emardson-H的GNSS-PWV精度统计Tab.4 Accuracy statistics of GNSS-PWV from Emardson-I and Emardson-H
3 结 语
1)Emardson-I模型的MAE和RMS分别为0.001 303和0.001 620,Emardson-H模型的MAE和RMS分别为0.001 297和0.001 616,后者的K值预报精度略有提高。
2)就GNSS-PWV而言,Emardson-I模型的MAE和RMS分别为0.368 mm和0.548 mm,Emardson-H模型的MAE和RMS分别为0.370 mm和0.552 mm,二者均优于0.6mm。
3)由于Emardson-I和Emardson-H的K值预报精度和GNSS-PWV反演精度相当,Emardson-I模型以其无需实测气象参数和不顾及高程的效率优势,在缺乏地面气象资料的低海拔地区具有更好的适用性。
