Almost Sure Exponential Stabilization of Hybrid Stochastic Differential Equations with Variable Delays

LI Guangjie(李光洁)

( School of Mathematics and Statistics，Guangdong University of Foreign Studies，Guangzhou 510006，China)

Abstract: This paper deals with the almost sure exponential stability of the multidimensional hybrid stochastic differential equation (SDE) with variable delays dy(t)=f(y(t-δ1(t))，r(t)，t)dt+g(y(t-δ2(t))，r(t)，t)dω(t)，where δ1(·)，δ2(·):R+ →[0，τ]represent the variables delays and r(t) is a Markov chain.By applying the Lyapunov technique，the stochastic analysis and the Borel-Cantelli lemma，it is shown that under given conditions there exists a positive constant such that the hybrid SDE with variable delays is almost surely exponentially stable as long as τ ＜ if the corresponding hybrid SDE dx(t) = f(x(t)，r(t)，t)dt + g(x(t)，r(t)，t)dω(t) is almost surely exponentially stable.This generalizes and improves some results obtained in the existing literature.

Key words: Almost sure exponential stability; Hybrid stochastic differential equation;Stochastic stabilization; Delay feedback control

1.Introduction

Stochastic hybrid systems combine a part of the state that takes continuous values and another part of the state that takes discrete values.As we know，such systems have been widely used in many branches of science and industry to model systems where they may experience abrupt changes in their structure and parameters[1].One of the important classes of the stochastic hybrid systems is the SDEs with Markovian switching (SDEwMSs).In the study of the SDEwMSs，automatic control with the emphasis being on stability analysis is always one of the most important issues.[2]

It is well known that there are many results on the stochastic stabilization of SDEwMSs.On the one hand，in the case of the continuous-time feedback control，MAO et al.[3]designed a delay feedback control in the drift part.Based on such a feedback control，that paper concerned with the exponential mean-square stabilisation of SDEwMSs.FEI et al.[4]investigated the stabilization for a class of Markovian jump linear systems with time delay and the authors in the paper also designed the delay feedback control in the drift term.Other results contributed to the stabilization by the continuous-time feedback control for such equations have been discussed in [5-6] and the references therein.On the other hand，in the case of the discrete time state observations，MAO[7]is the first paper that proposed a new feedback controller based on discrete-time state observations and concerned with the mean-square exponential stabilization of continuous-time SDEwMSs.Since then，part of results have been obtained on the stabilization by the discrete-time feedback control for SDEwMSs.[8-11]But it should be pointed out that the results mentioned above either the feedback control is only designed in the drift term or the delay feedback control is designed based on discrete time state.

Motivated by [12]，this paper is considered with the almost sure exponential stability of the multidimensional SDDEwMS with variables delay of the form

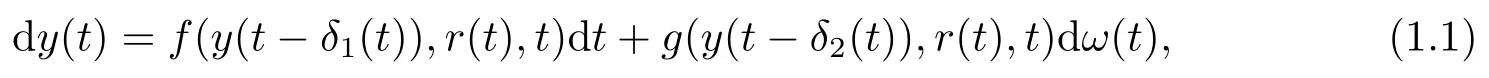
where δ1(·)，δ2(·):R+→[0，τ] are the variable delays and r(t) is a Markov chain.It is shown that if the corresponding hybrid SDE ((1.1) without variable delays)

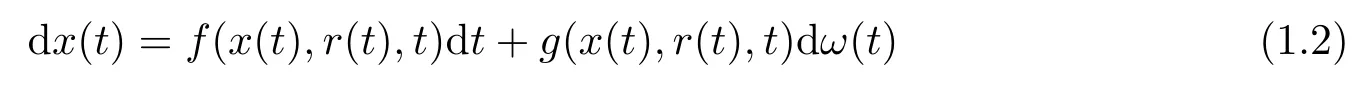
is almost surely exponentially stable，then there exists a positive constantsuch that the SDDE (1.1) is also almost surely exponentially stable with τ ＜.Moreover，the implicit lower bound for τ can be computed numerically.The theory in this paper can be used in the area of stochastic stabilization and one can design delay feedback controls in both the drift coefficient and diffusion coefficient to stabilize the given hybrid SDEs.

The rest of this paper is organized as follows.In Section 2，some preliminaries and problems are given.In Section 3，main results are established.

2.Preliminaries and Problem Statement

Throughout this paper，let |x| =be the Euclidean vector norm of vector x ∈Rnand R+= [0，+∞).For a，b ∈R，we use a ∨b and a ∧b for max{a，b} and min{a，b}，respectively.Let (Ω，F，{Ft}t≥0，P) be a complete probability space with a filtration {Ft}t≥0satisfying the usual conditions.Let ω(t)=(ω1(t)，··· ，ωm(t))Tbe an m-dimensional Brownian motion defined on the probability space.For some τ ＞0，let C = C([-τ，0];Rn) be the family of all continuous Rn-valued functions ξ with the normFor t ≥0，definethe family of all Ft-measurable Rn-valued random variables η with E|η|2＜∞，and(Ω;C([-τ，0]);Rn)the family of Ft-measurable C-valued random variables ξ satisfying E‖ξ‖2＜∞.Let {r(t)}t≥0be a right-continuous time-homogeneous Markov chain (independent of ω(·)) on the probability space taking values in a finite state space S ={1，2，··· ，N} with the generator Γ =(γij)N×Ngiven by

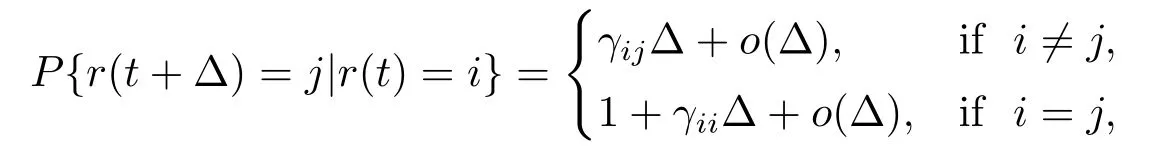
where Δ ＞0.Here γij≥0 is the transition rate from i to j，if ij，whileMoreover，as a standing hypothesis we assume that the markov chain r(t) is irreducible，namely，the Markov chain has a unique stationary(probability)distribution π =(π1，...，πN)∈R1×Nwhich can be determined by solving πΓ =0 subject to ∑=1 and πj＞0 for j ∈S.[2]It is well known that almost every sample path of the Markov chain r(·) is a right-continuous step function with finite number of simple jumps in any finite subinterval of R+.[13]

Consider an n-dimensional hybrid SDDE of the form

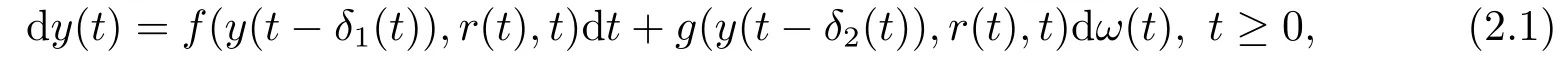
with initial data y(u)=ξ(u)∈Ω;C([-τ，0]，Rn)for u ∈[-τ，0]and r(0)=r0∈S，where δ1，δ2:R+→[0，τ]are Borel measurable.The drift and diffusion coefficients f :Rn×S×R+→Rnand g :Rn×S×R+→Rn×m.

As a standing hypothesis，we impose the global Lipschitz condition holds as follows.

Assumption 2.1Assume that both f，g satisfy the global Lipschitz condition，that is，there exists a positive constant L such that for any x，y ∈Rn，t ≥0 and i ∈S

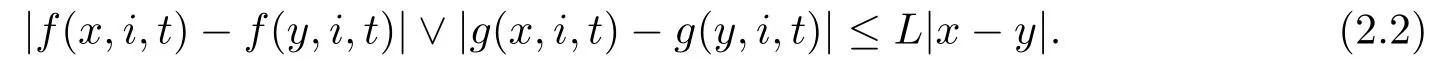
Moreover，in order to study the stability of Eq.(2.1)，we assume that f(0，i，t)=g(0，i，t)=0 for all (i，t) ∈S×R+，then Eq.(2.1) admits a trivial solution y(t;0) ≡0.It is easy to see that Assumption 2.1 implies the linear growth condition

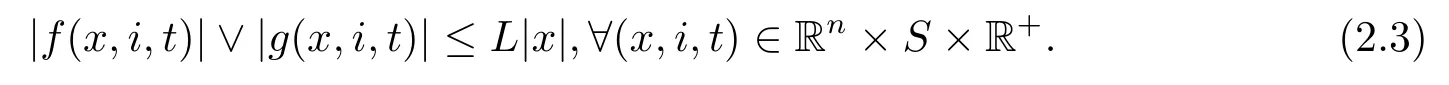
Under Assumption 2.1 (this assumption also implies f，g satisfy the local Lipschitz condition)，Eq.(2.1) has a unique solution on t ≥-τ and the second moment of the solution is finite (see [2]，Theorem 7.10).Denote by y(t;ξ，r0)=y(t) with initial value (ξ，r0)∈Rn×S.Moreover，define yt={y(t+u):u ∈[-τ，0]}on t ≥0，therefore ytis an Ft-adapted C-valued stochastic process and yt∈(Ω;C([-τ，0]，Rn)).Furthermore，for any 0 ≤s ≤t ＜∞，we denote by yt= y(t;s，ys，r(s)) with initial data ys，r(s) at t = s.For Eq.(2.1)，given ysat time s，we can determine x(t) for all t ≥s，but how the solution reaches ysis of no use.

The corresponding hybrid SDE for Eq.(2.1) is as follows:

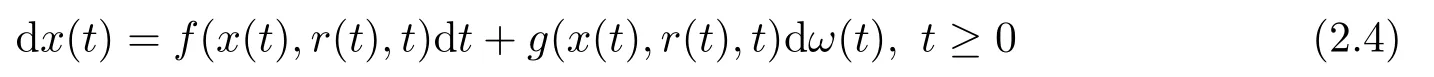
with initial value x(0) = x0∈(Ω;Rn) and r(0) = r0∈S.Under Assumption 2.1，Eq.(2.4) also admits a unique solution x(t) on t ≥0 and the second moment of the solution is finite (see [2]，Theorem 3.13).Denote x(t) = x(t;x0，r0) with initial value (x0，r0) ∈Rn×S.When proving the results in the sequel，we can change the initial data x0and r0appropriately to meet the needs.We now state our stability problems as follows:

1) If the hybrid SDE (2.4) is almost surely exponentially stable，can we infer that the hybrid SDDE (2.1) is also almost surely exponentially stable provided τ is sufficiently small?

2) If 1)has a positive answer，can we find an upper boundsuch that the hybrid SDDE(2.1) is almost surely exponentially stable provided τ ＜

It is therefore natural to assume that the hybrid SDE(2.4)is almost surely exponentially stable.In order to answer the problems 1) and 2)，let C2，1(Rn×R+;R+) be the family of functions V(x，t) : Rn×R+→R+that are continuously twice differentiable in x and once in t.Given any V ∈C2，1(Rn×R+;R+)，define the function LV : Rn×S ×R+→R by LV(x，i，t)=Vt(x，t)+Vx(x，t)f(x，i，t)+trace[gT(x，i，t)Vxx(x，t)g(x，i，t)]，where

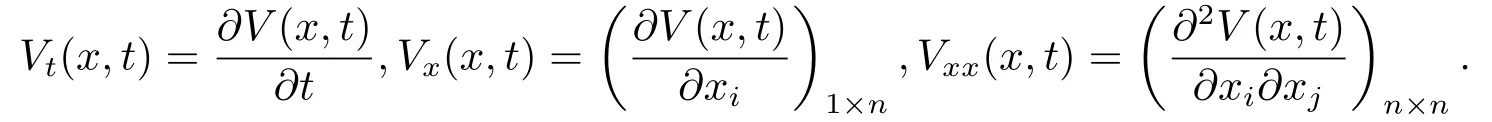
According to Theorem 2.2 in [14]，one can obtain the following result，which will be regard as another assumption in this paper.

Assumption 2.2Assume that there exists a function V ∈C2，1(Rn×R+;R+)，positive constants p，c1，c2，and αi∈R，βi≥0 such that (x，i，t)∈Rn×S×R+，

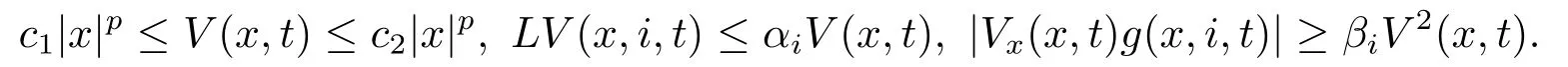
Then

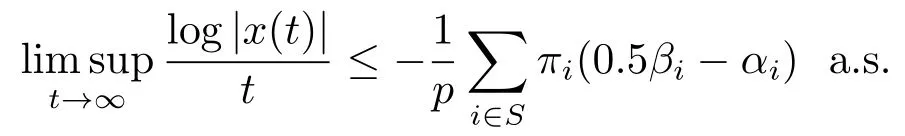
for all x0∈Rn.Ift hen Eq.(2.4) is almost surely exponentially stable.

In order to establish the main results in the next section，the following lemma is useful.Before giving this lemma，we need represent some another denotations first.Let P be the space of all probability measures on the state space S.Then the markov chain r(t) has the rate function I(p) = -where p = (p1，...，pm) ∈P is the probability vector on S and= {u = (u1，...，um) ∈Rm|ui＞0，i = 1，...，m}(see [15，page 136]).It is known that I(p) ≥0 and I(p) = 0 if and only if p = π (see [16]).Then the logarithmic moment-generating function of the Markov process r(t) as follows:

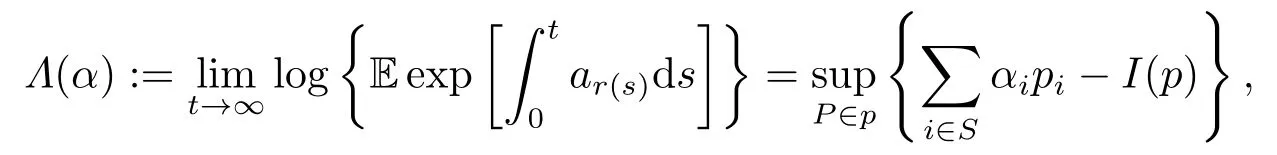
where α=(α1，...，αm)∈Rm.

Similar to prove Theorem 3.1 in[17]，one can obtain the following lemma，which is useful in the subsequent analysis.

Lemma 2.1Let Assumptions 2.1 and 2.2 hold.If Λ(α)＜0，then

That is，the trivial solution of hybrid SDE (2.4) is pth moment exponentially stable.

Note that，in fact，according to Lemma 2.1，one can obtain

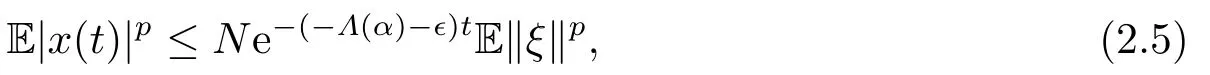
where N =c2/c1and ϵ∈(0，-Λ(α)/2).

3.Main Results

This section will give our main results.We now present positive answers to 1) and 2) in the following theorem.

Theorem 3.1Let Assumptions 2.1 and 2.2 hold.If＞0 and Λ(α)＜0，then there exists a positive constantsatisfying

Remark 3.1The left side of the (3.1) is continuously increasing for τ ≥0 and is equal to ε as τ =0.Based on this point，it can be seen that (3.1) has a unique positive root.

The proof of Theorem 3.1 is complicated，we break it into a number of lemmas.The main purpose of this paper is to tackle the problems 1) and 2)，that is，we should prove Eq.(2.1) is almost surely exponentially stable and find outunder given conditions.In order to achieve such goal，we need estimate the pth (p ＞0) moment of the solution to Eq.(2.1) and Eq.(2.4)，but we can choose the value of positive constant p freely.For convenience，here we choose p=2 to perform our stability analysis.Readers can also choose the other positive constant p to obtain the stability result.

Lemma 3.1Let Assumption 2.1 hold and ξ ∈L2Ft(Ω;C([-τ，0];Rn)).Then，for all t ≥0，

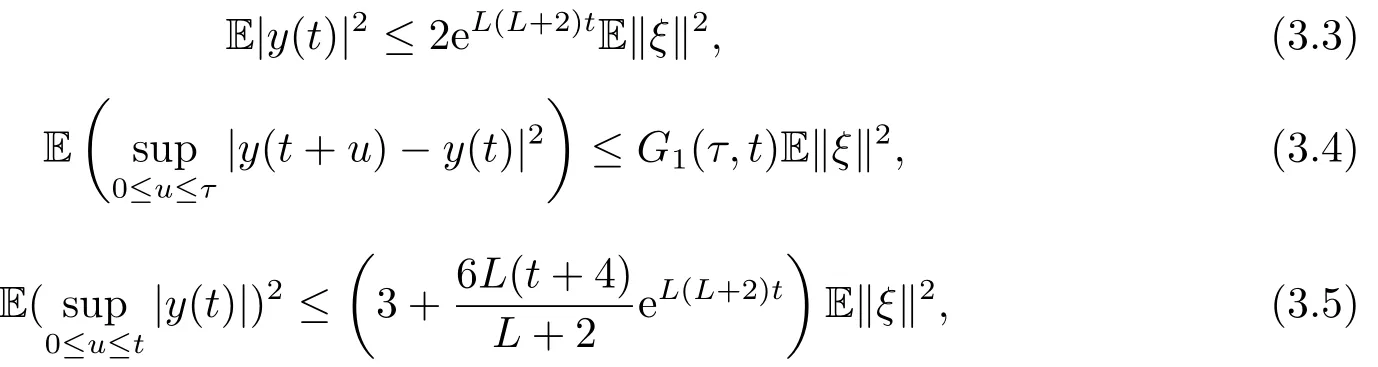
where

ProofApplying the Itˆo formula to |y(t)|2，it follows (2.3) that for t ≥0，

By the Gronwall inequality，one obtains that

implies (3.3) holds.From the Hlder inequality，the Doob martingale inequality，(2.3) and(3.3)，one derives that

Namely，(3.4) holds.Similarly，one can show that

That is，the estimation (3.5) holds.The proof is complete.

Lemma 3.2Let Assumption 2.1 hold and ξ ∈(Ω;C([-τ，0];Rn)).Then，for all t ≥τ，

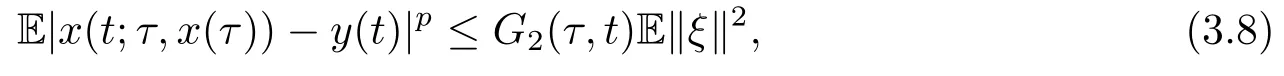
where

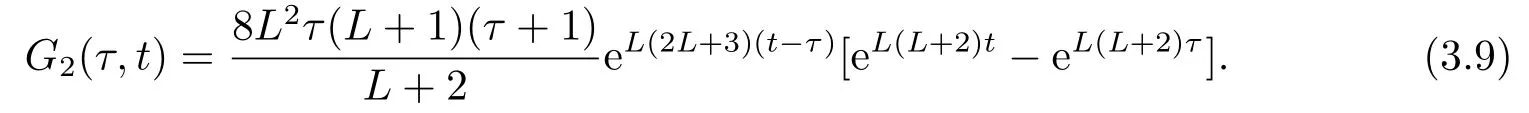
ProofDenote by x(t;τ，y(τ))=x(t).By the Itˆo formula and Assumption 2.1，one can show that for t ≥τ，

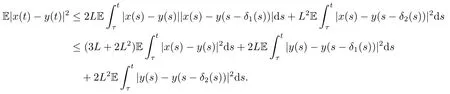
By the Gronwall inequality，one obtains

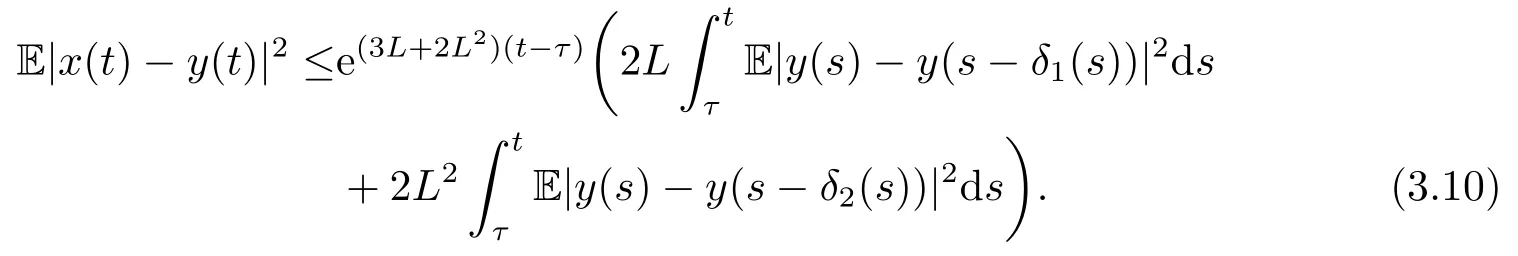
It follows from (3.7) that for s ∈[τ，t] and i=1，2

Substituting (3.11) into (3.10)，one yields E|x(t)-y(t)|2≤G2(τ，t)E‖ξ‖2，where G2(τ，t) has been defined as before.The proof is complete.

We can now prove Theorem 3.1.We will divide the proof into three steps.

Proof of Theorem 3.1Step 1 Fix τ ∈(0，) and ξ ∈Ω;C([-τ，0];Rn)).Denote by x(τ +T;τ，y(τ))=x(τ +T).According to (2.5) and (3.3)，one has

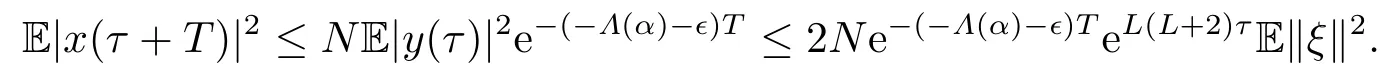
Then，

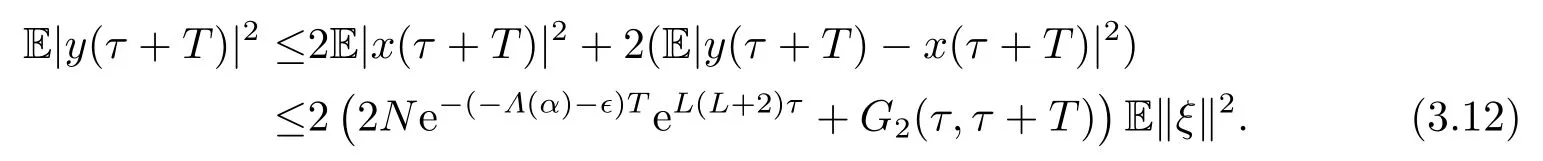
It follows (3.4) and (3.12) that

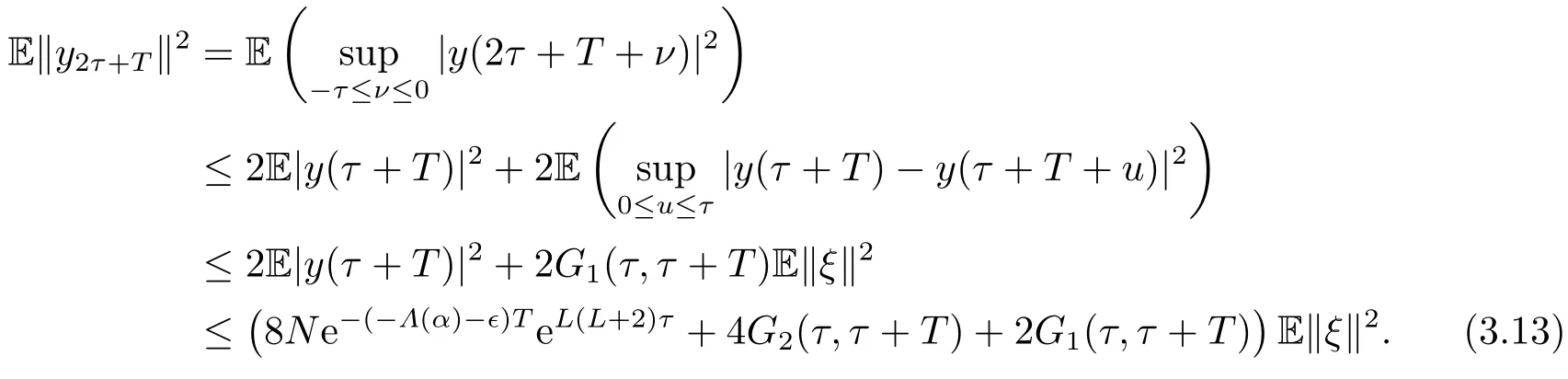
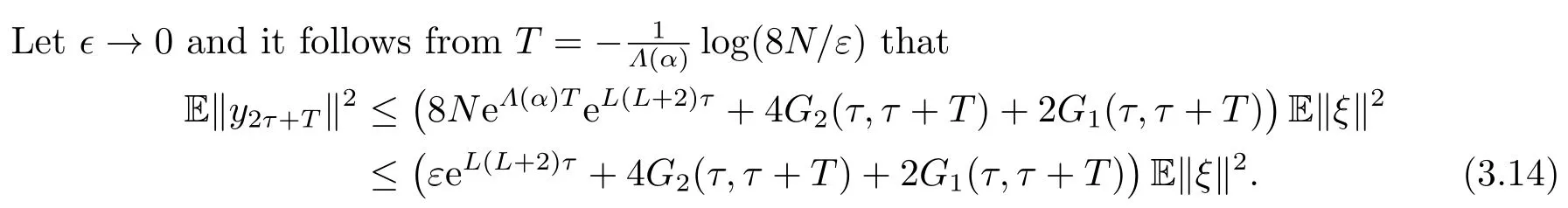
Therefore，for some γ ＞0，one can write

Substituting the above into (3.13)，one can have

Step 2 Consider y(t)(t ≥2τ +T) as the solution of Eq.(2.1) with the initial value y2τ+Tat t=2τ +T.By Step 1 and (3.15)，one gains

By induction and repeat this procedure，for all k =1，2，...，one gains

And when k =0，it is obvious that E‖y0‖≤E‖ξ‖2.Therefore，(3.16)holds for all k =0，1，....According to (3.5) and (3.16)，it follows

for all k =0，1，...，where

Step 3 It follows from (3.17) that for all k ≥0 and ∀ε1＞0

From the Borel-cantelli lemma，one can get that for almost all ω ∈Ω，there exists an integer k0=k0(ω) satisfying

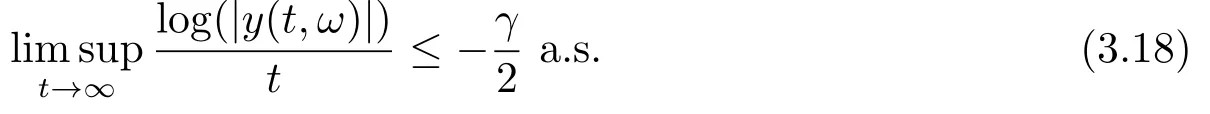
The proof is complete.