A Partly Smoothing-Regularization Method for Mathematical Programs with Vanishing Constraints

DONG Yanfeng(董艳凤)，CHU Dejian(初德建) HU Linyu(胡林玉)，HU Qingjie(胡清洁)1，2，

(1.Guangxi Key Laboratory of Automatic Detecting Technology and Instruments，Guilin 541004，China; 2.Guangxi Colleges and Universities Key Laboratory of Data Analysis and Computation，Guilin 541004，China; 3.School of Mathematics and Computing Science，Guilin University of Electronic Technology，Guilin 541004，China)

Abstract: In this paper，we consider the mathematical programs with vanishing constraints (MPVC).We present a pseudo Huber function based smoothing-regularization method for this problem，which only makes the part ones of the vanishing constraints be smoothed.For the new smoothed problem，we show that the Mangasarian-Fromovitz constraints qualification (MFCQ) holds under some conditions.We also analyze the convergence behavior of the smoothing-regularization method，i.e.，an accumulation point of the stationary points sequence for the smoothing-regularization problem is a T-stationary point，and obtain some sufficient conditions such that an accumulation point of the stationary points sequence for the smoothing-regularization problem is M-or S-stationarity，respectively.Finally，some preliminary numerical results show that the proposed method may be promising.

Key words: Mathematical program with vanishing constraint; T-stationarity; Mstationarity; S-stationarity; Numerical result

1.Introduction

We consider a mathematical program with vanishing constraints as follows:

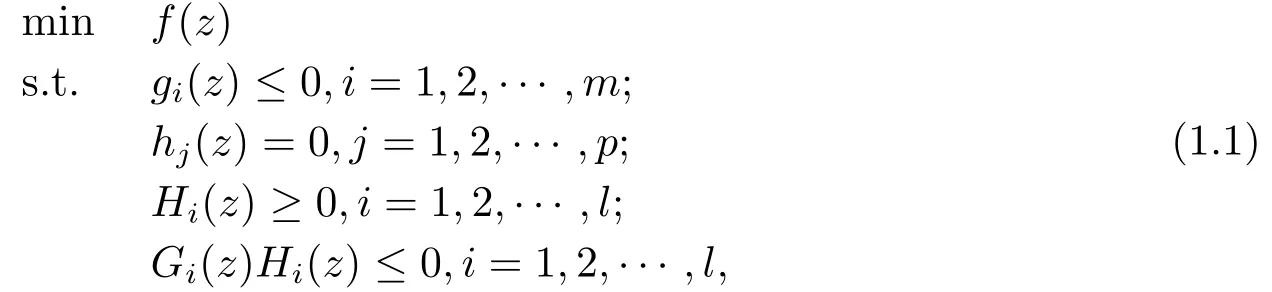
where f : Rn→R，g : Rn→Rm，h : Rn→Rpand H : Rn→Rlare all twice continuously differentiable functions.

The MPVC was firstly introduced to the optimization community in [1].It plays an important role in some fields such as topology optimization design problems in mechanical structures[1]，a robot path-finding problem with logic communication constraints in robot motion planning[19]，scheduling problems with disjoint feasible regions in power generation dispatch[20]and mixed-integer nonlinear optimal control problems[21-22].The major difficulty in solving the problem (1.1) is that it does not satisfy the standard constraint qualification at some feasible point so that the standard optimization methods are likely to fail for this problem.The problem is closely related to the mathematical programs with equilibrium constraints (MPEC).Theoretically，it is possible to formulate an MPVC as an MPEC and vice versa.However，these formulations have certain disadvantages like the introduction of additional solutions[1]or the violation of MPEC type constraint qualifications[13]，which cause some troubles when the MPEC formulation is solved by some classical algorithms.Moreover，the dimension of the MPEC formulation is larger than the original MPVC.These observations motivate us to consider it as an independent class of interesting mathematical programs.

The MPVC has attracted much attention in the recent years.Some theoretical properties and numerical tricks for MPVC can be found in [2-16].Among these numerical methods，the smoothing method is one of the important methods.Recently，Kanzow et al.[2]have proposed a smoothing-regularization approach to mathematical programs with vanishing constraints.Their basic idea is to reformulate the characteristic constraints of the MPVC via a nonsmooth function and to regularize the feasible set with the aid of a certain smoothing parameter.The convergence behavior of a sequence of stationary points of the smoothed and regularized problems has been investigated.

In this paper，based on the pseudo Huber function，a new smoothing-regularization method for the mathematical programs with vanishing constraints is presented.Different from the one in [2]，only the part ones of the vanishing constraints are smoothed.Moreover，for the new smoothed problem，we show that the MFCQ holds under some conditions.We prove that an accumulation point of the stationary points sequence for the smoothingregularization problem is a T-stationary point，and investigate some sufficient conditions such that an accumulation point of the stationary points sequence for the smoothed problem is Mor S-stationarity.Finally，some numerical results are given.

The rest of the paper is organized as follows: In Section 2，we review some concepts of nonlinear programming and MPVC，and present the new smoothing-regularization method for (1.1).In Section 3，we give the analysis of the convergence property.In Section 4，some preliminary numerical results are shown.

For convenience of discussion，some notations to be used in this paper are given.The i-th component of G will be denoted by Gi，X denote the feasible set of the problem (1.1).For a function g :Rn→Rmand a given vector α ∈Rn，we use

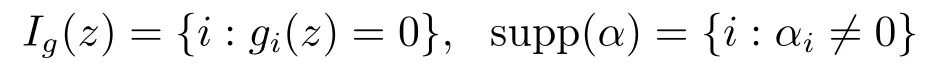
to denote the active index set of g at z ∈Rnand the support of α，respectively.

2.Preliminaries

Firstly，we will introduce some definitions of nonlinear programming.It is an optimization problem of the form

where f :Rn→R，g :Rn→Rm，h:Rn→Rpare all continuously differentiable functions.

We denote the feasible set of problem (2.1) by F.

Definition 2.1A point∈F is called a stationary point for(2.1)if there are multipliers λ，µsuch that(，λ，µ)is a KKT point of(2.1)，i.e.，the multipliers satisfy λ ∈andµ∈Rpwith λigi()=0 for all i=1，2，··· ，m，and

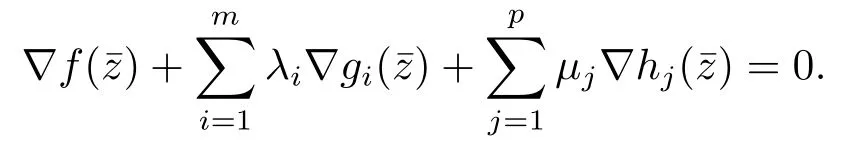
Definition 2.2A feasible pointfor (2.1) is said to satisfy the MFCQ if the gradients{∇hi()|i=1，2，··· ，p} are linearly independent and there is a d ∈Rnsuch that

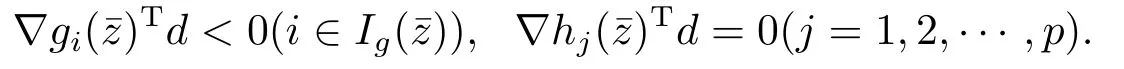
Definition 2.3A finite set of vectors {ai|i ∈I1}∪{bi|i ∈I2} is said to be positive linearly dependent if there exists (α，β)0 such that

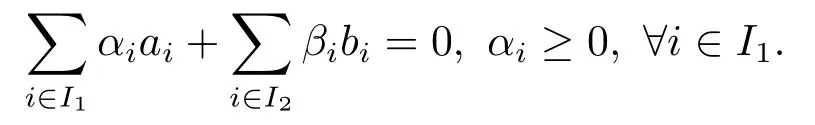
If the above system only has a solution (α，β)=0，we say that these vectors are positive linearly independent.

By using Motzkin’s theorem of the alternatives in [18]，we can obtain the following property.

Lemma 2.1A point∈F satisfies the MFCQ if and only if the gradients

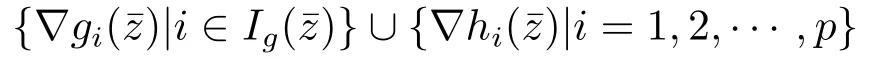
are positive-linearly independent.

Now，we give the following sets of active constraints for an arbitrary∈X for the problem (1.1):

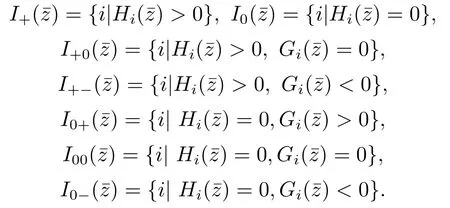
Definition 2.4[23]A feasible pointfor (1.1) satisfies the MPVC-MFCQ if and only if

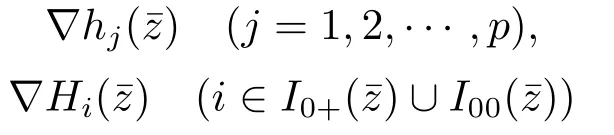
are linearly independent and there exists a vector d ∈Rnsuch that

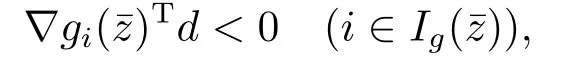
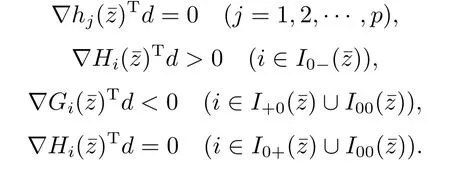
Definition 2.5[23]Letbe a feasible point for the problem (1.1)，then.

Similar to Lemma 2.1，we can also deduce that the following result holds.

Lemma 2.2A point∈X satisfies the MPVC-MFCQ if and only if the gradients

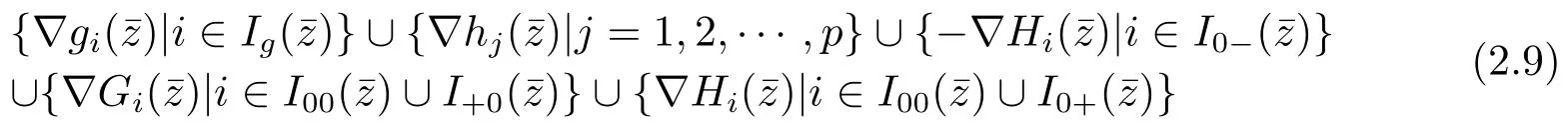
are positive-linearly independent.

In the next disscusion of this section，we shall propose a new smoothing-regularization method for the problem (1.1).

Firstly，it is easy to see that b ≥0，ab ≤0 is equivalent to b ≥0，a+b ≤|a-b|.Hence，we can obtain a smooth approximation to the part vanishing constraints by constructing a smoothing approximate expression of the absolute value function |·|.

To achieve such a goal，the first order methods usually replace the absolute value function|·| by the following Huber function[25]，where

where ε ＞0.The smaller the parameter ε of the Huber function is，the better the function approximates the absolute value function.Obviously，the Huber function is only first-order differentiable，thus this approximation approach is not applicable to second-order methods.Fortunately，the pseudo Huber function which has derivatives of all degrees[26]is a smooth version of the Huber function.This function parameterized with ε ＞0 is

Hence，φε(·) can be used to construct a smooth approximation to the function |·|.

Based on the above discussions，it is clear that the MPVC (1.1) can be approximated as a smoothed optimization problem:

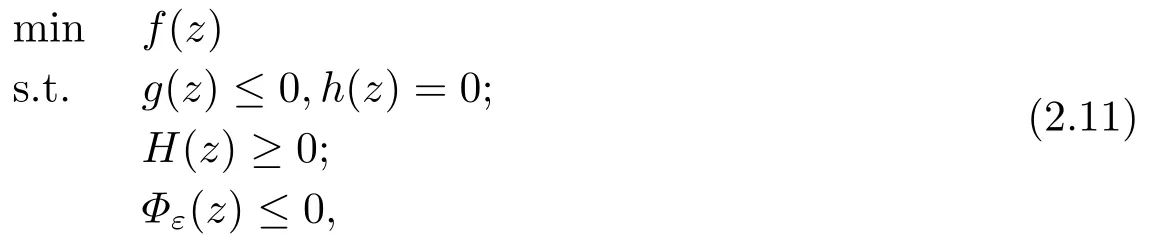
where

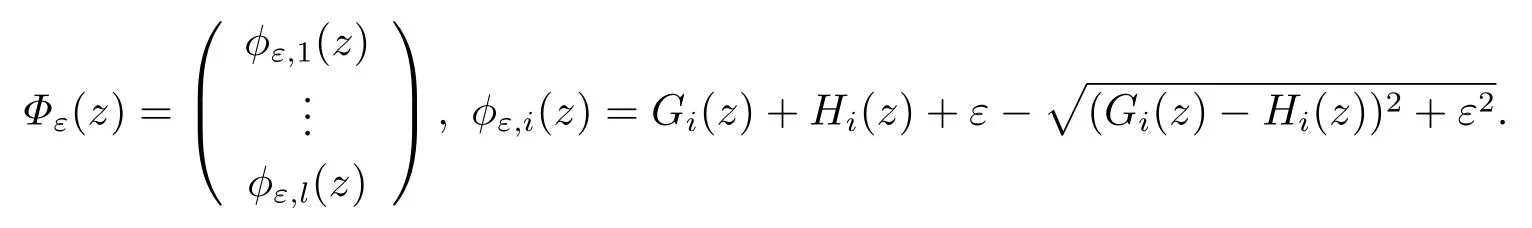
We denote the feasible set of (2.11) by Xε.

3.Convergence Analysis

In this section，we will consider the limiting behavior of stationary points sequence of the new smoothing-regularization problem.Firstly，we discuss the constraint qualification of(2.11).

For convenience of discussion，we give the following notations:

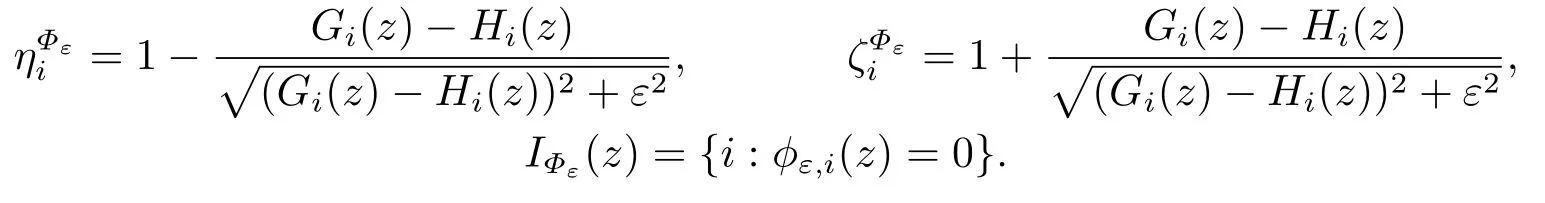
For the subsequent analysis，the following lemma is necessary.Its proof is elementary，and is omitted.

Lemma 3.1Letbe feasible point of (1.1).The following relationships hold:

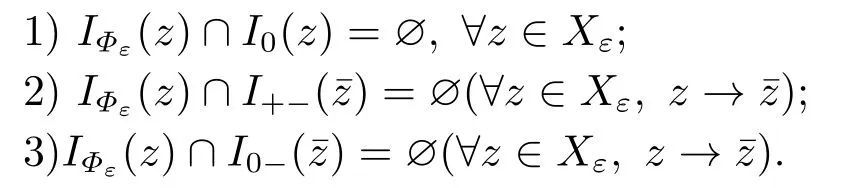
The following theorem shows that the Mangasarian-Fromovitz constraints qualification for the problem (2.11) holds under some conditions.

Theorem 3.1Letbe feasible for (1.1) such that the MPVC-MFCQ is satisfied at.Then there exit a neighborhood U()ofand a sufficiently small＞0 such that the problem(2.11) satisfies the standard MFCQ at any point z ∈U()∩Xεfor any ε ∈(0，).

ProofSince g，h，G，H are all continuous，there exist a neighborhood U1() and a positive constantsuch that for any ε ∈(0，1) and any point z ∈U1()∩Xε，we have

In each of the two wings of the castle there was astaircase which led to a place below the entrance, from whence thereis access to a low, vaulted cellar

Noting that the MPVC-MFCQ holds，we have the gradients

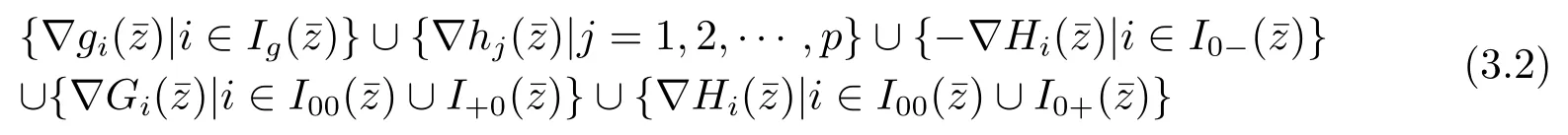
are positive-linearly independent by Lemma 2.2.Take into account that

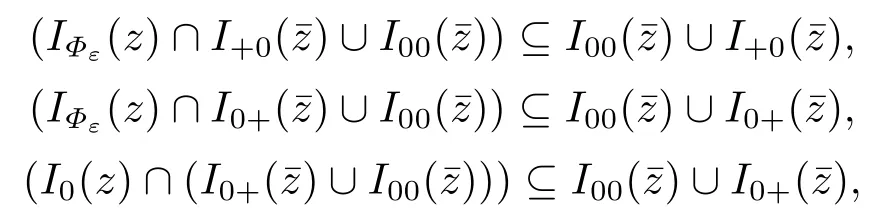
and

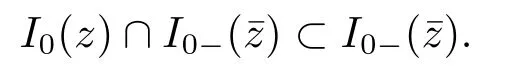
It’s known that Hi(z)＞0，Gi(z)≈0 for all i ∈I+0() as well as Hi(z)≈0，Gi(z)＞0 for all i ∈I0+() if z is close to.Similar to the proof of Proposition 2.2 in [17]，utilizing Lemma 3.1，we know that there is a neighborhood U2() and an2＞0 such that the set of vectors

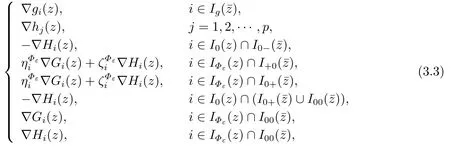
are positive-linearly independent for all z ∈U2()∩Xεand ε ∈(0，2).

We now claim that the standard MFCQ holds for the problem (2.11) if z ∈U()∩Xε，where U() = U1()∩U2() and ε ∈(0，)，= min{1，2}.To this end，take an arbitrary z ∈U()∩Xε.In view of Lemma 2.1，we have to show that

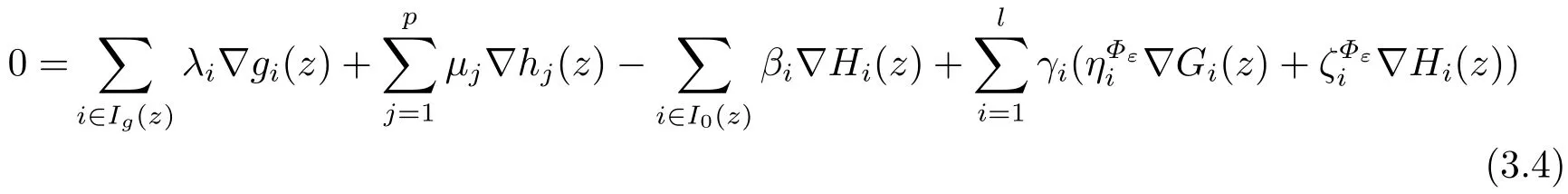
with µi∈Rpand λ，β，γ ≥0 holds with the null vector only.Taking into account Lemma 3.1，we rewrite (3.4) as

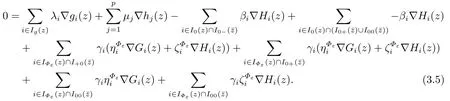
Applying the positive linear independence of vectors from (3.3) to (3.5)，in view of (3.1)，one gets

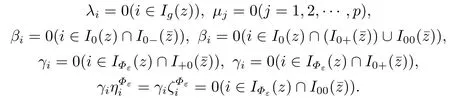
Theorem 3.2Let {εk} be a positive sequence which is convergent to zero.Suppose that {zk} is a sequence of stationary points of the problem (2.11) with ε = εk.Ifis an accumulation point of the sequence {zk} such that the MPVC-MFCQ holds at，thenis a T-stationary point of the problem (1.1).

ProofIt follows from Theorem 3.1 that there exist Lagrange multiplier vectors λk，µk，γksuch that

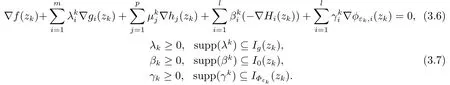
From (3.6)，we have

In view of the definitions ofand，we can define

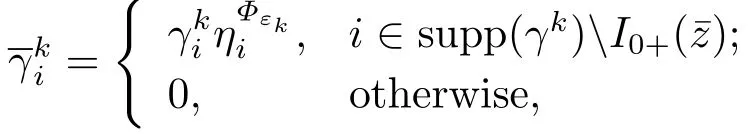
and

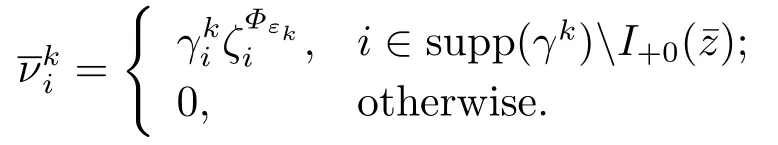
Note that the definitions ofand.(3.6) can be rewritten as

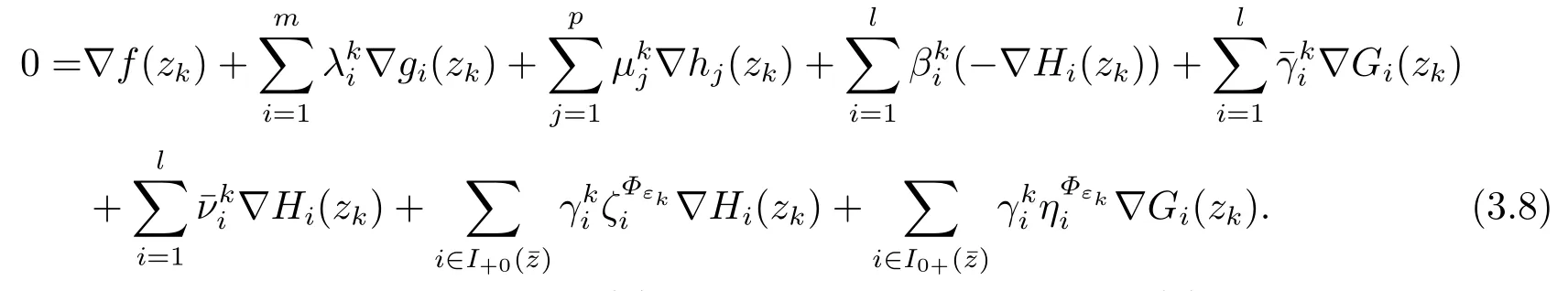
We now prove that the sequenceis bounded.

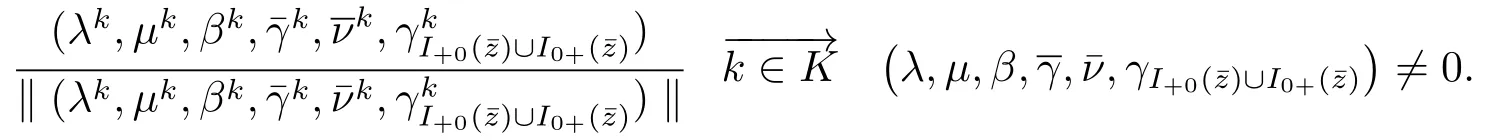
Combined with (3.8)，it yields

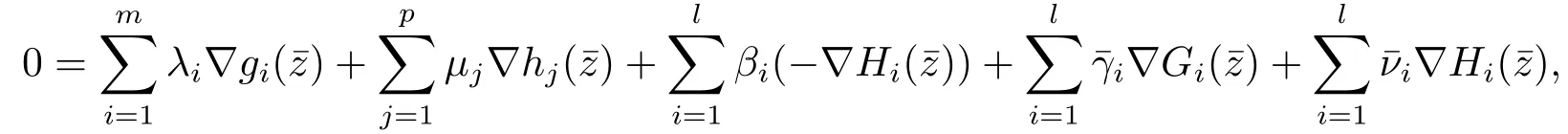
i.e.，

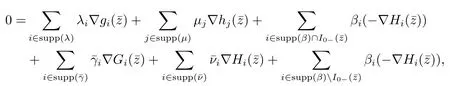
where λ ≥0 and for all k ∈K large enough，

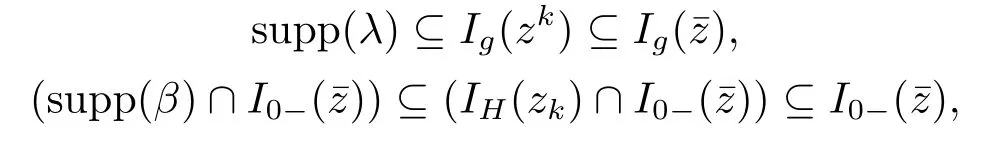
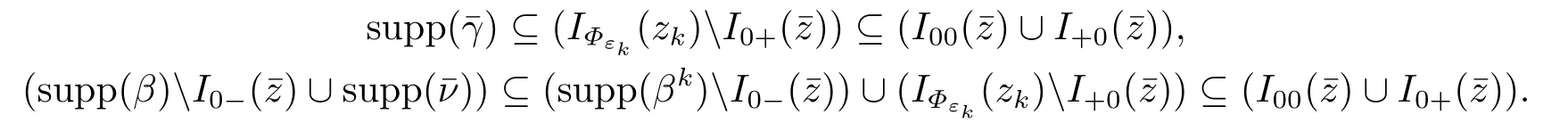
The following object is to prove that (λ，µ，β，)0.

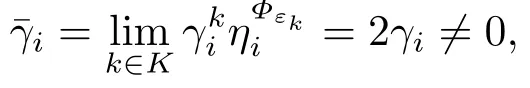
which contradicts the assumption=0.

By Lemma 2.2，we know that (λ，µ，β，)0 contradicts the fact that the MPVCMFCQ holds at.Thus，we have proved that the sequenceis bounded.

Without loss of generality，we now suppose that the sequence

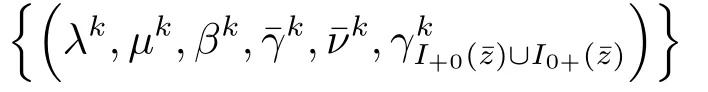
Since f，g，h，G and H are continuously differentiable，we have

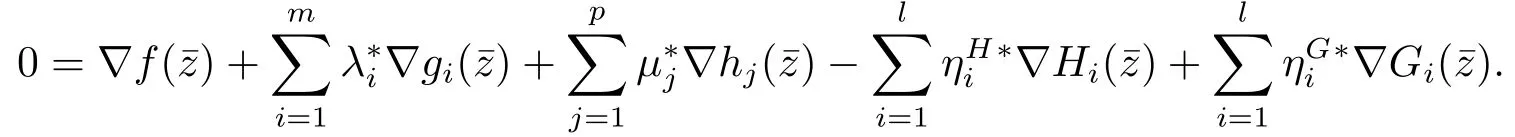
Finally，from the definitions ofandLemma 3.1 and Definition 2.5，it follows thatis the T-stationary of the original MPVC (1.1).

Next，we will analyse the sufficient conditions on M-stationarity.

Theorem 3.3Let {εk} be a positive sequence which is convergent to zero.Suppose that zkis a stationary point of the problem (2.11) with ε=εk.Ifis an accumulation point of the sequence{zk}such that the MPVC-MFCQ holds atand max{Hi(zk)，εk}=o(Gi(zk))or max{Gi(zk)，εk}=o(Hi(zk)) for all i ∈I00()∩IΦε(zk)，thenis a M-stationary point of the problem (1.1).

ProofFrom Theorem 3.2，we can obtain thatis a T-stationary point of the problem(1.1).In order to show thatis an M-stationary point of the problem (1.1)，we only need to prove that= 0 for i ∈I00().If i ∈I00()∩IΦε(zk)，then Gi(zk)+Hi(zk)+εk=Hence，

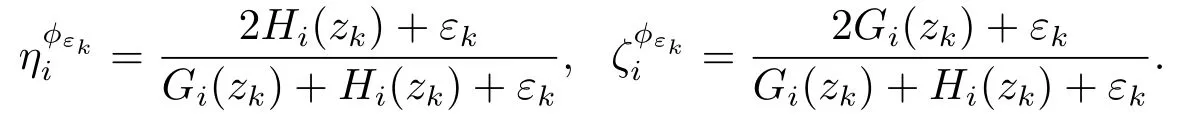
In view of that max{Hi(zk)，εk} = o(Gi(zk)) or max{Gi(zk)，εk} = o(Hi(zk)) for all i ∈I00()∩IΦε(zk)，one gets

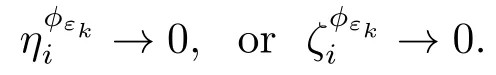
From the proof of Theorem 3.1 and= 2，we can obtain that {γk} is bounded.Thus，for all i ∈I00()∩IΦε(zk).This implies thatis an M-stationary point of the problem (1.1).

In order to obtain the strong stationarity of the accumulation point，we give the following assumption.

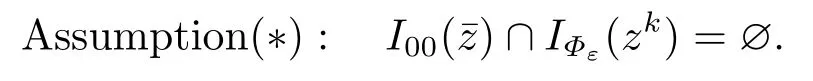
This assumption is similar to the asymptotic weak nondegeneracy assumption which was defined for the MPEC[10].Combining it and the MPVC-MFCQ，it is strong enough to guarantee S-stationarity of a accumulation point of the sequence generated by the smoothingregularization method.

Theorem 3.4Let {εk} be a positive sequence which is convergent to zero.Suppose that zkis a stationary point of the problem (2.11) with ε=εk.Ifis an accumulation point of the sequence {zk} such that the MPVC-MFCQ and Assumption (*) hold at，thenis a S-stationary point of the problem (1.1).

ProofTo prove the above result，we only need to prove that= 0，≥0 for i ∈I00().Obviously，Assumption (*) implies that supp(*)∩I00() = ∅and supp(*)∩I00()=∅.Hence，is a S-stationary point of the problem (1.1).

4.Numerical Results

In this section，we report the numerical results about the proposed approach.We also compare our method with the smoothing regularization approach which was proposed by Kanzow et al.[2]In the numerical implementation，we use the build-in MATLAB R2012b function fmincon which is a publicly available software to solve (2.11).To perform numerical test，we use the two test problems considered in the thesis of Hoheisel[23].Our numerical experiments are divided into two sections.

In the first section of numerical experiments，we consider the following example:

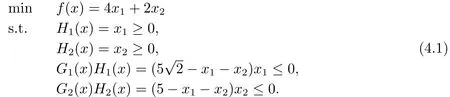
This model is based on the mechanical structure topology optimization problem，where x1，x2≥0 represents the cross-sectional area of different truss bars，respectively.A comprehensive analysis of the variables in the mechanical structure model can be found in [24].If the problem (4.1) is considered as a pure mathematical model，then it can be proved that x*=(0，0)T，x+=(0，5)Tare all strongly stationary points[2].Obviously，the point x*is the global minimizer of the problem.Although，from the view of the practical applications，the point of the cross-sectional area of the bar being zero is no practical significance，in our test，we only consider the point x+，since it will be interesting whether these methods can find it.

Firstly，we make a test of different starting points for two problem formulations which are corresponding to our method and the one of Kanzow et al.During the numerical experiment，we select the staring points x1，x2∈{-5，-4，··· ，20}，and select ε = 0.001.The following Fig.4.1 and Fig.4.2 illustrate their convergence behavior.In the two figures，we use “*”to indicate the termination point approximating to x*= (0，0)T，and “+” to indicate the termination point approximating to x+= (0，5)T.From the two figures，we can see that the termination points of the two methods are different for the different starting points，from the view of practical significance，the proposed method is better than the one of Kanzow et al.

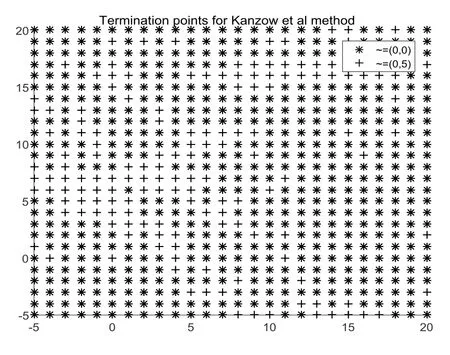
Fig.4.1 Termination points for the method of Kanzow et al.

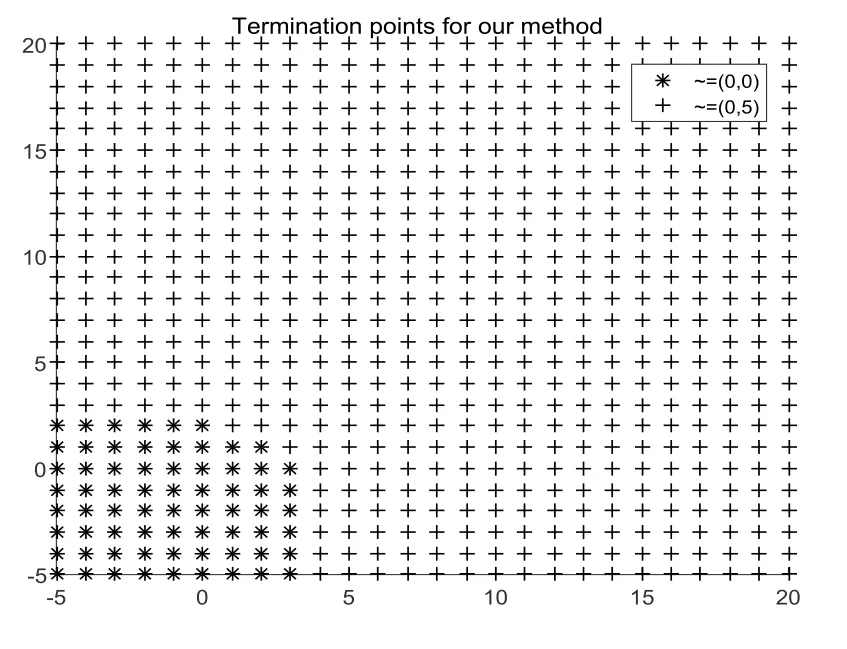
Fig.4.2 Termination points for our method

Secondly，we next investigate the influence of the choice of ε for two problem formulations.For this purpose，we fix the starting point x0=(0.5，0.5)T.The results are displayed in Tab.4.1 and Tab.4.2.From the two tables，we can see that the iteration numbers of our method is smaller than the ones of the method of Kanzow et al.Furthermore，the accuracy of our method is higher than the ones of the method of Kanzow et al.

Tab.4.1 Results of the method of Kanzow et al.for different values of ε

Tab.4.2 Results of our method for different values of ε

In the second section of numerical experiments，we consider the following practical problem，i.e.，ten-bar truss model:

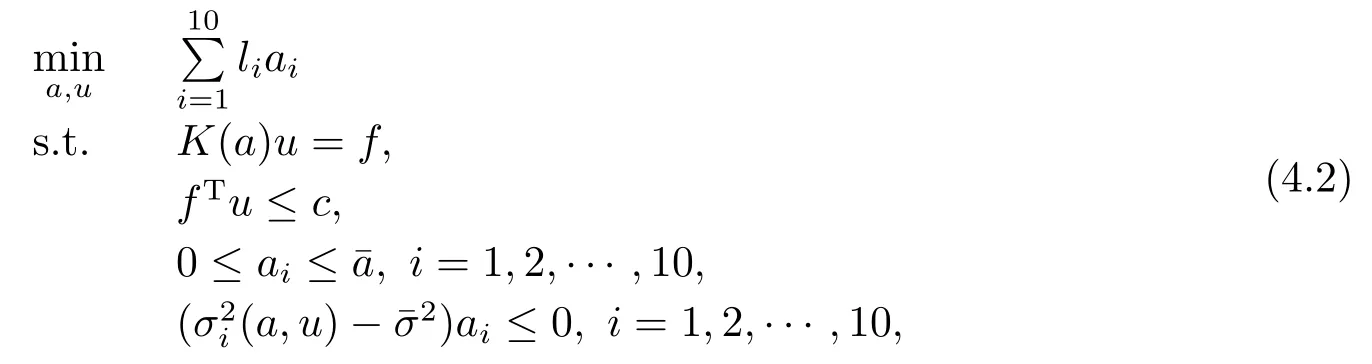
where f is the external force applying at the bottom right hand nodal point which pulls vertically to the ground with ‖f‖ = 1，liis the length of the potential bar，aiis the corresponding cross-sectional area，u ∈R8is a vector of the nodal displacements points，is a global stiffness matrix，σi(a，u) == 1，2，··· ，10 denotes the stress of the i-th potential bar.

During our numerical experiment，we choose that li=1，i ∈{1，3，5，6，8，10}，li={2，4，7，9}，c = 10，= 100，= 1，Young’s modulus E = 1.The vector γiis contained in Tab.4.3.We choose ε=0.001 and the starting point(a，u)T=(0，0)T∈R18.

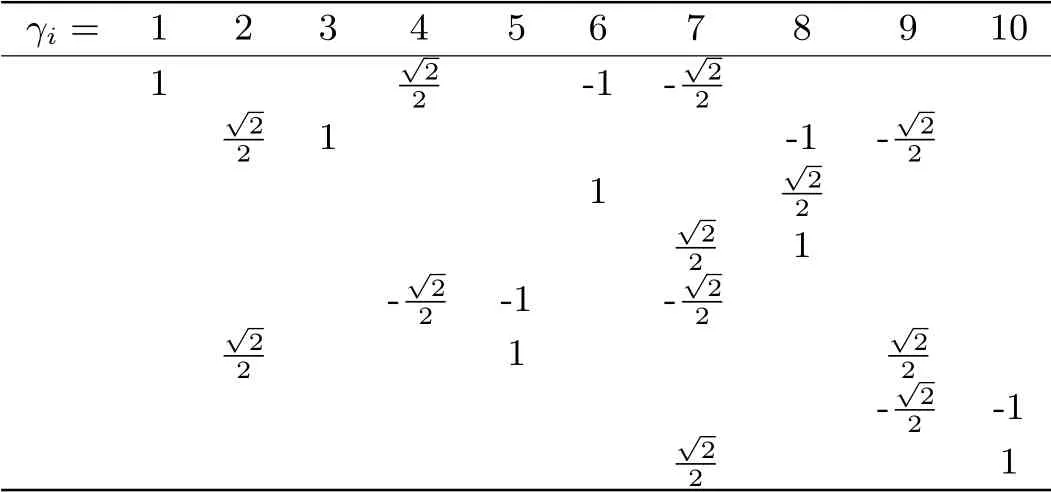
Tab.4.3 Vectors γi for ten-bar truss

For comparison，we show the full data containing the stress values in Tab.4.4 and Tab.4.5.From the two tables，we can see that the resulting structures generated by the two methods consist of 5 bars，and are all same as the ones in [23].Our method requires 42 iterations to terminate at the point (a*，u*)，but the method of Kanzows et al.requires 142 iterations.

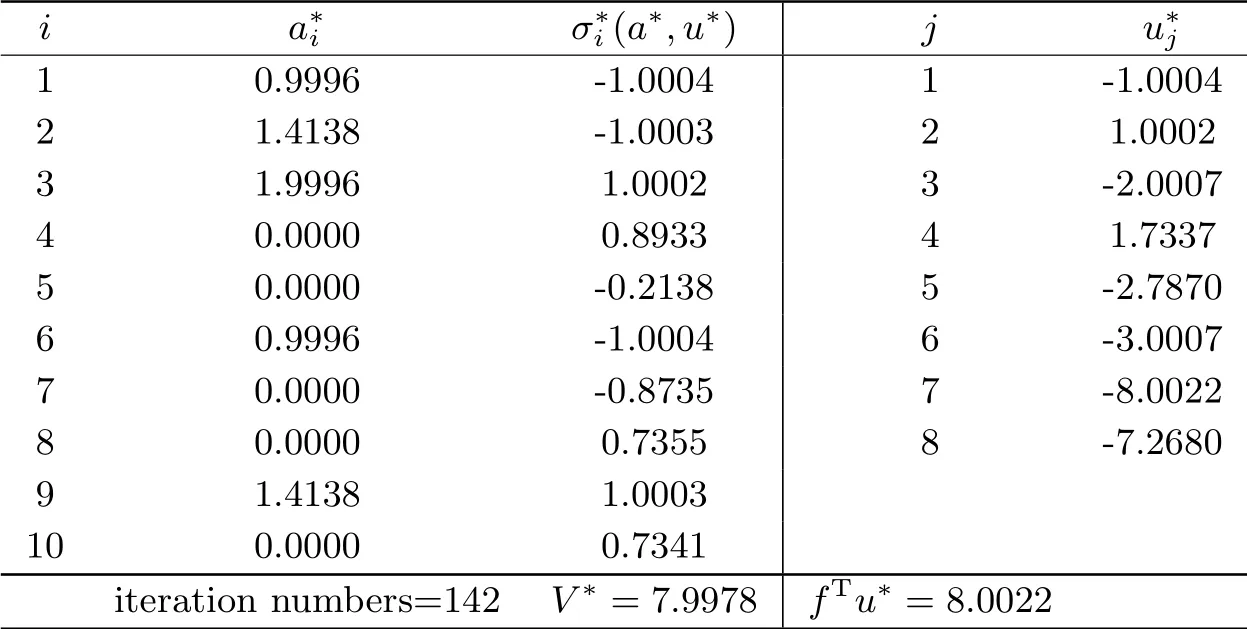
Tab.4.4 Results of the method of Kanzow et al.for ten-bar truss problem

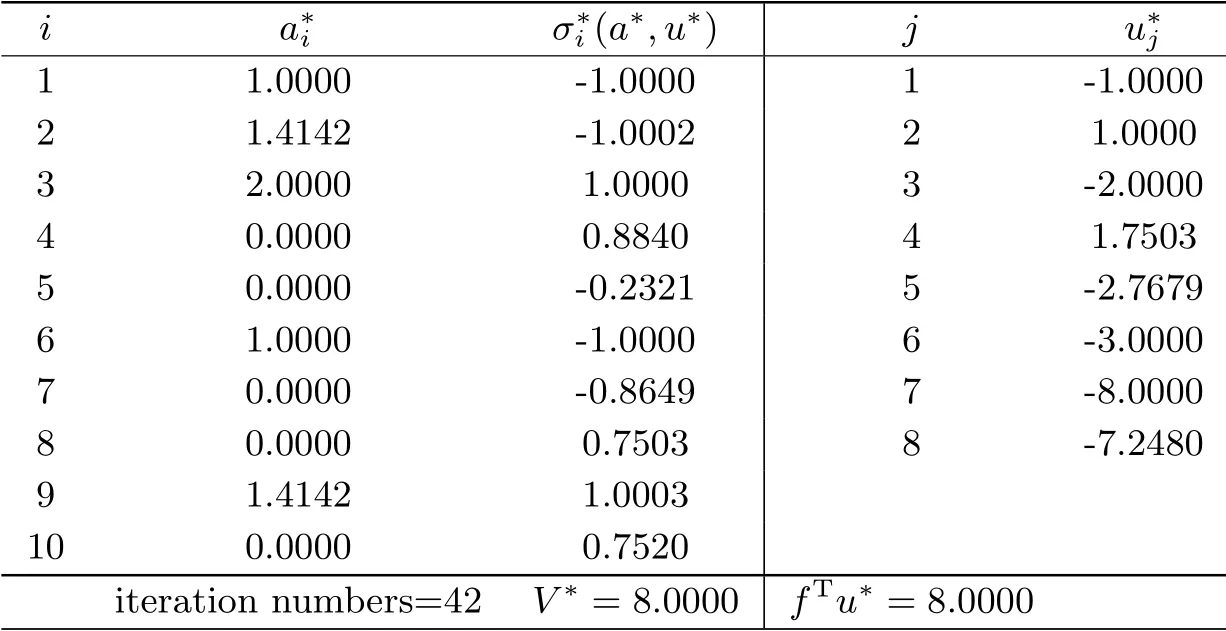
Tab.4.5 Results of our method for ten-bar truss problem