一类具有切换拓扑和随机故障影响的集群演化模型分析

乔正阳，刘易成

(国防科技大学数学系，湖南 长沙410073)

1.引言

我们知道，多智能系统在生态学，物理学，社会学以及人工智能等学科中应用广泛.这类系统的显著特点是通过分离独立的个体间的信息交互，系统能涌现出预先设计的集群特征.Cucker和Smale在文[4-5]中给出了一类描述多智能体系统演化的模型(C-S模型)，并且刻画了该模型的群体演化行为.随后，很多学者研究了各种变形的C-S模型，进一步刻画该模型的复杂群体演化行为，其中包括时滞影响下的C-S模型和不同拓扑结构的C-S模型等.在文[14]中，SHEN研究了具有等级结构的C-S模型.近年来，LI和XUE 在文[12]中研究了具有根结点领导的C-S模型.同时考虑了切换拓扑的影响情形，这类拓扑结构比等级结构更具一般性.在文[8]中DONG和QIU研究了一般拓扑结构下的C-S 模型的群体演化行为，该文对拓扑结构的要求仅需要拓扑交换图存在一个生成树即可.随后Cucker和DONG在文[2]中研究了一般情形下带有切换拓扑的C-S 模型.由于多智能体系统中个体之间相互连接的拓扑结构往往是不断变化的，在文[1]中，作者发现鸽群中个体之间采用间歇性交互机制，并不是每时每刻的都进行组内信息传输.因此具有切换拓扑的C-S模型具有很强的实际意义.

同时，多智能系统中的个体之间的连接会受到外界因素的干扰，导致相互作用发生改变，甚至连接失败.带有随机故障的C-S模型能更好地描述这种影响.在文[6-7] 中，Dalmao和Mordecki研究了随机故障下具有等级结构的C-S模型.随后RU，LI和XUE在文[13]中研究了随机故障下具有根结构的C-S模型.Dalmao和RU等人也考虑了具有固定故障概率的随机故障C-S模型，这里故障概率是独立同分布的伯努利随机变量.近年来，HE和MU在文[10]中考虑了具有随机故障的一般C-S模型，其中故障概率并不一定是独立的，这里故障概率不再用伯努利随机变量描述，而是利用齐次Markov链描述.本文以Cucker和DONG在文[2]中带有切换拓扑的C-S模型为基础，结合文[10]中的方法，对带有切换拓扑和随机故障影响的C-S模型的集群演化行为进行了研究，获得了系统几乎必然发生集群演化行为的充分条件.

本文的结构如下: 第2节将介绍有向图以及切换系统的基本概念，描述具有切换拓扑和随机故障影响的C-S模型，给出关于故障概率和切换方式的假设条件以及相关引理结论; 第3 节给出了具有切换拓扑和随机故障影响的C-S模型的主要结果和证明过程.由于拓扑结构是可切换的，我们需要一种新的方法估计带有切换拓扑和随机故障的拓扑交互图的遍历系数，进而证明系统几乎必然发生集群演化行为.最后，通过数值仿真方法，获得了故障概率和切换间隔增大时，系统的集群演化行为的变化特点.

2.预备知识

本文利用有向图描述集群中个体之间的相互作用拓扑.设G = (V，E)是由顶点集V ={1，2，···n}和边集E ⊂V ×V构成.如果(j，i) ∈E表示个体i可以直接从个体j处接收信息，此时称个体j是个体i的一个邻接点.个体i的邻接集记为Ni= {j ∈V : (j，i) ∈E}.若(i，i) ∈E，则图G在点i处有一个自循环.对于图G的邻接矩阵A = (aij)n×n，则当(j，i) ∈E时，有aij＞0，否则aij= 0.称边序列(i0，i1)，(i1，i2)，··· ，(ik-1，ik)为从i0到ik的一条路径.如果存在一条从i到j路径，则称顶点j关于顶点i是可达的.在有向图中，如果存在一个顶点(称为根结点)可以到达图中任何其他顶点，则称图是有根的.

集群个体之间的交互方式表示为有向图，它可以在一个有限的模式集P = {1，2···p}中切换.切换方式由函数σ : [0，∞) →P表示，每一时刻σ对应着一个有向图，且σ为右连续的分段函数.σ的不连续点集组成一个可数序列，其中每一个点表示切换时刻.不失一般性我们将切换时刻序列记为{ts}，其中t0= 0.图Gσ(t)= (V，Eσ(t))表示t时刻的交互图.表示t时刻图Gσ(t)中顶点i的邻接集.时间区间t ∈[t1，t2)上的联合图定义为

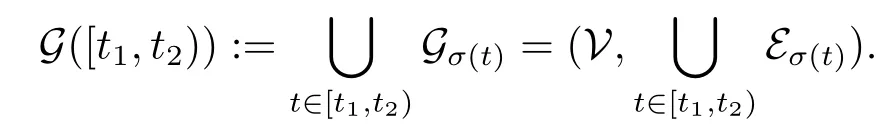
对于矩阵A=(aij)n×n，如果所有aij≥0且行和满足则称矩阵A为随机矩阵.如果对任意的i和j都存在k，使得aik＞0和ajk＞0，则称矩阵A为不规则的.矩阵A的遍历系数定义为

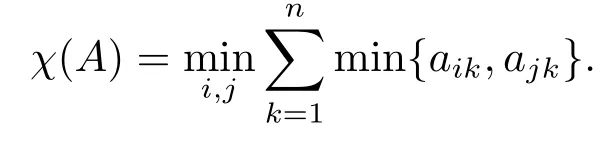
由此可知，χ(A)＞0当且仅当A是不规则矩阵.如果A是随机矩阵，则χ(A)∈[0，1].

此外对于任意矩阵A = (aij)n×n，B = (bij)n×n，我们定义A ≥B表示对任意的i，j有aij≥bij.

考虑n个个体组成的集群系统，集群拓扑结构对应的交互图为G，集群演化过程在离散时刻t ∈N满足如下：

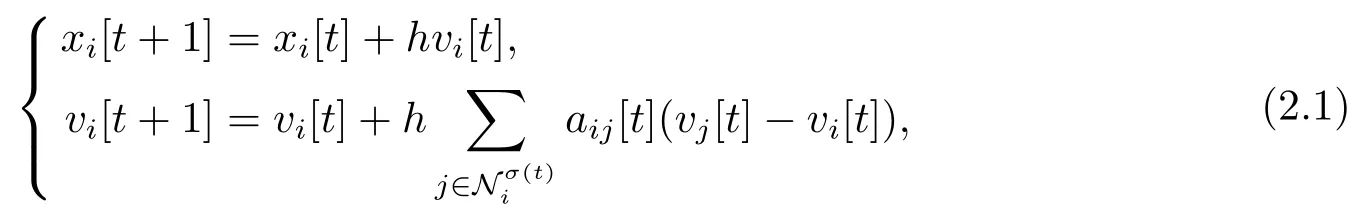
其中h ＞0表示时间步长，1 ≤i ≤n，xi[t]和vi[t] ∈Rm(m ≥1)表示个体i在th时刻的位置和速度.表示个体i在th时刻的邻接集.Gσ[t]= (V，Eσ[t]))表示th时刻的相互作用拓扑图.如果(j，i) ∈Eσ[t])当且仅当j ∈此外假定i ∈我们考虑随机故障的影响，引入影响函数

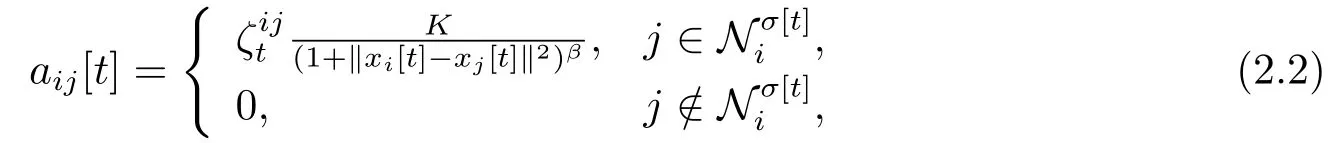
假设2.1假设当t ∈N，j ∈时，随机事件满足：

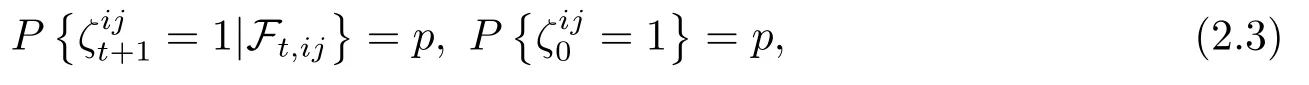
其中Ft，ij表示一个双状态的齐次马尔可夫链，状态空间为{0，1}.Ft，ij包含从初始时刻到t时刻的随机事件的所有信息，p表示t时刻未发生故障概率，p=1-λ.

由上述假设可知

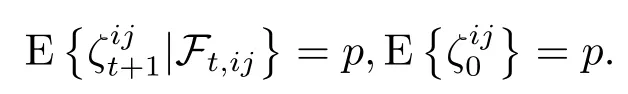
接下来，给出随机故障情况下的集群定义.本文中‖·‖均为2-范数.定义

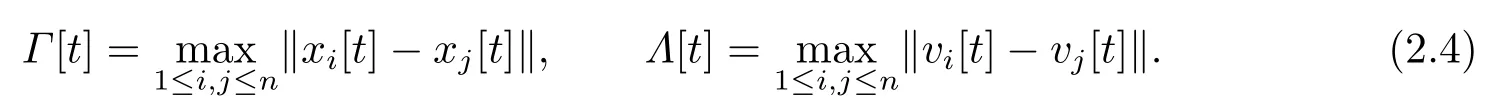
定义2.1如果系统(2.1)-(2.2)的解几乎必然满足如下条件

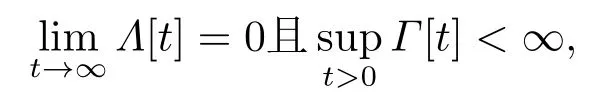
则称系统(2.1)-(2.2)发生集群演化行为.

A[t] = (aij[t])n×n表示系统(2.1)-(2.2)的邻接矩阵.令L[t] = D[t]-A[t]为矩阵A[t]对应的Laplacian矩阵，D[t] = diag(d1[t]，d2[t]···dn[t])为度矩阵，其中di[t] = ∑aij[t].因此系统(2.1)可表示为

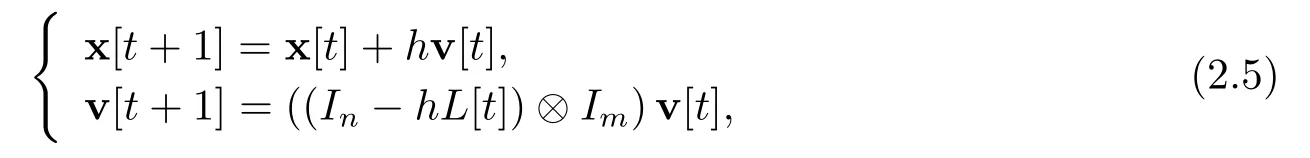
其中x[t]=(x1[t]，x2[t]，··· ，xn[t])，v[t]=(v1[t]，v2[t]，··· ，vn[t]).与文[2]中一样，我们需要假设系统的交互拓扑在切换过程中保持一定连通性.

假设2.2令t0= 0，对于递增的切换时刻序列{ts}s∈N存在正整数T，使得任意s ∈N满足ts+1-ts≤T，并且联合图G([ts，ts+1))存在根结点.

注2.1根据假设2.2，在切换过程中，并不需要图G在每时每刻都具有生成树，仅要求时间间隔不超过T的时间段([ts，ts+1))内的联合图G([ts，ts+1))具有生成树即可.这在一定程度上保证了交互图在切换过程的连通性，使得图G在连续有限时间内的联合图具有生成树.该假设比文[8]要求图G时刻具有生成树要弱.

为了刻画系统发生集群演化行为的条件，先给出如下引理.

引理2.1[15]设k为一正整数，矩阵Ai(1 ≤i ≤k)为非负n×n矩阵，并且满足对角元素大于零，对任意i图G(Ai)有根结点，则乘积A1A2···Ak是不规则矩阵.

引理2.2[10]设v ∈Rmn，A=(aij)n×n是一个随机矩阵，ω =(A ⊗Im)v，则

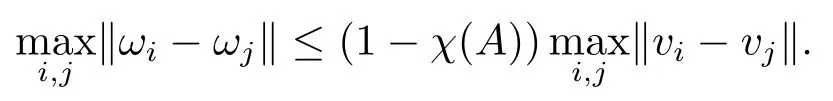
引理2.3[2]假设则对任意t ＞0有

引理2.4(Borel-Cantelli定理) 假设{fk}是一个随机事件列，则有

2)若fk是独立事件且

引理2.5[3]设c1，c2＞0并且p ＞q ＞0，则方程

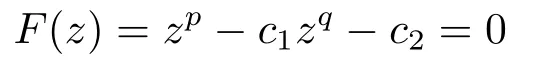
存在唯一正零点z*，并且满足

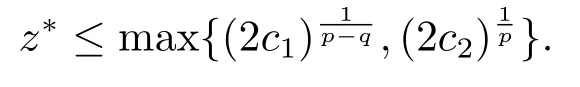
当z ∈[0，z*]时，F(z)≤0.

3.主要结果

在本章中，将研究具有切换和随机故障影响下的C-S模型的群体演化行为.首先建立关于遍历系数期望的不等式，然后借助Borel-Cantelli定理得到关于遍历系数的估计.最后利用代数方程F(z) = zp-c1zq-c2= 0解的性质，证明系统(2.1)的解满足定义2.1，从而证明系统在随机故障影响下发生群体演化行为.根据定义2.1中集群行为的定义，以下推导在依概率1成立情形下进行.

令α=2(n-1)T，根据方程(2.5)以及Kronecker积的性质，可以得到

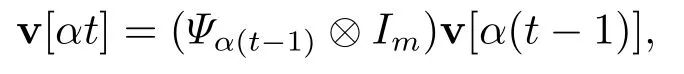
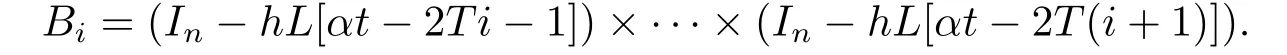
注意到L=D-A，因此上式可写成：

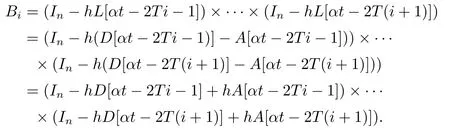
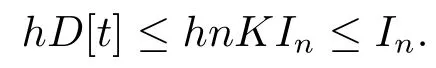
因此

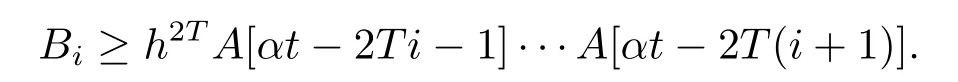
由于随机故障的影响，A[t]的元素均为随机变量，为此先给出随机变量序列的期望不等式.

引理3.1假设为任意递增时间序列，为系统(2.1)-(2.2)的邻接矩阵序列，Ai=(aij[ti])n×n，则有如下期望不等式

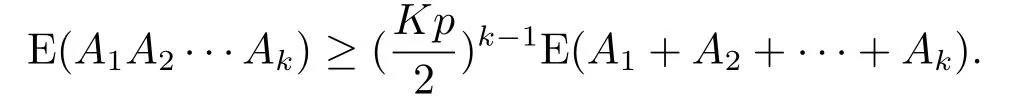
证利用数学归纳法证明.当k =1时，结论自然成立.假设当1 ≤j ≤k-1时，

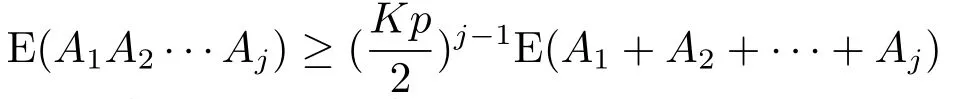
成立.Ai可以写成Ai=+Qi，其中的元素非负，并且有对任意的1 ≤u，v ≤k，鉴于Au与Av是独立的，根据期望的性质可知

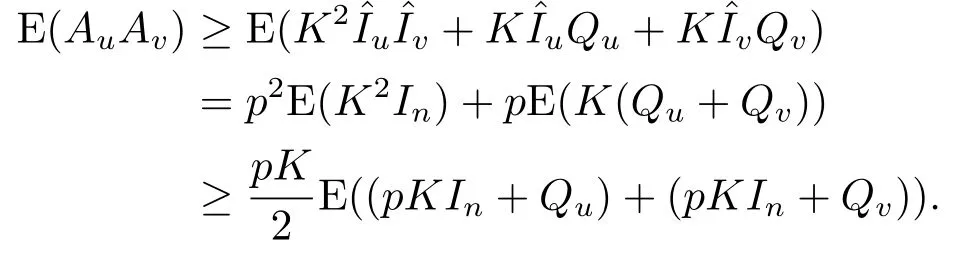
又因为E((pKIn+Qu))=E(Au)，E((pKIn+Qv))=E(Av)，故

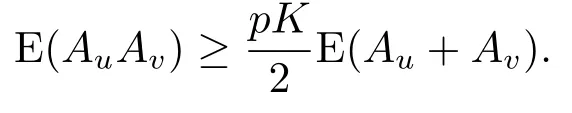
注意到

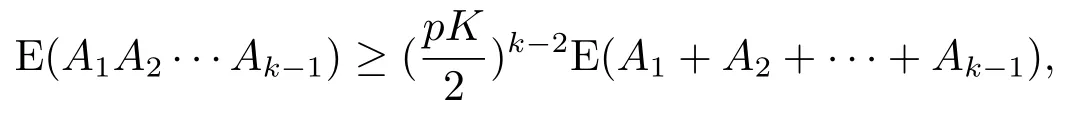
因此

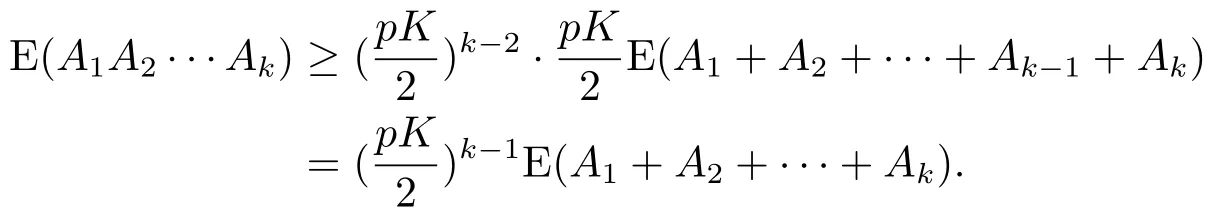
根据引理3.1，可得

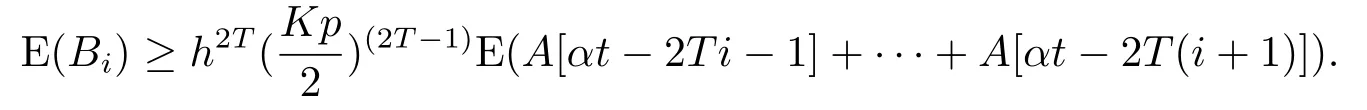
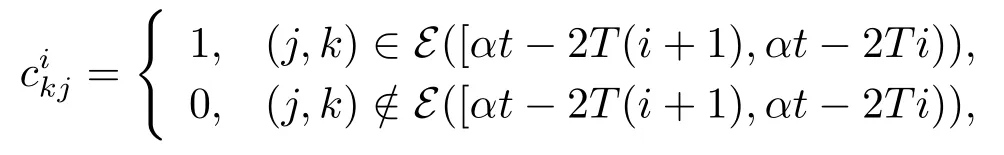
这里E([αt-2T(i+1)，αt-2Ti))为联合图G([αt-2T(i+1)，αt-2Ti))的边集.令

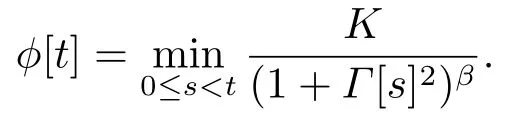
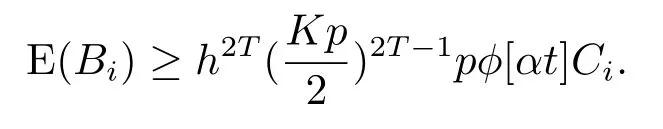
由于Bi相互独立，从而可得

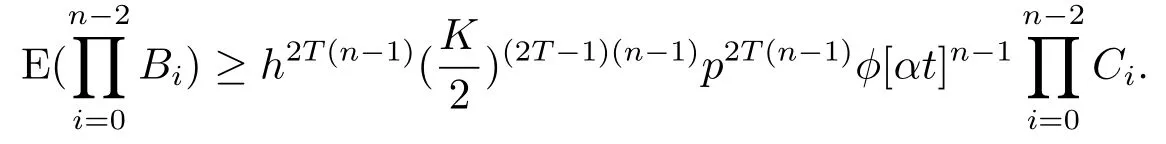
另一方面，根据假设2.2以及区间[αt-2T(i+1)，αt-2Ti)长度大于T，因而存在其子区间[tk′，tk′+1)使得G([tk′，tk′+1))有根节点，从而G([αt-2T(i+1)，αt-2Ti))=G(Ci)有根结点.进而根据引理2.1，可知矩阵∏Ci是不规则矩阵.因此

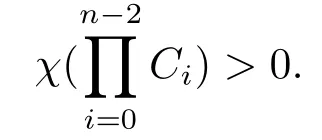
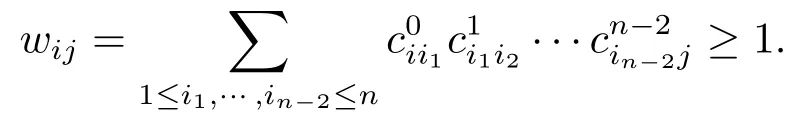
根据遍历系数的定义得

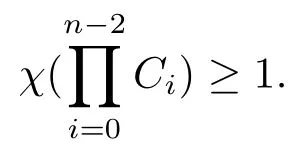
故

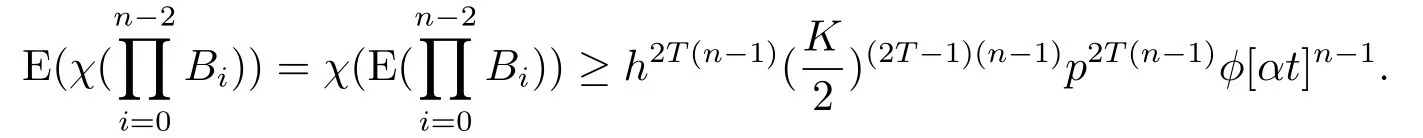
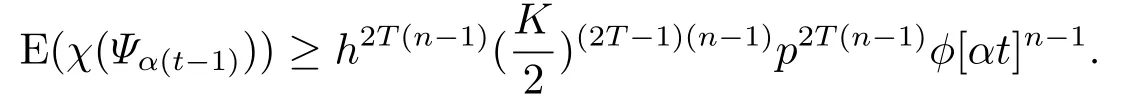
引理3.2对于系统(2.1)-(2.2)，如果假设2.1和假设2.2成立，且存在与t无关的随机变量τ0，使得当t ＞τ0时有

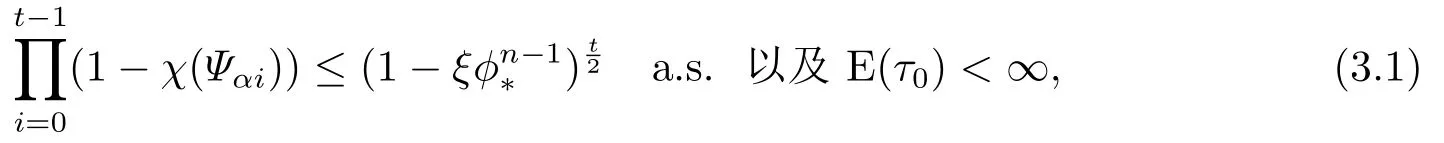
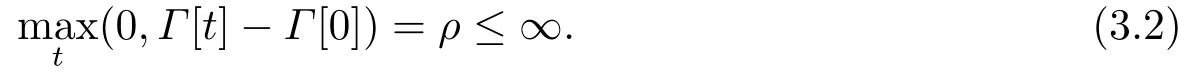
证由于Bi是随机矩阵，可知也为随机矩阵.所以对∀t ＞0，

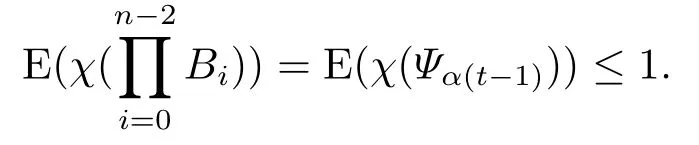
因此

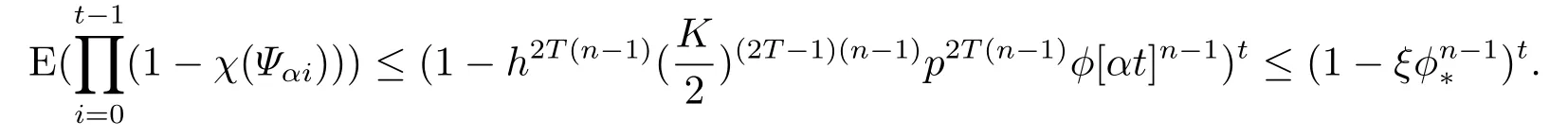
若ρ=∞，则有φ*=0，因此当t ≥1时，(3.1)式显然成立.若ρ ＜∞，则φ*＞0，ξφ*＜1，进而根据Markov不等式可得

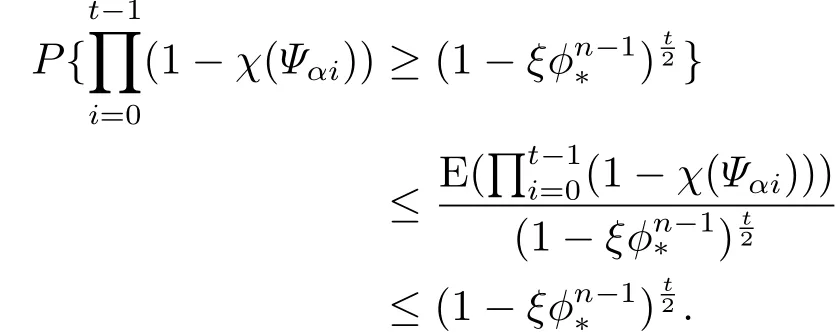
事件At表示集合由上面得根据引理2.4(Borel-Cantelli定理)，我们可得即所以这里为At的补.令显然Bk⊇Bk-1，定义与t无关的随机变量τ0，其满足τ0(ω) = k当且仅当ω ∈Bk-Bk-1.所以对任意t ≥k，有ω ∈Bk因而ω ∈又因为所以当t ＞τ0时依概率1有又因为因此

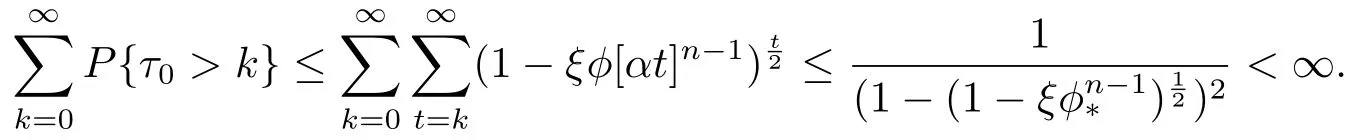
定理3.1具有切换拓扑和随机故障影响的系统(2.1)-(2.2)满足假设2.1和2.2以及并且下面条件之一成立:

证令(3.2)式成立对于ρt=ρ，φ[t]=φ*，因此引理3.2可以写成: 存在随机变量τ0，当t ＞τ0时

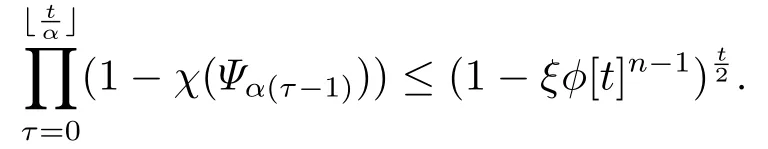
由于v[at]=(Ψα(τ-1)⊗Im)v[α(t-1)]，根据引理2.2有

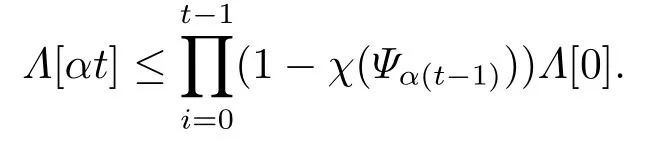
当t足够大时，由式(2.5)可得

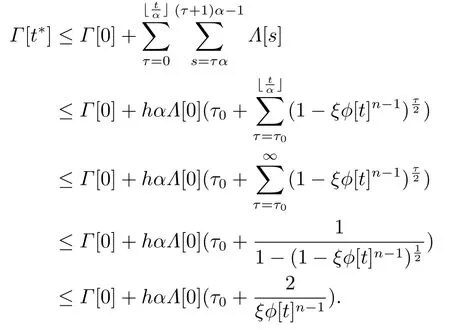
因此

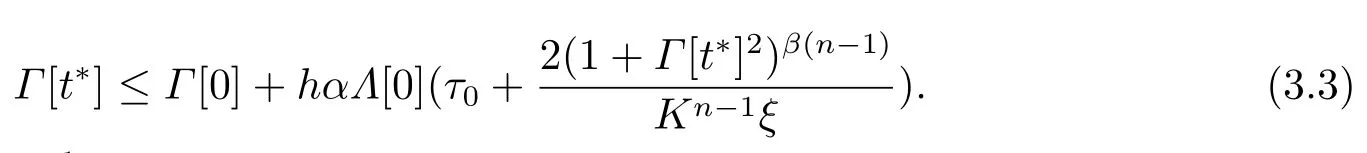
记z[t]=(1+Γ[t*]2)，则上式可改写为

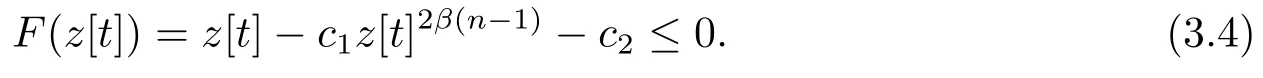
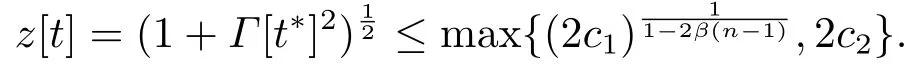
从而对任意t 有

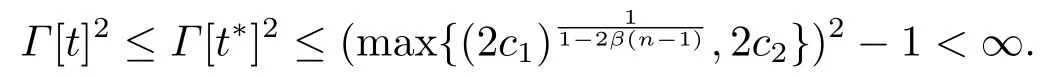
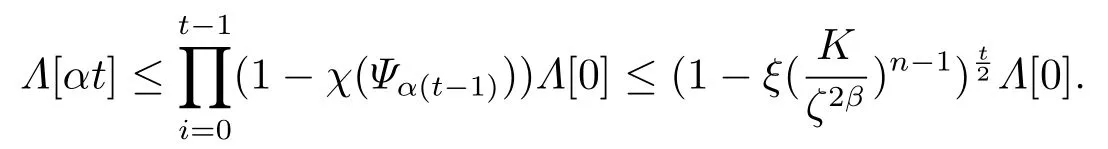
因此，当t ＞ατ0+1时，

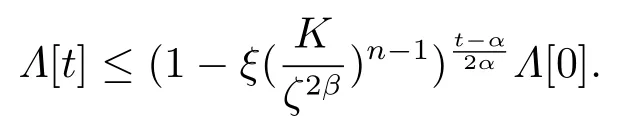
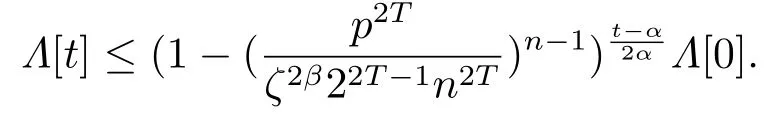
另一方面，对任意时刻t2＞t1＞τ0，ij，

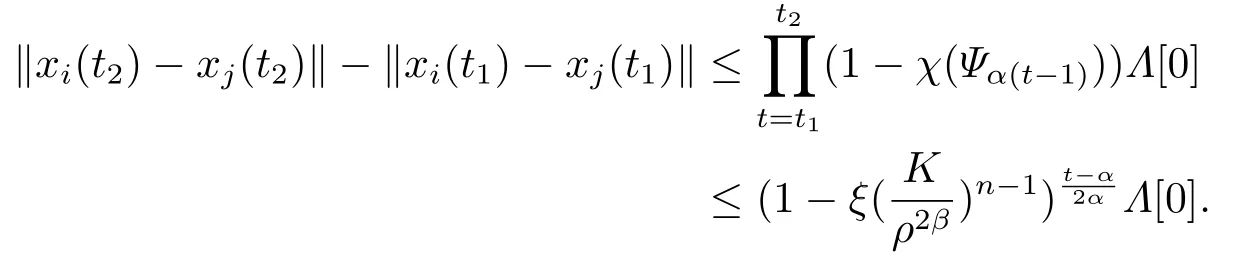
由此可知存在yij＜∞使得limt→+∞‖xi(t)-xj(t)‖→yij.

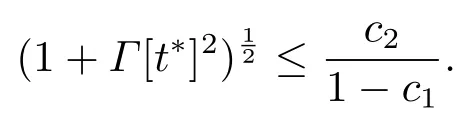
从而对任意t，Γ[t*]有界.类似情形1，易知系统(2.1)-(2.2)发生集群演化行为.

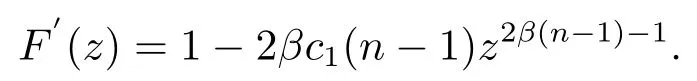
注意到2β(n-1)＞1，故F′(z)有且只有一个零点鉴于

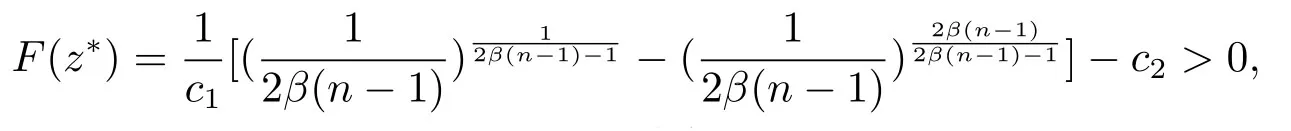
以及F(0) = -c2＜0和limt→+∞F(t) = -∞，我们可知方程F(z) = 0存在两个零点z1和z2使得z1＜z*＜z2以及F(z)＞0对所有z ∈(z1，z2)成立.注意到

从而z[0]＜z*，且F(z[0])＜0.故z[0]＜z1.

下面证明对任意t ＞0，不等式z[t]＜z1成立.

事实上，反设存在t′，使得z[t′]≥z1，且t′为首个满足此条件的点.由于F(z[t′])＜0，这意味着z[t′]＞z2，即因此另一方面，因t′为首个满足此条件的点，故有即从而有

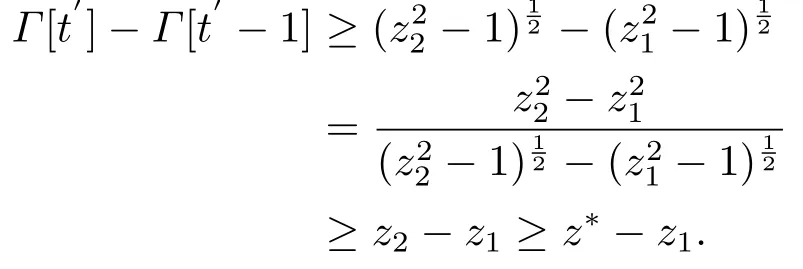
由微分中值定理可知，存在ε ∈(z1，z*)使得

又因为

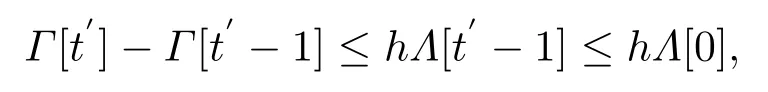
所以F(z*)≤hΛ[0].这与情形3的条件矛盾.因此对任意t有z[t]≤z1≤z*.故

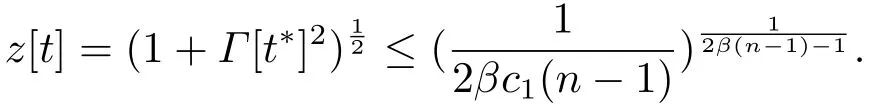
从而对任意t，Γ[t*]有界.类似情形1，易知系统(2.1)-(2.2)发生集群演化行为.定理证毕.

4.数值仿真

本节我们将对带有切换拓扑和随机故障影响的C-S模型进行数值仿真分析，进一步探索切换拓扑以及随机故障对系统的动力学行为的影响.

首先，我们通过数值仿真方法验证定理3.1.为此，假定个体数n = 6，模式集P由3种不同的拓扑模式组成，即P = {G0，G1，G2}，对应拓扑结构见图4.1-4.3所示，其中G0，G1具有根结点(图中有生成树).而G2并没有根结点，因为G2中任意一点都不能到达节点4.构造选择函数显然选择函数满足假设2.2.

数值仿真结果如下:

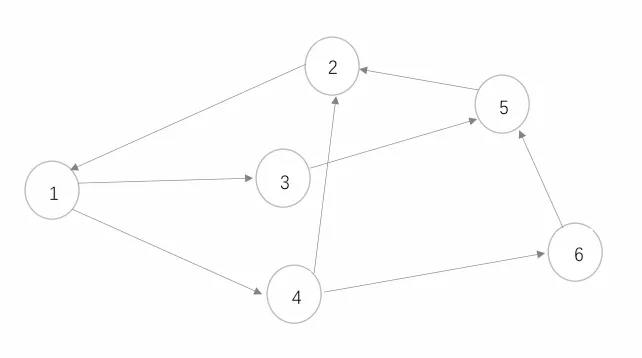
图4.1 G0

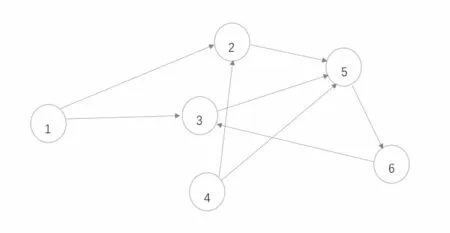
图4.2 G1

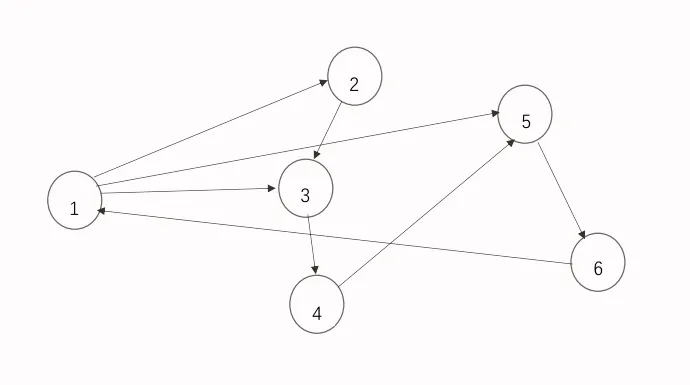
图4.3 G2

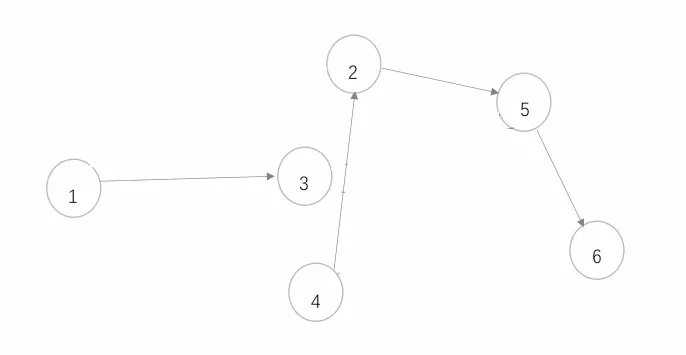
图4.4

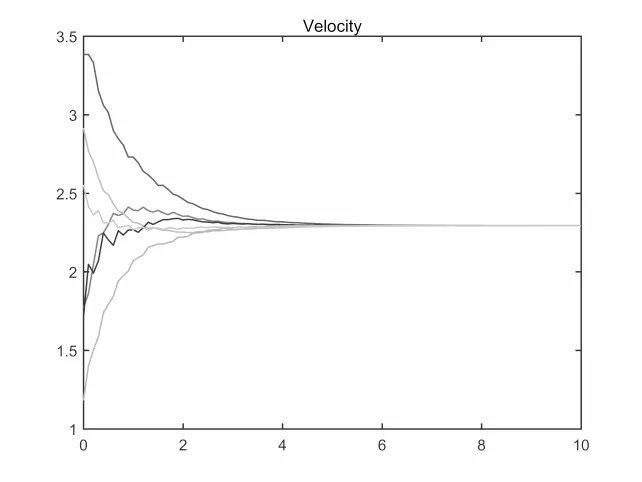
图4.5 β ＜0.1，速度v变化

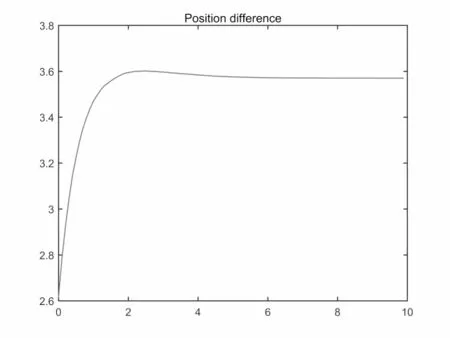
图4.6 β ＜0.1，位移差Γ变化

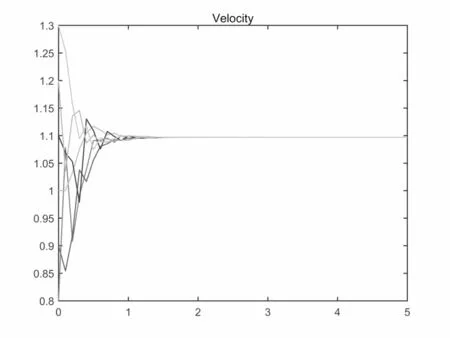
图4.7 β =0.1，速度v变化

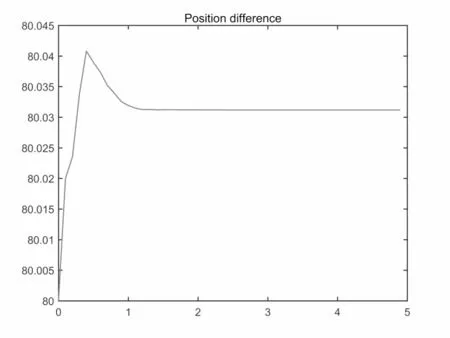
图4.8 β =0.1，位移差Γ变化

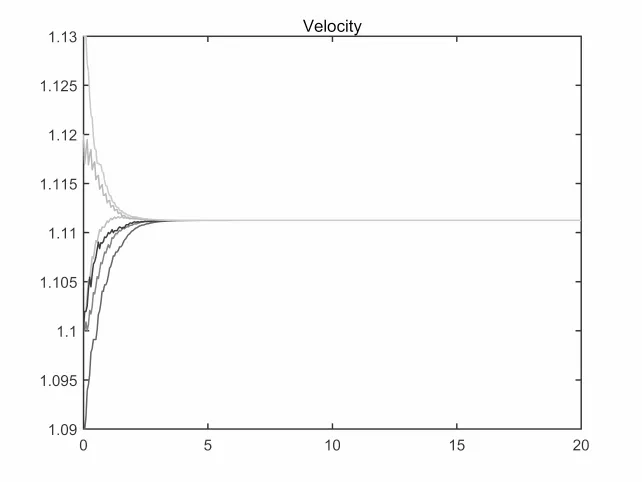
图4.9 β ＞0.1，速度v变化

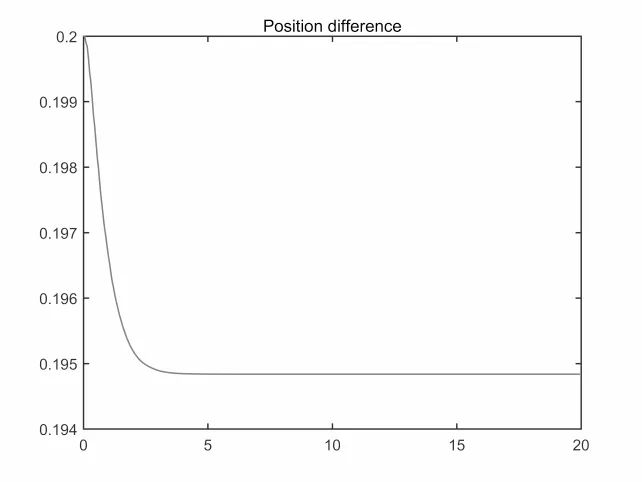
图4.10 β ＞0.1，位移差Γ变化

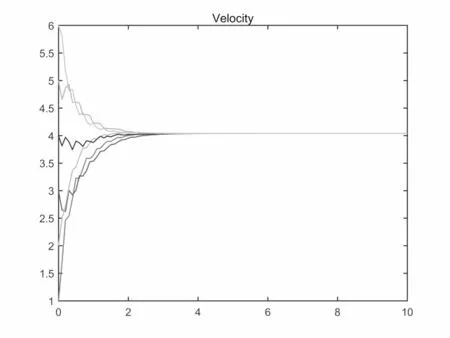
图4.11 故障概率λ=0.05，速度v变化

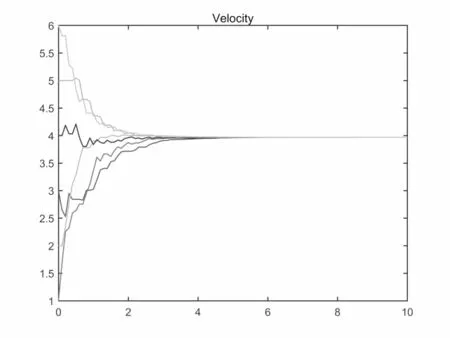
图4.12 故障概率λ=0.3，速度v变化

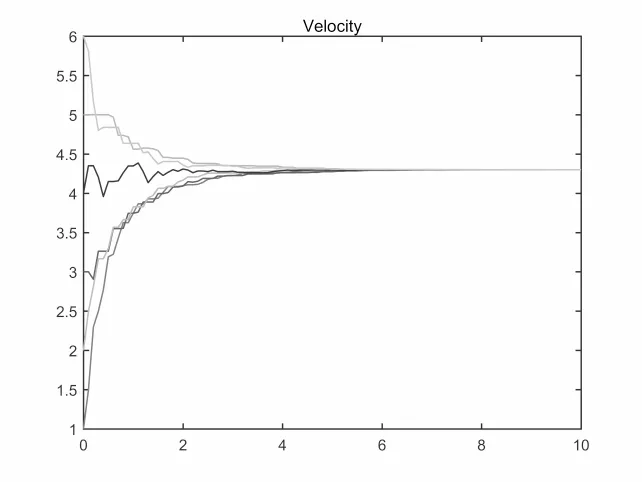
图4.13 故障概率λ=0.5，速度v变化

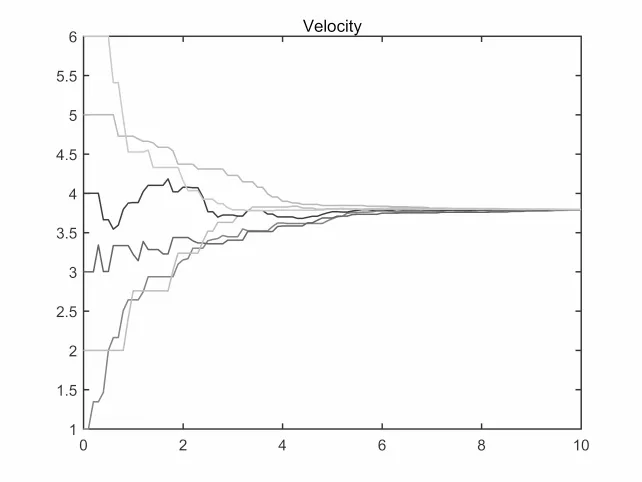
图4.14 故障概率λ=0.7，速度v变化

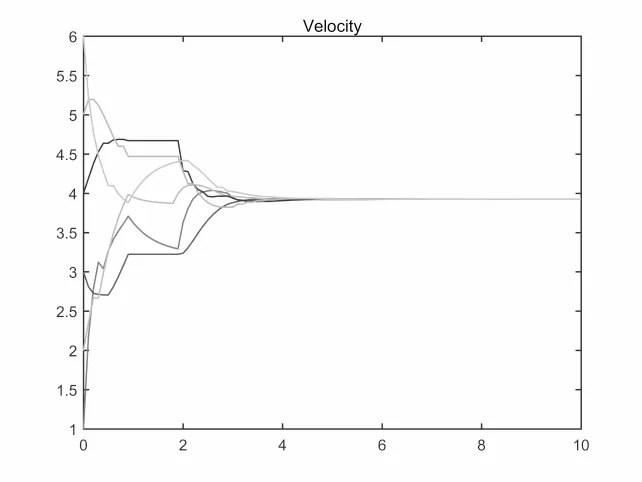
图4.15 最大切换间隔1s，速度v变化

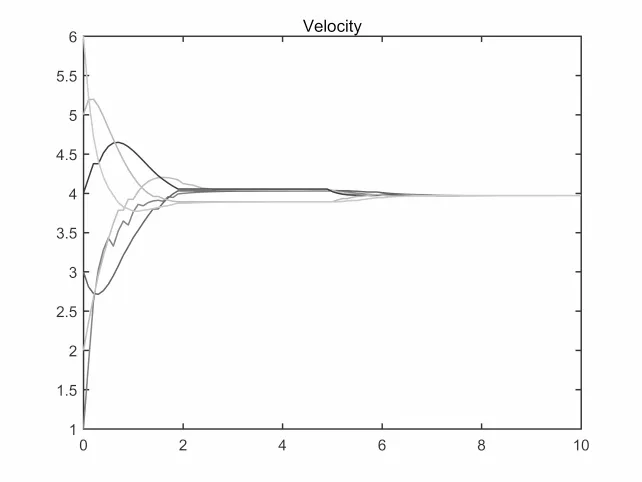
图4.16 最大切换间隔3s，速度v变化

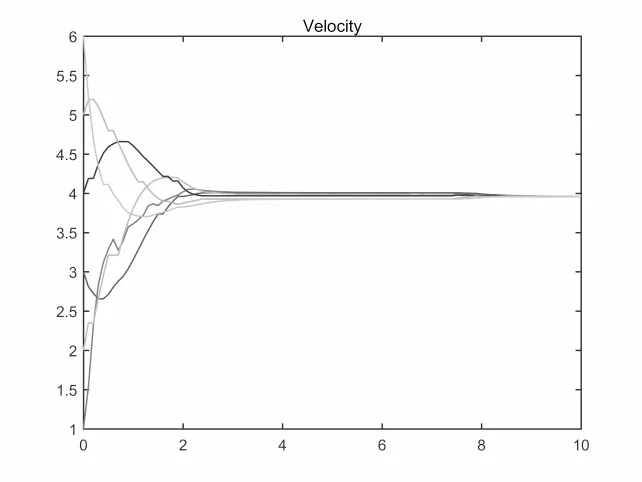
图4.17 最大切换间隔5s，速度v变化

关于故障概率对集群演化行为的影响，数值仿真结果显示: 集群收敛速度与故障概率密切相关，故障概率λ = 1-p越大，收敛速度越慢.取β =T = 1，K = 2，h = 0.1，初始速度和位置为V0= [1，3，2，4，5，6]，X0= [1，3，2，4，5，6].故障概率分别取0.05，0.3，0.5，0.7，对应的收敛时间为3.2s，4.8s，5.8s，9.6s.从图4.11-4.14中可以看出故障概率越大收敛速度越慢.这与定理2.1的结论是一致的.另外切换时间和切换函数σ(t)有关.如果改变切换函数使得切换间隔变长.如果要继续满足假设2.2则T将变大，这将会影响集群演化.将图4.3所示的拓扑结构改变为图4.4中所示的拓扑结构.显然没有生成树，且数值模拟表明在该拓扑下系统2.1不能形成集群.图4.15-4.17分别表示最大切换间隔为1s，3s，5s时系统2.1速度变化.

从图中可以看出，如果模式集P中存在不能形成集群的拓扑模式，随着切换间隔增大，集群收敛速度变慢.当切换间隔趋于无穷时，系统的集群演化行为将会遭到破坏.

5.总结

本文研究了具有切换拓扑和随机故障影响的C-S模型的集群演化行为，证明了当β ＜时，系统几乎必然发生无条件群体行为; 当时，在特定约束条件下，系统也几乎必然发生群体演化行为.特别的，当约束条件与初始速度有关，而与初始位移无关; 当时，约束条件与初始速度和初始位移都有关.进一步研究发现，随机故障也会影响集群演化速度，并且集群收敛速度随着故障概率λ的增大而减慢.