二维趋化N-S方程解的唯一性准则
2021-01-07郭猫驼苑佳
郭猫驼,苑佳
(北京航空航天大学数学科学学院,北京100191)
1.引言
在本文中,我们研究的是不可压趋化Navier-Stokes方程(简称为趋化N-S方程),其表达式如下:
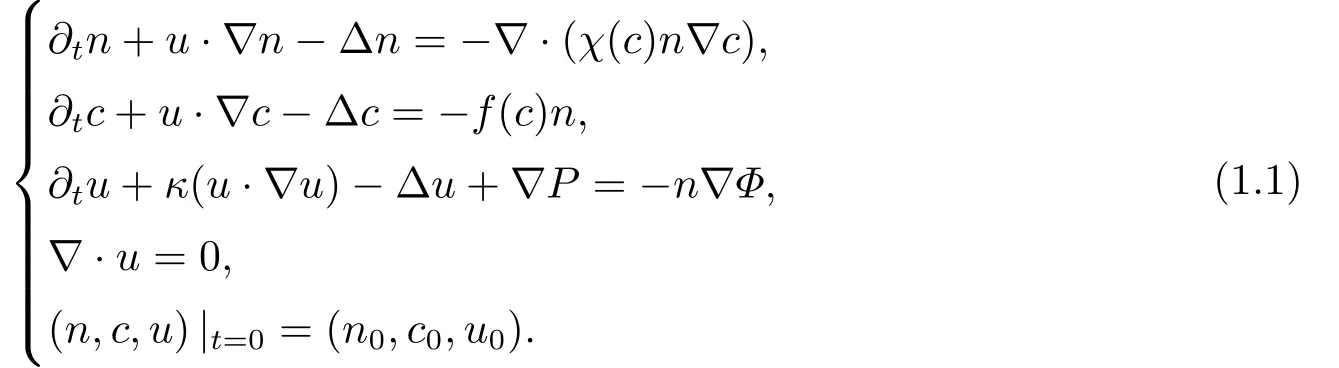
系统(1.1)描述的是不可压流体中微生物的趋化现象,关于这类方程的解的适定性问题有很多的研究工作.在2010年,DUAN和Lorz[3]证明了系统(1.1)在二维以及三维的有界区域(不含通量的边界条件)内弱解的局部存在性;随后,LIU和Lorz[4]在关于χ(c),f(c)的假设
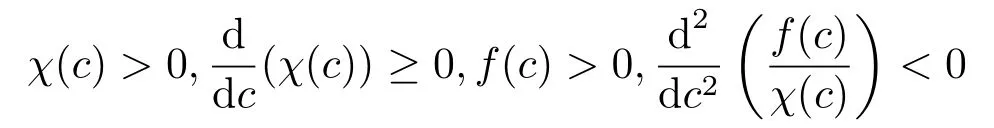
以及c0,Φ的初值很小的条件下,得到了系统(1.1)在二维空间中的整体存在性.在2013年,系统(1.1)的古典解在二维和三维空间中的局部存在性在文[5]中被建立.在2014年,Chae,KANG和Lee[6]证明了在二维以及三维空间中,系统(1.1)光滑解的局部适定性并且在Hm,m ≤3的框架中建立了解的某些爆破准则.之后,ZHANG[7]把该结果拓展到了Besov空间.同样在2014年,在κ = 1且χ(c)为常数的情况下,ZHANG和ZHENG[8]获得了能量解的整体适定性.在2017年,对系统(1.1)考虑一个额外的细菌密度增长源时,Braukhoff[9]在二维空间上建立了古典解的整体存在性和唯一性以及在三维空间下弱解的整体存在性.同时在2018年,在满足‖n0‖L1(R2)足够小并且对于χ(c),f(c)满足χ(c),f(c),χ′(c),f(c) ≥0时,解的整体适定性以及时间衰减估计在文[10]中被建立.但是在三维条件下,系统(1.1) 带有大初值问题的解是否整体存在、是否爆破依然是一个公开的问题.
我们要研究的是二维趋化N-S方程系统中的一类,其表达式如下:
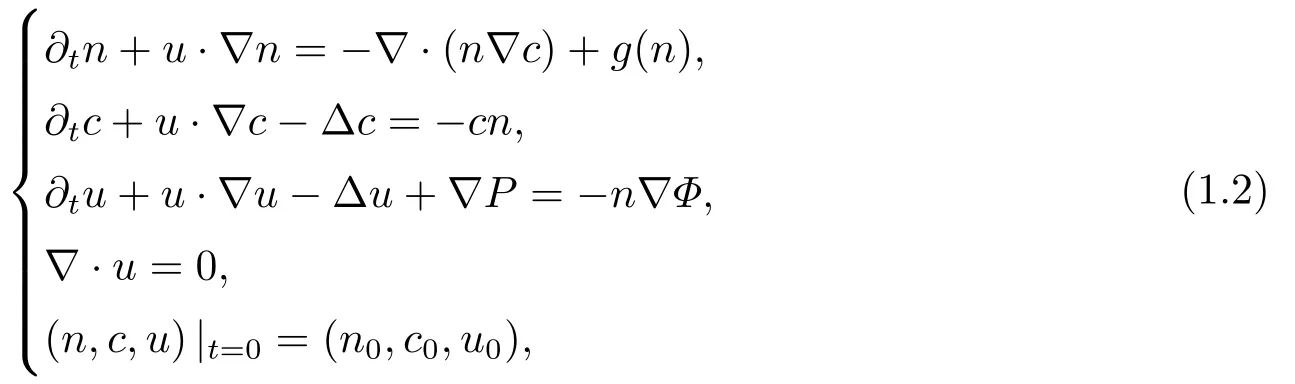
对于上述系统(1.2),在初值属于X0≜{(n0,c0,u0)|n0∈L1∩L2(R2),n0>0;c0∈L2∩L∞(R2),c0>0;u0∈H1(R2)}时,从文[1]中已经有了弱解的存在性的结果,其结果如下:
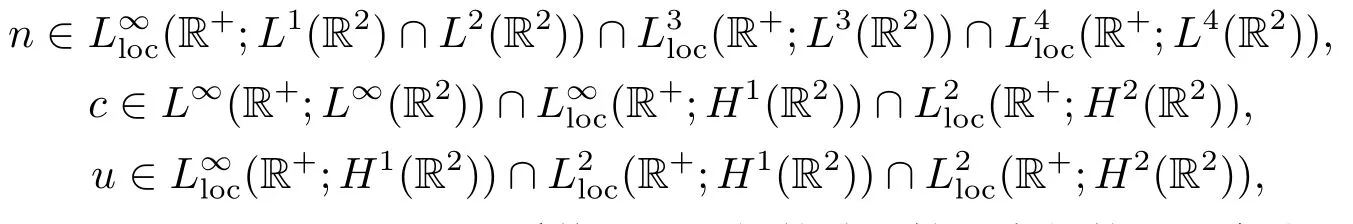
并且满足n(x,t) >0,c(x,t) >0.但是系统(1.2)弱解的唯一性研究依然是一个公开的问题,本文主要工作就是为系统(1.2)的唯一性研究做进一步的推进工作,我们得到了系统(1.2)的唯一性准则,结果如下.
定理1.1对于任意的(n0,c0,u0)∈X0以及∇φ ∈L∞(R2),若系统(1.2)的弱解满足
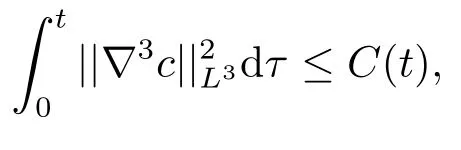
那么系统(1.4)的弱解具有唯一性.
2.预备知识
首先引入如下的单位分解定理[2]:
定理2.1设Ψ是一个以原点为中心,长半径为短半径为的环,则存在两个径向函数满足且
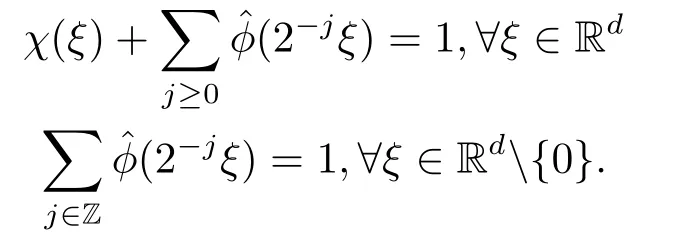
在以上单位分解定理的基础上,引入一些记号如下:
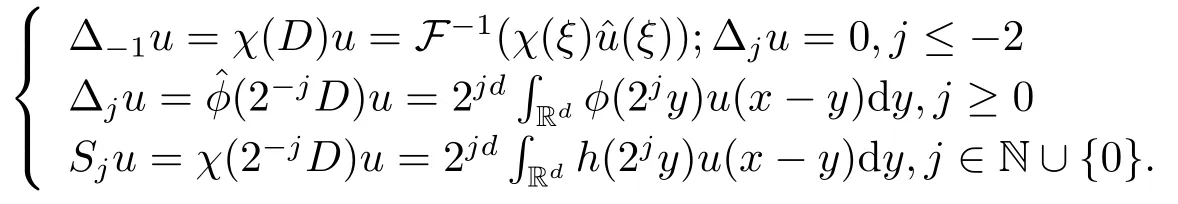
根据以上的Littlewood-Paley算子Δj的定义,有如下的非齐次Littlewood-Paley分解
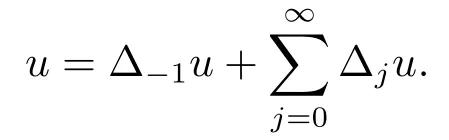
同时可以有如下非齐次Besov空间的定义:
定义2.1设(p,r)∈[1,+∞]2,s ∈R,那么非齐次Besov空间(Rd) 定义为:
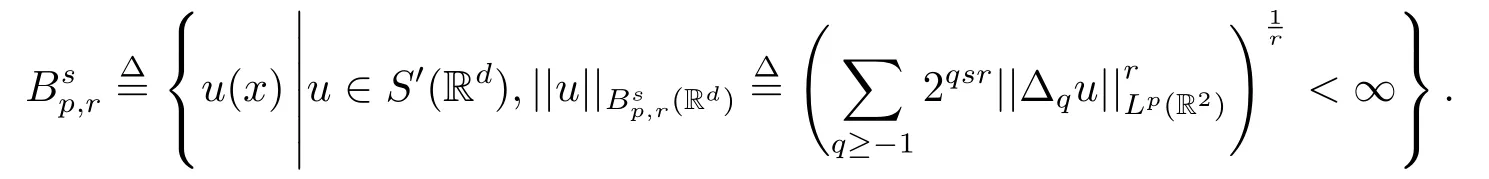
定义2.2当T >0,ρ ≥1时,记表示满足下列表达式的所有缓增广义函数的集合,
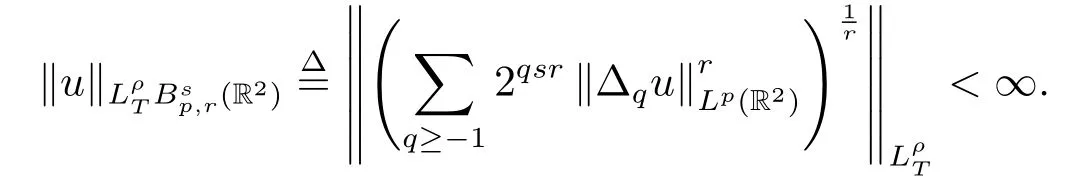
定义2.3当T >0,ρ ≥1时,我们记表示满足如下条件的缓增广义函数u的集合
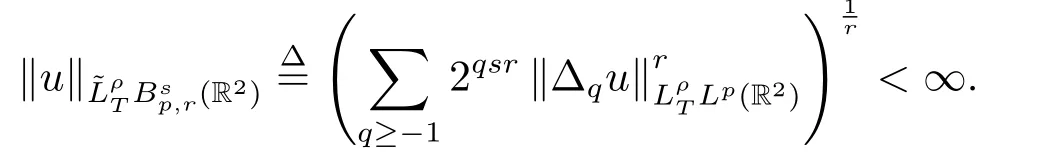
根据Minkowski不等式,发现:当s ∈R,ρ ≥1且(p,r)∈[1,∞]2时,如果r ≥ρ,嵌入到如果ρ ≥r,嵌入到在本文定理证明的过程中需要用到以下引理.
引理2.1(Bernstein不等式) 令1 ≤p ≤q ≤∞,假设f ∈Lp,那么存在一个不依赖于f和j的常数C,满足
3.定理1.1的证明
为证明定理1.1,我们需要首先证明以下的引理3.1与引理3.2,这两个定理对于定理1.1的证明有很重要的作用.
引理3.1在初值属于X0条件下,系统(1.2)的弱解有如下正则性:

证首先用算子Δq(q ≥0)作用系统(1.2)的第三个方程两边,从而有
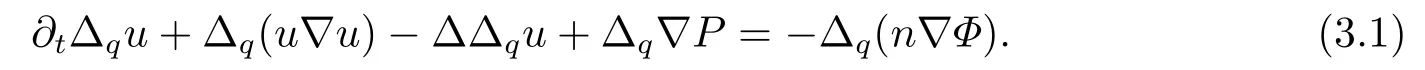
然后在上述式子(3.1)两边同时乘以Δqu,并且对于空间变量积分,应用Bernstein不等式,可以得到
学生在教师阶梯式课外阅读教学方法中,将会根据自身的阅读水平接触到适合自己的读本,有利于自己在能力范围内进行阅读学习,循序渐进地提升自己的阅读能力。教师不应急于求成,而是通过有效的课外阅读教学方法,逐步实现自身的教学目标,也是教师教学质量和水平不断提升的有力展现,可以使学生在教师教学方法的帮助下,自身的阅读能力得到发展和完善。
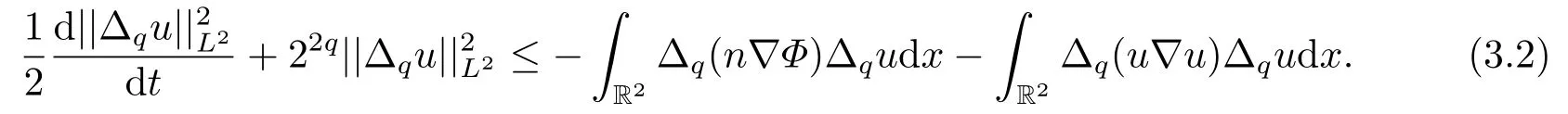
将方程式子(3.2)的两边同时乘以tα22q,0 <α <1,方程变为
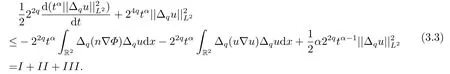

把I,II的估计式(3.4),(3.5)式代入到(3.3)式,并且两边同时对于时间t进行积分,从而有
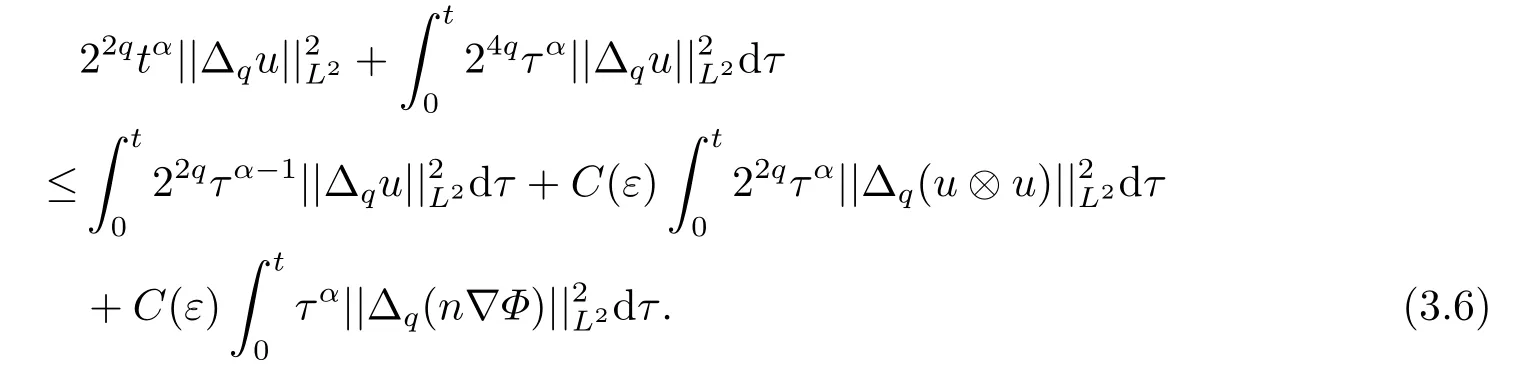
对式(3.6)两边同时对q ≥0进行求和,可以把(3.6)式转化为如下(3.7)式
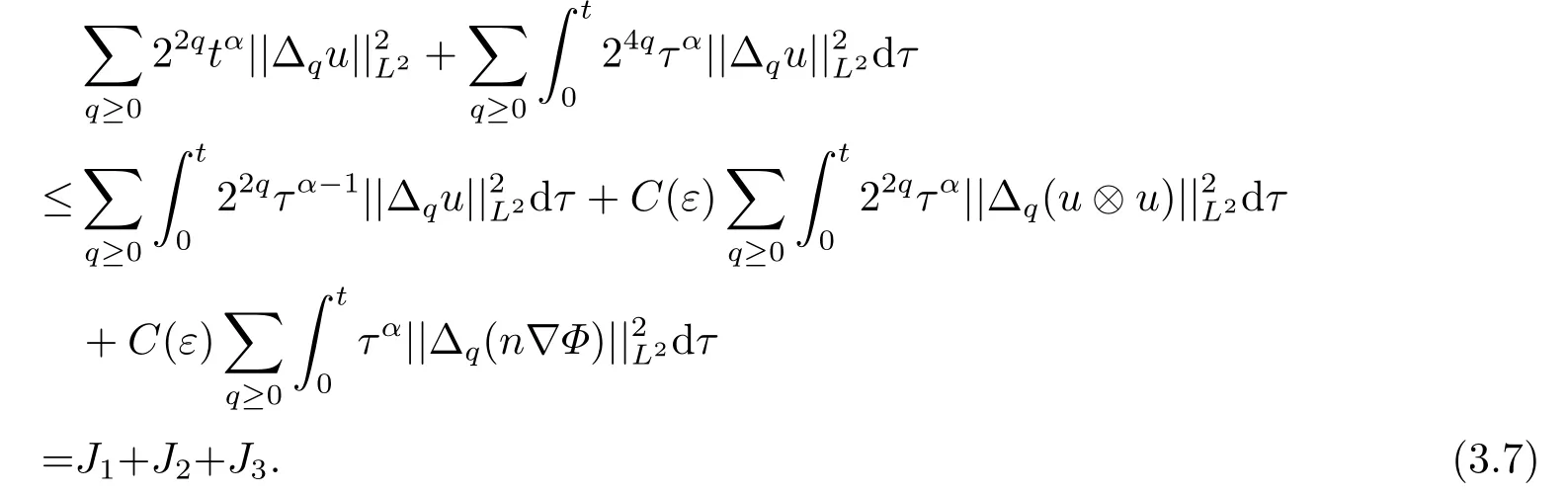
对于上述(3.7)式右边的J1,J2,J3项,利用Besov空间与Sobolev空间的嵌入关系,以及Hlder不等式,有如下估计
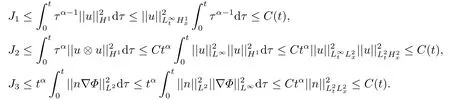
把上述J1,J2,J3所得到的估计结果累加到(3.7)式中,有如下(3.8)式:
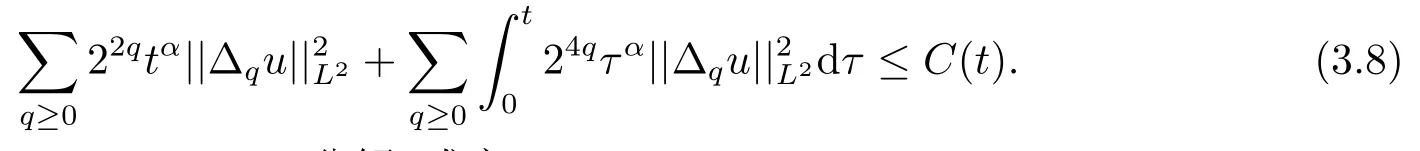
通过使用非齐次的Littlewood-Paley分解,成立
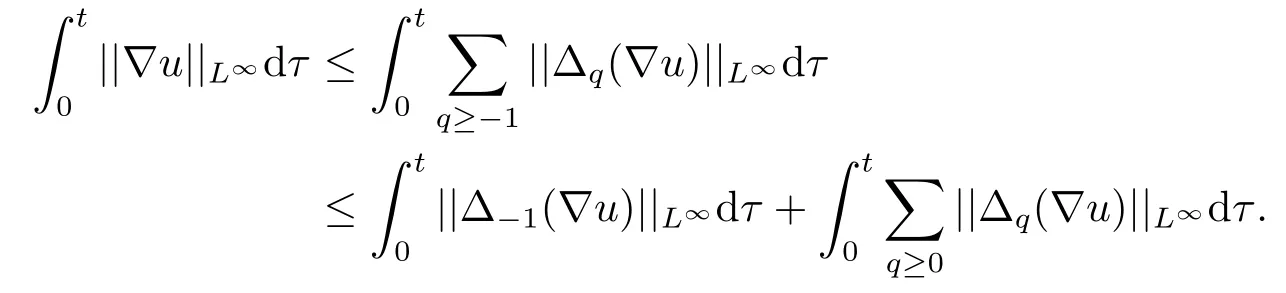
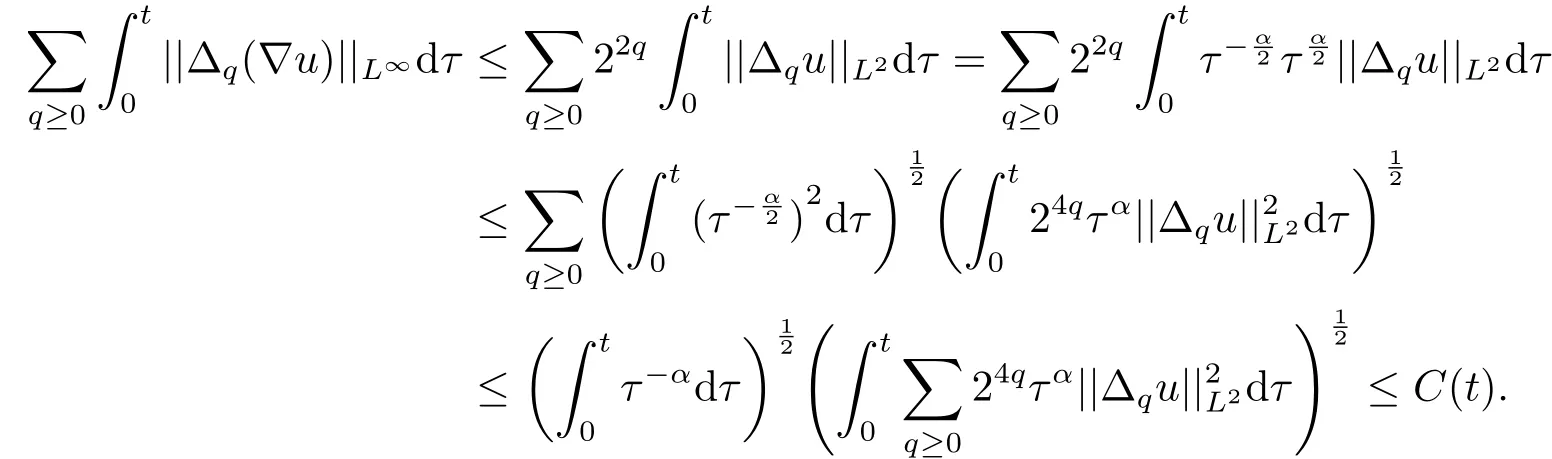
由于
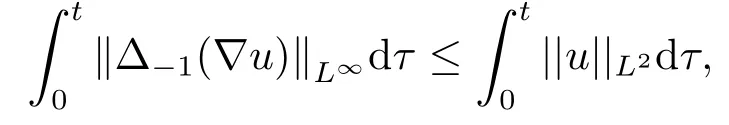
所以可以得到

利用同样的方法,也可以得到
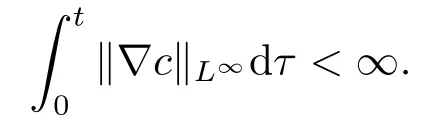
引理3.2若系统(1.2)的弱解(n,c,u)满足那么有

证首先对系统(1.2)的第一个方程两边用∂i作用,并把g(n)=n(1-n)(n-a)代入,就有
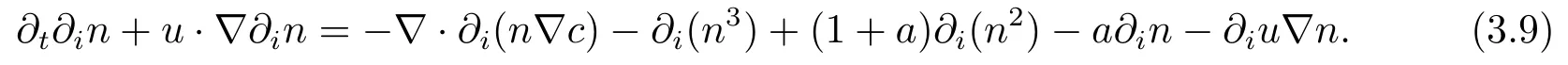
对于上述(3.9)式做L3-估计得
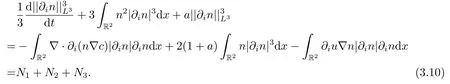
对于N1,N2,N3,分别利用Hlder不等式和Young不等式,有
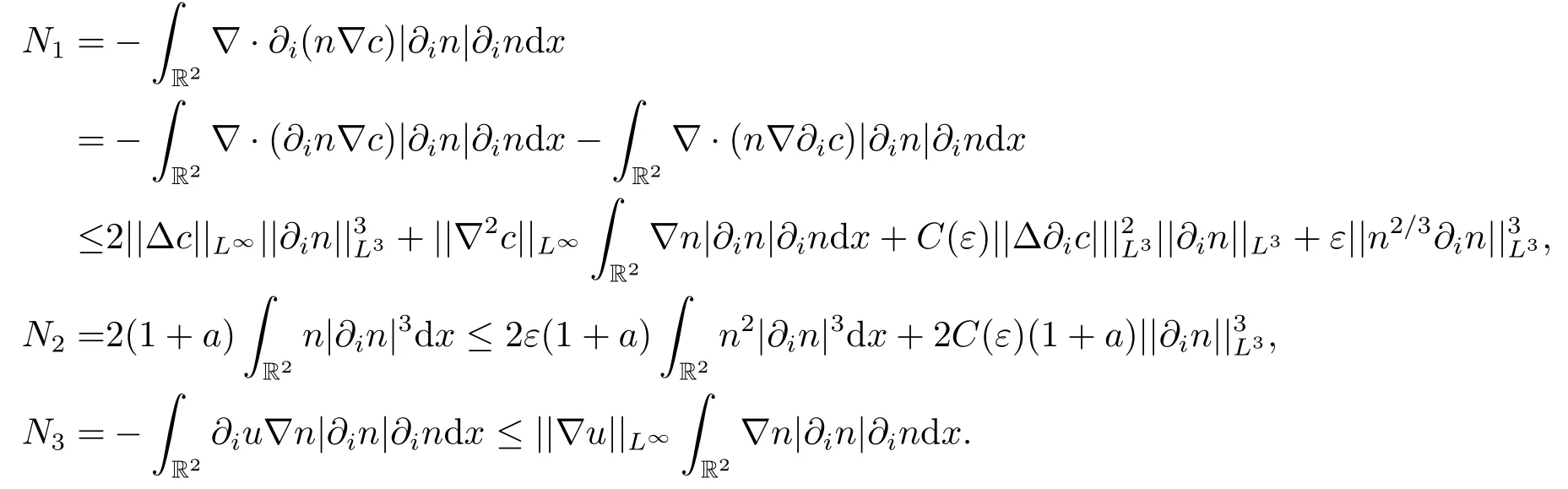
把N1,N2,N3估计带入到(3.10)式,并且两边同时对于i求和,能够得到
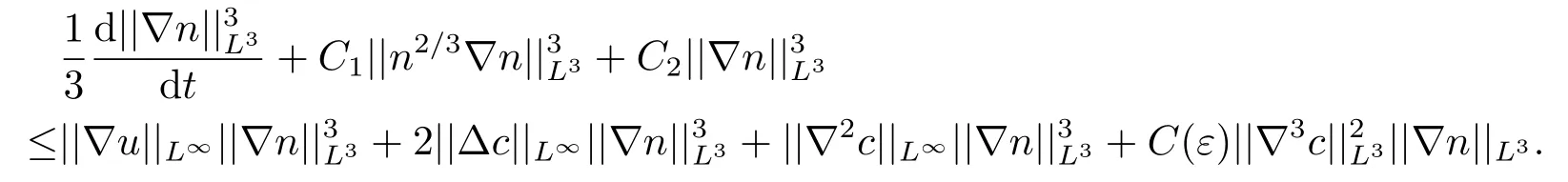
对于上式两边同时除以||∇n||L3,可以得到
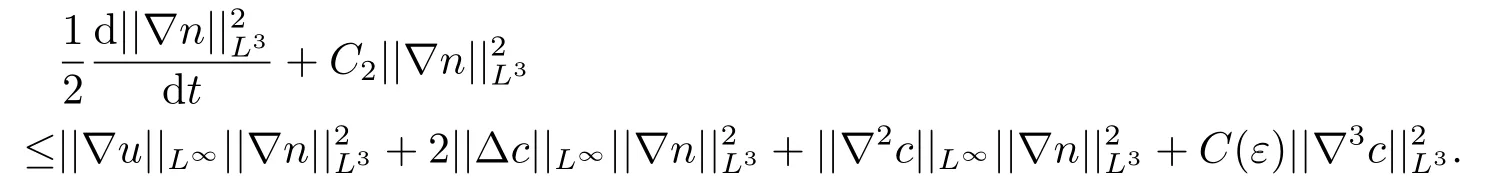
联系已经证明的引理3.1的结果和引理3.2已给的条件,由Gronwall不等式可得
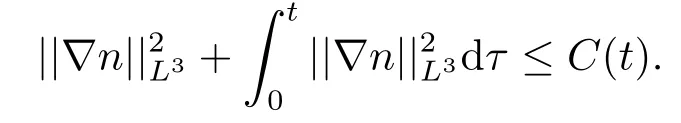
定理1.1的证明假设系统(1.2)有两个弱解(n1,c1,u1)和(n2,c2,u2),利用做差法,令δn =n1-n2,δc=c1-c2,δu=u1-u2,由此我们可以建立系统(1.2)的差分方程组
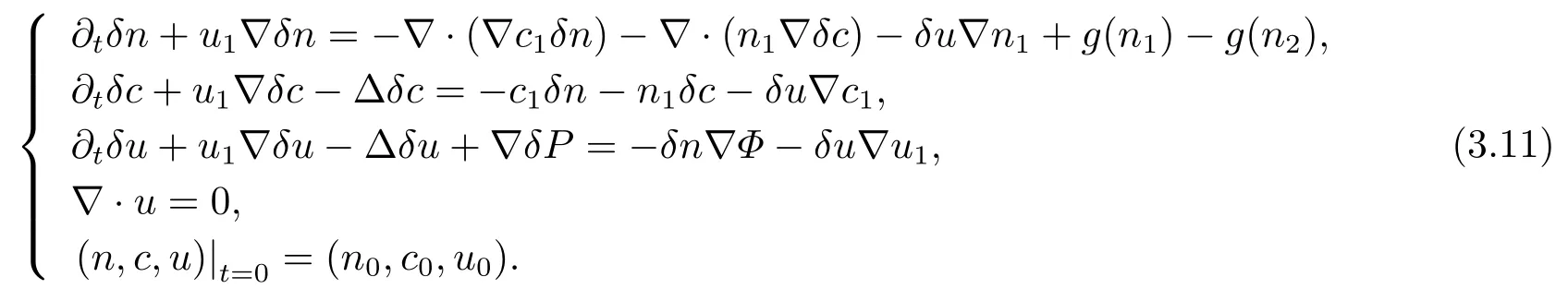
分别对于上述系统(3.11)的第一个,第二方和第三个方程做L2-估计,可以得
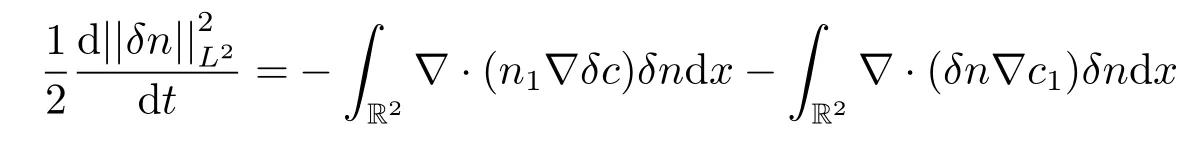
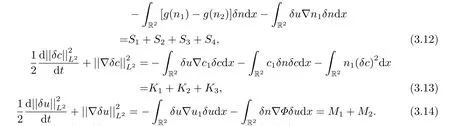
对于S1,S2,S3,S4应用利用Hlder不等式以及Young不等式,就有
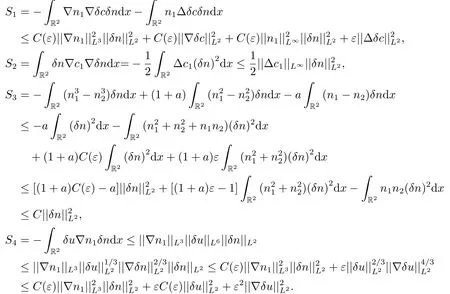
同理对于K1,K2,K3,M1,M2利用Hlder不等式以及Young不等式,可以得到
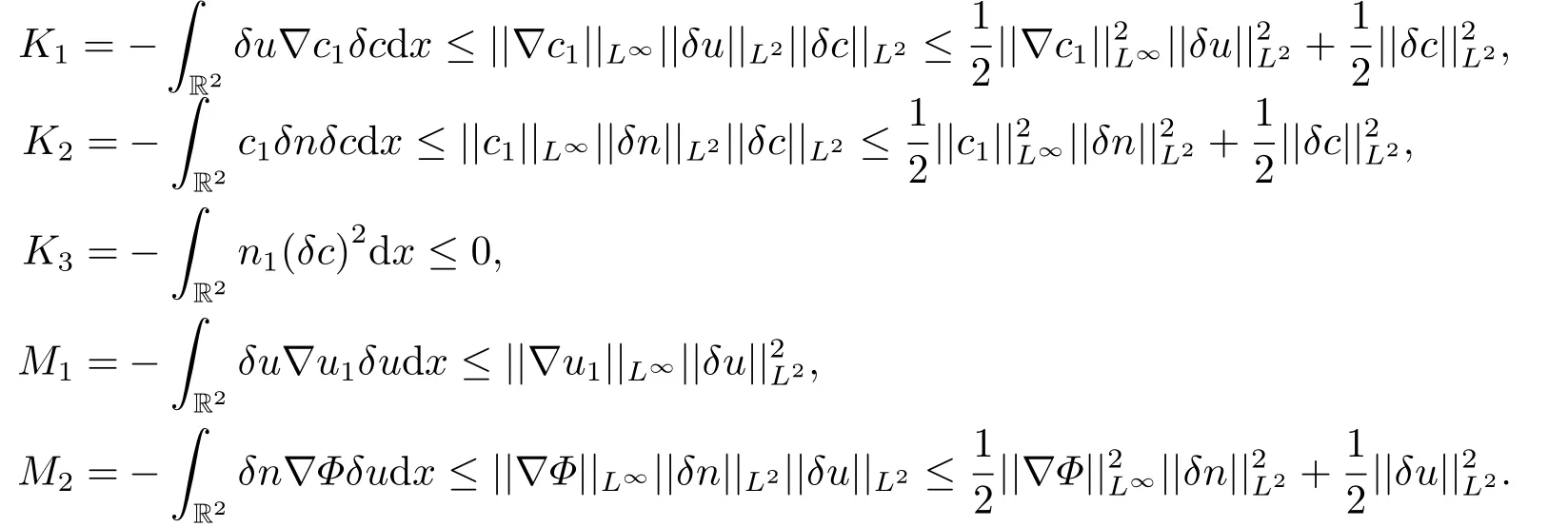
把上述得到的S1,S2,S3,S4,K1,K2,K3,M1,M2估计导入到(3.12),(3.13),(3,14)式,并且把得到的三个式子累加,就有
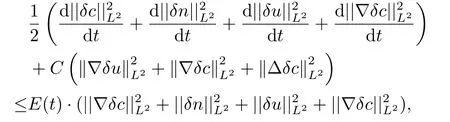
其中
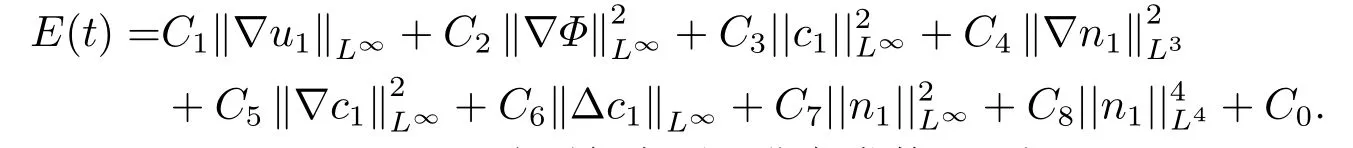
而C,C0,C1,C2,C3,C4,C5,C6,C7,C8分别代表不同非负常数.又由于

所以联系所证明的引理3.1与引理3.2,能够推出E(t)是非负可积的.所以利用Gronwall不等式,就有所以n1= n2,c1= c2,u1= u2,在任意的时间[0,T]内成立,由此我们完成了定理1.1的证明.
猜你喜欢
杂志排行
应用数学的其它文章
- New Iteration Method for a Quadratic Matrix Equation Associated with an M-Matrix
- 具有随机保费和交易费用的最优投资-再保险策略
- 带有N策略的不可靠重试队列的均衡策略分析
- A Smoothing Newton Algorithm for Tensor Complementarity Problem Based on the Modulus-Based Reformulation
- The Center Problems and Time-Reversibility with Respect to a Linear Involution
- Boundary Value and Initial Value Problems with Impulsive Terms for Nonlinear Conformable Fractional Differential Equations
