Existence of the Solution for Stochastic Generalized Coupled Differential Riccati Equation

MA Heping(马和平)，HU Chaozhu(胡超竹)

(School of Science，Hubei University of Technology，Wuhan 430068，China)

Abstract: By means of the singular value decomposition，the existence of solution are obtained for the stochastic generalized coupled differential Riccati equation.As an application，we apply the existence results to consider the optimal control of Markovian jump linear stochastic singular system，and obtain the desired explicit representation of the optimal controllers for the optimal control problem with the finite horizon.

Key words: Existence; Stochastic generalized coupled differential Riccati equation;Optimal control; Stochastic singular system

1.Introduction

In many control problem，both in deterministic and in stochastic framework，a crucial role is played by a class of nonlinear matrix differential equations.One of the most intensely studied nonlinear matrix equations arising in mathematics and engineering is the Riccati equation.This equation，in one form or another，has an important role in optimal control problems，multi-variable and large scale systems，scattering theory，estimation，detection，transportation，and radiative transfer.[16]It is known that the boundedness of the solution of the matrix Riccati differential equation (MRDE) with a terminal boundary condition is equivalent to the no-conjugate point to the final time.The solution of this equation is difficult to obtain from two points of view.One is that it is nonlinear，and the other is that it is in matrix form.Readers may refer to [3，5，6，8，10，11，15] for more details.

In realities，the uncertainties are unavoidable.So over the past decades stochastic modeling has played an important role in many branches of science and engineering.The study of systems with stochastic disturbance has gained growing interest over the past few decades，and many research topics on stochastic systems have been investigated(for example，[1，13，17，18] and references therein).For the nonsingular stochastic system without Markovian jump parameter，SUN，LI and YONG[12]have studied the open-loop and closed-loop solvabilities for a general class of stochastic linear quadratic(LQ)problems with deterministic coefficients.Their results bring new insights into the internal structure of the LQ problem and explain the fundamental reason why the weighting matrices in the cost functional could be indefinite.Rami，CHEN and Moore[16]give a equation called generalized differential Riccati equation(GDRE)，via general necessary and sufficient conditions for the solvability of GDRE.Rami，Moore and ZHOU[17]solve an outstanding open problem，which identifies an appropriate Riccati-type equation，also called generalized differential Riccati equation，whose solvability is equivalent to the solvability of the indefinite stochastic LQ problem.By introducing a notion of subsolution for the SRE，DU[4]derives several novel sufficient conditions for the existence and uniqueness of the solution to the SRE.On the other hand，LI and ZHOU[7]successfully extend the state space system to the system with Markov parameter.A system of coupled generalized differential Riccati equations (CGDREs) is introduced to cope with the indefinite stochastic LQ control problem with Markov parameter.Specifically，they proved that the solvability condition of the CGDREs is sufficient for the well-posedness of the stochastic LQ problem.

The singular system contains the state-space form as a special case and thus can represent a much wider class of systems than its state-space counterpart.Singular system is an important class of systems in terms of theoretical and practical significance，and it has received great attention during the past few decades.WANG and LIU[14]consider the linear quadratic optimal control of stochastic singular systems without Markovian jump parameter.They established the existence and uniqueness of the impulse-free solution of nonregular stochastic singular system，and then gave the sufficient conditions for the optimal control problem.ZHANG and XING[19]studied the problems of stability and optimal control for a class of stochastic singular systems.They obtained some new results about mean-square admissibility and investigated finite-time horizon and infinite-time horizon LQ control problems for the stochastic singular system.ZHANG，LIN and XUE[20]concerned with the finite horizon linear quadratic Pareto optimal control problem of stochastic singular systems.By means of the square completion technique，they established a new kind of generalized differential Riccati equations(GDREs)and presented the existence condition of the solution of the GDREs.

For the stochastic singular system with Markov parameter，a problem is how to guarantee existence of the impulse-free solution to the stochastic singular systems with Markovian jumps，and how to establish the existence of a finite set of stochastic generalized coupled differential Riccati equations (SGCDREs).If those problems are solved，naturally，we will ask that can we study well-posed of a finite set of generalized coupled differential Riccati equations? Being directly inspired by those reasons，the purpose of this work is to study the existence of the stochastic generalized coupled differential Riccati equation and application to LQ optimal control for Markov jump linear stochastic singular systems.

The paper is organized as follows.In Section 2，we summarize some basic assumptions，definitions and some useful Lemmas.In Section 3，we establish the existence of the solution for stochastic generalized coupled differential Riccati equation (SGCDRE).In Section 4，as an application，we apply the existence results to consider the optimal control of Markovian jump linear stochastic singular system，and obtain the desired explicit representation of the optimal controllers for the optimal control problem with the finite horizon.

NotationRndenotes the n-dimensional Euclidean space ，Rm×nis the set of all m×n real matrices and R+:=(0，∞).For symmetric matrices P，the notation P ≻0(respectively，P≽0) means that matrix P is positive definite(respectively，positive semi-definite).I is an identity matrix of appropriate dimensions.The superscripts ATand A-1stand for the transpose and the inverse of a matrix A，‖x‖ is the Euclidean norm of the vector x.

2.Preliminaries

In this section，consider the following linear stochastic singular systems with Markovian jumps，modeled by

where x(t) ∈Rnis the system state vector，u(t) ∈Rmis the control input，and ω(t) is a one-dimensional standard Brownian motion that is defined on the given complete probability space (Ω，F，(Ft)0≤t≤T，P).Define the set of all admissible controls Uad=(0，T;Rm).The coefficient matrices A(t，rt)，C(t，rt)∈L∞(0，T;Rn×n)and B(t，rt)，D(t，rt)∈L∞(0，T;Rn×m)，and E ∈Rn×nis a singular constant matrix and we assume that rank(E) = r ＜n.x0∈Rnis the compatible initial condition which is deterministic.This form process r(t) is a continuous-time discrete-state Markov process taking values in a finite set S = {1，2，...，N}with transition probability matrix P :={pij} given by

where Δ ＞0.Here λij≥0 is the form transition rate from i to j (ij)，and

Let the initial values x0and r0be independent random variables; x0is also independent of the σ-algebra generated by {r(t)，t ∈(0，T]}.When the system operates in the ith mode(r(t) = i)，for simplicity，let

Subject to (2.1)-(2.3)，we consider the minimization of

where Ξ denotes expectation，L(r(T))∈L∞(0，T;Rn×n)，Qi(t)∈L∞(0，T;Rn×n)，and Ri(t)∈L∞(0，T;Rm×m)，i ∈S，are symmetric matrices，and Li(t)∈L∞(0，T;Rn×m).For simplicity，we denotes Θ as follows，

in order to meet the demands of subsequent proof，we assume L(r(T)) ≽0 and Θ ≽0.For the existence of the impulse-free solution to the stochastic singular systems with Markovian jumps (2.1)，we impose the following assumptions:

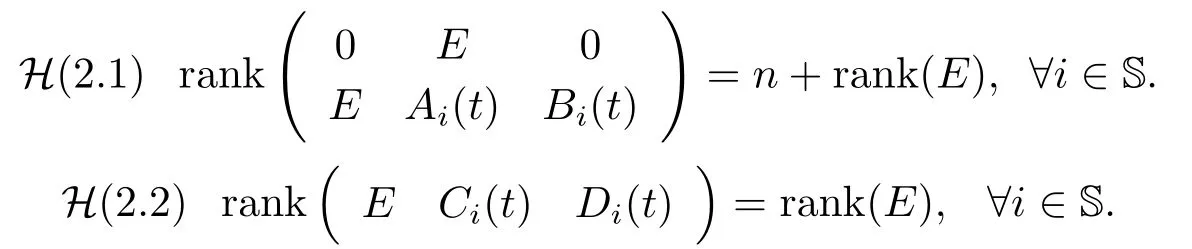
Definition 2.2[9]Let a matrix K ∈Rm×nbe given.Then the matrix K†is called the Moore-Penrose pseudoinverse of K if there exists a unique matrix K†∈Rn×msuch that

Lemma 2.1[18](Variation of constants formula) For any ζ ∈(Ω;Rn)，the equation

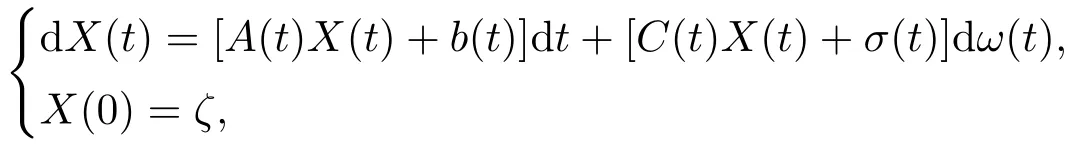
admits a unique solution X(·)，which is represented by the following:

where Φ(·) is the unique solution of the following matrix-valued stochastic differential equation:

where A(·)，C(·)∈L∞(0，T;Rn×n)，b(·)，σ(·)∈L2(0，T;Rn).

Theorem 2.1If the assumptions H(2.1) and H(2.2) hold，then the system (2.1) has a solution on [0，T]，∀i ∈S，in which there is no impulse.

ProofDue to the constant-rank condition of matrix E，we can consider the singular value decomposition.Under the assumption H(2.2)，there exist two orthogonal matrices Mi∈Rn×n，Ni∈Rn×n，∀i ∈S such that

where Σris a nonsingular diagonal constant matrix and Ci1(t) ∈Rr×r，Ci2(t) ∈Rr×(n-r)，Di1(t)∈Rr×m.Accordingly，define

where Ai1(t) ∈Rr×r，Ai2(t) ∈Rr×(n-r)，Ai3(t) ∈R(n-r)×r，Ai4(t) ∈R(n-r)×(n-r)，Bi1(t) ∈Rr×m，Bi2(t)∈R(n-r)×mand let

where ζ1(t) ∈Rr，ζ2(t) ∈Rn-r.By above transformations，the system (2.1) can be transformed into

On the other hand，under the assumption H(2.1)，the rank relation

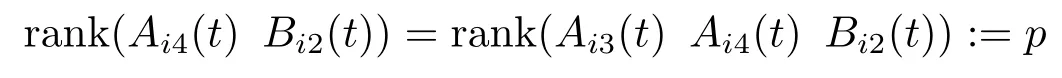
holds.In general，the matrix rank(Ai4(t) Bi2(t)) does not have the full row rank，so there exists a nonsingular matrix Ui(t)，∀i ∈S，such that

Obviously，the system (2.12) is equivalent to the system (2.11).Sincehas full-row rank，then there exists a nonsingular matrix Vi(t)，∀i ∈S such that

Without loss of generality，we assume thathas full-row rank.Otherwise，we can exchange some columns offor some columns ofand then make the same exchanges betweenandLet=uT(t))，wherethen the system (2.12) is equivalently transformed into

The first equation of (2.13) is an ordinary stochastic differential equation，in which ζ1(t)is the state vector andis the control vector.According to Lemma 2.1，the first equation of (2.13) has a solution ζ1(t) on [0，T] under the initial condition ζ1(0) = (0)Mx0.Accordingly，=-exists.Thus，the system (2.13) has a impulse-free solution on [0，T]，which implies that the system (2.1) has a impulse-free solution on [0，T].This completes the proof.

Remark 2.2When Di(t)≡0，S={1}，the result is the same as that of [20].

Remark 2.3When the diffusion term has finite state variables and control inputs，the discussion is similar.

3.Existence of the Solution for SGCDRE

In this section，we establish the existence of the solution for a set of stochastic generalized coupled differential Riccati equations.And we impose the following assumptions:

H(3.1) Ai3(t)≡0 and the matrix Bi(t)，∃t ∈[0，T] is full of column rank.

H(3.2) τi+τj0，where τiand τjare arbitrary eigenvalues of Ai4(t)，∀t ∈[0，T].

Theorem 3.1Assume that H(3.1) and H(3.2) hold，consider L(r(T))≽0，Θ ≽0，and Ri(t)≻0，there exists a solution Pi(t)∈Rn×n，∀i ∈S，satisfying

for each i ∈S，t ∈[0，T].

For notational simplicity，we define

As in (3.1)，for finite T ∈R+arbitrarily fixed，the set of SGCDRE is defined as

ProofWe follows the matrix decomposition method of theorem 2.1，then there exist two orthogonal matrices Mi∈Rn×n，Ni∈Rn×n，∀i ∈S such that

where Pi1(t)，Pi2(t)，Pi3(t)，Pi4(t)，Qi1(t)，Qi2(t)，Qi3(t)，Li1(t)，Li2(t)，L(r(T))11，L(r(T))12，L(r(T))22are all matrices with appropriate dimensions.By means of the relation (2.5)，it is easy to obtain that the Moore-Penrose pseudo inverse of E is

We directly use the transformations (2.5)-(2.9) and (3.6)-(3.10) to SGCDRE (3.1).Then the first eqation of (3.1) can be partitioned into

By the equation(3.1)，we get ΣrPi1(t)=(ΣrPi1(t))Tand Pi2(t)=0.Then，from the equation(3.11)，we obtain three equations as follows:

By the assumption H(3.1) to be seen，Ai3(t) ≡0 and the matrix Bi(t) is full of column rank，without loss of generality，we can assume that Bi2(t)≡0，∃t ∈[0，T].Then the equation(3.12) can be rewritten as

By the conditions of the theorem 3.1，using the transformations (3.7) and (3.8)，we can get that

where Ni=(Ni1Ni2)，Ni1is full-column rank with appropriate dimension.Having a careful observation to the system(3.13)，we can know that the equation(3.13a)has a solution ΣrPi1(t)on [0，T] with ΣrPi1(t) ≽0，∀t ∈[0，T]，guaranteed by [6]，then substituting it into (3.13b)，we could get the solution Pi3(t).By the assumption H(3.2)，we can use the similar method in[30] to deal with the equation (3.13c)，so we can get a solution Pi4(t) to the equation (3.13c).

From what has been discussed above，the theorem is proved.

Remark 3.1In particular，when Di(t) ≡0，Li(t) ≡0，and S = {1} in Theorem 3.1，we can see that the result can not be reduced to the result in [20].So (3.1) can be regarded as an extension of the GDRE in [20].

4.Application to Optimal Control

In Section 2，we know the system (2.1) has a no-impulse solution on [0，T]，∀i ∈S.In this section，we apply the above existence results to study the optimal control of Markovian jump linear stochastic singular system，and obtain the desired explicit representation of the optimal controllers for the optimal control problem with the finite horizon.First of all，We now give basic definitions and Lemmas before continuing our discussion，which will be used in the derivations of the main theorem.

The objective of the optimal control in this paper is to find the optimal control u*(·)∈Uadthat minimizes the performance index J(0，x0，r(0)，u，T).The optimal valued function is defined as

Definition 4.1The optimization problem is called well-posed if

-∞＜V(0，x0)＜+∞，∀x0∈Rn.

A well-posed problem is called attainable (with respect to x0) if there is a control u*(·) that achieves V(0，x0).In this case，the control u*(·) is called optimal (with respect to x0).

Lemma 4.1[16](Generalized Itˆo’s formula) Let x(t) satisfy

dx(t)=b(t，x(t)，r(t))dt+σ(t，x(t)，r(t))dω(t)，

and φ(·，·，i)∈C2([0，∞)×Rn)，∀i ∈S，be given.Then

where

Lemma 4.2Let f be a differentiable function such that f(t，x，i)=xT(t)ETPi(t)x(t)，where Pi(t) ∈Rn×nsatisfies the SGCDRE given by (3.1).Then，for the system (2.1) with u ∈Uad，the generalized Itˆo’s formula (4.1) can be written as

ProofBy the condition that ETPi(t)=(t)E，we can apply generalized Itˆo’s formula to xT(t)ETPi(t)x(t)，

where [···] does not affect the calculation result and can be omitted.Applying (3.1) to the above equation，we get (4.2).This complete the proof.

Lemma 4.3For arbitrary u ∈Uad，the cost functional defined in (2.4) is given by

where Γi(t)=:=(Mi(t)x(t)+Ri(t)u(t))TΓi(t)(Mi(t)x(t)+Ri(t)u(t))，with Pi(t) satisfying (3.1).

ProofFrom (2.4) we have that

Now，from Lemma 4.2，setting s=0 and t=T in (4.2)，we get that

where y =Mi(t)x(t) and ω =Ri(t)u(t)，which completes the proof.

Theorem 4.1Assume the SGCDRE admits a solution Pi(t)∈Rn×non t ∈[0，T]，and the finite horizon LQ optimal control problem (2.1)，(2.4) is well-posed.Then，the optimal control in the admissible class Uadis given by

where Ki(t)=(t)Mi(t)，i ∈S.Furthermore the minimum cost is given by

ProofThe proof is immediate from Lemma 4.3.

Remark 4.1Compared with[2]and[20]，although the method adopted here，to prove the sufficiency of solvability of SDCDRE for the well posedness of LQ problem，is the same，under the condition that Ri(t) ≻0，we get a different result in the case of linear stochastic singular systems with Markovian jumps.Unlike the standard stochastic system，the optimal control of stochastic singular systems with Markovian jumps is not unique.