基于最优网损的配电网重构
2021-01-07关海鹏赵秋霞迟美玲
关海鹏,赵秋霞,迟美玲
(运城学院 数学与信息技术学院,山西 运城 044000)
引言
配电网是人们直接用电的基本设施,它的结构体系庞大、错综复杂,运行的好坏直接影响着用户的体验质量。在系统正常运转的状态下,配电网中每条线路的日负荷情况皆有不同,负荷的极值时间也随之变化[1]。在这种情况下,对配电网进行重构可以有效地平衡负载、减少网损,以提高供电电压质量、减小经济消耗。因此,配电网重构技术对供电系统的运行以及民众的便利有着重大研究意义。
传统的配电网重构算法如遗传算法[2,3]、蚁群算法[4]等已经得到很好的应用。除此之外,还有其他算法的应用。臧志斌[5]、肖轩怡[6]等在潮流计算的基础上,采用启发式算法来确定径向配电网的最小损耗配置。吴霜[7]立足于启发式规则,结合模糊多目标方法对电网的配置进行优化。而谭辉[8]以能量最小损失为目标函数,结合用户的需求、当前的系统负荷,改变电网的切换序列,达到重构配电网的目的。陈莎[9]利用最小生成树Kruskal算法对配电网进行了重构过程中,首先利用初始网损权值求出最小生成树T,然后对该树的权值进行了重新计算,加入最小权值支路,更新迭代求出最小生成树。
根据图论理论,运用最小生成树算法对配电网进行优化重构,不仅是被应用最多的优化算法,更是适用于网络优化重构的算法。本文将最小生成树算法和潮流算法相结合,解决配电网重构问题。
1. 配电网的数学模型
传统电网采用的数学分析模型主要有非线性和线性两种,并同时依据优化算法求取最适合的解。目标函数的选取取决于解决问题的角度和算法的实质,主要有以下几种目标函数。
1.1 目标函数
(1)以网损最小作为目标函数:
(2)以均衡负荷作为目标函数:
(3)以开关控制次数最少作为目标函数:
(4)以提高电压质量为目标函数:

1.2 约束条件
(1)配电网重构后的网络依然为辐射状。
(2)配电网不能有孤岛。
(3)满足潮流计算方程。
(4)开关操作次数尽量减小。
(5)电流与电压约束。
式中,Ui,min和Ui,max分别为节点电压i的下上限;Ci为支路i流过的实际功率;Ci,max为支路i的功率最大负载值(变压器最大允许值与支路馈线相比较,取较小的值)。
1.3 潮流算法
潮流算法有很多种,本文选用的是前推回代法[10],该算法以馈线为基本计算单位,通过配电网的始端电压和终端负荷,求得各节点的电压分布。在计算前,需要先给支路进行编号[10]。本文应用该算法的前提条件为,假设三相辐射配电网是平衡的,用单相模型进行等值替代是成立的。
功率前推过程:

电压回代公式:
电压幅值的前推计算公式:
式中,Psi和Qsi分别为节点i的有功损耗和无功损耗;Ri为支路i的电阻值;PDi和QDi分别为节点i的有功功率负荷和无功功率负荷;Pi和Qi分别为节点的有功功率和无功功率;Xi为支路i的电抗值。
计算步骤如下:
Step1 进行初始化操作,迭代次数k=0,设置根节点电压。
Step2 根据已知的节点功率.从配电网的末端节点向根节点进行计算,要先计算子支路后计算父支路,其次利用功率前推公式计算配电网的潮流功率分布。
Step3 从网络的根节点出发,要先计算父节点然后计算子节点,再通过电压回代公式计算配电网的电压分布。
Step4 判别邻接两次电压差幅值的最大值max|ΔUi|与已知的收敛数值ε的大小.如果满足收敛条件,则停止计算;反之令k=k+1,然后返回步骤Step3。
2. 基于Kruskal算法的数学模型
Kruskal算法(克鲁斯卡尔算法),是在赋权无向连通图中,不断地选取权值最小的边加入集合。该算法的实质是贪心算法,由于要包含所有的顶点的数为n,所以总共要选择n-1条边。
2.1 目标函数
本文通过优化配电网络,以便改善配电网的经济性、安全性和可靠性。故对前面提到的以网损最小作为目标函数进行修正:
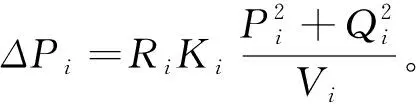
2.2 约束条件
(1)配电网重构后的网络依然为辐射状。
(2)配电网中不存在回路并且也没有孤立节点。
(3)切换操作的次数尽量减小。
(4)容量与节点电压约束。
满足潮流计算方程。
2.3 基于Kruskal算法的配电网重构实现过程
配电网重构是闭环设计,开环呈辐射状运行[11],因此可以把配电网看作是一个加权连通图,通过改变开关状态,调整网络拓扑结构,优化配电网络系统结构。陈莎[9]在整个重构过程中,支路权值加入过多,使得运算较为复杂且会造成运算的混乱,N次迭代下来,得出的最终结果并不一定是最优结果。因此本文将该步骤进行了改进,加入支路之后产生回路形成无向图,在此基础上再对权值进行重新计算并求出最小生成树,避免了权值混乱而求得的结果,使权值更加接近真实合理,得到更优化的结果。
本文在配电网重构过程中所采用的Kruskal算法不对其初始结构产生依赖性,可以有效地对配电网复杂的结构进行问题的寻优,从而可以得出,配电网重构问题的最优解。即可以看作是对某一明确的根节点,通过满足某一目标函数,探索配电网所对应的最小生成树过程。
首先假设整个配电网为一个赋权连通无向图G=
而Kruskal算法作为寻找最小生成树的主要算法之一,因为不限制初始结构,所以在配电网优化重构中被大量使用。该算法的操作步骤为:
Step1 在闭合所有开关的前提下,通过潮流算法计算潮流作为初始权值W(e0)。
Step2 利用Kruskal算法计算,寻找网络的初始最小生成树T(K),经过反复更新迭代,找出全网的最小生成树使配电网结构状态达到最优。具体步骤为:
Step2.1 根据初始权值W(e0)找到最小生成树T(0)并求出其目标函数minpL0。其中,树T(0)之外的线路权值不发生变化,但是要将它们按照从小到大的顺序依次放入队列Q中。
Step2.2 取出队首元素放入树T(0)中形成无向图G1;由于多加一条边产生了一个环路,所以要重新计算无向图G1的权值W(e1),并找到最小生成树T(1),求出其目标函数minpL1。
Step2.3 比较目标函数minpL0与minpL1的大小,若minpL0小,则令T(1)=T(0);若minpL1小,则将无向图G1中树T(1)之外的线路权值放到队列Q的尾端。
Step2.4 回到步骤Step2.2,直到队列Q为空,输出最小生成树T(N)。
3. 算例分析
3.1 算例1
该算例采用的是IEEE14节点电网系统对本文算法进行测试。该电网系统参数信息有馈线电压为12.66 kV,总有功负荷为2590 kV,无功负荷为j735 MVA,基准电压取10.5 kV。配电网的原结构方式如图1所示。
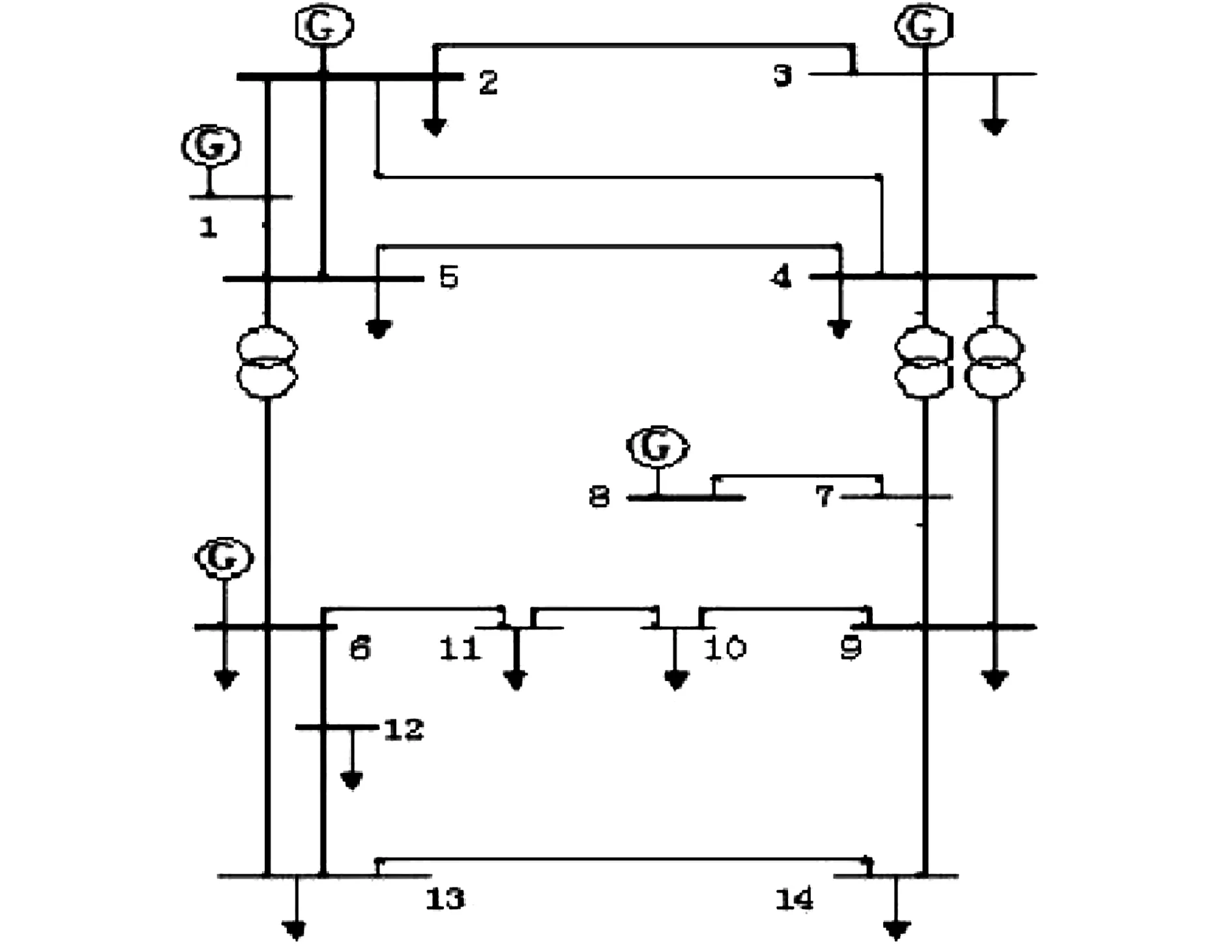
图1 IEEE14节点配电系统图
将图中的14个节点抽象成为网图中的14个节点,首选利用上述算法计算的电压分布,如图2所示。
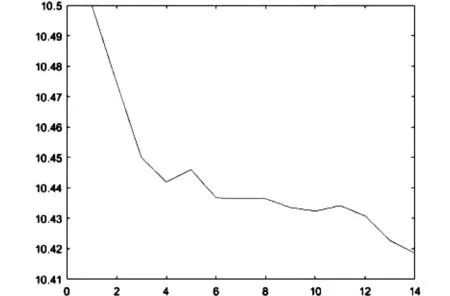
图2 IEEE14系统初始化潮流节点电压分布
由图中得出最低电压节点为14,电压值为10.4186 V。对IEEE14节点系统进行初始权值更新,同时每个节点的网损如表1所示。
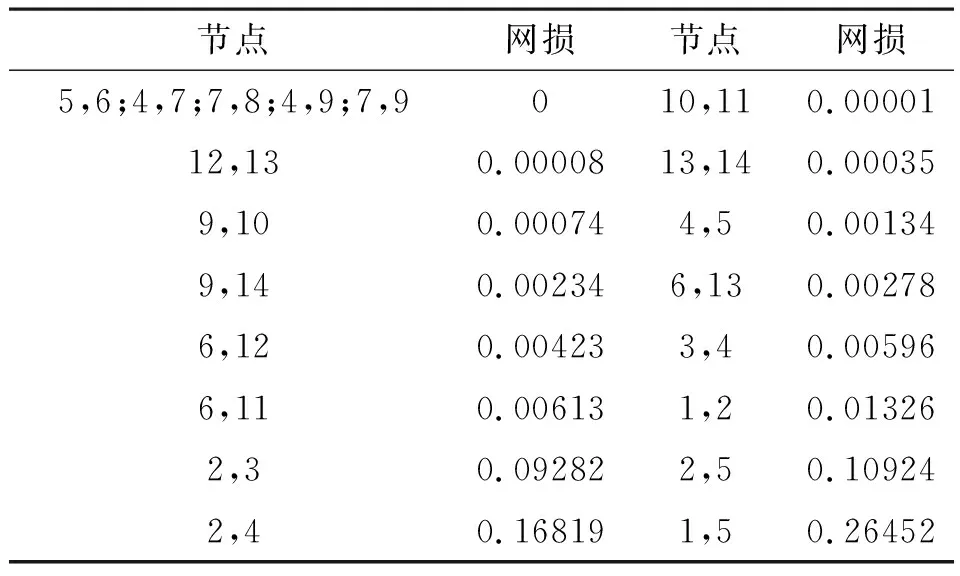
表1 IEEE14节点系统各支路初始网损
依据这些网损值,使用Kruskal算法进行重构,得出本算例系统所对应的如图3所示的系统初始最小生成树。
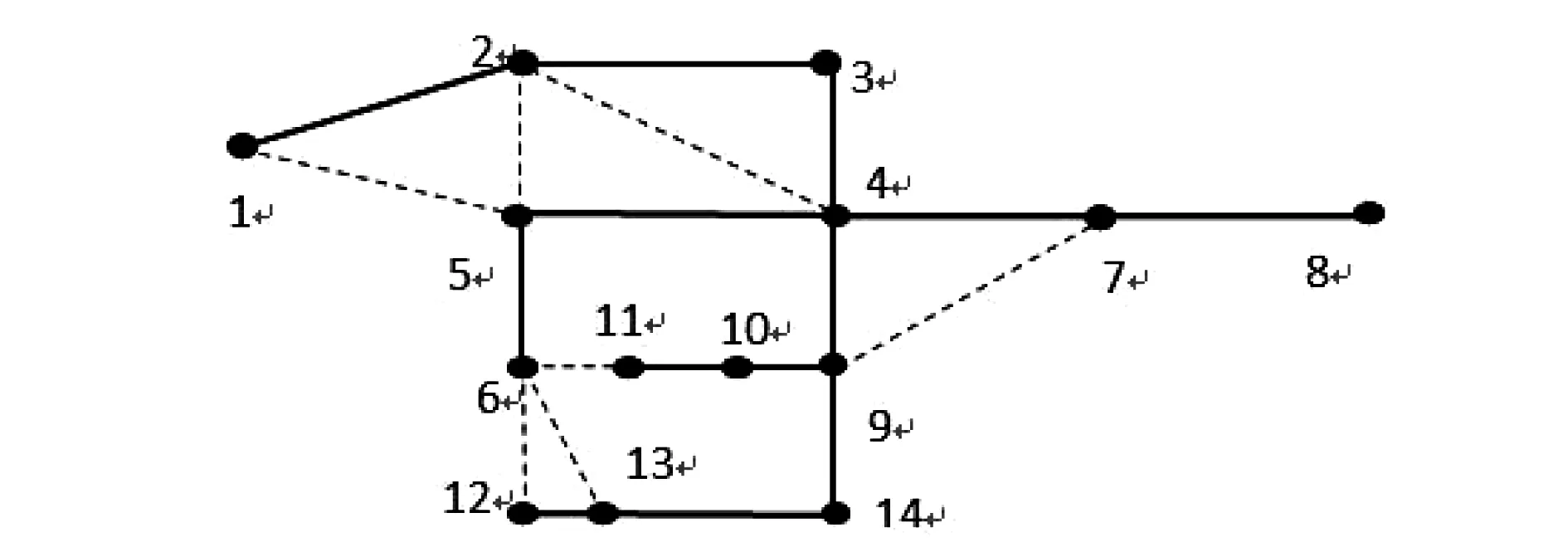
图3 IEEE14系统初始生成树
该初始生成树的网损是0.51241 MkW.利用Kruskal算法进行迭代更新,最后得出的最小生成树如图4所示。
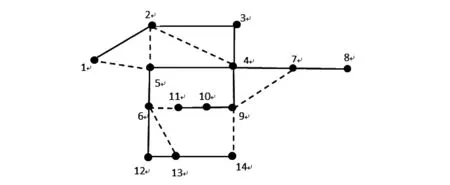
图4 IEEE14节点系统重构最小生成树
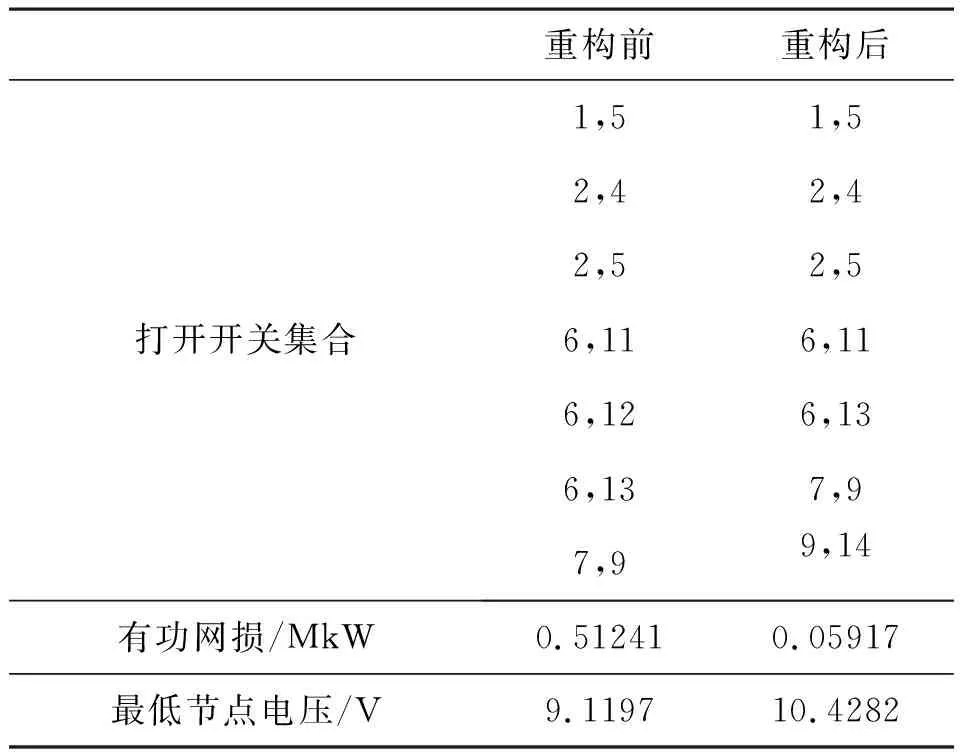
表2 重构结果比较
由表2可知,重构后的网损明显减小,最低节点电压有所提高,一定程度上改善了电压质量。
3.2 算例2
该算例采用的是IEEE33[12]节点电网系统,基准电压值取12.66 kV,三相功率准值取10 MVA,总负荷5084.26+j2547.32 kVA。配电网结构如图5所示。
其所包含节点的电压分布如图6所示。
由图6中得出最低电压节点为31,电压值为9.4949 V。对表3所示的IEEE33节点系统各支路初始网损进行权值更新。

图5 IEEE33节点配电系统图
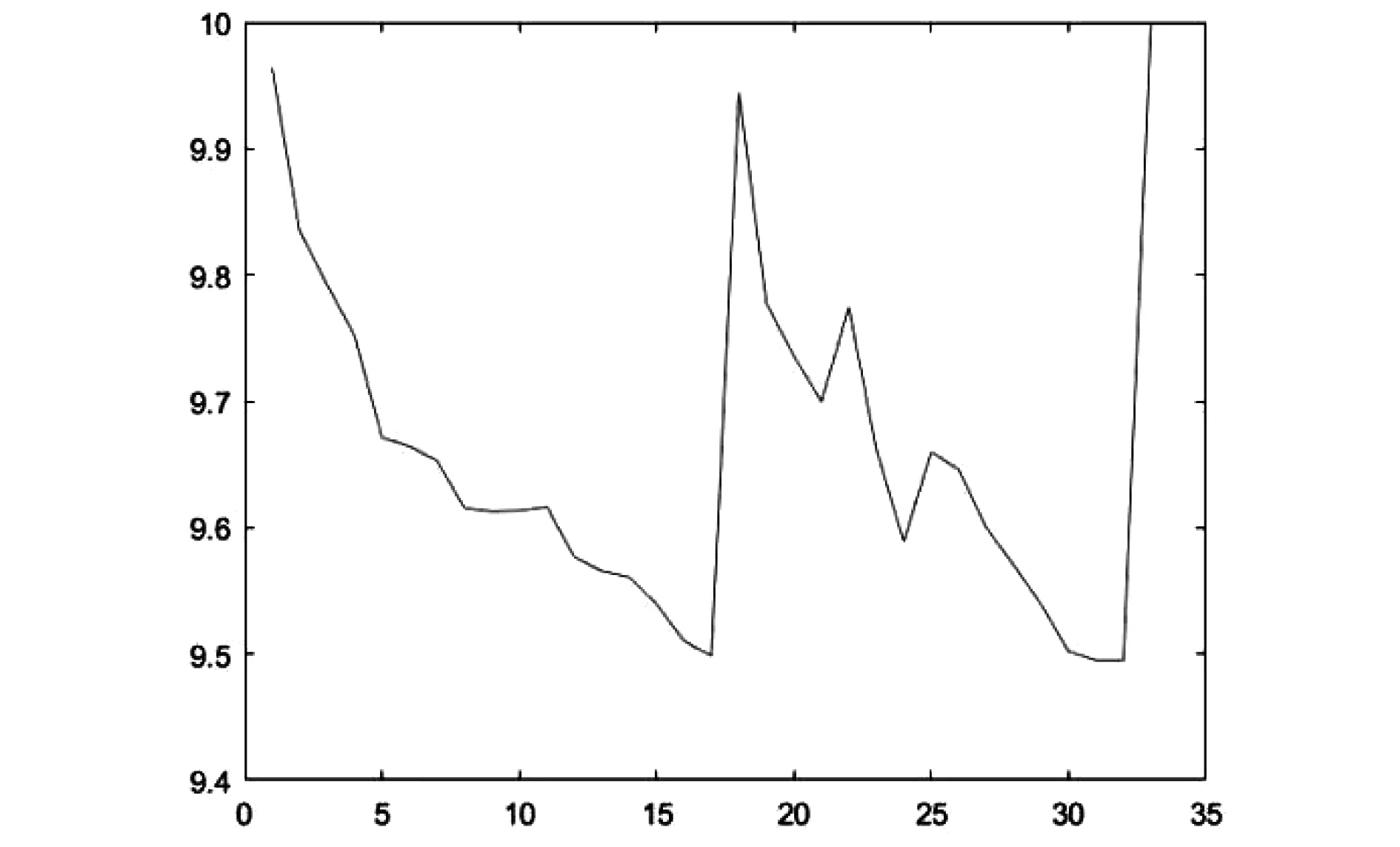
图6 IEEE33节点系统初始化潮流节点电压分布
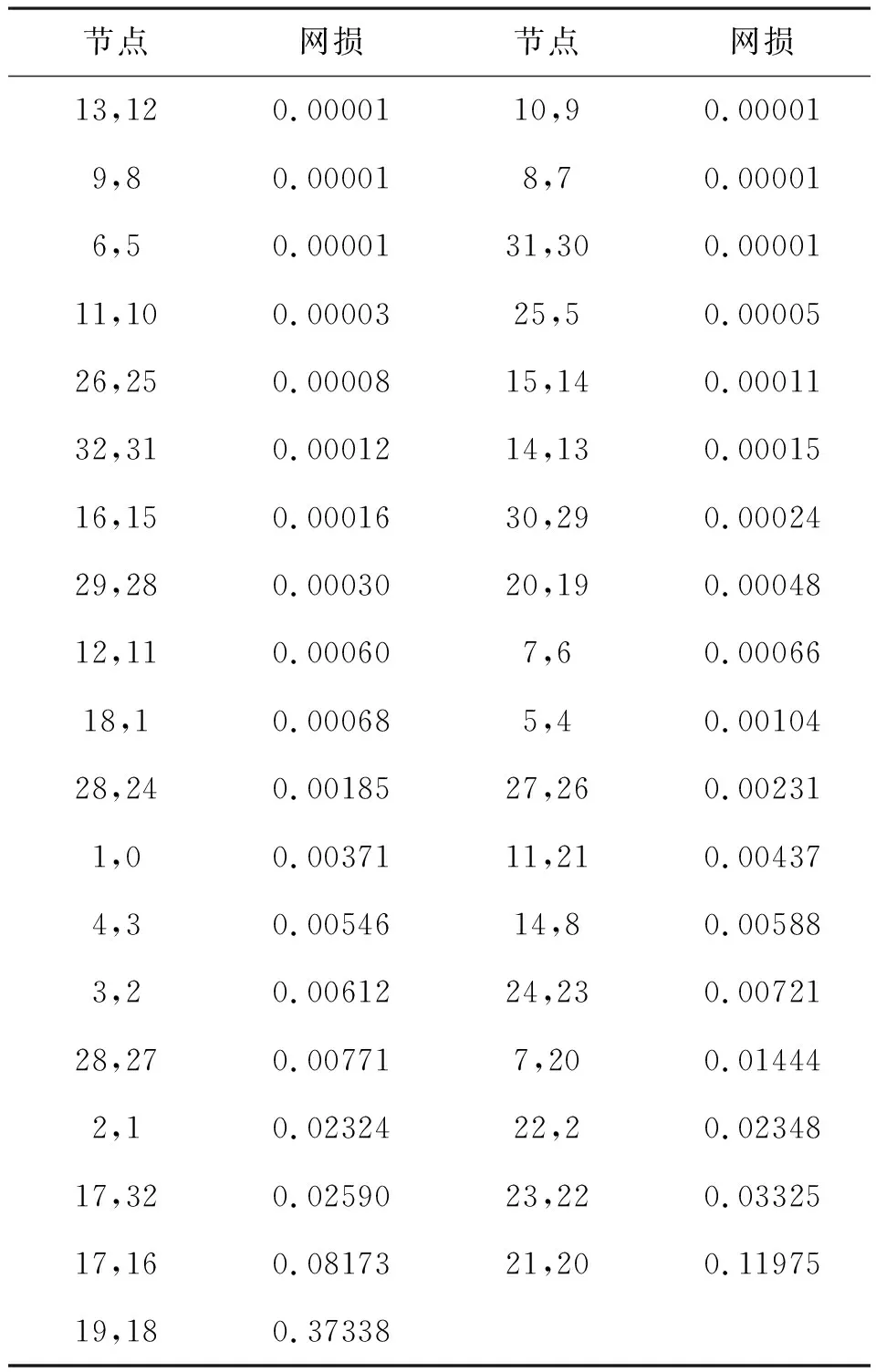
表3 IEEE33节点系统各支路初始网损
更新权值后使用Kruskal算法对网络进行初始化重构,得出系统的初始最小生成树,如图7所示。
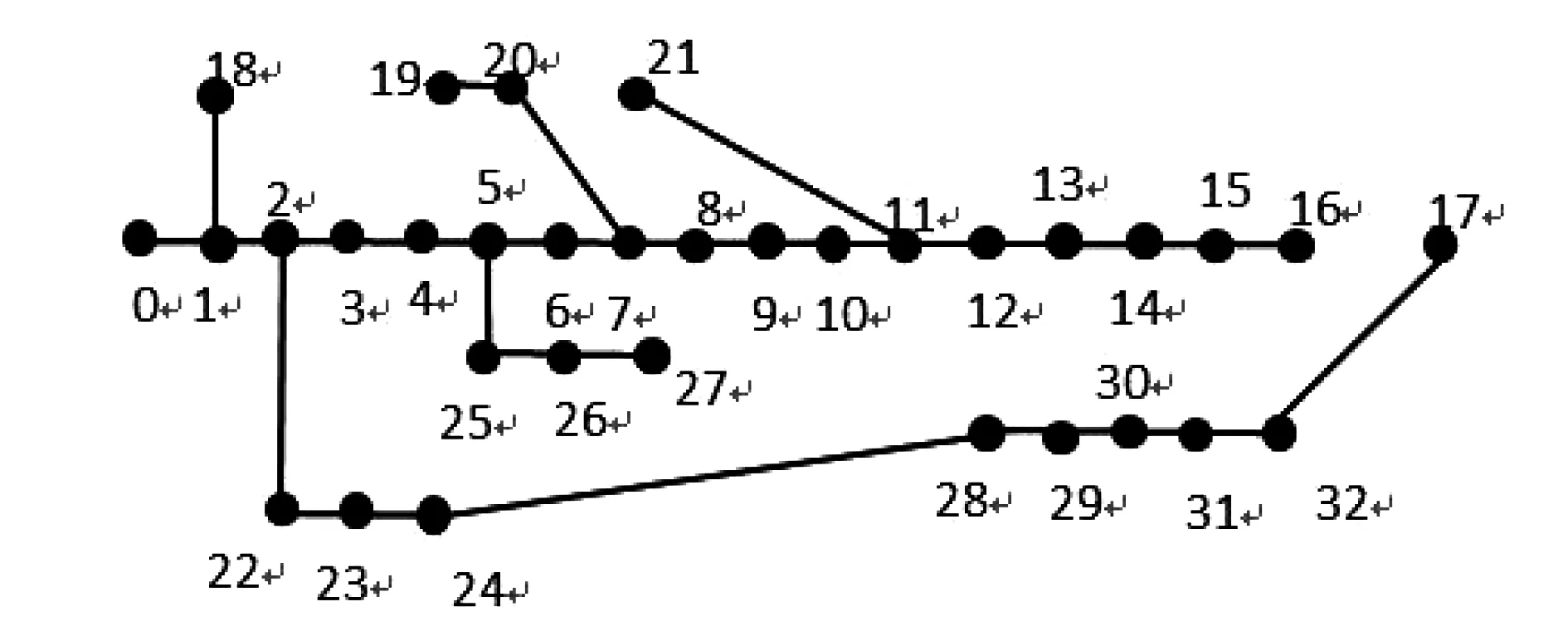
图7 IEEE33节点系统初始生成树
该初始生成树的网损是0.54876 MkW。利用Kruskal算法进行迭代更新,最后得出的最小生成树,如图8所示。
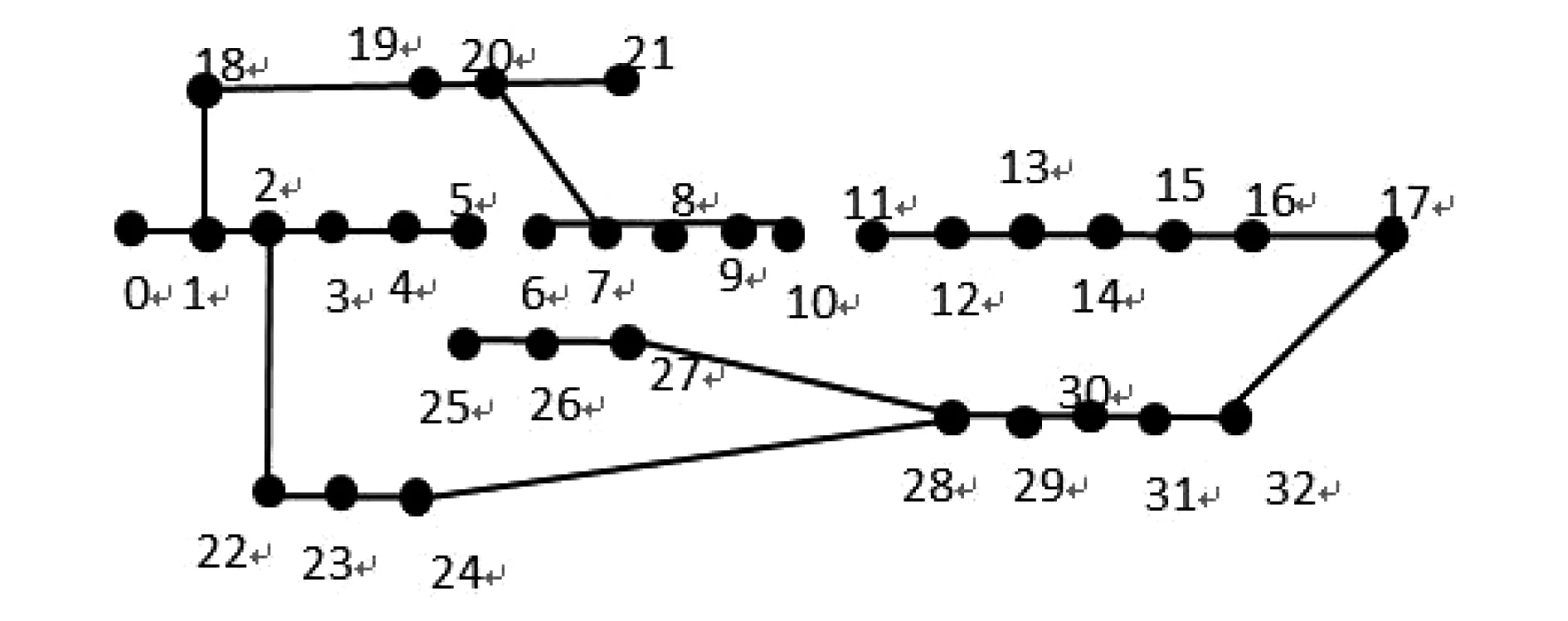
图8 IEEE33节点系统重构最小生成树
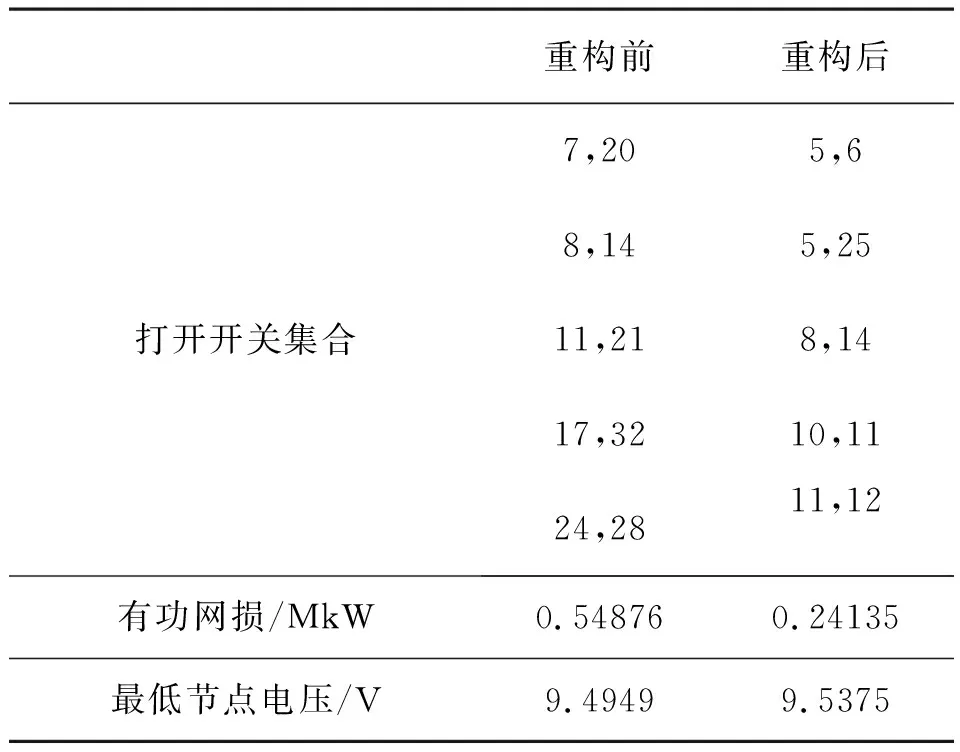
表4 重构结果
由表4可知,重构后的网损明显减小,最低节点电压有所提高,一定程度上改善了电压质量。
4. 结论
配电网重构主要有网络优化和故障优化两种重构方式。本文以网损最小为出发点来改善配电网的性能,属于网络优化的一种。研究结果主要包括:
(1)给出更加合理的权值。将配电网和图论联系起来,结合配电网特性,提出合适的赋权算法。在开关闭合的状态下,通过潮流计算对配电网进行初始赋值。
(2)基于最小生成树的Kruskal算法进行网络优化重构,计算网损,以网损最小作为目标函数,进行支路交换操作反复迭代更新,直至寻找出符合目标函数的最小生成树。
(3)通过仿真算例,对基于最小生成树算法的配电网重构方法进行验证,结果表明:配电网优化重构技术对电网线路消耗削减,对提高供电质量具有实际意义。
