可证安全的无证书指定验证者的签名方案

2021-01-07刘晓红

运城学院学报 2020年6期

刘晓红

(运城学院数学与信息技术学院，山西运城 044000)

Al-Riyami等人于2003年首次提出了无证书公钥密码体制的思想[1]，引起了学术界的广泛关注，许多新的无证书签名方案被相继提出[2-4]。1996年欧密会议上Jakobsson等人首次提出了具有指定验证者的签名方案[5]，它是指签名的人可以指定其签名的验证者，只有指定的验证者才能判断签名的正确与否，所以近年来不少指定验证者的签名方案被提出[6-8]。2001年亚洲密码学会上Boneh, Lynn和Shacam提出了一个短签名方案[9]，但他们是在超椭圆曲线上利用双线性对运算进行签名的，从而导致了昂贵的计算代价。

左黎明等人在Inv-CDH困难问题假设和随机预言机模型下提出了一种改进的高效无证书短签名方案并对其进行了安全性分析[10]。杨小东等人在标准模型下提出了一种安全的无证书签名方案[11]。李祖猛等人对樊爱苑等人提出的无双线性对运算的无证书签名方案进行了分析并改进[12]。在此基础上，本文提出了一个无双线性对运算，且具有指定验证者的可证安全的无证书签名方案，并在CDH和DLP困难问题假设以及随机预言模型下证明了该方案的安全性。

1. 预备知识

1.1 困难问题及假设

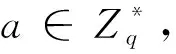
1.2 安全模型

对于无证书签名方案，我们一般考虑两种类型的攻击，一种是公钥替换攻击，指攻击者可以通过查询用户的公钥或者替换用户的公钥来伪造签名；另一种是恶意的KGC(秘钥生成中心)伪造攻击，指KGC事先知道要伪造的目标用户，然后根据其生成特殊的系统参数，最后伪造签名。

2. 新的无证书指定验证者的签名方案

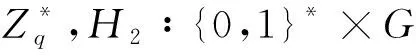
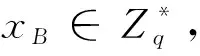
(3)签名阶段：设需要签名的消息为m，A计算σ=SAH2(m,xAPB),则签名为(m,σ，IDB)。

(4)验证阶段：B收到消息m的签名(m,σ,IDB)后，计算

σP=QAPAH2(m,xBPA)

是否成立确定签名的合法性,如果等式成立，则签名有效；否则拒绝。

3. 方案的安全性分析

3.1.正确性分析

xAPB=xAxBPpub=xBPA,

σP=SAH2(m,xAPB)P

=xADAPH2(m,xBPA)

=xAsQAPH2(m,xBPA)

=QAPpubH2(m,xBPA)

3.2 不可伪造性分析

证明：C在与A1交互的过程中试图解决CDH问题，即输入(P，aP，bP),目标是计算出abP，并且在下面游戏中充当挑战者与A1进行交互。在证明中假设A1是验证者B，此时xBPi为固定值，如果B不能伪造签名，则任何人都不能伪造签名。以下是攻击的几个阶段：

(1)C建立系统参数params={G，q，P，Ppub，H1，H2}。其中Ppub=sP,将参数params发送给敌手A1，保密系统的主密钥。

(2)查询阶段：设A1攻击的目标ID为ID*，C要维护以下列表来保存询问结果：

PK—list(IDi,xi,Pi)
H1—list(IDi,Pi,Qi)
H2—list(Pi,mi,h)

SK—list(IDi,xi,Di)

①公钥查询

A1向C询问IDi的公钥，若在公钥列表中已经存在，则C返回Pi给A1，如果不存在，并且IDi≠ID*，则C随机选择xi，计算Pi=xiPpub,并将(IDi,xi,Pi)加入到PK列表中。如果IDi=ID*，则C随机选择a，计算Pi=aPpub，并将(IDi,⊥,Pi)加入到PK列表；

②H1查询

A1询问IDi部分私钥，C先检查H1列表，当对应的(IDi,Pi,Qi)在H1列表中时，则将其返回给AI，否则根据公钥查询先建立PK列表，然后随机选择ri，令Qi=ri,并将(IDi,Pi,Qi)加入到H1列表。

③部分私钥查询

当A1向C询问IDi的私钥，并且IDi≠ID*时，C首先检查已建立的SK列表，若(IDi,xi,Di)在列表中，则将其返回，否则,建立PK列表和H1列表，然后计算Di=sri，并将(IDi,xi,Di)加入到SK列表；如果IDi=ID*,则终止。

④查询

当AI向C询问消息mi所对应的H2时，C首先检查(Pi,mi,hi)是否在H2列表中，若存在，则将其返回，否则当mi≠m*时，C随机选取ui，计算hi=uiP返回给AI，并添加(Pi,mi,hi)到H2列表中，当mi=m*时，选择b，计算hi=bP返回给AI，并添加(Pi,m*,⊥)到H2列表中。

⑤公钥替换查询

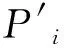
⑥签名查询

当AI想要询问IDi对消息mi的签名时，首先检查IDi是否等于ID*。

(a) 如果IDi≠ID*，则C首先查找IDi的私钥和mi对应的hi，然后计算σi=xiDihi。

(b) 如果IDi=ID*,则算法终止。

⑦签名验证查询

当A1想要验证签名(mi,σi,IDB)是否正确时，C首先查找H1列表，PK列表和H2列表，找到IDi相应的Qi和Pi以及mi、Pi对应的hi，然后计算σiP,并验证等式σiP=QiPihi，如果等式成立，则返回‘1’，表示通过验证；否则返回‘0’，表示签名无效。

(3)伪造阶段

如果攻击者AI成功伪造了签名(ID*,m*,σ*)，且IDi≠ID*，则算法失败，如果IDi=ID*，由验证等式：

σ*P=QiPiH2(xBPA,m*)

=ri·asP·bP=absriPP

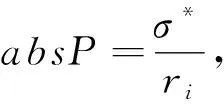
概率分析：要使得攻击成功，须满足下面三个条件：

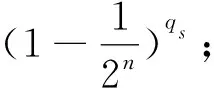
②攻击者以ε的概率生成一个有效的且没有被询问过的签名(mi，σi,IDB);

证明：给定一个随机的DLP问题实例(q，P，aP),算法C的目的是计算获得a，同定理1的证明，C试图以AⅡ为子程序解决DLP问题，并充当游戏中的挑战者。游戏开始时，C设置系统参数为params={G,q,P,Ppub,H1,H2}，其中Ppub=sP，然后将系统主密钥s和参数params发送给AⅡ，设IDA,IDB是目标签名者和目标验证者，根据定义，攻击者AⅡ拥有系统的主密钥，但不能替换用户的公钥，同样，在证明中AⅡ假设是验证者B，此时xBPA为固定值，如果B不能伪造签名，则任何人都不能伪造签名，AⅡ同定理1一样进行PK、H1、H2及SK询问。

签名询问：

当AⅡ想对消息mi进行签名询问时，执行

(a)当IDi=ID*时，拒绝，终止游戏；

(b)当IDi≠ID*时，首先进行SK询问、H1询问和H2询问，然后计算ti=xisrihi，σ=tiP.返回(mi,σ,IDB)给AⅡ.

伪造签名阶段：

AⅡ成功伪造了签名(m*,σ*,IDB)，即成功找到了t*，使得

σ*=t*·s·H2(m*，xBPi)

如果IDi≠ID*，则算法失败，如果IDi=ID*由验证等式：

σ*P=QAPAH2(m*,xBPi)，

得

t*·s·H2(m*,xBPi)·P=ri·a·s·P·H2(m*,xBPi)从而a=t*/ri.解决了离散对数问题。

概率分析同定理1，得证。