考虑共享不确定因素的应急设施最大覆盖选址模型

于冬梅，高雷阜，赵世杰

(1.辽宁工程技术大学 优化与决策研究所，辽宁 阜新 123000; 2.辽宁工程技术大学 运筹与优化研究院，辽宁 阜新 123000;3.北京航空航天大学 数学科学学院，北京 100191)

0 引言

应急设施选址是长期战略性决策布局问题，选址分配网络面临不确定决策环境和潜在的中断风险，其选址布局决策的稳健性直接影响应急救援的效率，在一定程度上对应急服务质量和应急资源的合理分配具有根本性影响[1]。灾害发生之前的应急设施选址布局决策是提升应急服务质量的重要环节，由于选址决策的长期艰巨性，选址过程中的诸多不确定因素增加了决策的难度，加之应急设施在突发灾害事件下失效(或损毁)的情况愈演愈烈，极大的降低了应急设施的可靠性和服务的质量。因此，必须在进行应急设施选址决策时就考虑整个系统的稳健性和不确定性，将突发事件可能造成的伤害降到最低[2～4]。

应急设施选址属于设施选址问题的范畴，覆盖模型在应急设施选址中的应用和研究极为广泛，其最早可以追溯到Toregas的集覆盖选址模型[5](Location Set Covering Problem，LSCP)和Church and ReVelle提出的最大覆盖选址模型[6](Maximal Covering Location Problem，MCLP)。基于覆盖选址问题，诸多学者根据模型不同的限定条件对模型进行扩展和改进，尤其是考虑不确定因素的覆盖模型引起一大批学者的广泛关注。随机规划[7]采用随机变量描述不确定性，通常假设随机变量遵循某种分布，文献[8]假定了若干随机突发事件的情景，建立基于随机规划的应急设施选址与资源配置模型。Guzmáan等[9]基于模糊规划思想构建了约束条件中含有梯形模糊数的应急物资储备库选址模型，而模糊规划采用模糊变量和模糊集合分别描述不确定性和约束条件，将约束条件的满足程度定义为隶属度函数，模糊隶属度函数的确定往往有一定的主观性。鲁棒优化方法[10]对不确定性的刻画方式易于实现，它将数据的不确定性用有界闭且凸的集合描述，通过求解不确定问题的鲁棒对应求得扰动意义下的鲁棒解，该解对于集合内不确定数据的任意取值都满足约束条件[11,12]，在处理不确定因素时展现了较好的效果。鲁棒决策方案能在不确定参数变动的情况下，仍保持较高的质量，包括解的可行性和目标水平。Vatsa等[13]考虑应急服务的不确定性，基于最小最大鲁棒优化方法建立多阶段最大覆盖选址混合整数规划模型，并设计Benders分解方法实现模型的求解，Murali等[14]针对大规模生物恐怖袭击问题，考虑需求的不确定性建立无容量限制的最大覆盖选址模型，并设计选址-分配启发式算法对模型予以求解。文献[15,16]分别研究了基于鲁棒优化的不确定需求下的选址模型，更多考虑不确定因素的覆盖选址模型参见[17～19]。已有考虑不确定因素的最大覆盖选址模型及扩展模型中，未充分考虑约束和目标中同时存在共享不确定因素的情形，并且都假设建立的设施将一直完全可靠的正常运行。但囿于自然灾害、事故灾害、恐怖袭击及其他不可抗因素而使得设施存在中断的风险，如果设施中断，其服务的需求点需由距离更远的设施为其提供应急服务，选址网络的拓扑结构也会因此改变，将严重影响整个系统的服务效率和响应能力。因此，在选址阶段就对设施可能中断的情景予以考虑，保证设施一旦中断应急服务系统仍能良好运行。

综上，考虑不确定因素的覆盖选址研究鲜有文献考虑需求点的共享不确定需求及设施中断对选址决策的影响。基于此，本文扩展MCLP模型，基于不确定决策环境和最大覆盖响应，建立共享不确定需求和服务能力有限的可靠性应急设施选址优化模型，降低不确定因素诱发的风险，使应急设施选址决策具有更好的鲁棒性，从而合理配置资源，提高应急设施的可靠性和抵御风险的能力。此问题是MCLP的拓展，较高的算法复杂度至使精确算法求解较困难，本文利用具有较好优化求解性能的改进灰狼优化算法对模型予以求解，并通过算例仿真实验验证模型及算法的有效性和可行性。

1 考虑共享不确定因素的应急设施最大覆盖选址模型

1.1 鲁棒优化模型

则标准LP写为

maxcTx

-yj≤xj≤yj,∀j∈Ji

l≤x≤u,y≥0

maxcTx

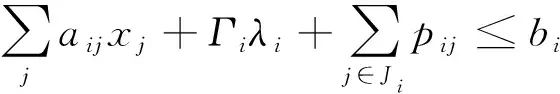
-yj≤xj≤yj,∀j∈Ji

lj≤xj≤uj,∀j∈Ji

yj,λi,pij≥0,∀j∈Ji

1.2 问题描述

基于不确定和中断决策环境，从应急服务质量的视角出发，在设施中断及共享不确定需求的情形下，确定应急设施点的位置，需求点在各个应急设施之间的分配以及选址-分配网络的拓扑结构。

应急服务质量是突发灾害事件下衡量救援效果的重要因素，引入应急设施选址中的服务质量覆盖函数，刻画需求点的覆盖水平(因变量)与距离，即应急设施响应需求点的距离要求(自变量)的数学关系式。通过需求点被提供覆盖服务水平与设施点和需求点之间的距离函数关系，刻画出应急设施的覆盖服务质量，进而保证选址决策的科学性，引入如下指数型非线性覆盖函数[21]。

(1)

式中，dij表示第i个应急设施到达第j个需求点的距离，ds为需求点获得应急设施覆盖的最小临界距离，du为需求点获得应急设施覆盖的最大临界距离，a=dij-ds，ds≤du，k，m为刻画应急设施为需求点提供服务的敏感程度因子。

1.3 数学模型

(2)

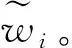
s.t. (3)～(11)

(12)

由于式(12)中含有内层最大化问题

基于不确定集合U，引入对偶变量σij和αj，将其转化为

基于强对偶性，得到对偶问题为

aiPijrf(dij)Zijr,σij,αj≥0,∀i∈I,j∈J}我们通过引入辅助变量t将最大化问题转化为最小化问题，得到鲁棒对应模型

s.t. (3)～(11)

σij+αj≥aiPijrf(dij)Zijr,∀i∈I,j∈J,r∈K

t,σij,αj≥0,∀i∈I,j∈J

γi+θu≥aiZijr,∀0≤i≤I-1,0≤j≤J-1

γi,θu≥0,∀0≤i≤I-1

其中γi，θu为对偶变量。

综上，考虑共享不确定需求的应急设施最大覆盖选址决策数学模型为

σij+αj≥aiPijrf(dij)Zijr,∀i∈I,j∈J,r∈K

γi+θu≥aiZijr,∀0≤i≤I-1,0≤j≤J-1,0≤r≤R-1

(3),(4),(5),(6),(7),(8),(9),(10),(11)

t,σij,αj≥0,∀i∈I,j∈J

γi,θu≥0,∀0≤i≤I-1

上述考虑共享不确定需求的应急设施最大覆盖选址优化模型是一个非线性混合整数规划模型，不易求解。为了求解所建立优化模型，利用具有较好优化性能的IGWO对模型予以求解。

2 改进灰狼优化算法

灰狼优化算法(GWO)[22]是一种群体优化搜索算法，其寻优思想是模拟灰狼群体的捕食行为和其群体内部的等级制度，通过模拟狼群追踪、围捕及攻击猎物等行为过程实现迭代寻优的目的。GWO具有操作原理简单、易于实现、调整参数个数少及搜索能力强等特点[23～25]，自被提出后得到广泛研究和应用。为避免算法在迭代过程中陷入局部最优，充分发挥GWO较好的寻优性能，将混沌映射引入算法中，利用混沌搜索所特有的遍历性、规律性和随机性等特点，增强算法的全局搜索能力，设计一种改进灰狼优化算法(IGWO)，实现所构建优化模型的求解。

IGWO将猎物位置映射为搜索空间中的点，灰狼个体位置的优劣度量优化的目标，引入Chebyshev混沌映射，对灰狼个体的整个寻优区间进行搜索。迭代过程中，我们利用具有较好遍历性和互不相关性的Chebyshev混沌映射对灰狼个体进行一定次数的混沌遍历，以迄今为止当前代个体产生的最优解作为混沌映射产生均匀分布的混沌初始值，位于狼群最高3个层级的灰狼α、β和δ为由高至低位置最好的3个解并以此判定猎物的位置，其余灰狼个体ω以所判定的猎物位置为依据，计算二者之间的距离，全方位实现对猎物的逼近和包围等行为操作。利用式(13)刻画灰狼个体与猎物之间的距离，灰狼个体位置的更新通过式(14)刻画。

D=|C·Xp(t)-X(t)|

(13)

X(t+1)=Xp(t)-A·D

(14)

式中，D表示灰狼个体与猎物之间的距离，XP(t)表示猎物在第t代的位置，X(t)表示灰狼个体在第t代的位置，X(t+1)表示灰狼个体更新后的位置。常数向量A和C由式(15)和式(16)确定。

A=(2r2-1)a

(15)

C=2r1

(16)

式中，r1和r2在[0,1]区间内随机产生，a在迭代过程中从2线性递减至0。

在迭代过程中，由α、β和δ对猎物位置予以定位和评估，以此为标准，计算种群内其他个体与猎物之间的距离，并全方位实现对猎物的靠近、围攻等行为操作，将获得的最好的3个位置求平均，进而更新搜索到的位置。灰狼群体中个体跟踪猎物的数学描述按式(17)～(22)确定群内个体与α、β和δ的距离，从而依据式(23)去判断个体向猎物移动的方向。

Du=|C1·Xα(t)-X(t)|

(17)

Dβ=|C2·Xβ(t)-X(t)|

(18)

Dδ=|C3·Xδ(t)-X(t)|

(19)

X1=Xα-A1Dα

(20)

X2=Xβ-A2Dβ

(21)

X3=Xδ-A3Dδ

(22)

(23)

下面给出IGWO求解所构建模型的实现步骤。

Step1相关参数设置：建立应急设施的个数P，预设服务质量水平Lr，在j处设立设施的最大容量cj，每个需求的扰动比例ai，每个设施的损毁概率qj，设施级数R，不确定水平参数Γi，需求点获得应急设施覆盖的最小和最大临界距离ds和du，覆盖函数中应急设施点为需求点提供服务的敏感程度因子k，m。

IGWO中设置的参数有：种群规模NumSA=20,a=2-1×(2/Maxcycle)，Maxcycle为最大循环次数，最大混沌搜索次数MaxIter_chaos=100，最大迭代次数NummaxIter=200。

Step2种群搜索体的初始化：随机初始化灰狼个体初始位置，生成一个20×(2×(I-1))的矩阵，矩阵中每行代表一个灰狼个体，每相邻两列表示一个应急设施的位置。

Step3计算初始种群个体的适应度值，并比较大小确定出当前种群中的适应度值与需求点之间的对应服务分配、排在前3名的最优个体位置Xα，Xβ,Xδ及与之相应适应度值，同时将该适应度值和相应个体分别赋值给全局最优适应度值和最优个体。

Step4IGWO的行为操作：依据式(17)～(19)计算灰狼其他个体与Xα，Xβ,Xδ的距离大小，并依据式(20)～(22)更新每个灰狼个体的位置，同时分别更新3个参数a，A，C，依据式(23)评估新位置。

Step5计算当前新种群个体的适应度值，标识当代种群中的最优个体和相应适应度值，将其与全局最优适应度值比较，若优，替换原全局最优适应度值，同时替换相应个体。反之，二者保持不变。

Step6混沌搜索过程：①从当前代灰狼种群中随机选一个个体作为混沌映射的初始位置，并将其转化为混沌变量；②将混沌变量代入混沌映射并增加一定的随机扰动产生新的灰狼位置；③将新的灰狼位置转化为优化变量并计算适应度值；④将混沌搜索所得灰狼新个体与被替换灰狼个体比较，若新个体适应度值优于原个体的适应度值，则以该新个体位置替换原灰狼个体，反之则保持不变；⑤将灰狼新个体与当前全局最优个体比较，若优于全局最优适应度值，则替换，否则原全局最优适应度值保持不变；⑥对混沌搜索次数MaxIter_chaos进行判断，若达到最大搜索次数，则跳转执行Step7；反之混沌迭代次数加1，并跳转执行①。

Step7终止准则：判断迭代是否达到种群最大迭代次数NummaxIter。若达到，输出全局最优适应度值和最优个体，对应应急设施的位置和各应急设施与需求点之间的覆盖服务关系，否则，迭代次数增加1并跳转执行Step4。

3 算例分析

为验证所构建模型及算法的可行性，基于文献[26]中的来自美国49个城市节点的数据进行算例仿真实验，其中49个城市节点的供应网络是以美国48个州首府和华盛顿特区作为城市节点，在设施损毁及共享不确定需求的情形下，基于49个城市节点网络确定8个拟建设施点的位置及需求点在各个设施之间的分配，实现整个供应网络的覆盖需求量最大。利用Matlab 2015a编程并执行算法，在Intel(R)，Core(TM) i7- 6500U CPU，2.50 GHz，8.00 GB内存，Windows10操作系统的PC机上执行算法。

每个应急设施能够设立的最大容量cj[4000,5000]在内随机产生，预设服务质量水平Lr在[0.7,0.9]内随机产生，每个需求点的需求名义值wi在[80,100]内随机产生，扰动量的比例为5%，不确定水平参数Γi=0,10,15,20。需求点获得应急设施覆盖的最小临界距离ds在[560,600]内随机选取，最大临界距离du在[2500,3000]内随机选取，覆盖函数中应急设施点为需求点提供服务的敏感程度因子k和m分别在[0,0.5]和[2,5]内随机产生。种群规模NumSA=20，最大迭代次数NummaxIter=200。

鲁棒控制参数Γi是衡量决策者风险偏好程度的重要指标，Γi的取值越大说明决策者在面对需求扰动时选址决策的态度越保守，反之越冒险。基于文献[26]的研究结果，设施级数R的变化不会对最优选址方案产生影响，因此，本文直接考虑3级设施选址分配。在规模及模型的相关参数设置相同的条件下将GWO与IGWO的求解结果进行对比，在损毁概率qj=0.1时，比较不同的Γi下，算法执行时间、覆盖需求量及最优目标值相对误差见表1。

表1 不同鲁棒水平下应急设施覆盖质量的结果

从表1的计算结果可以看出，考虑同一中断概率，随着Γi的增加，最优目标值对Γi具有较高的敏感性，当Γi=0时，此时鲁棒模型等价于需求确定的名义模型，Γi越大，得到的解越为保守。因此，通过调控不确定水平Γi，可以调节解的鲁棒性，不同决策者可以根据风险偏好控制解的鲁棒性，避免过度乐观或过度保守。

在鲁棒控制水平一致的情形下，Γi=15，研究应急设施覆盖选址网络在抵御中断风险时的表现，比较不同中断概率下的覆盖选址结果，基于IGWO求解的计算结果见表2。

表2 不同中断概率下选址优化的结果

从表2的计算结果可以看出，在同一鲁棒控制水平下，中断概率越大，选址网络受到的冲击越大，覆盖总需求量减小。当决策者考虑中断风险趋于乐观时，设计的选址分配网络更精益，覆盖服务质量较好，当决策者考虑中断风险趋于悲观时，设计的选址分配网络更保守，抵御中断风险的能力较强。

进一步分析不确定决策环境对选址-分配的影响，基于上述49个节点网络，以可视化的形式给出不同不确定鲁棒水平下应急设施选址-分配网络的拓扑结构和应急设施的覆盖范围，如图1～图4所示。图1～图2是针对49个节点网络，基于应急设施不同不确定鲁棒水平组合Γi=10,20，利用IGWO确定8个应急设施的选址-分配网络的拓扑结构。图3～图4展示了不确定鲁棒水平Γi=15时，中断概率qj=0.1,0.2时应急设施选址-分配网络的拓扑结构。

以上对需求点应急资源需求的不确定鲁棒水平和中断概率进行不同的设置，得出不同选址-分配网络的拓扑结构。图中实心圆点表示需求点的位置，星形表示选定应急设施点的位置，星形与圆点之间的连线表示对应的资源分配，虚线圆圈表示应急设施覆盖相应需求点。上述结果展现了不同的鲁棒水平与中断概率使应急设施选址-分配网络的拓扑结构截然不同，不同需求点获得应急服务的覆盖半径是不一致的，各应急设施点在不同的选址网络拓扑结构下实现最大质量覆盖。因此，在抵御不确定因素和中断风险时，决策者需基于不同的风险偏好和具体实际在系统成本和稳健性之间作出相应的权衡考虑，进而确定应急设施的选址分配方案。

图1 Γi=10时选址-分配网络的拓扑结构

图2 Γi=20时选址-分配网络的拓扑结构

图3 qj=0.1时选址-分配网络的拓扑结构

图4 qj=0.2时选址-分配网络的拓扑结构

4 结论

本文为给相关决策者在不确定环境下设计具有鲁棒性的应急设施选址布局决策提供模型和方法支持，对考虑共享不确定因素的覆盖选址模型进行研究。建立可靠性应急设施最大覆盖选址优化模型，基于Bertsimas and Sim的鲁棒优化方法将其转化为鲁棒对应模型，设计IGWO对模型求解并给出应急设施选址-分配网络的拓扑结构。算例仿真实验结果表明，中断因素和共享不确定需求因素影响应急设施的选址决策，并影响应急设施的服务质量。决策者可基于对不确定因素的风险偏好程度选择最佳的不确定水平，以获得最优的服务满意度和选址分配方案，为相关决策者提供建议和决策支持。