基于k-means聚类与粗糙集算法的指标筛选方法研究
2021-01-07张立军高春晓
张立军,高春晓
(湖南大学 金融与统计学院,湖南 长沙 410079)
0 引言
在综合评价问题中,运用恰当的方法进行指标筛选是不容忽视的重要环节,如果筛选出的指标体系不能系统全面地反映评价对象的特征,就会影响到最终的评价结果。粗糙集方法依靠其特有的数据挖掘和知识发现功能,能处理不精确、不确定、不完整的信息,具有较强的鲁棒性和可操作性[1]。
目前,作为一种指标定量筛选的方法,利用指标间的某种相关性对评价指标进行筛选的方法得到了广泛的应用,这类方法能够剔除信息重叠的部分指标。通过相关性分析剔除信息重复性指标的方法主要有:
依据指标两两之间的相关程度删除信息重复的指标,一是根据相关分析或偏相关分析剔除相关系数和偏相关系数比较高的部分指标。如张昆、迟国泰结合相关系数和粗糙集筛选出了生态评价指标体系[2]。陈险峰借助模糊隶属度、差异性分析、相关性分析、信度与效度检验、稳定性与贴近度等技术指标探讨了产业集群竞争力评价环节中的指标遴选问题[3]。二是利用互信息剔除反映信息重叠的指标[4]。互信息是利用信息熵测度指标间依赖程度的工具,属于信息论研究方法。互信息的大小能够反映指标相关性的强弱,互信息越大,关系越密切,该方法通常需要结合其他方法剔除相对不重要的指标。上述方法仅仅能够度量两个指标相互之间的相关性,并不能完全反映指标集内部的相关性,因此不能有效地降低指标集间的信息重叠。
(2)结合非参数统计、数据挖掘等理论分析指标间的相互关系,剔除冗余指标。如石宝峰、迟国泰等利用聚类方法分析每一类内相关程度高的指标,仅保留每一类中最重要的指标,从而间接减少指标间的重复信息[5]。又如王惠文等利用Gram-Schmid变换,构造正交的“主基底”,在尽量多的保留原始数据信息的情况下,排除所有的冗余变量及重叠信息[6]。再如侯娜等利用粗糙集约简思想判断灰色聚类结果的影响,筛选出的指标能显著影响样本分类的最终结果[7]。类似的,赵焕焕等利用灰色关联分析的思想方法,构建了一种区间粗糙数多属性决策方法[8]。这些研究利用客观数据缩减了指标间的重复信息,但均忽略了对指标实际意义的考量。
针对现有方法的不足,本文提出了一种基于k-means聚类与粗糙集相对约简原理的指标筛选方法,由样本的空间分布密度得到改进的初始聚类中心点,进而实现基于k-means聚类算法的数据离散化过程,再由知识的相对约简方法求解约简的指标集,该方法既能够对多余信息进行属性约简,又保证了指标的实际含义。
1 基于粗糙集理论的属性约简方法
1.1 连续属性离散化
由于粗糙集的学习算法仅可以对离散数据的决策表进行处理,因此将连续属性离散化就成为数据预处理的关键问题,其效果好坏直接影响数据分析结果。
目前,国内外学者已经针对连续属性的离散化提出了一些高效通用的方法,根据是否利用类信息,离散化方法主要分为无监督方法和有监督方法两种类型。k-means聚类离散化方法属于一种无监督方法,该方法将距离作为相似性的测度,并把距离近的对象归为一类或一簇,其能够充分考虑每一维属性的数据特点,使每一簇中的对象高度相似,同时使不同簇中的对象高度相异。但传统的k-means聚类算法存在对初始聚类中心敏感度高的弊端,聚类结果会随预先给定的聚类数目以及初始聚类中心的不同而产生波动,影响聚类的准确性和稳定性。为克服传统k-means算法的上述缺陷,本文借鉴谢娟英等提出的聚类优化思想[9],通过定义数据对象的空间分布密度并将高密度数据样本作为初始聚类中心的方法,对基于k-means聚类的连续属性的离散化过程做出了改进。
定义1已知样本数据总体D={x1,x2,…,xn},通过计算样本相似性来衡量空间样本密度,对象xi的空间分布密度记作density(xi)。
(1)
由式(1)可知,density(xi)越小,表明空间中样本距离较近,样本数据密度较大;density(xi)越大,表明空间中样本距离越远,样本数据密度越小。
定义2对于任意数据对象x,将以x为中心,R为半径所形成的圆形区域称作数据对象x的邻域,记为δ。
δ={x|0 (2) 定义3设样本数据集X={xi|i=1,2,…,n},则类簇平均质心距离的平均值记为E: (3) 连续属性离散化的具体算法步骤如下: 步骤1利用误差平方和(SSE)指标确定初始聚类中心数目k并计算所有样本对象的密度density(xi),并定义一个初始化中心点集M={}; 步骤2选择density(xi)最小的样本对象xmin=min{xi|xi∈D,i=1,2,…,n}作为第一个初始中心点,添加到中心点集M中,即M=M∪{xmin},并从样本数据库D中删去该对象,即D=D-{xmin},根据定义2计算xmin邻域内的所有的样本对象,并从样本数据库D中删去; 步骤3重复执行步骤2,直到初始中心点集中有k个中心点作为初始聚类中心,即|M|=k; 步骤4根据欧氏距离来判断相似度量,确定每个数据对象属于哪个簇,计算并更新每个簇中对象的平均值,并将其确定为新的聚类中心; 步骤5计算类簇平均质心距离的平均值E; 步骤6循环步骤4、步骤5直到E收敛为止,得到聚类结果; 步骤7使用聚类结果中的类簇标签代替类簇中数据的值,将连续属性离散化。 近年来,粗糙集理论(Rough Set Theory, RST)[11]被广泛用于机器学习、知识获取、决策分析等领域。粗糙集方法应用于指标筛选,是根据粗糙集的属性约简原理,依赖于数据本身的性质从大量指标中剔除相关指标和冗余指标,提取核心指标,从而得到约简指标体系。 定义4对每个属性子集R⊆A,R在U上的不可分辨的二元关系IND(R)为: IND(R)={(xi,xj)∈U×U,∀r∈R,(r(xi)=r(xj))} (4) 定理1设信息表S=(U,A,V,f),R⊆A且r∈R。 如果IND(R)=IND(R-{r}),则称r在R中是冗余的,否则r在R中是必要的。 假设Q∈R,若Q独立,且IND(Q)=IND(P),则论域U在属性集P上的约简为Q,Q的所有约简组成的集合记为Red(B)。 定义5若P⊆A,X⊆U,x∈U,集合X关于I的下近似为: apr-P(X)=∪{x∈U:I(x)⊆X} (5) 集合X关于I的上近似为: (6) X的P正域为: posP(X)=apr-p(X) (7) 若指标集A和指标集A-ai生成的等价类的数量一致,那么指标ai即为冗余指标,否则,指标ai即为不可或缺的指标。 设S⊂P,S为P的Q约简,当且仅当S是P的Q独立子族且posS(Q)=posP(Q),P的Q约简称为相对约简。 在理论分析的基础上,本文采用的基于粗糙集的属性约简思路如下: (1)确定属性集。根据初选指标确定属性集,建立信息表。 (2)连续属性的离散化。利用本文提出的基于改进k-means聚类的离散化方法对连续数据指标进行离散化,构建属性约简决策表,明确条件属性和决策属性。 (3)属性约简。求取粗糙集信息系统中评价对象的等价类,由知识的相对约简原理删除影响决策属性的冗余指标。 (4)KW检验。对最终保留的指标作显著性分析,以验证指标筛选方法的效果。若KW检验中概率P值小于选定的显著性水平,则拒绝原假设,表明筛选后的指标间存在显著性差异,构建的指标体系是合理的。 图1 指标筛选过程 本文选取2016年我国31个省、自治区和直辖市的绿色经济指标数据,原始数据来源于2017年《中国统计年鉴》、《中国环境统计年鉴》、《中国城市建设统计年鉴》、《中国能源统计年鉴》、《中国教育统计年鉴》、《中国科技统计年鉴》和全国环境统计公报。 根据可获得性、可测性与可操作性原则初选指标,保证初步筛选出的指标符合实际且可量化,能够有足够的客观数据作支撑。从绿色经济的内涵及基本特征、海内外权威机构及学者的研究成果[12,13]出发遴选出28个指标,并设置经济发展、资源环境、社会民生、政策支持四个准则层,如表1所示。 表1 绿色经济评价指标集及筛选结果 指标数据的标准化,是通过数学变换将不同量纲或单位的数据无量纲化的方法。记第i个省份对应的第j个指标的标准化后值为mij(i=1,2,…,31;j=1,2,…),第i个省份对应的第j个指标的原始数据为nij(i=1,2,…,31;j=1,2,…)。对于正向指标,指标数据越大,说明绿色经济水平越高,正向指标的标准化公式为: (8) 对于负向指标,指标数据越小,说明绿色经济水平越高。负向指标的标准化公式为: (9) 式中,mij∈[0,1]。 由式(8)和式(9)及表1中注明的指标类型,得到标准化处理后的值,列入表2。 表2 标准化数据及信息表 将标准化后的数据按照1.1中的算法进行离散化处理。 利用R软件计算出最优聚类中心数目,即k=2,按照步骤2、步骤3的方法计算得到初始聚类中心,进而得到离散化结果见表2。 在将原始数据标准化和离散化的基础上,以各准则层的指标作为条件属性,以系统聚类结果作为决策属性,将28个指标按照四个准则层分别形成四个决策表,运用R软件进行编程,基于1.2中的相对约简原理删除准则层内对评价对象没有显著影响的指标。 现以经济发展准则层为例,详述该准则层指标的筛选过程,其他三个准则层的求解方法同理。经济发展准则层的决策表如表3所示。 表3 经济发展准则层的决策表 其中,U代表省份,x1~x31分别代表北京、天津等31个省,c1~c6分别代表国内生产总值、财政收入占GDP比重、失业率、第三产业比重、城镇居民人均可支配收入6个影响决策指标的条件指标,D代表各省份的聚类结果。 令C={C1,C2,C3,C4,C5,C6}为条件属性集,D={d}为决策属性集,计算过程如下: 由C导出的等价类为:U/C={{x1},{x2},{x3,x4,x5,x6,x7,x8,x12,x13,x14,x18,x22,x23,x24,x25,x27,x30},{x10,x11},{x9},{x15},{x16},{x17,x20,x21,x26,x28,x29},{x19},{x31}}。 由D导出的等价类为:U/D={{x1,x3,x9,x10,x11,x15,x16,x17,x18,x19,x23},{x2,x4,x5,x6,x7,x8,x12,x13,x14,x20,x21,x22,x24,x25,x26,x27,x28,x29,x30,x31}}。 D的C正域:posC(D)={x1,x2,x9,x10,x11,x15,x16,x19,x31},U/(C-{c1})={{x1},{x2},{x3,x4,x5,x6,x7,x8,x12,x13,x14,x18,x22,x23,x24,x25,x27,x30},{x9},{x10,x11},{x15},{x16},{x17,x20,x21,x26,x28,x29},{x19},{x31}}。 D的C-{c1}正域:pos(C-{c1})(D)={x1,x2,x9,x10,x11,x15,x16,x19,x31}。 因此,pos(C-{c2})(C)≠posD(C),c2是C中必要的,保留。同理可得:U/(C-{c2})={{x1},{x2},{x3,x4,x5,x6,x7,x8,x12,x13,x14,x18,x22,x23,x24,x25,x27,x30},{x9},{x10,x11},{x15},{x16},{x17,x20,x21,x26,x28,x29},{x19},{x31}}。 D的C-{c2}正域:pos(C-{c2})(D)={x1,x2,x9,x10,x11,x15,x16,x19},因此,pos(C-{c2})(C)≠posD(C),c2是C中必要的,保留。同理可得:pos(C-{c3})(C)=pos(C-{c6})(C)=posD(C),pos(C-{c4})(C)≠pos(C-{c5})(C)≠posD(C)。 所以c1、c3、c6是C中D不必要的,约简删除,c2、c4、c5是C中D必要的,保留。经过相对约简删除后,经济发展准则层剩余指标为财政收入占GDP比重、第三产业比重、城镇居民人均可支配收入3个指标。 同理对资源环境、社会民生、政策支持三个准则层执行指标筛选过程,共删除13个指标,保留突发环境事件次数、工业用水量、电力消费量等9个指标。 经过相对约简删除后,从28个海选指标中保留12个指标,最终筛选结果见表1。 通过基于粗糙集相对约简原理的指标筛选,在初选的28个指标中保留了12个指标,且在显著性水平为0.05时,KW检验的检验概率值为0.007,说明构建的绿色经济指标体系中各指标间具有显著差异,从而验证了指标筛选模型的合理性。 本文针对k-means聚类结果对初始聚类中心具有敏感性的问题,定义了样本空间分布密度,从而改进了k-means聚类离散化方法。在此基础上,基于粗糙集知识的相对约简原理,确定了指标体系的约简,剔除包含重复信息的冗余指标。以绿色经济评价指标体系的构建为实证对象,将初选的28个指标约简为12个指标,验证了基于k-means与粗糙集相对约简原理的指标筛选模型的可行性。通过KW检验证明最终筛选的指标具有显著性差异,说明了指标筛选模型的合理性。
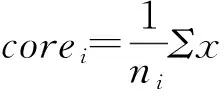
1.2 粗糙集属性约简理论

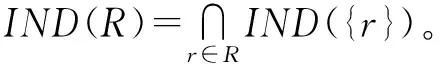
1.3 基于粗糙集的属性约简模型
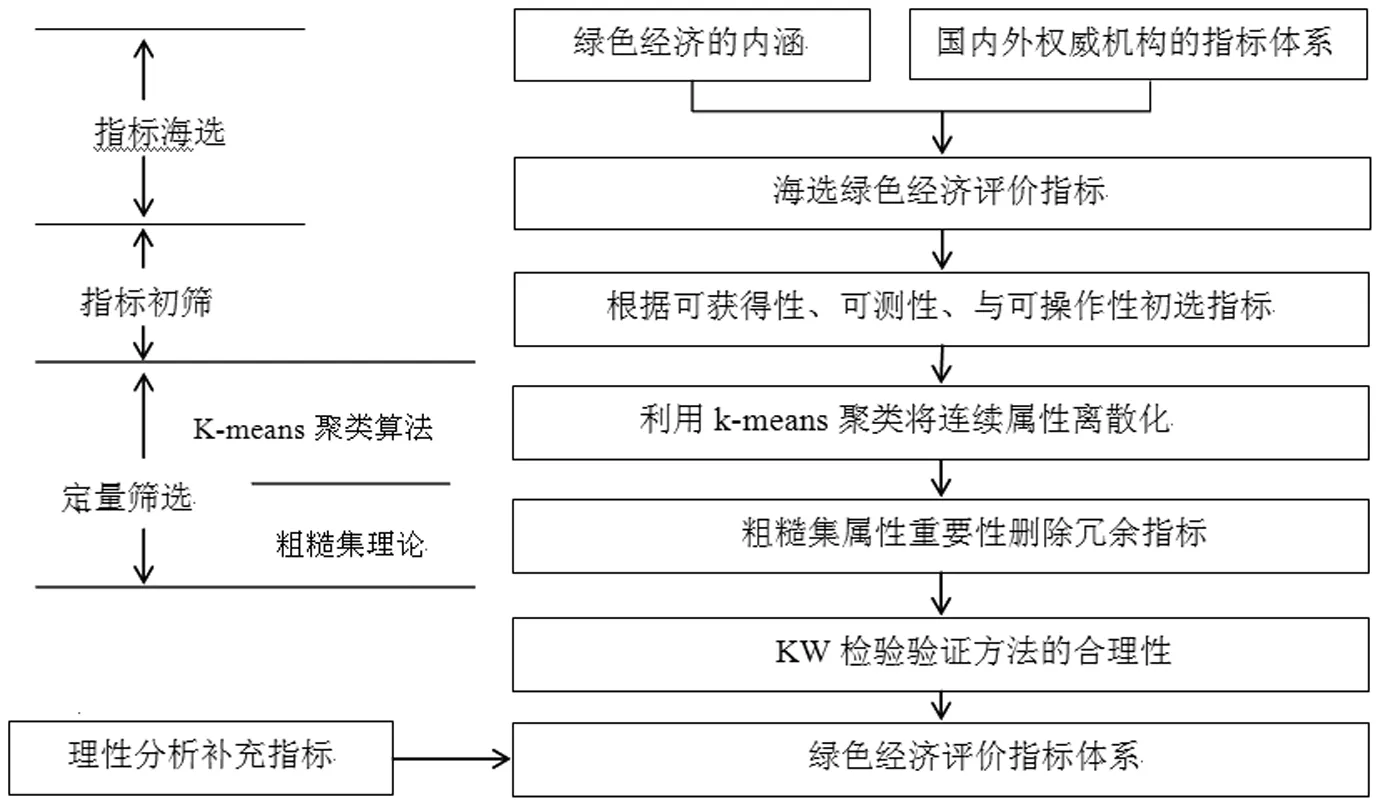
2 实证分析
2.1 样本选取及数据来源
2.2 评价指标的初选

2.3 指标数据的标准化

2.4 基于改进k-means聚类的数据离散化
2.5 基于决策表相对约简原理的指标筛选

2.6 指标筛选合理性分析
3 结论
