考虑合乘的降级路网道路收费研究
2021-01-07张凌煊
丁 冬,帅 斌,张凌煊
(1.重庆邮电大学 经济管理学院,重庆 400065;2.西南交通大学 交通运输与物流学院,四川 成都 610031)
0 引言
交通拥堵已经成为世界性的难题。目前已有许多措施来治理交通拥堵,如拥挤收费、信号灯配时、限行或限购等。但每种方法都有相应的不足之处,如拥挤收费难以让公众接受,信号灯配时在大规模城市网络中难以实现等。相对而言,合乘出行方式可减少交通量而很少抑制交通需求,是缓解拥堵的一种较好的方法。但出行者通常出于隐私等各方面因素的考虑,通常不愿意选择合乘出行。这就需要一定的措施来促进出行者合乘,例如HOV/HOT车道,网络合乘平台服务等。但这些方案的效果也不明显。
现有研究表明,道路收费对出行者的出行模式选择有明显的影响。据此猜测,道路收费是否可以作为一种促进合乘的手段。在许多城市道路中并没有HOV车道,因此有必要分析在普通城市道路中道路收费对合乘的促进效果。由于合乘减少了交通量,对环境的影响因素也应予以考虑。同时,出行时间、出行费用与出行时间可靠性是出行者考虑的主要因素,而降级路网是产生时间可靠性的重要原因。因此,本文考虑在降级路网中研究道路收费对合乘的作用,并考虑排放的影响。道路收费的相关理论已有大量的研究。Yang和Huang出版了专著,对道路收费的原理、在交通系统中的作用、道路收费的效率边界以及最优道路收费等多类问题作了理论上系统的研究,提供了多种理论与方法。Wu等研究了多模式网络中基于帕累托改进的拥挤收费,提出了相关模型与算法;在道路排放方面,有关于排放收费、排放许可、以排放为基础的交通分配等研究。Nagurney和Ramanujam以在道路上设置排放许可,建立了符合出行者用户均衡的模型,并提供了相应的算法;Yang等建立了区域排放收费的多目标模型,并设计了算法;Yin和Lawphonepanich提出了计算路段排放量的模型,并将其应用于路网均衡的模型中,探索了加入路段收费的效果;杨文国和高自友建立了考虑路段一氧化碳约束的交通流分配模型,并提出了基于惩罚函数的求解算法。降级路网的研究通常与可靠性联系在一起。在可靠性方面,Lo等提出了降级路网行程时间可靠性,并将可靠性量化,用于交通均衡的计算中;Chen等计算了整个路网的通行能力可靠性;同时,Chen等提出了评价通行能力可靠性的方法;Yan等研究了降级路网中如何设置道路限速达到总出行费用最小的问题。
综上,在降级路网中道路收费对合乘的影响目前尚无分析。鉴于降级路网在现实当中广泛存在,本文在降级路网中探索道路收费对具有合乘的交通系统的影响,以社会福利最大化及排放最小为目标,有助于促进合乘,提高交通系统性能。
1 符号定义
考虑交通网络G(N,A),N为节点集合;A为路段集合;W为OD对集合;L为网络中路径的集合;路段a的容量为Ca,最大容量为,降级系数为θa。网络中出行方式集合为M。路网中存在两种出行方式:单独驾驶与合乘,m =1为单独驾驶,m=2为合乘,本文中以2人合乘为例。为OD对w间路径l上以m方式出行的流量;为OD对w间m出行方式的需求为路段a上以m方式出行的流量为路段a上的车流量。
2 降级路网的出行时间期望与方差
本文采用BPR函数表达路段旅行时间,如下所示:

式中,ta为路段出行时间为路段自由流出行时间;β,n为参数。
根据文献[7],降级路网中路段出行时间的期望为:
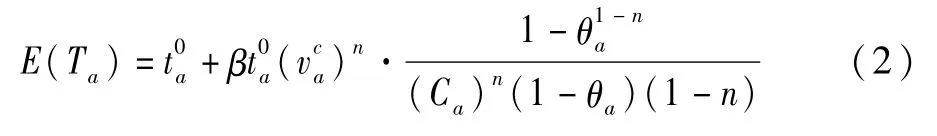
路段出行时间方差为:
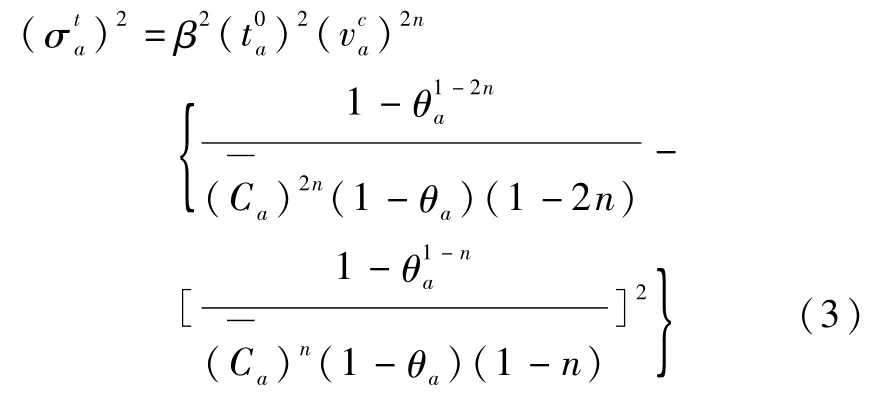
3 出行时间费用
出行者除了考虑出行时间外,还需要考虑时间不确定性,而在合乘情况下还具有合乘成本。因此,单独驾驶出行者与合乘出行者的路径出行函数可用下式表示:

4 交通方式划分
本文采用Logit模型划分单独驾驶与合乘的交通模式,可用下式表达
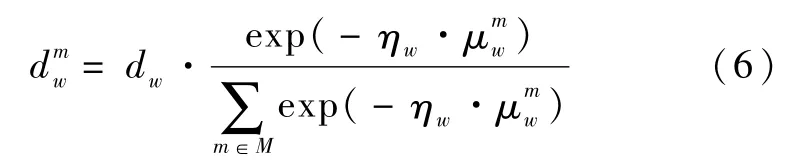
5 路网均衡
本文采用变分不等式表述路网均衡,以wardrop第一原理为准则,当路网达到均衡状态时,出行者选择费用相等且最小的路径。
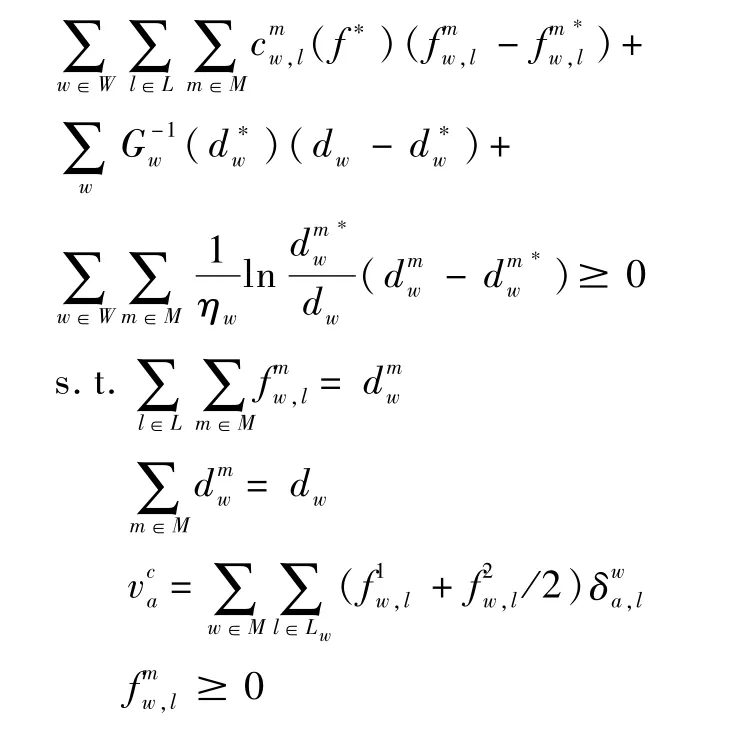
6 社会福利与排放
社会福利即交通路网中的消费者盈余,是在交通研究中衡量路网表现的重要指标,从经济学中发展而来。Williams和Evans从经济的角度在弹性需求的情况下采用社会福利衡量了路网优劣,社会福利成为交通中弹性需求下衡量路网优劣的重要指标。很多文献都将社会福利作为指标,采用拥挤收费、限行、限速等交通管理方案对路网进行优化。社会福利为消费者的总效用减去总成本,即为图1中阴影部分总和减去斜线阴影部分。

图1 社会福利
在交通系统中,X表示出行者需求,P为出行者费用,X0,P0分别为均衡状态下的出行需求和费用。当总效用超过极大值时,出行者边际效用为0,不会再有出行者出行。因此,社会福利表示了路网中出行者的出行意愿得到满足的情况。从图中可以计算社会福利:

同时,应考虑交通系统的排放。排放的计算公式为[5]:
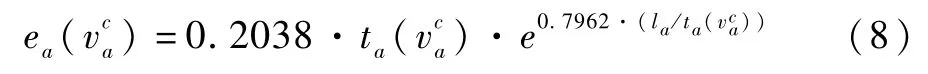
根据Lo等对可靠性期望的描述,路段a上交通排放的期望可表示为:
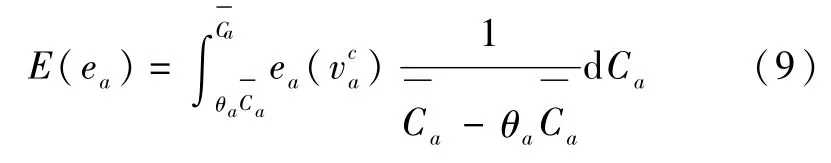
本文以一个路网为例,检查道路收费对两个指标的作用。
如图2所示,一共11条路段,4个OD对。具体参数如表1所示。OD对w间的出行需求dw表示为:

其中,最小广义费为:
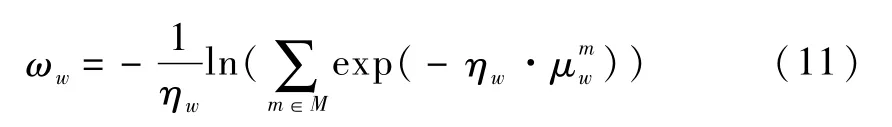
其余参数为:λt=2;Δ=6;κ=0.05;η1=0.1;η2=0.2;η3=0.3;η4=0.2;β=0.15;n=4;θa=0.6。史峰和李志纯使用此虚拟路网验证了网络扩容和拥挤收费的组合模型以及求解算法,说明了路网的合理性,其路段自由旅行时间、通行能力、OD需求以及路网各项参数等均符合实际情况。
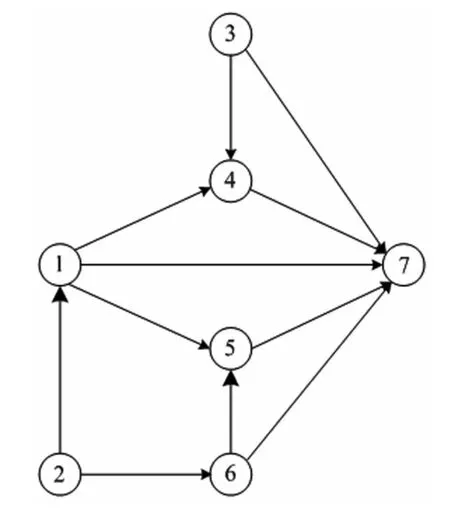
图2 算例网络

表1 路段属性
当在路段(1,7)上实施从1到10的收费时,社会福利及排放的变化趋势如图3所示:
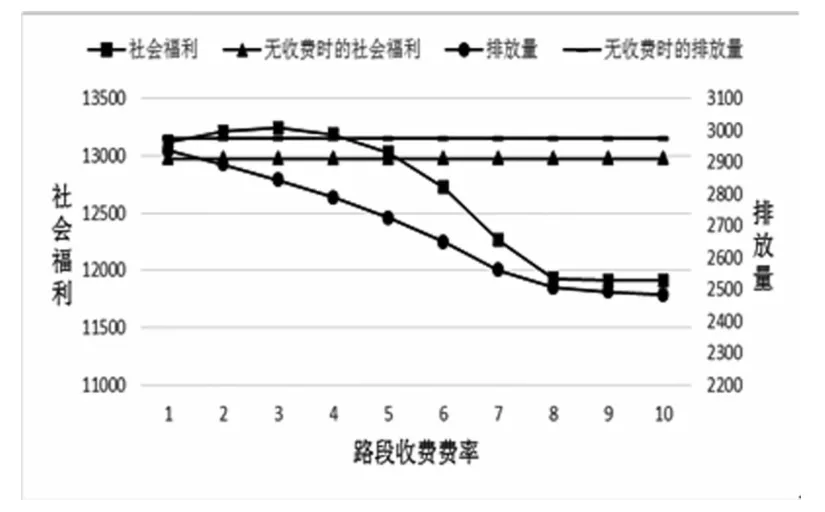
图3 不同费率下社会福利与排放量
由图中可以看出,社会福利先升后降,在两个路段费率为5时约等于不收费时的社会福利,这是因为收费调节了出行方式选择与路段流量的结果;而排放量一直下降,说明更大的费率促使更多的人选择合乘,交通量减少。但费率过大时,出行费用过大,社会福利也会下降。图中可以看出,社会福利与排放量的变化并不一致,因此优化交通系统需要同时考虑两个目标。
7 路段最优收费
为了获得路段最优收费费率,可采用双层规划。上层双目标函数为双目标规划,下层目标函数为5中变分不等式。因此,上层目标函数可以表示为:
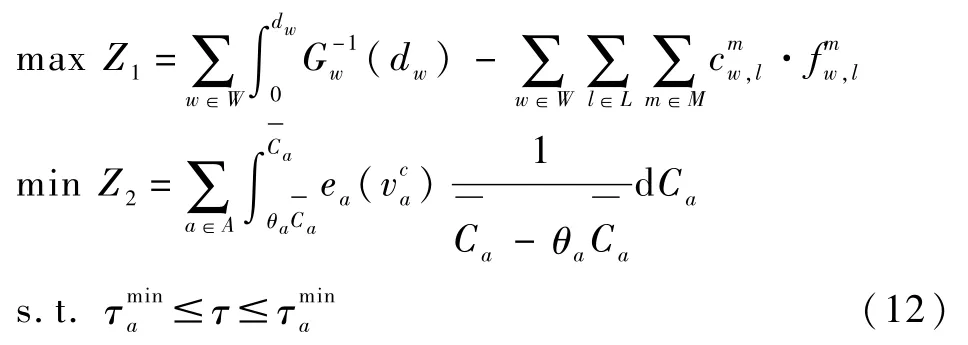
约束条件为路段收费不能超过预先设定的值,以确保结果符合实际情况。
由于下层模型的复杂性以及双层规划的特性,算法应具有高效可行的性质。Yang等采用了NSGA II求解多目标的双层规划模型,可以快速有效地求解多目标优化问题。本文也采用此算法。具体算法步骤如下:
(1)初始化。随机产生初始父代种群P0,其大小为N,进入步骤2。
(2)对P0进行选择、交叉、变异产生下一代种群q0,将P0与q0合并,产生种群Pt,其大小为2N,进入步骤3。
(3)将Pt按非支配关系排序。对Pt中每一个体i设置ni和Si两个参数,ni为种群中支配个体i的解的数量,Si为被个体支配的解的集合。找出种群中ni=0的个体,存入集合F1,考察F1中每一个个体所j支配的个体集合Sj,将Sj中每个个体j的nj减去1。如果nj-1=0则将此个体j存入集合F2。给F1中的元素赋予非支配序irank,然后对F2中的元素进行上述分级操作并赋予非支配序,直到所有的个体都被分级并且被赋予非支配序为止,进入步骤4。
(4)将F1填充入新的种群中。如果元素数量小于N,则继续添加F2,以此类推,直到元素数量大于N或等于为止。若元素数量等于N,得到新种群Qt,进入步骤6,若元素数量大于N,进入步骤5。
(5)将最后一个填充入新种群的集合Fn取出,设此时新种群中的元素个数为n。对Fn中的元素进行拥挤度排序。具体步骤为:设Fn中有l个元素,每一个元素的初始拥挤度I(i)d=0。同时,置I(1)d=I(l)d=∞。对于从第2到l-1个元素,有I(i)d=I(i)d+[I(i+1)m-I(i-1)m]/,其中,I(i+1)m为第i个个体对应的第m个目标函数的值。针对每一个个体,都可计算一个拥挤度id。取拥挤度id更大的前N-n个个体填充入新种群中,形成新种群Qt,进入步骤6。
(6)按照遗传算法进行选择、交叉、变异,得到子代新种群qt。将Qt与qt合并,得到新种群Pt,进入步骤7。
(7)若已满足预先设置的迭代次数,输出最后的解;若尚未达到设置的迭代次数,返回步骤3。
其中,染色体维度等于路段收费费率经过编码转换后的集合的元素数量。NSGA II算法与基本遗传算法的区别在于,经过了快速支配排序与拥挤度确定,将种群中的染色体在选择交叉变异之前进行了分级,每一次都可以取得最优的染色体,加快了优化速度与精度。
8 算例设计
算例即为图2中所示算例。费率上下限设置为(2,10)。参数如表1所示。一共产生10个非支配解s1~s10,如表2所示。s0表示无道路收费的情况。
10种方案对于社会福利与总排放量均有改善。由于施加了收费,将外部成本内部化,社会福利提高了10%左右;由于增加了出行费用,需求减少23%左右,车辆数相应减少,因此排放下降,大约下降35%左右。但10种方案的差别并不大,这或许是由于问题本身的特性造成。其中,方案s3,s8,s10更侧重于排放,而其他方案更侧重于社会福利。同时,路段时间总方差也减少,说明道路收费有减少出行时间不确定性的作用。图4列出了s1的路段收费费率。
图5描述了多个非支配解组成的优化解边界。由图中可以看出,非支配解能够优化两个目标函数。非支配解社会福利大于未收费时的社会福利,最高约为14350,能提升大约10%,而排放量也会小于未收费时的排放量,最低约为1700,大约能降低40%。这是因为在具有合乘模式的系统中,收费虽调节了流量,但相对来说交通需求下降更为明显,因此对排放的作用更大。在非支配解中,排放量的变化不大,这或许是由于问题本身的特性造成。但也说明在实际应用中,如对排放没有特别严格的要求,更应选择社会福利较大的方案,因为排放量变化并不大。

表2 非支配解下的社会福利、排放量、需求与方差

图4 方案费率
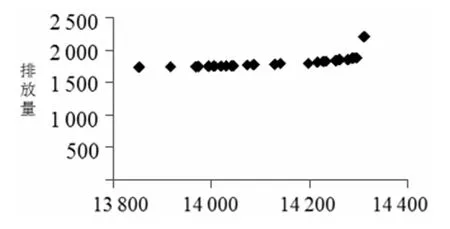
图5 非支配解边界
9 结论与展望
本文模型考虑了社会福利和排放两个目标函数,在具有合乘与降级路网带来的不确定的时间可靠性的条件下,采取双层规划描述了施加道路收费的具有合乘模式的交通系统,采用NSGA II算法进行了求解。结果表明,道路收费可提高社会福利,降低排放与路网时间不确定性。同时描绘了最优解的边界,说明同时考虑社会福利与排放时,道路收费能提升约10%的社会福利与降低40%的排放。现实中可根据边界条件判断是否需要实施道路收费。
由于时间可靠性是由需求和供给两方面引起的,本文仅仅考虑了供给方面带来的不确定性,需求方面带来的不确定性应当在未来的研究中予以考虑。同时,本文假设出行者在路径中均合乘,更符合实际情况的中途合乘的情况也应当被关注。
