基本广义随机数据包络分析方法

2021-01-07马生昀马占新乔剑敏

运筹与管理 2020年11期

马生昀，马占新，张军，乔剑敏

（1.内蒙古农业大学理学院，内蒙古呼和浩特 010018；2.内蒙古大学经济管理学院，内蒙古呼和浩特 010021）

0 引言

数据包络分析（Data Envelopment Analysis，DEA）是一种用于绩效评价的数据驱动工具［1～4］。依据评价参考系的不同将DEA方法可以分为传统DEA方法［1～3］、超效率DEA方法［5］和广义DEA方法［6］。评价某个决策单元的相对效率时，传统DEA方法的参考系为决策单元集，超效率DEA方法的参考系为决策单元集中剔除被评价决策单元，广义DEA方法的参考系为任意给出的参考系（称为样本单元集）。同时，超效率DEA方法评价不同决策单元的参考系不同，广义DEA方法评价不同决策单元的参考系相同。传统DEA方法相当于决策单元集作为样本单元的广义DEA方法。

C2R模型［1］和BC2模型［7］是最基本的传统DEA模型，基于C2R模型和BC2模型的广义DEA模型是最基本的广义DEA模型［8，9］。经过多年的发展，传统和广义DEA方法的理论和应用研究都取得了丰硕的成果［10，11］。其中带有随机因素的传统DEA方法也有了一定的研究［12～16］，文［17］初步研究了样本单元为随机变量，决策单元确定的基于C2R和BC2模型的基本广义随机DEA方法。

本文继续讨论决策单元和样本单元均为随机变量的基本广义DEA方法。在第1节和第2节中，分别基于期望值模型和机会约束规划把含有随机样本单元和随机决策单元的广义DEA有效性评价模型转化成确定性模型进行求解。一般情况下，利用统计学方法可能无法得到随机样本单元和随机决策单元的输入输出指标服从的具体分布；或者即使得到了每个输入输出指标的具体分布，但是评价模型中相应指标加权和服从的分布无法获得。相对来说，利用统计学方法容易获得各输入输出指标数学期望的估计值，所以在实际问题中基于期望值模型对随机决策单元相对于随机样本单元进行广义DEA有效性评价更容易实现。如果能够得到每个输入输出指标的具体分布并计算获得相应指标加权和服从的分布，那么可以利用机会约束规划对决策单元进行广义随机DEA有效性评价，能够体现随机变量取值的波动情况（方差）对有效性的影响。一般情况下，加权和分布不易获得，本文对此只做了初步讨论，考虑了样本单元和决策单元的输入指标间相互独立，输出指标间相互独立并且服从正态分布的特例。由于输入输出指标是随机的，在可以求得加权和分布的前提下基于机会约束规划的评价方法更加全面。基于两种不同的方法进行确定性转化，主要区别在于能否体现方差的影响，进而分别获得的评价结果可能存在差异。

1 基于期望值模型的基本广义随机DEA方法

假设有n个决策单元（Decision Making Unit，DMU）和个样本单元（Sample Unit，SU）。DMUP和SUj的输入输出向量分别为

各分量均为随机变量。数学期望分别为

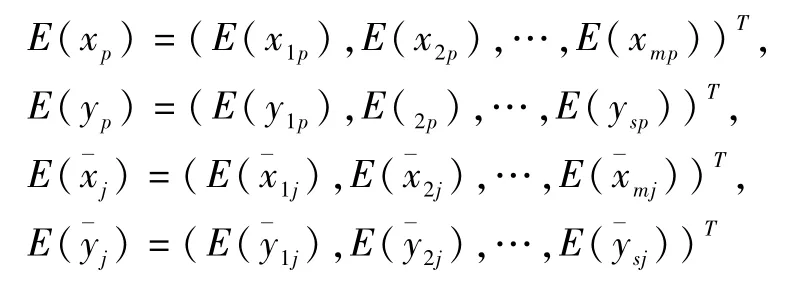
称TDMU＝｛（x1，y1），（x2，y2），…，（xn，yn）｝为决策单元集。

记T（1）＝T，ET（1）＝ET，称T为样本生产可能集，ET为期望样本生产可能集。

相对于ET（d）评价决策单元（xp，yp）的基于期望值模型的基本广义随机DEA模型（M1″）如下。

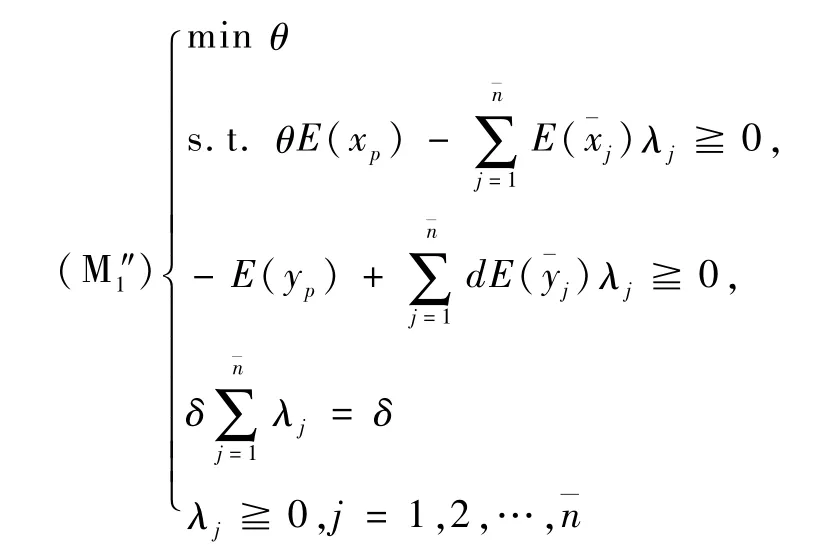
其中δ＝0或1，d称为移动因子，d＞0。

定义1如果不存在（x，y）∈ET（d），使得E（xp）≧x，E（yp）≦y，并且E（xp）≠x或E（yp）≠y，则称决策单元（xp，yp）相对于期望样本前沿面的d移动有效或广义期望DEAd有效，简称GEDEAd有效。反之，称决策单元（xp，yp）为GEDEAd无效。

当d＝1时，GEDEA1有效可以记为GEDEA有效，即（xp，yp）相对于期望样本前沿面有效。

其中δ＝0或1，d称为移动因子，d＞0。

定义2若模型的任意最优解j＝0，1，2，…都有θ0＝1，并且则称决策单元（xp，yp）为GEDEAd有效。反之，称决策单元（xp，yp）为GEDEAd无效。

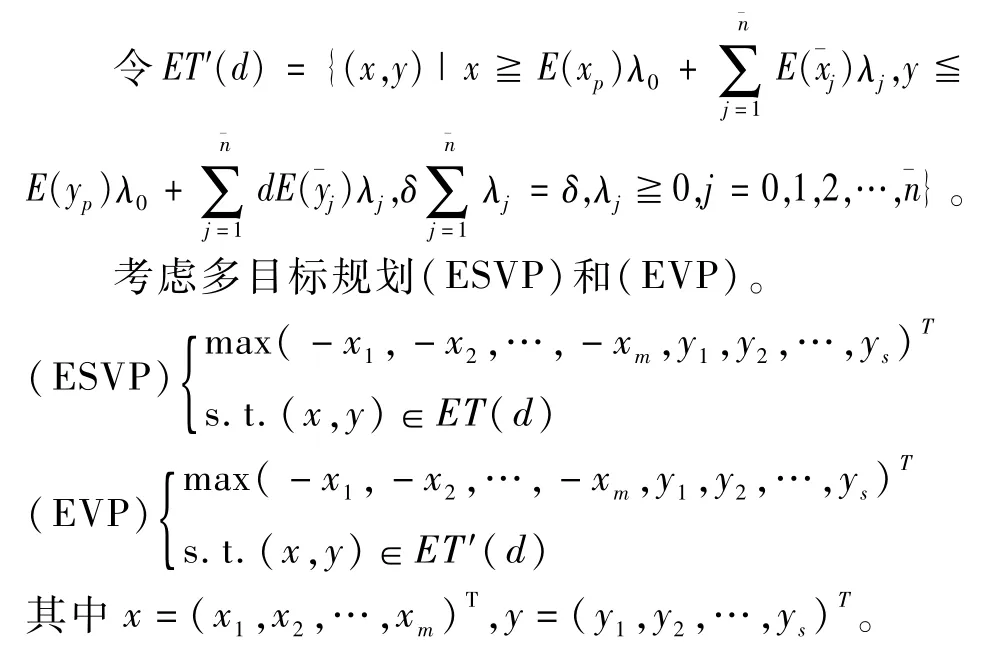
由文献［17］中的引理2.3和引理2.4类似可得定理1和定理2。

定理1决策单元（xp，yp）为GEDEAd有效当且仅当（E（xp），E（yp））∉ET（d）或（E（xp），E（yp））为多目标规划（ESVP）的Pareto有效解。

定理2决策单元（xp，yp）为GEDEAd有效当（E（xp），E（yp））且仅当为多目标规划（EVP）的Pareto有效解。

步1给定步长d+＞0。令k＝1。

步2应用（）计算DMUa和DMUb的有效性。若DMUa和DMUb中一个为如下。

步3若DMUa和DMUb均为有效，执行步4；若二者均为无效，执行步5。

步4令k＝k+1，执行步2。

步5给定步长d+＝d+-d0＞0，其中d0＞0，执行步2。

步6若DMUa为有效，DMUb为无效，则DMUa≻DMUb；反之，DMUb≻DMUa。停止。

2 基于机会约束规划的基本广义随机DEA方法

利用机会约束规划进行评价可以体现方差（离散程度）对于DEA有效性的影响。假设模型中含随机因素的约束条件满足置信水平1-α，评价决策单元（xp，yp）的基于机会约束规划的基本广义随机DEA模型（）如下。

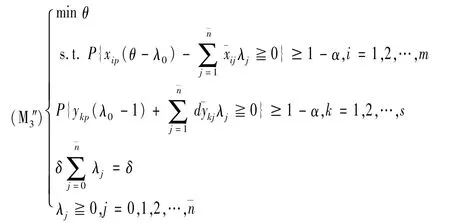
其中δ＝0或1，d称为移动因子，d＞0，0≦α≦1。

定理3若θ*为模型的最优值，则θ*＝minθ≦1。

证明显然是模型的可行解，所以minθ≦θ0＝1。

令Xi（α），Yk（α）分别表示Xi，Yk的上α分位点，即P｛Xi≧Xi（α）｝＝α，P｛Yk≧Yk（α）｝＝α，i＝1，2，…，m，k＝1，2，…，s。

定义3如果模型的任意最优解＝0，1，2，…，都有i＝1，2，…，m，k＝1，2，…，s，则称决策单元（xp，yp）相对于机会约束样本前沿面的d移动为1-α有效或广义机会约束DEAd有效，记作1-αGCDEAd有效。否则，称决策单元（xp，yp）为1-αGCDEAd无效。

考虑一种特殊情形，假设两种单元的输入之间独立，两种单元的输出之间独立，并且所有输入输出指标均服从正态分布。假设，其中i＝1，2，…，m，k＝1，2，…，s，p＝1，2，…，n，j＝1，2，…

对任意i＝1，2，…，m，因为xip（θ-λ0）-，所以1-α等价于

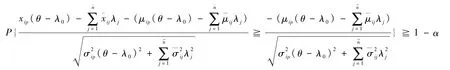
当两种单元的输入之间独立，两种单元的输出之间独立，并且所有输入输出指标均服从正态分布，模型等价于模型

当两种单元的输入之间独立，两种单元的输出之间独立，并且所有输入输出指标均服从正态分布时，与评价决策单元广义期望DEA有效性类似，可以通过（M5″）利用调整移动因子d，相对于样本单元对各决策单元的广义机会约束DEA有效性进行排序。

3 算例

假设有5个样本单元和4个决策单元，均为双输入双输出，两种单元的输入之间独立，两种单元的输出之间独立，具体指标数据在表1和表2中给出。

表1 样本单元输入输出指标的分布

表2 决策单元输入输出指标的分布

表3 GEDEA有效性与GCDEA有效性

由表3可知，DMU2为GEDEA1无效，DMU1，DMU3，DMU4均为GEDE A1有效。GEDEA1有效决策单元可以依据期望样本前沿面的d移动进一步区分。令步长d+＝0.1。当d′＝1.1时，DMU1和DMU3均为GEDEA1.1有效，DMU4为GEDEA1.1无效。当＝1.2时，DMU1和DMU3均为GEDEA1.2有效。当＝1.3时，DMU1为GEDEA1.3有效，DMU3为GEDEA1.3无效。综上，4个决策单元的GEDEA有效性排序为DMU1≻DMU3≻DMU4≻DMU2。

从表3同样可知，DMU1和DMU3为0.95GCD EA1有效，DMU2与DMU4为0.95GCDEA1无效。基于机会约束样本前沿面的d移动可以对决策单元的有效性进一步区分。令步长d+＝0.1。对0.95GCDEA1有效决策单元，当d′＝1.1时，DMU1为0.95GCDEA1.1无效，DMU3为0.95GCDEA1.1有效。所以二者的有效性排序为DMU3≻DMU1。对0.95GCDEA1无效决策单元，当d1＝1-d+＝0.9时，DMU4为0.95GCDEA0.9有效，DMU2为0.95 GCDEA0.9无效，所以二者的有效性排序为DMU4≻DMU2。综上，4个决策单元的GCDEA有效性排序为DMU3≻DMU1≻DMU4≻DMU2。

通过算例看到，基于期望值模型和机会约束规划对广义随机DEA有效性进行确定性转化得到的评价结果可能不尽相同。对单个决策单元进行评价，比如DMU4为GEDEA1有效，但非0.95GCDEA1有效。从4个决策单元利用移动因子排序看，DMU1和DMU3的两种广义随机DEA有效性排序结果不同。这说明样本单元和决策单元的输入输出指标的随机性会对决策单元的有效性产生影响，基于期望值模型不能体现方差的影响，基于机会约束规划可以体现方差的影响。