天然食用色素的多元线性模型和神经网络模型的配色效果比较
2021-01-07朱大洲刘国荣王成涛
刘 亚,雷 声,朱大洲,高 莉,刘国荣,王成涛,*,刘 娟,郭 青
(1.云南中烟工业有限责任公司 技术中心, 昆明 650202;2.北京工商大学 北京市食品添加剂工程技术研究中心, 北京 100048;3.农业农村部食物与营养发展研究所, 北京 100081)
食品着色剂(食用色素)是食品添加剂的重要门类,广泛应用于食品、医药、化妆品、印染、烟草等工业领域[1-2]。在食品及包装中应用食用色素,可赋予其鲜艳的颜色,吸引消费者,刺激其视觉、听觉、嗅觉与味觉,在生理和心理方面影响消费行为[3-7]。近年来,发现多种天然食用色素还具有一定生理活性、保健功能,可作为食品营养强化剂[8-9]。
食用色素呈现出不同的颜色,是其对不同波长的光选择性吸收的结果。光谱曲线则是以物质的吸光度为依据,反映物质颜色特性的曲线。通常色素的光谱曲线也被称为色素颜色的“指纹”[3,10]。目前,天然食用色素的调配仍大多依靠人工配色,其高度依赖配色者的配色经验,受其心理因素、生理因素和其他条件的影响,生产效率低,产品质量稳定性差[11-12]。除人工配色外,计算机配色技术已有一些报道。近年来,基于光谱反射率重建模型建立RGB颜色空间到L*、a*、b*颜色空间的映射方法,用于颜色测量,并通过多元线性回归模型、神经网络模型等进行色素调配、织物染色的研究已见报道[13-16]。相关研究表明,采用光谱曲线对天然食用色素建立配色模型,可有效提高配色模型的精确度,减少预测颜色与目标颜色之间的色差[17]。
本文基于天然食用色素的质量浓度与其在特征最大吸收波长下吸光度呈正比关系的原理,利用光谱曲线对颜色描述的唯一性特性[17-18],构建了天然食用色素的2种配色模型。通过分析预测多元线性模型和神经网络模型对天然食用色素的复配效果,以及对比2种模型的预测性能,选出较优模型,并完成了对较优模型的复配验证。希望研究结果可以为天然食用色素的配色模型构建、智能配色等提供新的理论依据和技术参数。
1 材料与方法
1.1 材料与仪器
红曲红、栀子黄、栀子蓝色素,河南中大恒源生物科技股份有限公司。
UV- 3600 Plus型紫外- 可见分光光度计,岛津仪器有限公司;CM- 3610A型色差仪,日本柯尼卡美年达公司;BSG- 300型光照培养箱,上海博讯实业有限公司医疗设备厂。
1.2 实验样品配制
选择红曲红、栀子黄和栀子蓝三原色色素按照一定比例进行复配,得到复配色素溶液,共计156组样品,其制备配比见表1,其中样品1-31为单一色素溶液,样品32-156为复配色素溶液。
1.3 样品色素溶液的特征吸收光谱及颜色参数分析
1.3.1色素溶液的特征吸收光谱分析
紫外- 可见分光光度计于350~720 nm波长内,测定表1样品溶液的可见光吸收光谱,每样品测量3次,取其平均值进行训练和优化模型[18]。
1.3.2单色及复配色素溶液的颜色参数测定
选用孔径9 mm、100% UV、D65光源、10°视角时,全自动色差仪检测表1中156组样品溶液的亮度CIEL*(L*)、红值(a*)和黄值(b*),以超纯水为空白,每个样品检测3次,取其平均值[17-18]。
1.4 数学模型的选择
1.4.1多元线性回归模型
多元线性回归模型[14]可用于描述因变量y与多个自变量x1,x2,……xn之间的线性相关关系,模型见式(1)。
(1)
式(1)中,x1,x2,…,xk(k≥2)为回归因子;y为观测值;b0,b1,b2,…,bk为回归系数;ε~N(0,σ2)为随机误差。
1.4.2神经网络模型
神经网络在近红外光谱分析中得到广泛应用,其主要由信号的正向传播和误差的反向传播组成[15-16]。正向传播时,光谱数据从输入层传入,经隐含层处理后传向输出层,若实际输出与期望输出的误差较大,此时将误差反向传播,以修改各个神经单元的权值和阈值,直到网络的输出误差减小到规定范围,或达到设定的学习次数为止。
1.5 色价计算
在GB/T 5525—2008[19]中2.2节重铬酸钾溶液比色法基础上修改。准确称取0.1 g试样,于100 mL容量瓶中用适当溶剂稀释,用溶剂作参比液于1 cm比色皿中,并用紫外可见分光光度计于最大波长处测定其吸光度,然后计算单一色素的色价,见式 (2)。
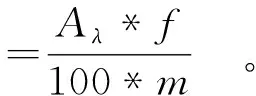
(2)
式(2)中,Aλ为实测试样在样品的最大吸收波长λ下的吸光度;f为稀释倍数;m为试样质量。
1.6 色差计算
根据CIELAB色差公式,计算色素溶液的色差,见式(3)。
(3)
式(3)中,ΔL*是指实际配方和预测配方溶液亮度的差值;Δa*是指实际配方和预测配方溶液红值的差值;Δb*是指实际配方和预测配方溶液黄值的差值。
1.7 模型精确度的评价
为更加直观评价预测模型的精确度,采用平均绝对误差(MAE)、平均相对误差(MAPE)、均方误差(MSE)和均方根误差(RMSE)等4项指标,对模型的性能进行评估,见式(4)~式(7)。
(4)
(5)
(6)
(7)
式(4)~式(7)中,Yi表示实际值;Y′表示模型预测值;i=1, 2, 3,……n;n为数据量个数。
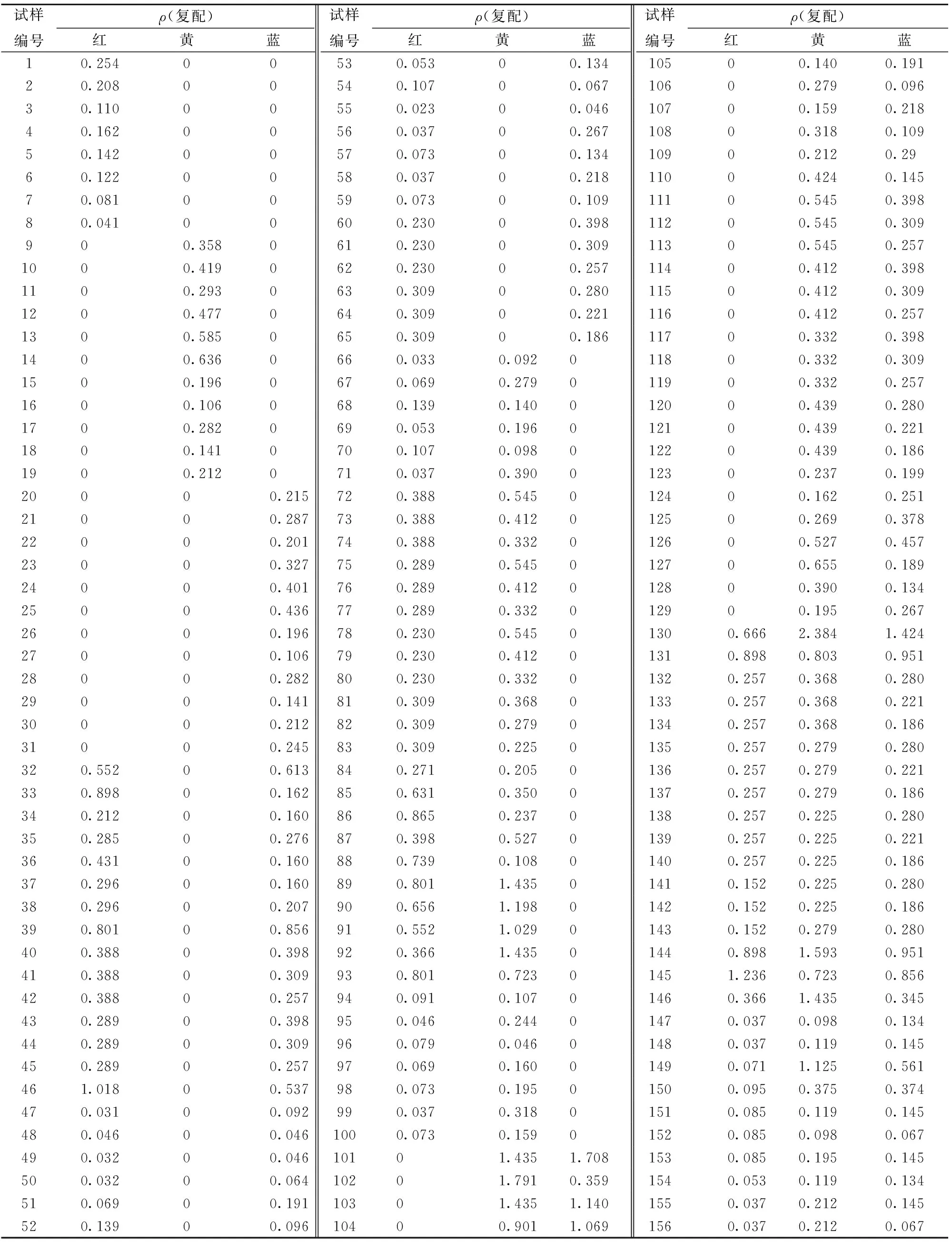
表1 不同质量浓度三原色色素的样品制备配比Tab.1 Sample preparation proportion of trichromatic pigments with different concentration g·L-1
2 结果与讨论
2.1 3种三原色色素的吸收光谱分析
于350~720 nm波长内绘制分析红曲红、栀子黄和栀子蓝色素的吸收光谱曲线(见图1),确认单一色素的最大特征吸收峰,发现其最大特征吸收波长分别为442、485、596 nm。根据单一色素溶液样品1-31的光谱曲线数据,采用式(2)计算得到红曲红、栀子黄和栀子蓝色素的色价分别为95.33、20.90和30.13。
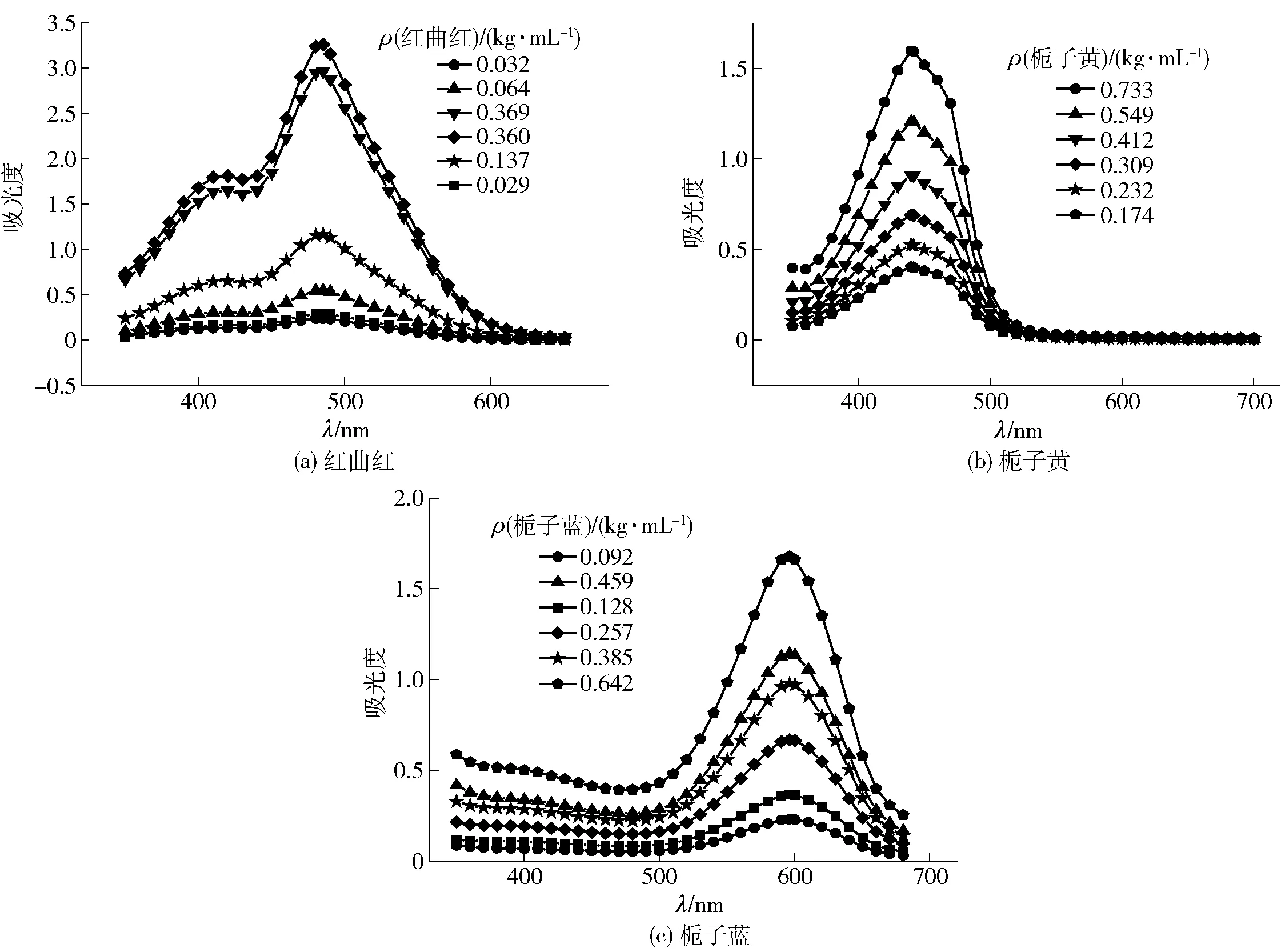
图1 不同质量浓度红曲红、栀子黄、栀子蓝色素的吸收光谱Fig.1 Absorption spectral analysis of different concentrations of monascus red pigment, gardenia yellow pigment and gardenia blue pigment
由图1可知,红曲红、栀子黄和栀子蓝色素样品溶液的吸光度与其质量浓度呈正比,随着色素质量浓度的增加,样品的吸光度也随之增加。因此,可通过色素质量浓度与色价相乘得积,计算得到3种单一色素的吸光浓度,用于构建预测模型。
2.2 3种色素复配溶液的吸收光谱分析
按照不同质量比,对红曲红、栀子黄和栀子蓝3种色素进行复配,于350~720 nm测定复配色素溶液的吸收光谱,并绘制其吸收光谱曲线(见图2),发现复配色素溶液分别于442、485、596 nm呈现特征吸收峰,与单一色素的最大特征吸收峰基本一致,且3个特征吸收峰下的色素质量浓度与其吸光度呈正相关性。此结果进一步验证了光谱曲线对颜色描述的唯一性[12,17]。
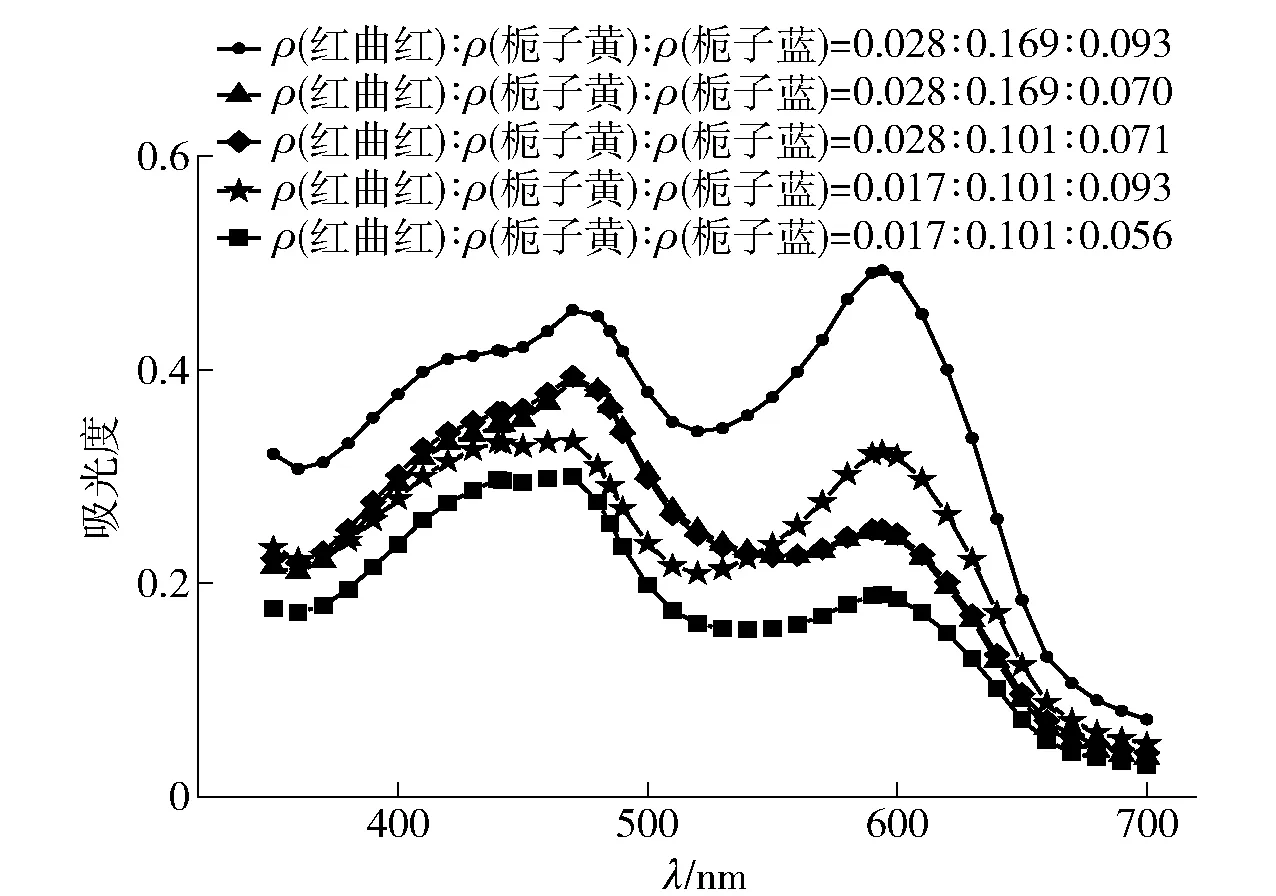
图2 不同质量浓度三原色色素复配溶液的吸收光谱Fig.2 Absorption spectral analysis of different compound concentrations of trichromatic pigments
2.3 预测模型的构建
根据图1(单一色素)和图2(复配色素)的吸收光谱,为适应色素复配的不同色价需求,扩大预测复配模型的适应性,以混合色素溶液在3个特征吸收波长的吸光度为自变量,混合色素溶液内单一色素溶液的色价质量浓度为因变量,构建多元线性和神经网络预测模型,并分析比较2个预测模型的适应性。
2.3.1多元线性预测模型构建
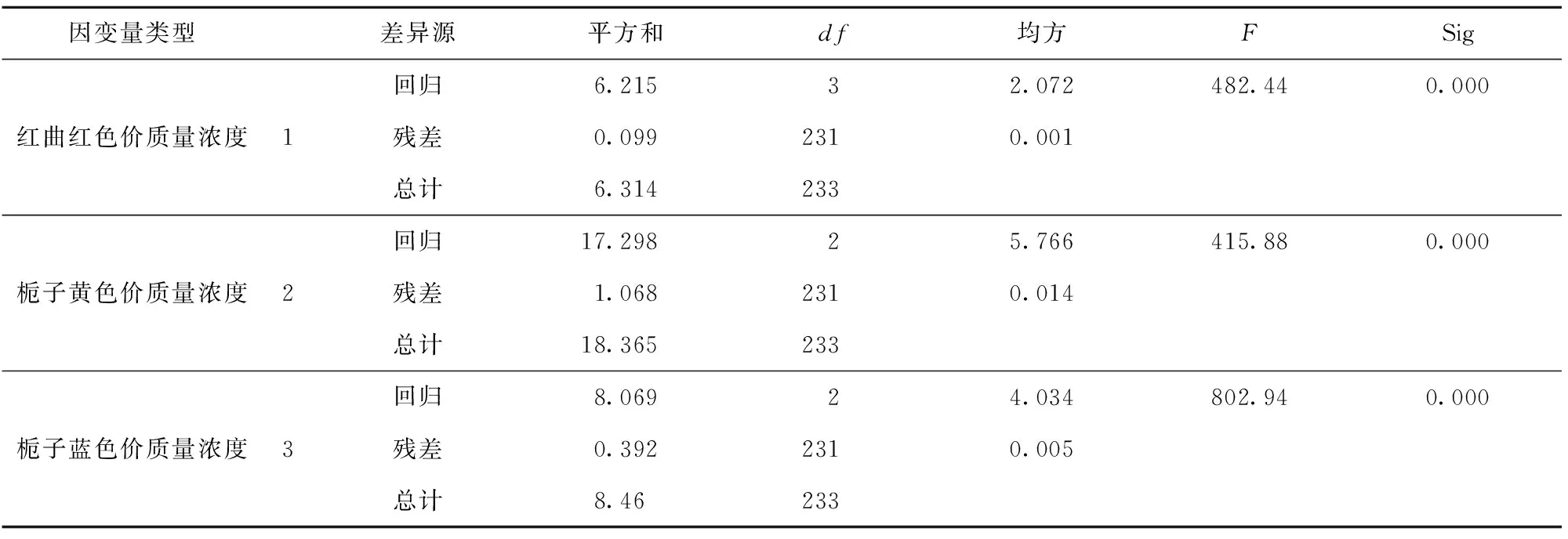
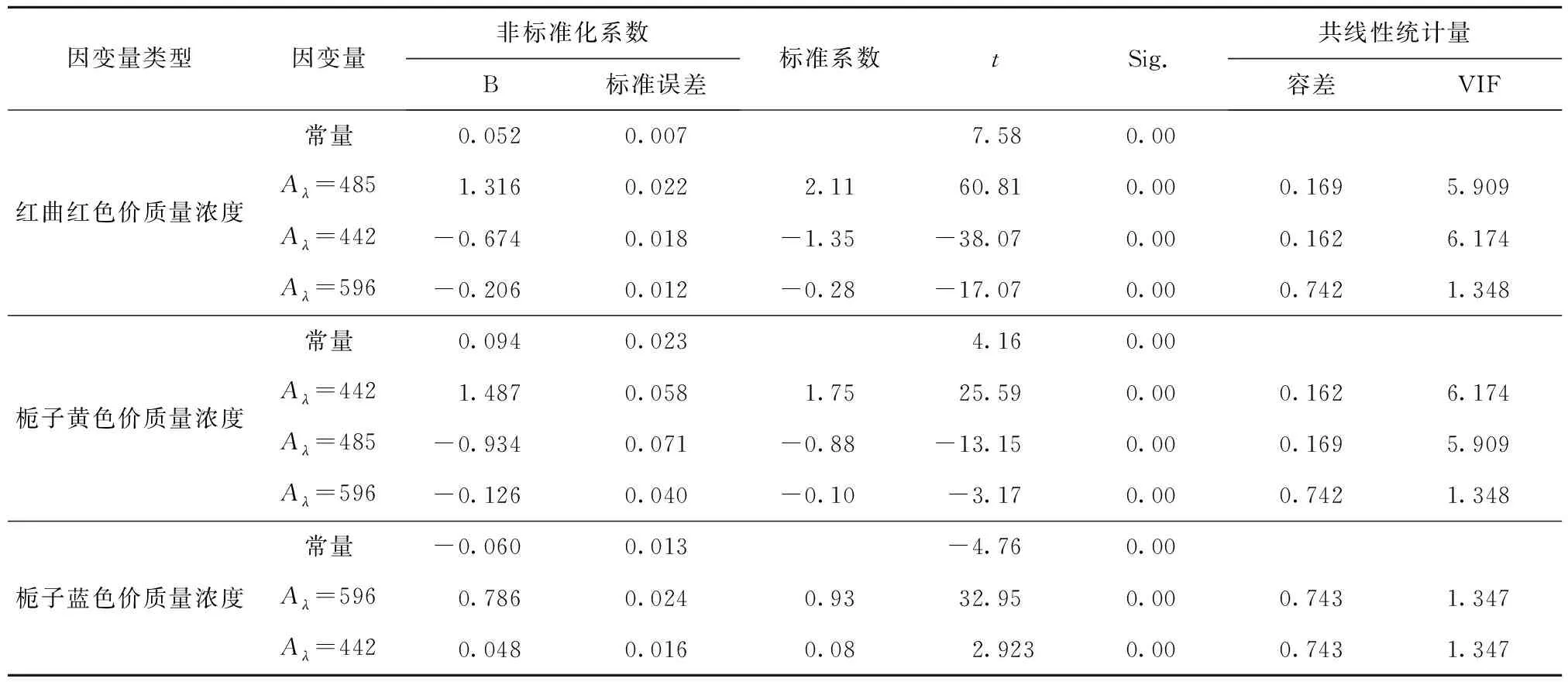
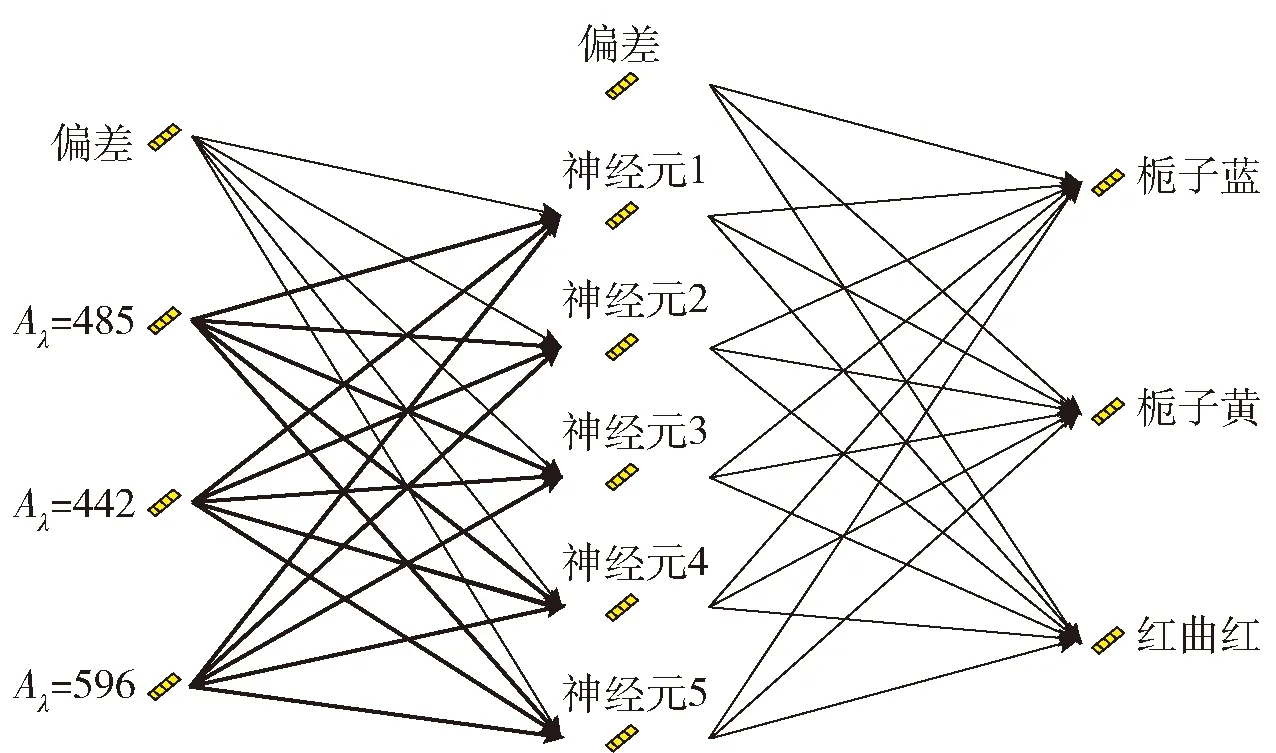
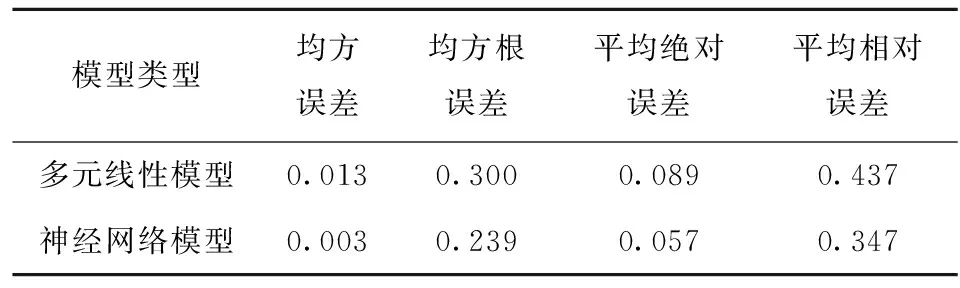
由于不能明确各影响因素对混合色素溶液特征吸收值的影响是否显著,为建立最优回归模型,采用逐步回归方法,对各变量进行F检验,使用F值判定回归模型的变量参数,设置步进方法的F值为:0.05 根据得到的多元线性拟合结果,得到变量移入移除表和模型拟合度检验表(见表2),根据R2判定回归方程的拟合度,优化得到最优拟合方程。由表2中红曲红、栀子黄和栀子蓝色价质量浓度为因变量,得到优化拟合方程的R2分别为0.992、0.971、0.977,调整后的R2为0.984、0.942、0.954,R2满足要求,且较接近1,说明构建的回归方程拟合度良好。这与丁海霞[14]的多元线性回归模型分析织物染色配色结果相一致。 根据前述优化后拟合方程,通过方差分析得到F值和显著性结果(见表3)。以红曲红、栀子黄和栀子蓝色价质量浓度为目标值的回归模型F值分别为482.44、415.88、802.94,P值均为0.000,说明建立的回归拟合模型具有统计学上的显著性,回归效果有效,回归方程拟合良好。SPSS软件模型处理得到的回归系数(见表4),系数的共线性统计量中,模型的容忍度均大于0.1,VIF(方差膨胀系数)均小于10,表明该模型不存在多重共线性。 2.3.2多层前馈BP神经网络模型构建 采用IBM SPSS Modeler构建神经网络模型(见图3),将442、485、596 nm的复配色素溶液吸光度设置为神经网络模型输入层,将红曲红、栀子黄、栀子蓝色价质量浓度为神经网络模型输出层,创建标准模型,选择建立多层感知器的神经网络模型,隐藏层数为1个,隐藏层节点为软件自动计算,以不能进一步降低误差为中止规则,将数据以7∶3分为训练区、测试区。隐含层和输出层的传递函数分别为tanh函数,学习速率取0.05,训练目标为0.001,最大迭代次数为1 000,训练的误差精度为0.05。通过软件的多次迭代计算,最终确定当神经网络模型的隐藏层神经元为5个时,准确度和运行时间较佳,R2为0.957。 表2 多元回归分析模型拟合度检验和变量移入表Tab.2 Fitting degree inspection and variable value of multiple regression analysis model 表3 方差分析Tab.3 Analysis of variance 表4 多元回归系数Tab.4 Coefficients of multiple regression 图3 BP神经网络模型Fig.3 BP neural network model 构建的多元线性回归模型和神经网络模型,对预测验证区的156组数据进行预测红曲红、栀子黄、栀子蓝色素色价质量浓度。根据模型结果,通过计算多元线性模型和神经网络模型的平均绝对误差(MAE)、平均相对误差(MAPE)、均方误差(MSE)和均方根误差(RMSE)等4项指标评价模型的精确度(见表5),表明神经网络模型的各个误差指标均小于多元线性回归拟合模型,说明神经网络模型精度较高,且相比于多元线性回归模型较稳定。因此,采用BP神经网络模型作为天然色素的复配模型,该结果与对橄榄油中二元、三元混合物的拟合结果相一致[20-21]。 表5 模型预测性能对比Tab.5 Comparison of model predictive ability 采用神经网络模型进行复配模型的验证,从样品制备表中随机选择5个色素复配配方,根据获得样品的光谱吸收曲线;通过模型预测计算得到预测配方,使用全自动色差仪分别测量原配方和拟合配方获得的颜色(色调)参数;根据CIELAB色差公式[见式(3)],计算两者的色差(见表6)。由表6可知,根据神经网络模型计算得到预测配方与原配方溶液的平均色差为1.604,肉眼无法分辨两者的差别。 表6 原配方与拟合配方的色差比较Tab.6 Comparison of color aberration between sampleformula and fitting formula 本文分别测定了红曲红、栀子黄和栀子蓝单一色素溶液及3种色素复配溶液的吸收光谱,通过分析吸收光谱发现,复配色素溶液的特征吸收峰与参与复配的单一色素的最大特征吸收峰基本一致,且色素溶液的质量浓度与其吸光度呈正比。根据色素复配溶液的特征吸收峰吸光度及其复配比例,构建了多元线性回归模型和神经网络模型,通过模型误差分析,表明神经网络模型相较于多元线性模型具有更高的精度和稳定性,神经网络模型适用于天然色素复配模型构建。通过试验验证得出,预测配方和原配方溶液的色差在3以内,肉眼无法区分两者的差别,表明使用该配色模型对天然食用色素溶液配色精确度、重复性良好,可以较好地满足实际生产及应用的需要。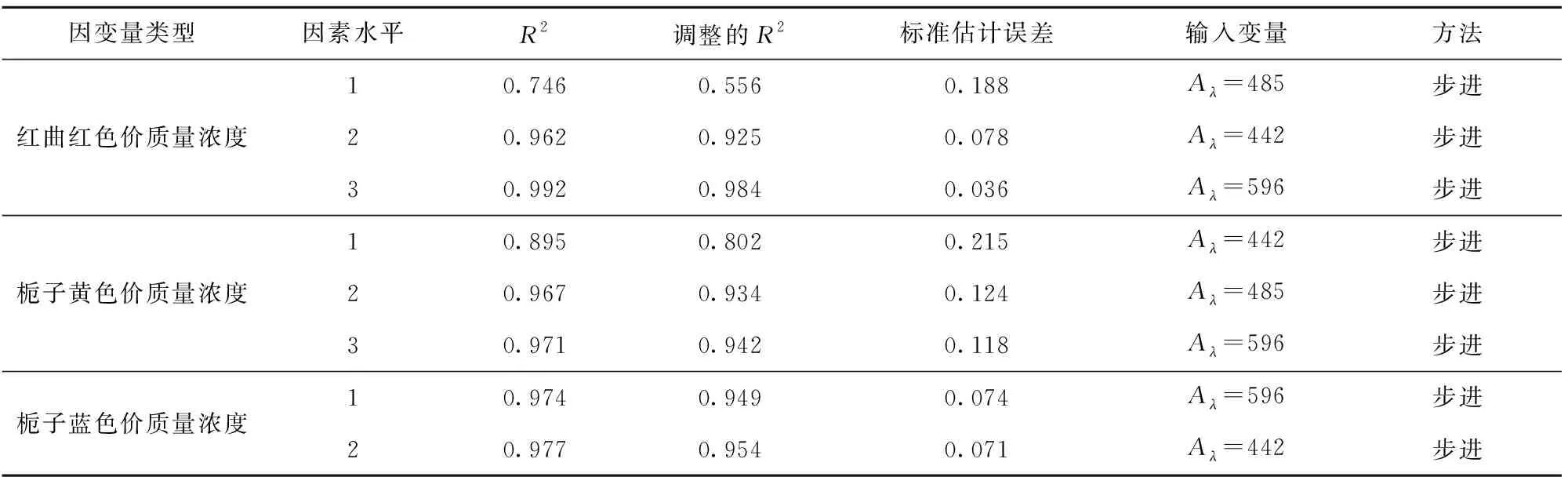
2.4 2种模型的对比分析
2.5 复配模型验证

3 结 论
