基于VR设备中IMU的头部姿态感知算法研究

张雁鹏,高建勇,周志杰

(1.苏州热工研究院有限公司 设备管理部，广东 深圳 518028; 2.华能山东石岛湾核电有限公司 生产管理部，山东 荣成 264312)

0 引言

由于头戴式显示设备(HMD,head-mounted device)的发展，基于虚拟现实(VR,virtual reality)的教育培训随之流行开来[1-4]。由于VR技术具有集成性、交互性等特点，利用VR技术可以创造出一个真实的教学环境，可以方便的模拟课堂环境下不便于布置的一些场景，为教师教学提供了形象直观的表达工具，将信息技术与学科课程的教与学融为一体。而在使用过程中，使用者可以与VR设备播放视频中的对象进行交互，可以像真实场景中随着头部的转动看到不同的景色，达到身临其境的效果。因此，VR设备对使用者头部姿态的感知尤为重要。

为了方便地使用VR头戴式设备，必须满足一些条件：首先，设备在形式上必须是独立的，有自己独立的电源和处理系统； 其次，设备的重量和功耗必须越低越好；最后，设备处理的延迟时间应该越小越好。采用外部视觉跟踪设备对人体头部姿态进行测量的方式[5-6]，需要安装额外的装置，破坏了VR设备使用的独立性，同时极大地增加了使用的成本，且具有场地使用的局限性，同时由于通过外部设备进行姿态处理，存在时间延迟的问题。而使用低成本惯性测量单元(IMU，inertial measurement unit)与头戴式设备固定连接的方式进行姿态测量，可以方便地通过VR设备中的嵌入式系统读取IMU内部的加速度、角速度以及磁场强度数据，进而运行姿态解算程序，在保证可靠精度的同时，降低了使用成本。

在IMU姿态解算中，欧拉角法、四元数法等为常用的依靠陀螺仪数据的姿态解算方法。由于欧拉角法导致的“万向锁”问题，大多数测姿系统多采用四元数法进行姿态更新，而求解四元数更新方程多采用四阶龙格库塔法[7]。龙格库塔法通过在每个子区间的选定点上，用对一阶导数的多次求值，来代替截断泰勒级数中计算高阶导数的方法。而这种常规的方法，将4个微分方程进行多次迭代，描述算法的逻辑简单、精度较高，缺点是计算量大、实时性较差。而计算量所对应的就是整个VR设备的功耗问题。对于使用电池的头戴式VR设备，功耗问题很大程度上影响了用户体验。同时，单纯使用依靠陀螺仪数据的基于四元数更新的姿态解算方法，经过长时间运行后，系统的航向角会发生发散，不利于提供稳定的航向精度，因此需要使用地磁信息进行辅助。

针对准确感知头部姿态和降低解算计算量的问题，本文设计了4种基于头戴式IMU的姿态解算方法，包括单独使用龙格库塔法计算姿态角、龙格库塔法更新四元数加融合地磁的扩展卡尔曼滤波算法、单独使用三阶泰勒法计算姿态角以及使用三阶泰勒法更新四元数加融合地磁的滤波算法四种算法，并设计实验对比了这四种算法的姿态精度和运算效率。

1 姿态感知算法

本文设计了4种基于头戴式IMU的姿态解算方法，包括单独使用龙格库塔法计算姿态角、龙格库塔法更新四元数加融合地磁的扩展卡尔曼滤波算法、单独使用三阶泰勒法计算姿态角以及使用三阶泰勒法更新四元数加融合地磁的滤波算法四种算法。如图1所示，整体框图表示基于扩展卡尔曼滤波器(EKF,extended kalman filter)的姿态感知算法，即龙格库塔法更新四元数加融合地磁的滤波算法和使用三阶泰勒法更新四元数加融合地磁的滤波算法。图中，虚线框部分表示只依靠陀螺仪数据的姿态解算方法。该算法通过不断迭代四元数方程(如式(2)所示)求解姿态四元数，进而可以将四元数通过旋转矩阵换算为3-D姿态角。按照四元数方程求解方法的不同，可以分为龙格库塔法和三阶泰勒展开法，也就是本文中使用的姿态解算方法中的两种。四种算法的具体细节将会在下面的章节中一一解释。

图1 测姿算法整体结构框图

1.1 相关基础知识

刚体在空间中的姿态可以通过四元数进行表示，四元数可以表示为：

q=q0+q1i+q2j+q3k

(1)

其中:q0表示四元数的实部或标量部分，而q1i+q2j+q3k表示虚部或矢量部分。

四元数通过四元数微分方程[8]求得：

(2)

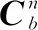
(3)

由四元数和姿态角之间的关系可以将四元数转化为相应的俯仰角θ、滚转角γ、偏航角ψ：

(4)

1.2 四阶龙格库塔法

四阶龙格库塔法是求解四元数微分方程的经典数值积分方法，通过在每个子区间的选定点上，用对一阶导数的多次求值，来代替截断泰勒级数中计算高阶导数的方法，其求解过程可写成以下递推表达式：

(5)

其中：Δt为采样时间，k0、k1、k2、k2为四阶龙格库塔法的系数，其表达式如下:

(6)

1.3 三阶泰勒展开法

根据文献[7]，另一种求解四元数微分方程的方法是对四元数微分方程进行泰勒级数展开，然后取三阶项，可以表示为：

(7)

其中：Δφt+1和Δφt分别为t+1和t时刻的角增量。

1.4 融合地磁的间接扩展卡尔曼滤波方法

EKF是标准卡尔曼滤波在非线性情形下的一种扩展，它是一种高效率的递归滤波器(自回归滤波器)，包含状态方程和测量方程。EKF的基本思想是利用泰勒级数展开将非线性系统模型线性化，然后采用标准卡尔曼滤波框架对信号进行滤波[9]。在本文中，我们没有直接利用EKF对系统的状态量进行估计，而是采用了它的间接形式，即对系统状态量的误差量进行估计。这样做的好处是，由于系统误差量相对于直接状态量属于小值，所以对误差方程的线性化相较于对直接状态方程进行线性化，丢失的信息更少，因此采用间接方式使EKF估计的结果更接近于最优值。

我们利用EKF的间接形式，融合地磁数据，对测姿系统的姿态误差以及陀螺仪零位偏移误差进行最优估计。测姿算法整体结构框图如图1所示。算法的主要流程为：首先，由当前时刻经过零偏补偿后的陀螺仪输出y和前一时刻旋转四元数的后验估计q+通过四元数更新方程(该方程可以通过四阶龙格库塔法或者三阶泰勒展开求解，也就是本文中所提到的龙格库塔法和三阶泰勒展开法)得到当前时刻旋转四元数的先验估计q-；其次，通过计算得到的q-计算当前时刻方向余弦矩阵的先验估计Cnb-；进而，由EKF计算得出的姿态误差向量δφ，然后通过方向余弦更新方程计算出补偿后的方向余弦矩阵Cnb +；最后，计算得出3-D姿态向量φ和下一时刻旋转四元数的后验估计q+用于下一次算法迭代。

1.4.1 系统建模

姿态测量问题可以描述为离散随机系统的估计问题：

xk=f(xk,wk)

zk=h(xk,εk)

(8)

其中:xk∈Rn为k时刻的状态；zk∈Rm为k时刻测量值；f(·)和h(·)分别表示系统的状态方程和测量方程；wk和εk分别表示过程噪声和测量噪声。

系统状态向量xk包含旋转四元数qk和陀螺仪零位偏移bω,k，可以写为：

(9)

只考虑陀螺仪的零偏误差，角速率真值ωk可由陀螺仪输入信号yk获得：

ωk=yk-bω,k+wω,k

(10)

其中:wω,k～N(0,Qω,k)表示陀螺仪的测量噪声。

在本文中，将陀螺仪零位偏移模型表示为一阶马尔科夫模型[6]：

bω,k=bω,k-1+wbω,k

(11)

其中:wbω,k～N(0,Qbω,k)表示陀螺仪的零偏噪声。

EKF通过对当前状态估计的均值进行泰勒展开，从而将非线性系统模型线性化[9]。本文引入EKF的间接形式对姿态测量系统状态向量xk的误差δxk进行估计，进而对xk进行补偿。因为误差四元数δqk为小值，所以姿态误差可以用对应的姿态误差角δφk来表示[10]。因此，系统的误差状态向量将包含6维元素，即:

(12)

其中:δφk表示姿态误差角，δbω,k表示陀螺仪零位偏移误差。

1.4.2 误差状态模型

为了实现滤波器的推导，首先应写出误差的微分方程，然后将其离散化[8]。误差的连续状态方程可以描述为：

(13)

其中:wk～N(0,Qk)为过程噪声向量；Fc,k和Gc,k分别表示连续系统的状态转移矩阵和噪声转移矩阵，具体推导见[11]。

(14)

其中: [ωk×]表示更新后的角速率ωk的斜对称矩阵；I表示单位矩阵；0表示零矩阵。

(15)

离散化后的误差状态方程为：

(16)

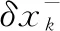
将离散转移矩阵Φk进行一阶泰勒级数展开(相当于将非线性模型线性化)，可得：

Φk=exp(Fc,kΔt)≈I6×6+Fc,kΔt

(17)

其中:Δt表示IMU的采样间隔。

1.4.3 误差测量模型

系统的误差测量模型表示为：

zk=Hδxk+εk

(18)

其中:zk为误差测量向量；H为测量转移矩阵；εk～N(0,Qm,k)为测量噪声的协方差矩阵。

在计算航向角误差前，需要计算地磁航向角。假定三轴磁强计各轴与载体坐标系各轴重合，测量3个轴向的地磁场强度，令磁强计输出为：

(19)

(20)

式中，n系下IMU的滚转角γk、俯仰角θk通过公式(4)求得。

由于地磁北极与地理北极不完全一致，定义地球表面任意点的地磁场强度矢量所在的垂直平面(地磁子午面)与地理子午面的夹角为地磁偏角Bd，不同地区对应有不同的磁偏角。因此地磁航向角可以表示为：

(21)

滤波器的更新方程为：

(22)

2 实验

2.1 实验设置

为了验证本文提出算法的有效性，本文设计了多姿态运动实验。使用的IMU是SBG公司生产的IG-500N，包含三轴加速度计、三轴陀螺仪和三轴磁强计，具体性能指标如表1所示。

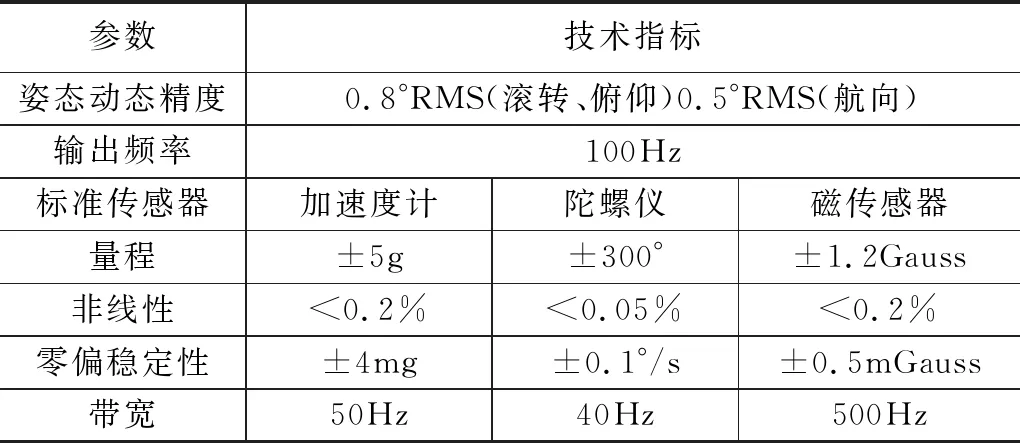
表1 IMU具体性能指标

多姿态运动实验地点为室内直线走廊，实验者将IMU佩戴在头部，依次进行蛇形、俯仰、晃动、转圈和倒退等运动姿态，如图2所示。

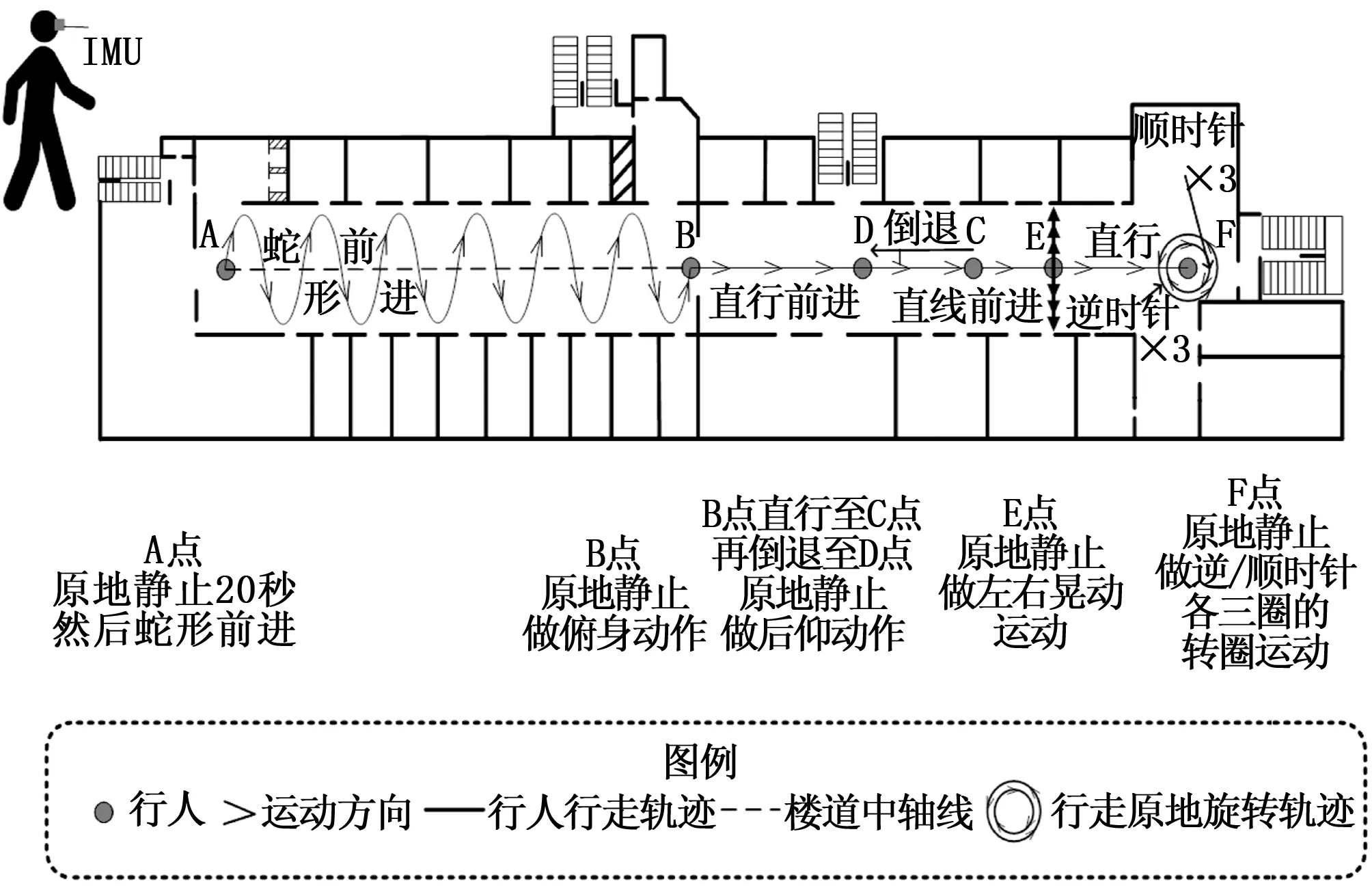
图2 实验环境及实验姿态演示

2.2 实验结果及分析

本文使用Intel i5-540M处理器的笔记本电脑作为硬件平台，使用Matlab R2013a作为软件处理平台。将IMU中自带商业姿态解算软件计算的结果作为基准，计算单独使用龙格库塔法计算姿态角、龙格库塔法更新四元数加融合地磁的扩展卡尔曼滤波算法、单独使用三阶泰勒法计算姿态角和使用三阶泰勒法更新四元数加融合地磁的滤波算法四种算法的解算精度，并列在同一表格中，如表2所示。解算精度由最大偏差值、最小偏差值、平均偏差值和偏差值标准差四项指标来衡量。该四项指标由当前算法的计算结果与基准值差值的绝对值计算得出。同时，为了评估算法的运行效率，给出了计算14 000组数据所需的时间。

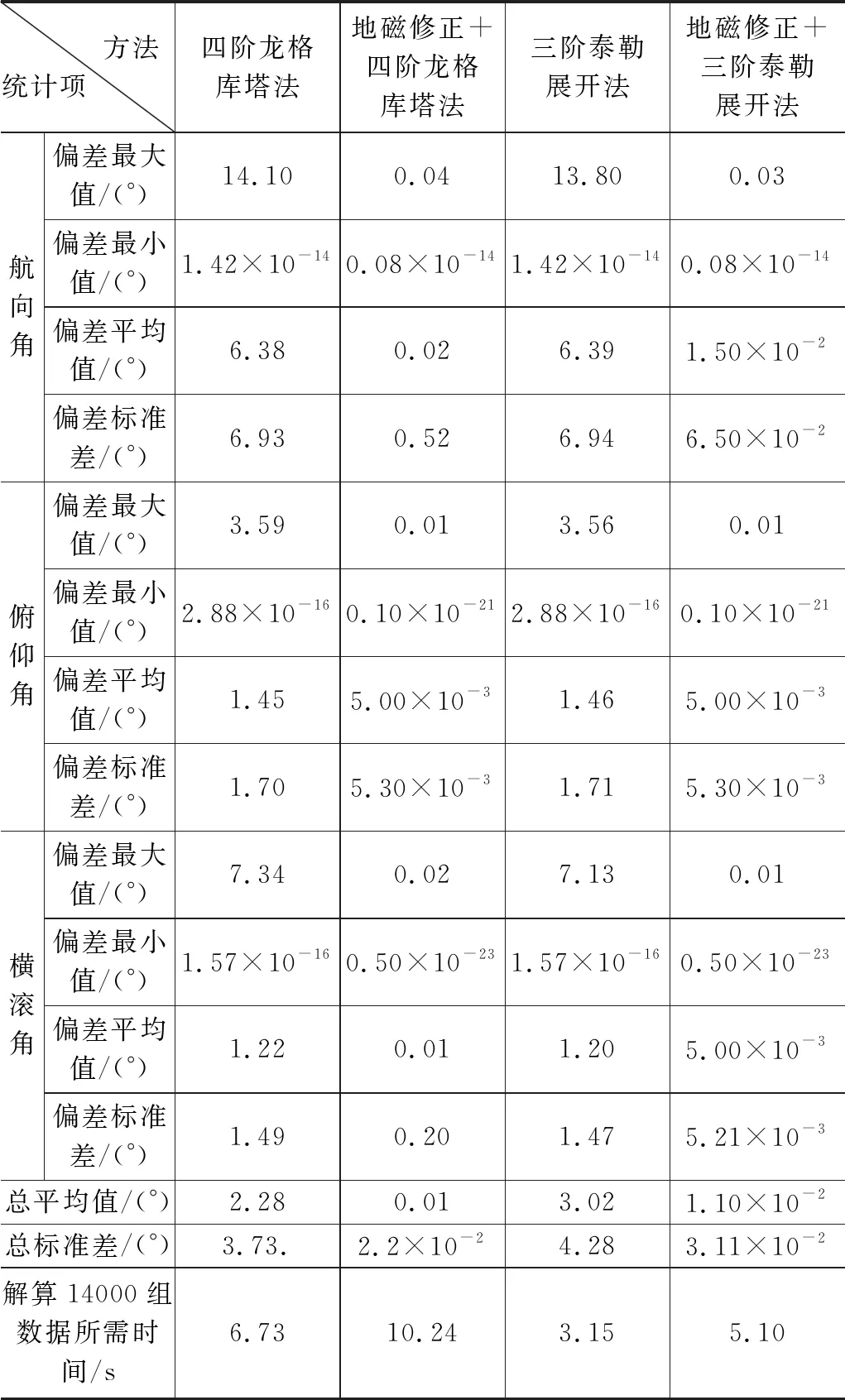
表2 不同算法解算出姿态角的精度

按照算法依赖的传感器数据，将这4种算法分为两组。由于只依赖陀螺仪数据，将四阶龙格库塔法和三阶泰勒展开法划分为第一组，其余依赖陀螺仪和磁强计数据的两种算法划分为第二组。首先，进行组内比较。三阶泰勒展开法相对于四阶龙格库塔法来说，解算精度基本一致，但是三阶泰勒展开法在解算相同数据量的前提下，解算时间明显优于四阶龙格库塔法；三阶泰勒展开法加地磁修正算法和四阶龙格库塔法加地磁修正算法也具有相同的特点。其次，进行组间比较。融合地磁的卡尔曼滤波算法解算精度都要明显优于单独使用两种四元数更新算法，但是解算时间相对较长。由此可得，在保证较高解算精度和较少时间的前提下，三阶泰勒法更新四元数加融合地磁的滤波算法具有更优的性能。

将IMU内部商业姿态解算算法实时输出的姿态角和使用三阶泰勒法更新四元数加融合地磁的滤波算法解算出的姿态角画在同一坐标系中，如图3所示。从图中可以看出，该算法可以有效地解算出人体头部的实际姿态。

图3 多姿态运动解算结果对比

3 结束语

针对头戴式IMU的姿态解算问题，本文设计了4种姿态解算方法，并对比了这4种算法在不同运动状态下的姿态精度。使用三阶泰勒展开法更新四元数，相比于四阶龙格库塔法具有更短的计算时间，同时提出的基于扩展卡尔曼滤波器的姿态测量算法，融合了地磁数据，保证了姿态解算的精度。本文实验结果表明，使用四元数微分方程的三阶泰勒展开递推式更新四元数，同时利用扩展卡尔曼滤波器融合地磁信息进行修正的姿态解算方法，在保证较高解算精度和较少计算时间的前提下，能够有效、稳定的输出高精度姿态数据。但是，本文提出的算法在磁干扰较强的环境中会出现较大的解算误差。在未来的工作中，期望能够找到一种补偿磁干扰环境中姿态解算误差的方法来解决此类问题。